1.4.1 角平分线的性质与判定 基础训练(含答案)
文档属性
| 名称 | 1.4.1 角平分线的性质与判定 基础训练(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
《1.4.1角平分线的性质与判定》
知识点一 角平分线的性质
1.如图,射线OC是∠AOB的平分线,D是射线OC上一点,DP⊥OA于点P,DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( )
A.3
B.4
C.5
D.6
2.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若BD:DC=2:1,BC=7.8 cm,则点D到AB的距离为 .
3.如图,∠C=90°,∠B=30°,AD是△ABC的角平分线.
(1)求证:BD=2CD;
(2)若CD=2,求△ABD的面积.
知识点二 角平分线的判定
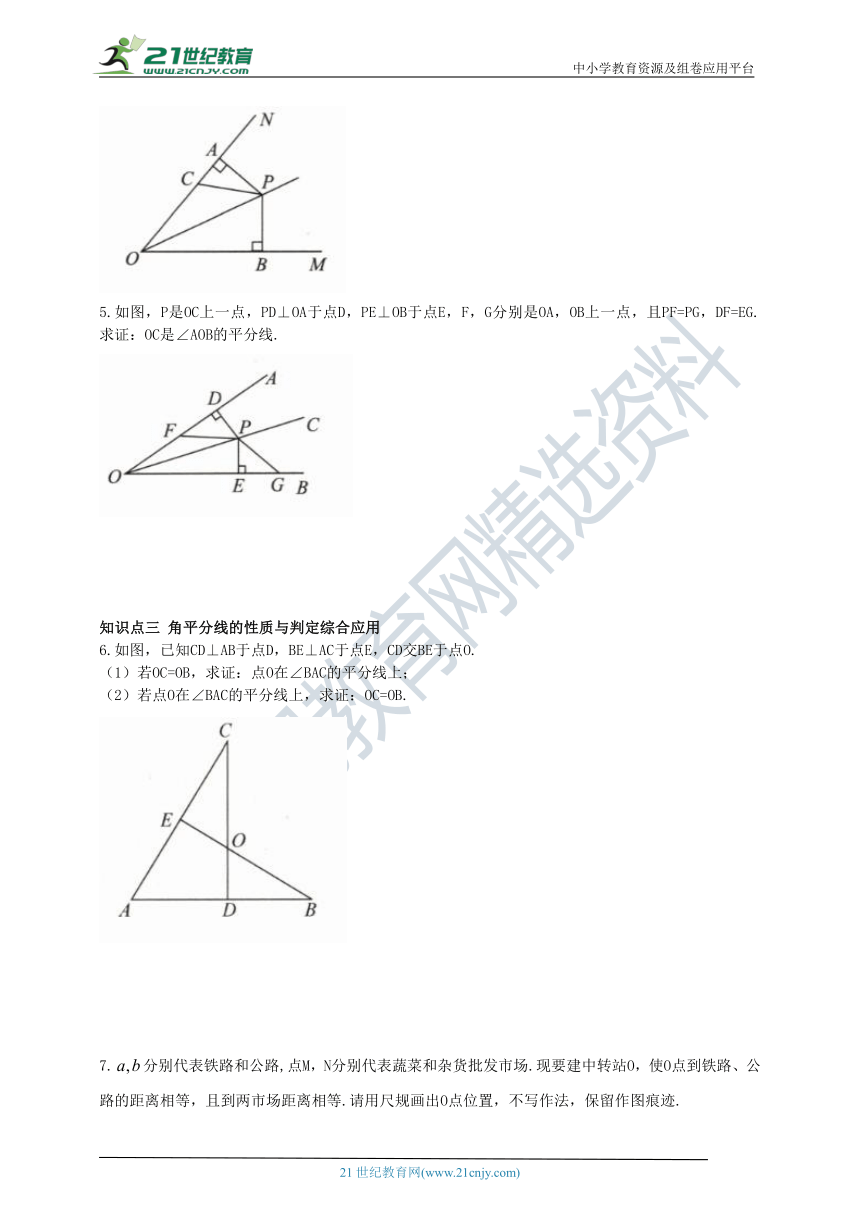
4.如图,PA⊥ON于点A,PB⊥OM于点B,且PA=PB,∠MON=50°,∠OPC=30°,则∠PCA= .
5.如图,P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,F,G分别是OA,OB上一点,且PF=PG,DF=EG.求证:OC是∠AOB的平分线.
知识点三 角平分线的性质与判定综合应用
6.如图,已知CD⊥AB于点D,BE⊥AC于点E,CD交BE于点O.
(1)若OC=OB,求证:点O在∠BAC的平分线上;
(2)若点O在∠BAC的平分线上,求证:OC=OB.
7.分别代表铁路和公路,点M,N分别代表蔬菜和杂货批发市场.现要建中转站O,使O点到铁路、公路的距离相等,且到两市场距离相等.请用尺规画出O点位置,不写作法,保留作图痕迹.
参考答案
1.答案:D
解析:作DE⊥OB于E,如图.
∵OC是∠AOB的平分线,DP⊥OA,DE⊥OB,∴DE=DP=4,∴×3×4=6.故选D.
2.答案:2.6 cm
解析:如图,过点D作DE⊥AB于点E.∵AD平分∠BAC,DE⊥AB,DC⊥AC,∴CD=DE.又∵BD:DC=2:1,BC=7.8 cm,∴DC=7.8÷(2+1)=7.8÷3=2.6(cm),∴DE=DC=2.6 cm.故答案为2.6 cm.
3.答案:(1)【证明】如图,过点D作DE⊥AB于点E.∵∠C=90°,AD是△ABC的角平分线,∴DE=CD.又∵∠B=30°,∴在Rt△BDE中,DE=BD,∴BD=2DE=2CD.
(2)【解】∵∠C=90°,∠B=30°,AD是△ABC的角平分线,∴∠BAD=∠B=30°,∴AD=BD=2CD=4,∴在Rt△ACD中,AC=,∴△ABD的面积为
解析:
4.答案:55°
解析:∵PA⊥ON,PB⊥OM,PA=PB,∴OP平分∠MON.∵∠MON=50°,∴∠POC=25°.∵∠OPC=30∴∠PCA=∠POC+∠OPC=55°.
5.答案:【证明】∵在Rt△PFD和Rt△PGE中,∴Rt△PFD≌Rt△PGE(HL),∴PD=PE. 又∵P是OC上一点,PD⊥OA,PE⊥OB,∴OC是∠AOB的平分线.
解析:
6.答案:【证明】(1)如图,连接AO.∵CD⊥AB,BE⊥AC,∴∠CEB=∠BDO=90°.又∵∠COE=∠BOD,∴∠C=∠B.在△CEO和△BDO中,∴△CEO≌△BDO(ASA),∴OE=OD,∴点O在∠BAC的平分线上.
(2)∵AO平分∠BAC,CD⊥AB,BE⊥AC,∴OD=OE.在△DOB和△EOC中,
∴△DOB≌△EOC(ASA),∴OC=OB.
解析:
7.答案:如图,点O与点O′即为所求.
解析:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
《1.4.1角平分线的性质与判定》
知识点一 角平分线的性质
1.如图,射线OC是∠AOB的平分线,D是射线OC上一点,DP⊥OA于点P,DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( )
A.3
B.4
C.5
D.6
2.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若BD:DC=2:1,BC=7.8 cm,则点D到AB的距离为 .
3.如图,∠C=90°,∠B=30°,AD是△ABC的角平分线.
(1)求证:BD=2CD;
(2)若CD=2,求△ABD的面积.
知识点二 角平分线的判定
4.如图,PA⊥ON于点A,PB⊥OM于点B,且PA=PB,∠MON=50°,∠OPC=30°,则∠PCA= .
5.如图,P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,F,G分别是OA,OB上一点,且PF=PG,DF=EG.求证:OC是∠AOB的平分线.
知识点三 角平分线的性质与判定综合应用
6.如图,已知CD⊥AB于点D,BE⊥AC于点E,CD交BE于点O.
(1)若OC=OB,求证:点O在∠BAC的平分线上;
(2)若点O在∠BAC的平分线上,求证:OC=OB.
7.分别代表铁路和公路,点M,N分别代表蔬菜和杂货批发市场.现要建中转站O,使O点到铁路、公路的距离相等,且到两市场距离相等.请用尺规画出O点位置,不写作法,保留作图痕迹.
参考答案
1.答案:D
解析:作DE⊥OB于E,如图.
∵OC是∠AOB的平分线,DP⊥OA,DE⊥OB,∴DE=DP=4,∴×3×4=6.故选D.
2.答案:2.6 cm
解析:如图,过点D作DE⊥AB于点E.∵AD平分∠BAC,DE⊥AB,DC⊥AC,∴CD=DE.又∵BD:DC=2:1,BC=7.8 cm,∴DC=7.8÷(2+1)=7.8÷3=2.6(cm),∴DE=DC=2.6 cm.故答案为2.6 cm.
3.答案:(1)【证明】如图,过点D作DE⊥AB于点E.∵∠C=90°,AD是△ABC的角平分线,∴DE=CD.又∵∠B=30°,∴在Rt△BDE中,DE=BD,∴BD=2DE=2CD.
(2)【解】∵∠C=90°,∠B=30°,AD是△ABC的角平分线,∴∠BAD=∠B=30°,∴AD=BD=2CD=4,∴在Rt△ACD中,AC=,∴△ABD的面积为
解析:
4.答案:55°
解析:∵PA⊥ON,PB⊥OM,PA=PB,∴OP平分∠MON.∵∠MON=50°,∴∠POC=25°.∵∠OPC=30∴∠PCA=∠POC+∠OPC=55°.
5.答案:【证明】∵在Rt△PFD和Rt△PGE中,∴Rt△PFD≌Rt△PGE(HL),∴PD=PE. 又∵P是OC上一点,PD⊥OA,PE⊥OB,∴OC是∠AOB的平分线.
解析:
6.答案:【证明】(1)如图,连接AO.∵CD⊥AB,BE⊥AC,∴∠CEB=∠BDO=90°.又∵∠COE=∠BOD,∴∠C=∠B.在△CEO和△BDO中,∴△CEO≌△BDO(ASA),∴OE=OD,∴点O在∠BAC的平分线上.
(2)∵AO平分∠BAC,CD⊥AB,BE⊥AC,∴OD=OE.在△DOB和△EOC中,
∴△DOB≌△EOC(ASA),∴OC=OB.
解析:
7.答案:如图,点O与点O′即为所求.
解析:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
