华东师大版七年级数学下册 9.1 三角形 一课一练 (word版含答案)
文档属性
| 名称 | 华东师大版七年级数学下册 9.1 三角形 一课一练 (word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 336.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 07:45:38 | ||
图片预览



文档简介
9.1 三角形习题1
一、选择题
1.三角形的角平分线是( )
A.直线 B.射线 C.线段 D.以上都不对
2.如图,三角形被遮住的两个角不可能是( )
A.一个锐角,一个钝角 B.两个锐角
C.一个锐角,一个直角 D.两个钝角
3.若三角形的一个内角等于另两个内角之差,则这个三角形为( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.任意三角形
4.现有两根长度分别为4cm和6cm的小木棒,请再找一根小木棒,以这三根小木棒为边围成一个三角形.则第三根木棒长X的取值范围是( )
A.25.如图,国旗上的五角星的五个角的度数是相同的,每一个角的度数都是( )
A. B. C. D.
6.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有( )
A.2对 B.3对 C.4对 D.6对
7.锐角三角形的三个内角是∠A、∠B、∠C,如果,,,那么、、这三个角中( )
A.没有锐角 B.有1个锐角 C.有2个锐角 D.有3个锐角
8.如图,一块实验田的形状是三角形(设其为△ABC),管理员从BC边上的一点D出发,沿DC→CA→AB→BD的方向走了一圈回到D处,则管理员从出发到回到原处在途中身体( )
A.转过90° B.转过180° C.转过270° D.转过360°
二、填空题
1.工人师傅在安装木制门框时,为防止变形常常像图中所示,钉上两条
斜拉的木条,这样做的原理是根据三角形的 性.
(
1
3
2
)
2.如图,已知,,那么 .
3.一个三角形的两条高既不在三角形内,又不在三角形外,这个三角形是 .
4.小亮、小丽和小军三位同学同时测量△ABC的三边长.小亮说:“三角形的周长是11”,小丽说:“有一条边长为4”,小军说:“三条边的长度是三个不同的整数” .请你回答,三边的长度应该是 .
5.若为三角形的三边长,此三角形周长为且则 , , .
6.的边上任取一点(异于),连结,可以得到3个不同的三角形(如图(1));在的边上任取两点、(异于),分别连结、,可以得到
个不同的三角形(如图(2));要得到15个不同的三角形,可以在的边上任取 个点(异于),分别与点连结即可.
7.用7根火柴棒首尾顺次连接摆成一个三角形,能摆成不同的三角形的个数为 .
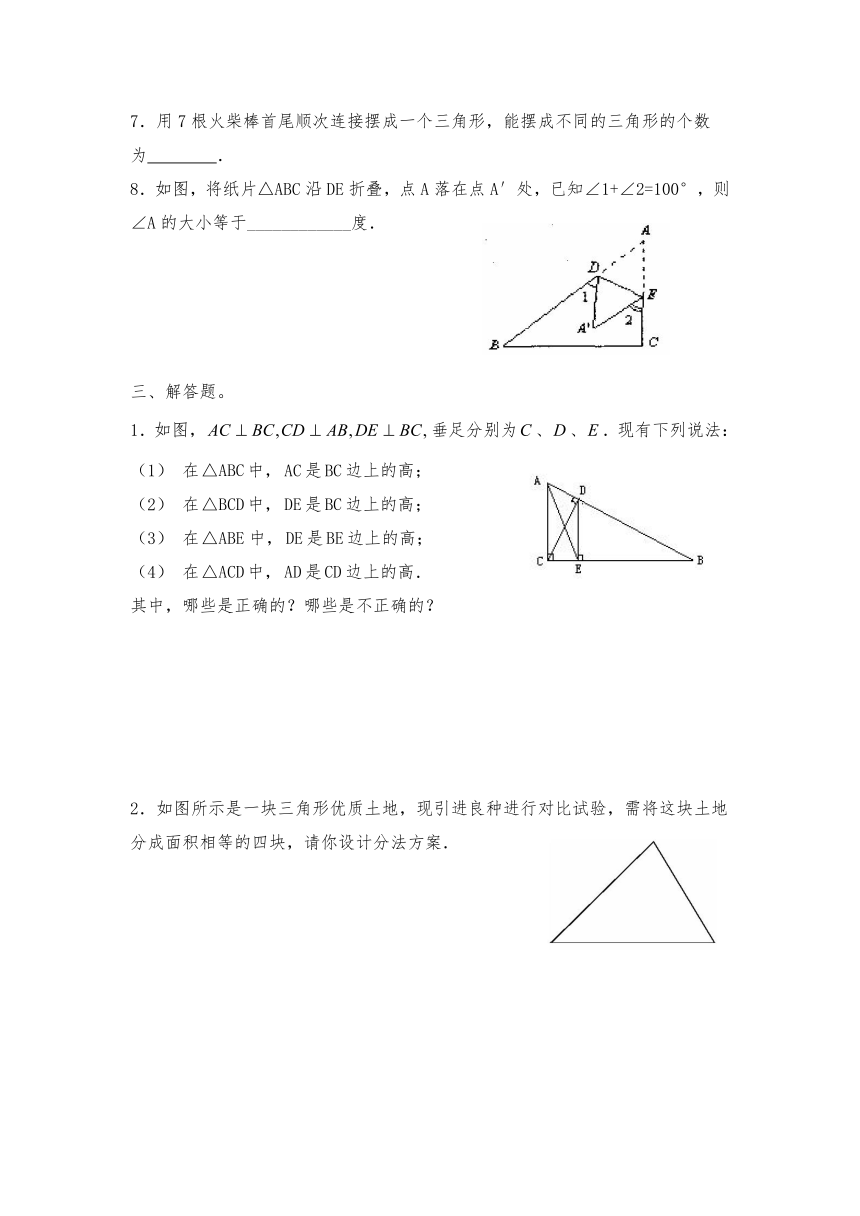
8.如图,将纸片△ABC沿DE折叠,点A落在点A′处,已知∠1+∠2=100°,则∠A的大小等于____________度.
三、解答题。
1.如图,垂足分别为、、.现有下列说法:
在中,是边上的高;
在中,是边上的高;
在中,是边上的高;
在中,是边上的高.
其中,哪些是正确的?哪些是不正确的?
2.如图所示是一块三角形优质土地,现引进良种进行对比试验,需将这块土地分成面积相等的四块,请你设计分法方案.
3.如图,△ABC中,∠B=32°,∠C=55°,AD⊥BC于D, AE平分∠BAC交BC于E,求∠EAD的度数.
4.已知等腰三角形一腰上的中线将三角形的周长分成和两部分,求这个三角形腰长和底边的长.
5.一个零件的形状如图,按规定应等于,和应分别是和.检验工人量得,就断定这个零件不合格.运用三角形的有关知识说明零件不合格的理由.
四、综合提升
1.两条平行直线上各有个点,用这对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当时的情况,此时图中三角形的个数为0;
图2展示了当时的一种情况,此时图中三角形的个数为2;
(1)当时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为 个;
(2)试猜想当对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当时,按上述规则画出的图形中,最少有多少个三角形?
图(1) 图(2) 图(3)
2.如图,中,延长到,和的平分线相交于点,爱动脑筋的晓敏同学在写作业时,发现如下规律:
若,则;
若,则;
若,则;
根据上述规律,若,则______.
请你用数学表达式归纳出与的关系:______.
请你证说明你的结论.
3.探索
在图1至图3中,已知△ABC的面积为a .
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连结
DA.若△ACD的面积为S1,则S1=______(用含a的代数式
表示);
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,
使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则
S2=__________(用含a的代数式表示);
(3)在图2的基础上延长AB到点F,使BF=AB,连结FD,
FE,得到△DEF(如图3).若阴影部分的面积为S3,则
S3=__________(用含a的代数式表示),并运用上述(2)的
结论写出理由.
答案:一、1~8 CDCC CBAD
二、1.稳定 2. 3.直角三角形 4.4,2,5 5.4,8,6
6.6,4 7.2 8.50°
三、1.正确的有:(1)、(2)、(4);
不正确的有:(3).
2.如图所示:
3.因为∠B=32°,∠C=55°,所以∠BAC=180°-32°-55°=93°,
又AE平分∠BAC,所以∠EAC=46.5°,
因为∠DAC=90°-55°=35°,所以∠DAE=46.5°-35°=11.5°
4.解:设等腰三角形腰长为,底边长为,
由题意得或
解得或
第一组解不满足三角形两边之和大于第三边,应舍去
故所求等腰三角形腰长为,底边长为.
5.解:,并延长到.
.
如果零件合格,那么.现量得,所以零件不合格.
四、1.(1)
4
(2)当有对点时,最少可以画个三角形
(3)个
答:当时,最少可以画4010个三角形.
提升能力 挑战自我
2.(4);(5);
(6)∵,
又∵,
∴,
∵,
∴.
3.探索
(1)a ;
(2)2a ;
(3)6a ;
理由:∵CD=BC,AE=CA,BF=AB
∴由(2)得 S△ECD=2a,S△FAE=2a,S△DBF=2a,
∴S3=6a.
一、选择题
1.三角形的角平分线是( )
A.直线 B.射线 C.线段 D.以上都不对
2.如图,三角形被遮住的两个角不可能是( )
A.一个锐角,一个钝角 B.两个锐角
C.一个锐角,一个直角 D.两个钝角
3.若三角形的一个内角等于另两个内角之差,则这个三角形为( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.任意三角形
4.现有两根长度分别为4cm和6cm的小木棒,请再找一根小木棒,以这三根小木棒为边围成一个三角形.则第三根木棒长X的取值范围是( )
A.2
A. B. C. D.
6.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有( )
A.2对 B.3对 C.4对 D.6对
7.锐角三角形的三个内角是∠A、∠B、∠C,如果,,,那么、、这三个角中( )
A.没有锐角 B.有1个锐角 C.有2个锐角 D.有3个锐角
8.如图,一块实验田的形状是三角形(设其为△ABC),管理员从BC边上的一点D出发,沿DC→CA→AB→BD的方向走了一圈回到D处,则管理员从出发到回到原处在途中身体( )
A.转过90° B.转过180° C.转过270° D.转过360°
二、填空题
1.工人师傅在安装木制门框时,为防止变形常常像图中所示,钉上两条
斜拉的木条,这样做的原理是根据三角形的 性.
(
1
3
2
)
2.如图,已知,,那么 .
3.一个三角形的两条高既不在三角形内,又不在三角形外,这个三角形是 .
4.小亮、小丽和小军三位同学同时测量△ABC的三边长.小亮说:“三角形的周长是11”,小丽说:“有一条边长为4”,小军说:“三条边的长度是三个不同的整数” .请你回答,三边的长度应该是 .
5.若为三角形的三边长,此三角形周长为且则 , , .
6.的边上任取一点(异于),连结,可以得到3个不同的三角形(如图(1));在的边上任取两点、(异于),分别连结、,可以得到
个不同的三角形(如图(2));要得到15个不同的三角形,可以在的边上任取 个点(异于),分别与点连结即可.
7.用7根火柴棒首尾顺次连接摆成一个三角形,能摆成不同的三角形的个数为 .
8.如图,将纸片△ABC沿DE折叠,点A落在点A′处,已知∠1+∠2=100°,则∠A的大小等于____________度.
三、解答题。
1.如图,垂足分别为、、.现有下列说法:
在中,是边上的高;
在中,是边上的高;
在中,是边上的高;
在中,是边上的高.
其中,哪些是正确的?哪些是不正确的?
2.如图所示是一块三角形优质土地,现引进良种进行对比试验,需将这块土地分成面积相等的四块,请你设计分法方案.
3.如图,△ABC中,∠B=32°,∠C=55°,AD⊥BC于D, AE平分∠BAC交BC于E,求∠EAD的度数.
4.已知等腰三角形一腰上的中线将三角形的周长分成和两部分,求这个三角形腰长和底边的长.
5.一个零件的形状如图,按规定应等于,和应分别是和.检验工人量得,就断定这个零件不合格.运用三角形的有关知识说明零件不合格的理由.
四、综合提升
1.两条平行直线上各有个点,用这对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当时的情况,此时图中三角形的个数为0;
图2展示了当时的一种情况,此时图中三角形的个数为2;
(1)当时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为 个;
(2)试猜想当对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当时,按上述规则画出的图形中,最少有多少个三角形?
图(1) 图(2) 图(3)
2.如图,中,延长到,和的平分线相交于点,爱动脑筋的晓敏同学在写作业时,发现如下规律:
若,则;
若,则;
若,则;
根据上述规律,若,则______.
请你用数学表达式归纳出与的关系:______.
请你证说明你的结论.
3.探索
在图1至图3中,已知△ABC的面积为a .
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连结
DA.若△ACD的面积为S1,则S1=______(用含a的代数式
表示);
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,
使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则
S2=__________(用含a的代数式表示);
(3)在图2的基础上延长AB到点F,使BF=AB,连结FD,
FE,得到△DEF(如图3).若阴影部分的面积为S3,则
S3=__________(用含a的代数式表示),并运用上述(2)的
结论写出理由.
答案:一、1~8 CDCC CBAD
二、1.稳定 2. 3.直角三角形 4.4,2,5 5.4,8,6
6.6,4 7.2 8.50°
三、1.正确的有:(1)、(2)、(4);
不正确的有:(3).
2.如图所示:
3.因为∠B=32°,∠C=55°,所以∠BAC=180°-32°-55°=93°,
又AE平分∠BAC,所以∠EAC=46.5°,
因为∠DAC=90°-55°=35°,所以∠DAE=46.5°-35°=11.5°
4.解:设等腰三角形腰长为,底边长为,
由题意得或
解得或
第一组解不满足三角形两边之和大于第三边,应舍去
故所求等腰三角形腰长为,底边长为.
5.解:,并延长到.
.
如果零件合格,那么.现量得,所以零件不合格.
四、1.(1)
4
(2)当有对点时,最少可以画个三角形
(3)个
答:当时,最少可以画4010个三角形.
提升能力 挑战自我
2.(4);(5);
(6)∵,
又∵,
∴,
∵,
∴.
3.探索
(1)a ;
(2)2a ;
(3)6a ;
理由:∵CD=BC,AE=CA,BF=AB
∴由(2)得 S△ECD=2a,S△FAE=2a,S△DBF=2a,
∴S3=6a.
