2021-2022学年人教版数学七年级下册5.3.1平行线的性质课后提升(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册5.3.1平行线的性质课后提升(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 385.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 22:59:03 | ||
图片预览



文档简介
平行线的性质
一、单选题
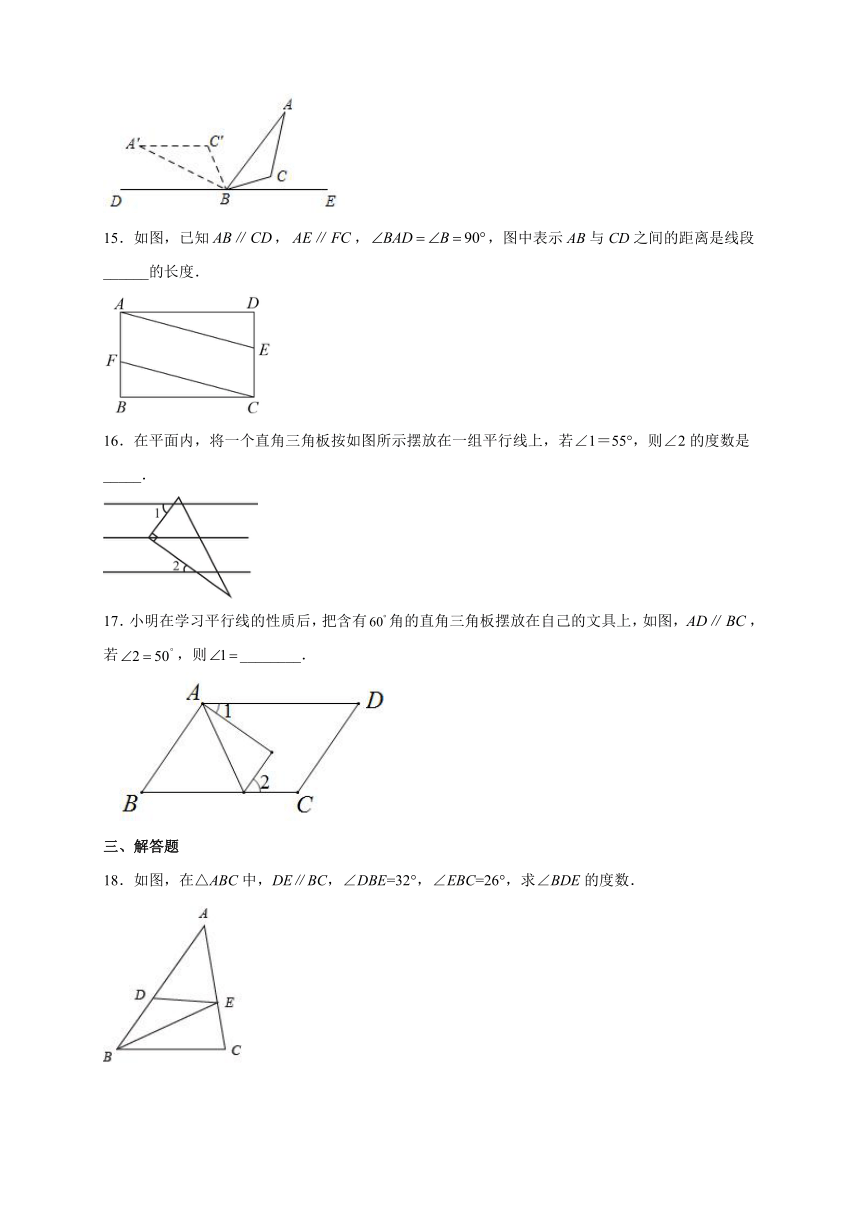
1.如图,若a∥b,∠1=60°27′,则∠2等于( )
A.60°27′ B.60°73′ C.119°33′ D.119°73′
2.如图,四边形ABCD中,ABCD,则下列结论中成立的是( )
A.∠A+∠B=180° B.∠B+∠D=180° C.∠B+∠C=180° D.∠A+∠C=180°
3.将一副直角三角板按如图所示的方式叠放在一起,若AC//DE,则的度数为( )
A.5° B.10° C.15° D.20°
4.如图,将三角板的直角顶点放在直尺的一边上.若,则的度数为( )
A.45° B.50° C.55° D.65°
5.如图,AD//BC,∠DAC=65°,∠ACF=28°,∠EFC=143°,∠B=52°,则∠BEF的度数是( )
A.120° B.125° C.127° D.128°
6.①如图1,ABCD,则∠A+∠E+∠C=180°;②如图2,ABCD,则∠E=∠A+∠C;③如图3,ABCD,则∠A+∠E-∠1=180°;④如图4,ABCD,则∠A=∠C+∠P.以上结论正确的个数是( )
A.①②③④ B.①②③ C.②③④ D.①②④
7.如图,在下列给出的条件中,能判定AB//CD的是( )
A.∠BAD+∠BCD=180° B.∠CDB=∠ABD
C.∠ADB=∠DBC D.∠ABE=∠FAD
8.如图,将直尺与30°角的三角尺叠放在一起,若∠1=50°,则∠2的大小是( )
A.40° B.50° C.70° D.80°
9.如图,AB∥ED,CD∥EF,若∠1=145°,则∠2的度数为( )
A.35° B.40° C.45° D.60°
10.一个学员在广场上驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( )
A.第一次向右拐 50° ,第二次向左拐130° B.第一次向右拐 50° ,第二次向右拐130°
C.第一次向左拐 50° ,第二次向左拐130° D.第一次向左拐 30° ,第二次向右拐 30°
11.直线、、、如图所示.若∠1=∠2,则下列结论错误的是( )
A.ABCD B.∠EFB=∠3 C.∠4=∠5 D.∠3=∠5
12.如果两个角的两边两两互相平行,且一个角的等于另一个角的,则这两个角的度数分别是( )
A.48°,72° B.72°,108°
C.48°,72°或72°,108° D.80°,120°
二、填空题
13.如图,一个合格的变形管道ABCD,需要CD边与AB边平行,若一个拐角∠ABC=110°,则另一个拐角∠BCD=_____时,这个管道符合要求.
14.如图,已知,点在直线DE上,,将绕点逆时针旋转到位置,,若,则______度.
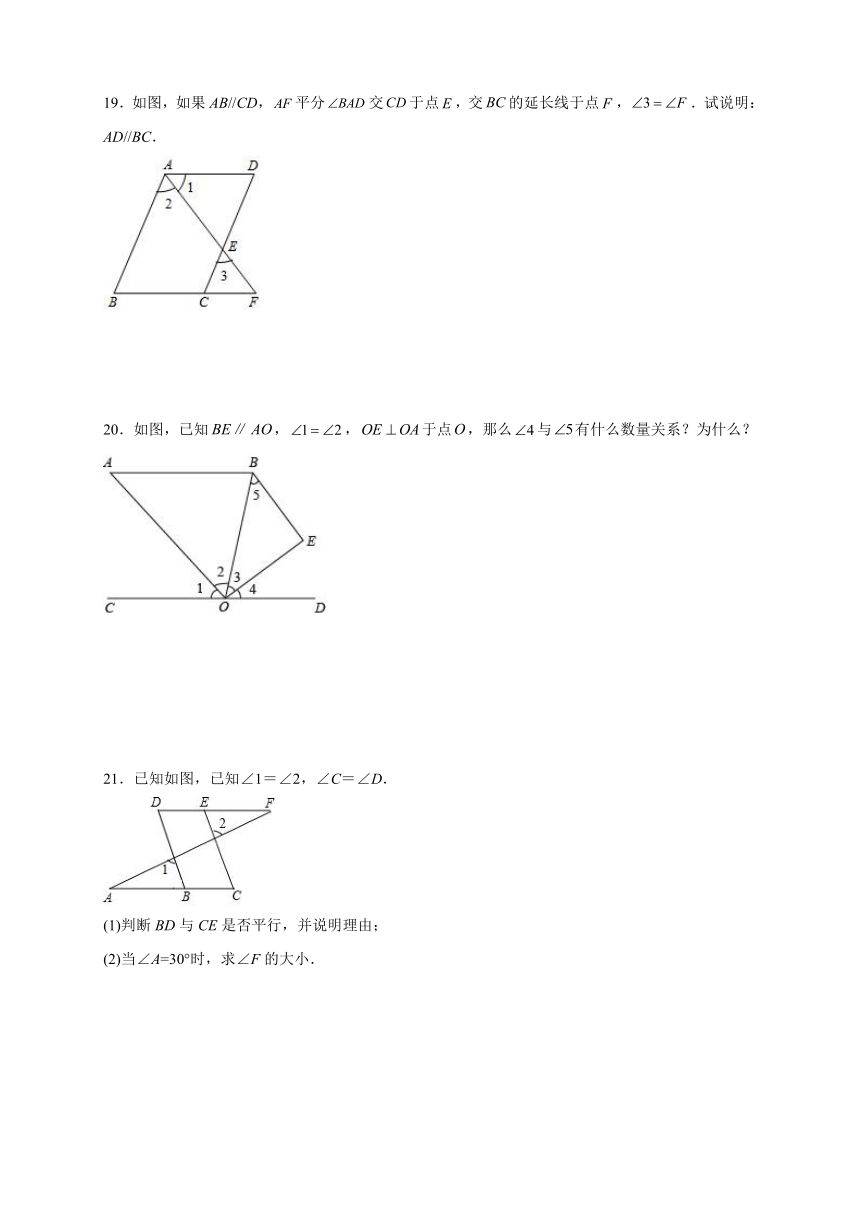
15.如图,已知,,,图中表示AB与CD之间的距离是线段______的长度.
16.在平面内,将一个直角三角板按如图所示摆放在一组平行线上,若∠1=55°,则∠2的度数是_____.
17.小明在学习平行线的性质后,把含有角的直角三角板摆放在自己的文具上,如图,,若,则________.
三、解答题
18.如图,在△ABC中,DE∥BC,∠DBE=32°,∠EBC=26°,求∠BDE的度数.
19.如图,如果AB//CD,平分交于点,交的延长线于点,.试说明:AD//BC.
20.如图,已知,,于点,那么与有什么数量关系?为什么?
21.已知如图,已知∠1=∠2,∠C=∠D.
(1)判断BD与CE是否平行,并说明理由;
(2)当∠A=30°时,求∠F的大小.
22.已知直线l1∥l2,l3和l1,l2分别交于C,D两点,点A,B分别在线l1,l2上,且位于l3的左侧,点P在直线l3上,且不和点C,D重合.
(1)如图1,有一动点P在线段CD之间运动时,求证:∠APB =∠1+∠2;
(2)如图2,当动点P在点C上方运动时,猜想∠APB、∠1、∠2有何数量关系,并说明理由.
试卷第1页,共3页
参考答案:
1.C
解:如图,
由题意得∠3=180°﹣∠1=119°33',
∵a∥b,
∴∠2=∠3=119°33',
故选:C.
2.C
解:∵AB CD,
∴∠A+∠D=180°,∠B+∠C=180°.
只有选项C正确,
故选:C.
3.C
解:由题意可知,,
∵
∴
∵
∴
4.C
解:如图,由题意得:,,
∴.
∵,
∴.
又∵,
∴
故选C.
5.D
解:∵AD//BC,
∴∠ACB=∠DAC=65°,
∵∠ACF=28°,
∴∠FCB=37°,
∴∠EFC+∠FCB=143°+37°=180°,
∴EF//BC.
∵∠B=52°,
∴∠BEF=180°﹣52°=128°.
故选:D.
6.C
解:①过点E作直线,
∵,∴,∴∠A+∠1=180°,∠2+∠C=180°,
∴∠A+∠C+∠AEC=360°,故①错误;
②过点E作直线,
∵,
∴,∴∠A=∠1,∠2=∠C,
∴∠AEC=∠A+∠C,即∠AEC=∠A+∠C,故②正确;
③过点E作直线,
∵,∴,∴∠A+∠3=180°,∠1=∠2,
∴∠A+∠AEC-∠1=180°,即∠A+∠AEC-∠1=180°,故③正确;
④如图,过点P作直线,
∵,∴,
∴∠1=∠FPA,∠C=∠FPC,
∵∠FPA=∠FPC+∠CPA,
∴∠1=∠C+∠CPA,
∵AB∥CD,∴∠A=∠1,即∠A=∠C-∠CPA,故④正确.
综上所述,正确的小题有②③④.
故选:C.
7.B
解:A、当时,不能判定,故不符合题意;
B、当时,由内错角相等,两直线平行可得,故符合题意;
C、当时,由内错角相等,两直线平行可得,故不符合题意;
D、当时,由同位角相等,两直线平行可得,故不符合题意,
故选:B.
8.C
解:∵∠B=30°,∠C=90°
∴∠BAC=90°-∠B =60°,
∵∠1=50° ,∠1+∠BAC +∠BAD=180°
∴∠BAD =180°-∠1-∠BAC=180°-50°-60°=70°
∵EF//AD,
∴∠2=∠BAD=70°
故选:C.
9.A
解:∵AB∥ED,
∴∠1+∠D=180°,
∵∠1=145°,
∴∠D=35°,
∵CD∥EF,
∴∠2=∠D=35°,
故选:A.
10.D
解:∵两次拐弯后,按原来的相反方向前进,
∴两次拐弯的方向相同,形成的角是同位角,
故答案为:D
11.D
解:∵∠1=∠2,
∴AB∥CD,故A正确,不符合题意;
∴∠4=∠5,故C正确,不符合题意;
∵∠EFB与∠3是对顶角,
∴∠EFB=∠3,故B正确,
无法判断∠3=∠5,故D错误,符合题意,
故选:D.
12.B
解:∵两个角的两边两两互相平行,
∴这两个角可能相等或者两个角互补,
∵一个角的等于另一个角的,
∴这两个角互补,
设其中一个角为x,则另一个角为,
根据题意可得:,
解得:,,
故选:B.
13.110°##110度
解:,
,
,
,
故答案为:.
14.55
解:∵,,
∴
∵,
∴
∵由绕点逆时针旋转得到,
∴,
∴,
∵
∴
∴
故答案为:55.
15.BC或AD
解:∵,
∴,
∴(同旁内角互补,两直线平行),
又∵,,
∴,
∴,
∴表示AB与CD之间的距离是线段BC或AD的长度.
故答案为BC或AD
16.35°##35度
解:∵图中的直线互相平行,
∴∠1=∠3,∠2=∠4,
∵∠3+∠4=90°,
∴∠1+∠2=90°,
∵∠1=55°,
∴∠2=90°∠135°,
故答案为:35°.
17.40°
解:∵,,
∴∠1+30°+60°+∠2=180°,
∴∠1=40°,
故答案为:40°.
18.122°
解:∵∠DBE=32°,∠EBC=26°,
∴∠DBC=58°,
∵DE∥BC,
∴∠EDB+∠DBC=180°,
∴∠BDE=180°-58°=122°.
19.见解析
解:∵AF平分∠BAD,
∴∠1=∠2,
∵AB∥CD,
∴∠2=∠3,
∴∠1=∠3,
∵∠3=∠F,
∴∠1=∠F,
∴AD∥BC.
20.∠4与∠5互余,理由见解析
解:∠4与∠5互余,
理由:∵OE⊥OA,
∴∠AOE=90°,即∠2+∠3=90°,
∵∠1+∠2+∠3+∠4=180°,
∴∠1+∠4=90°
∵∠1=∠2,
∴∠2+∠4=90°,
∵,∴∠2=∠5,
∴∠5+∠4=90°,即∠4与∠5互余.
21.(1)平行,理由见解析
(2)30°
解:(1)
BD∥CE,
理由如下:
∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴BD∥CE;
(2)
∵BD∥CE,
∴∠C=∠4,
∵∠C=∠D,
∴∠D=∠4,
∴AC∥DF,
∴∠A=∠F=30°.
22.(1)见解析
(2)∠2=∠1+∠APB.理由见解析
(1)
解:如图①,过点P作PE∥l1,
∵l1∥l2,
∴PE∥l1∥l2,
∴∠1=∠APE,∠2=∠BPE.
又∵∠APB=∠APE+∠BPE,
∴∠APB =∠1+∠2;
(2)
结论:∠2=∠1+∠APB.
证明:如图②,过P作PG∥l1,
∵l1∥l2,
∴PG∥l1∥l2,
∴∠2=∠BPG,∠1=∠APG,
∵∠BPG=∠APG+∠APB,
∴∠2=∠1+∠APB.
答案第1页,共2页
一、单选题
1.如图,若a∥b,∠1=60°27′,则∠2等于( )
A.60°27′ B.60°73′ C.119°33′ D.119°73′
2.如图,四边形ABCD中,ABCD,则下列结论中成立的是( )
A.∠A+∠B=180° B.∠B+∠D=180° C.∠B+∠C=180° D.∠A+∠C=180°
3.将一副直角三角板按如图所示的方式叠放在一起,若AC//DE,则的度数为( )
A.5° B.10° C.15° D.20°
4.如图,将三角板的直角顶点放在直尺的一边上.若,则的度数为( )
A.45° B.50° C.55° D.65°
5.如图,AD//BC,∠DAC=65°,∠ACF=28°,∠EFC=143°,∠B=52°,则∠BEF的度数是( )
A.120° B.125° C.127° D.128°
6.①如图1,ABCD,则∠A+∠E+∠C=180°;②如图2,ABCD,则∠E=∠A+∠C;③如图3,ABCD,则∠A+∠E-∠1=180°;④如图4,ABCD,则∠A=∠C+∠P.以上结论正确的个数是( )
A.①②③④ B.①②③ C.②③④ D.①②④
7.如图,在下列给出的条件中,能判定AB//CD的是( )
A.∠BAD+∠BCD=180° B.∠CDB=∠ABD
C.∠ADB=∠DBC D.∠ABE=∠FAD
8.如图,将直尺与30°角的三角尺叠放在一起,若∠1=50°,则∠2的大小是( )
A.40° B.50° C.70° D.80°
9.如图,AB∥ED,CD∥EF,若∠1=145°,则∠2的度数为( )
A.35° B.40° C.45° D.60°
10.一个学员在广场上驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( )
A.第一次向右拐 50° ,第二次向左拐130° B.第一次向右拐 50° ,第二次向右拐130°
C.第一次向左拐 50° ,第二次向左拐130° D.第一次向左拐 30° ,第二次向右拐 30°
11.直线、、、如图所示.若∠1=∠2,则下列结论错误的是( )
A.ABCD B.∠EFB=∠3 C.∠4=∠5 D.∠3=∠5
12.如果两个角的两边两两互相平行,且一个角的等于另一个角的,则这两个角的度数分别是( )
A.48°,72° B.72°,108°
C.48°,72°或72°,108° D.80°,120°
二、填空题
13.如图,一个合格的变形管道ABCD,需要CD边与AB边平行,若一个拐角∠ABC=110°,则另一个拐角∠BCD=_____时,这个管道符合要求.
14.如图,已知,点在直线DE上,,将绕点逆时针旋转到位置,,若,则______度.
15.如图,已知,,,图中表示AB与CD之间的距离是线段______的长度.
16.在平面内,将一个直角三角板按如图所示摆放在一组平行线上,若∠1=55°,则∠2的度数是_____.
17.小明在学习平行线的性质后,把含有角的直角三角板摆放在自己的文具上,如图,,若,则________.
三、解答题
18.如图,在△ABC中,DE∥BC,∠DBE=32°,∠EBC=26°,求∠BDE的度数.
19.如图,如果AB//CD,平分交于点,交的延长线于点,.试说明:AD//BC.
20.如图,已知,,于点,那么与有什么数量关系?为什么?
21.已知如图,已知∠1=∠2,∠C=∠D.
(1)判断BD与CE是否平行,并说明理由;
(2)当∠A=30°时,求∠F的大小.
22.已知直线l1∥l2,l3和l1,l2分别交于C,D两点,点A,B分别在线l1,l2上,且位于l3的左侧,点P在直线l3上,且不和点C,D重合.
(1)如图1,有一动点P在线段CD之间运动时,求证:∠APB =∠1+∠2;
(2)如图2,当动点P在点C上方运动时,猜想∠APB、∠1、∠2有何数量关系,并说明理由.
试卷第1页,共3页
参考答案:
1.C
解:如图,
由题意得∠3=180°﹣∠1=119°33',
∵a∥b,
∴∠2=∠3=119°33',
故选:C.
2.C
解:∵AB CD,
∴∠A+∠D=180°,∠B+∠C=180°.
只有选项C正确,
故选:C.
3.C
解:由题意可知,,
∵
∴
∵
∴
4.C
解:如图,由题意得:,,
∴.
∵,
∴.
又∵,
∴
故选C.
5.D
解:∵AD//BC,
∴∠ACB=∠DAC=65°,
∵∠ACF=28°,
∴∠FCB=37°,
∴∠EFC+∠FCB=143°+37°=180°,
∴EF//BC.
∵∠B=52°,
∴∠BEF=180°﹣52°=128°.
故选:D.
6.C
解:①过点E作直线,
∵,∴,∴∠A+∠1=180°,∠2+∠C=180°,
∴∠A+∠C+∠AEC=360°,故①错误;
②过点E作直线,
∵,
∴,∴∠A=∠1,∠2=∠C,
∴∠AEC=∠A+∠C,即∠AEC=∠A+∠C,故②正确;
③过点E作直线,
∵,∴,∴∠A+∠3=180°,∠1=∠2,
∴∠A+∠AEC-∠1=180°,即∠A+∠AEC-∠1=180°,故③正确;
④如图,过点P作直线,
∵,∴,
∴∠1=∠FPA,∠C=∠FPC,
∵∠FPA=∠FPC+∠CPA,
∴∠1=∠C+∠CPA,
∵AB∥CD,∴∠A=∠1,即∠A=∠C-∠CPA,故④正确.
综上所述,正确的小题有②③④.
故选:C.
7.B
解:A、当时,不能判定,故不符合题意;
B、当时,由内错角相等,两直线平行可得,故符合题意;
C、当时,由内错角相等,两直线平行可得,故不符合题意;
D、当时,由同位角相等,两直线平行可得,故不符合题意,
故选:B.
8.C
解:∵∠B=30°,∠C=90°
∴∠BAC=90°-∠B =60°,
∵∠1=50° ,∠1+∠BAC +∠BAD=180°
∴∠BAD =180°-∠1-∠BAC=180°-50°-60°=70°
∵EF//AD,
∴∠2=∠BAD=70°
故选:C.
9.A
解:∵AB∥ED,
∴∠1+∠D=180°,
∵∠1=145°,
∴∠D=35°,
∵CD∥EF,
∴∠2=∠D=35°,
故选:A.
10.D
解:∵两次拐弯后,按原来的相反方向前进,
∴两次拐弯的方向相同,形成的角是同位角,
故答案为:D
11.D
解:∵∠1=∠2,
∴AB∥CD,故A正确,不符合题意;
∴∠4=∠5,故C正确,不符合题意;
∵∠EFB与∠3是对顶角,
∴∠EFB=∠3,故B正确,
无法判断∠3=∠5,故D错误,符合题意,
故选:D.
12.B
解:∵两个角的两边两两互相平行,
∴这两个角可能相等或者两个角互补,
∵一个角的等于另一个角的,
∴这两个角互补,
设其中一个角为x,则另一个角为,
根据题意可得:,
解得:,,
故选:B.
13.110°##110度
解:,
,
,
,
故答案为:.
14.55
解:∵,,
∴
∵,
∴
∵由绕点逆时针旋转得到,
∴,
∴,
∵
∴
∴
故答案为:55.
15.BC或AD
解:∵,
∴,
∴(同旁内角互补,两直线平行),
又∵,,
∴,
∴,
∴表示AB与CD之间的距离是线段BC或AD的长度.
故答案为BC或AD
16.35°##35度
解:∵图中的直线互相平行,
∴∠1=∠3,∠2=∠4,
∵∠3+∠4=90°,
∴∠1+∠2=90°,
∵∠1=55°,
∴∠2=90°∠135°,
故答案为:35°.
17.40°
解:∵,,
∴∠1+30°+60°+∠2=180°,
∴∠1=40°,
故答案为:40°.
18.122°
解:∵∠DBE=32°,∠EBC=26°,
∴∠DBC=58°,
∵DE∥BC,
∴∠EDB+∠DBC=180°,
∴∠BDE=180°-58°=122°.
19.见解析
解:∵AF平分∠BAD,
∴∠1=∠2,
∵AB∥CD,
∴∠2=∠3,
∴∠1=∠3,
∵∠3=∠F,
∴∠1=∠F,
∴AD∥BC.
20.∠4与∠5互余,理由见解析
解:∠4与∠5互余,
理由:∵OE⊥OA,
∴∠AOE=90°,即∠2+∠3=90°,
∵∠1+∠2+∠3+∠4=180°,
∴∠1+∠4=90°
∵∠1=∠2,
∴∠2+∠4=90°,
∵,∴∠2=∠5,
∴∠5+∠4=90°,即∠4与∠5互余.
21.(1)平行,理由见解析
(2)30°
解:(1)
BD∥CE,
理由如下:
∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴BD∥CE;
(2)
∵BD∥CE,
∴∠C=∠4,
∵∠C=∠D,
∴∠D=∠4,
∴AC∥DF,
∴∠A=∠F=30°.
22.(1)见解析
(2)∠2=∠1+∠APB.理由见解析
(1)
解:如图①,过点P作PE∥l1,
∵l1∥l2,
∴PE∥l1∥l2,
∴∠1=∠APE,∠2=∠BPE.
又∵∠APB=∠APE+∠BPE,
∴∠APB =∠1+∠2;
(2)
结论:∠2=∠1+∠APB.
证明:如图②,过P作PG∥l1,
∵l1∥l2,
∴PG∥l1∥l2,
∴∠2=∠BPG,∠1=∠APG,
∵∠BPG=∠APG+∠APB,
∴∠2=∠1+∠APB.
答案第1页,共2页
