4.3角
图片预览




文档简介
课件84张PPT。4.3.1 角4.3 角4.3.2 角的比较与运算4.3.3 余角与补角4.3.1 角赠言书山有路勤为径
学海无涯苦作舟学习目标1.通过丰富的实例,理解角的形成,建立几何中角的概念。
2.掌握角的两种定义形式和四种表示方法。
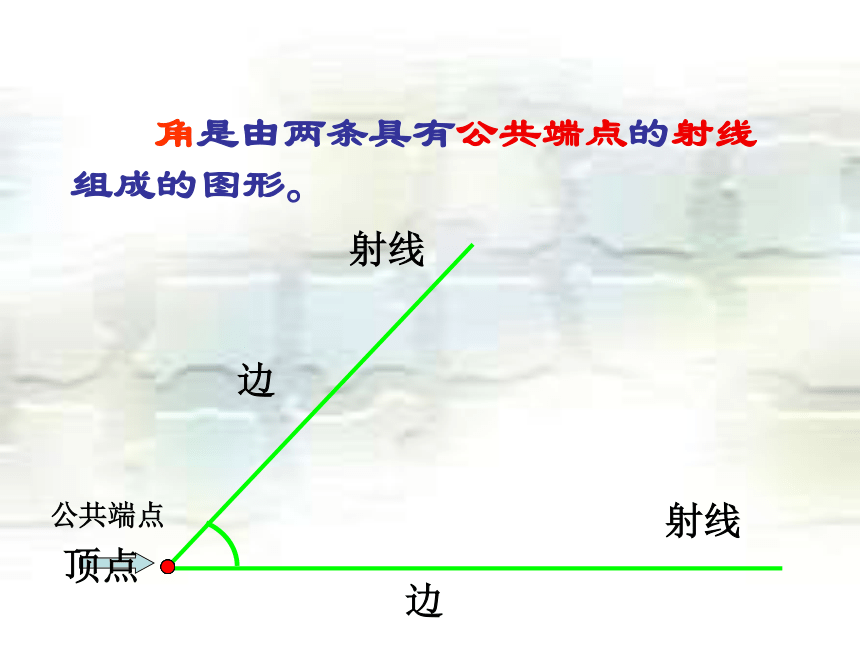
3.结合实际例子,理解平角、周角的概念。 角是由两条具有公共端点的射线
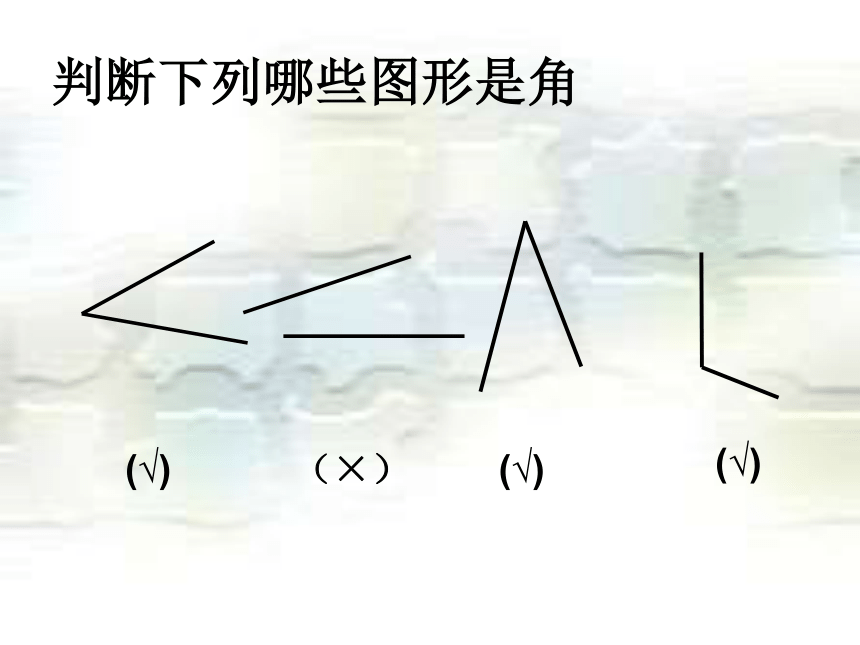
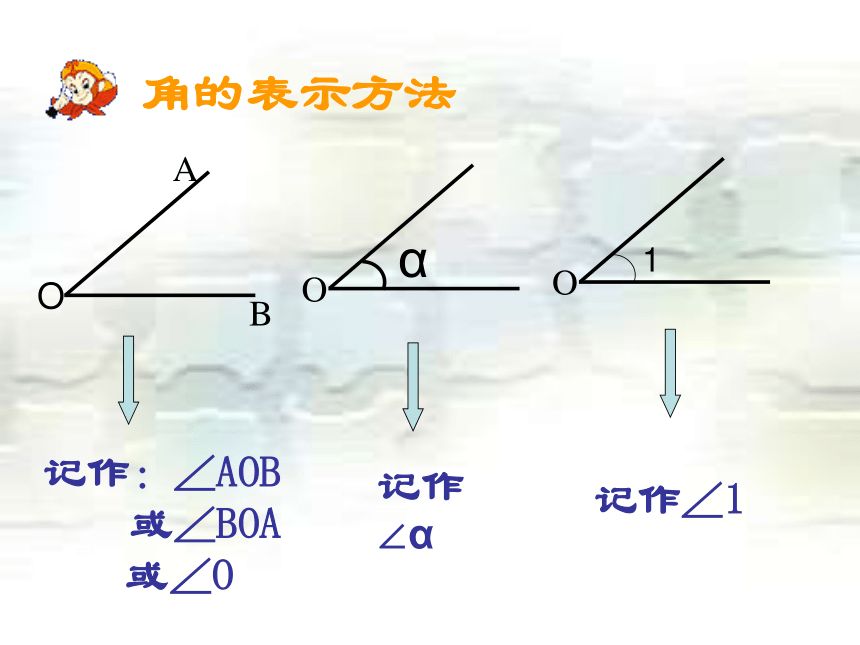
组成的图形。公共端点顶点射线射线边边判断下列哪些图形是角 (√)(√)(√)(×)角的表示方法O1记作:∠AOB 或∠BOA
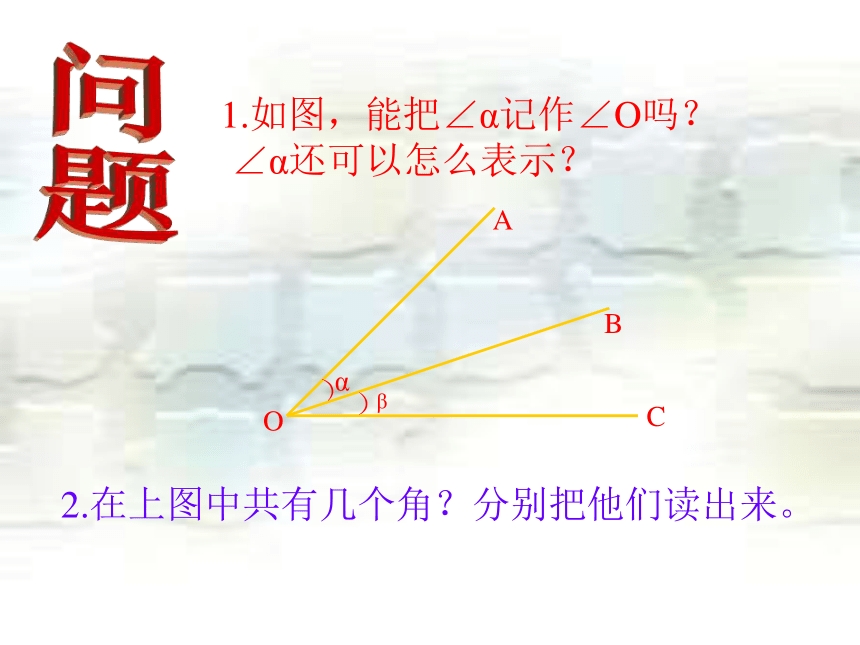
或∠O记作∠α记作∠1问题1.如图,能把∠α记作∠O吗?
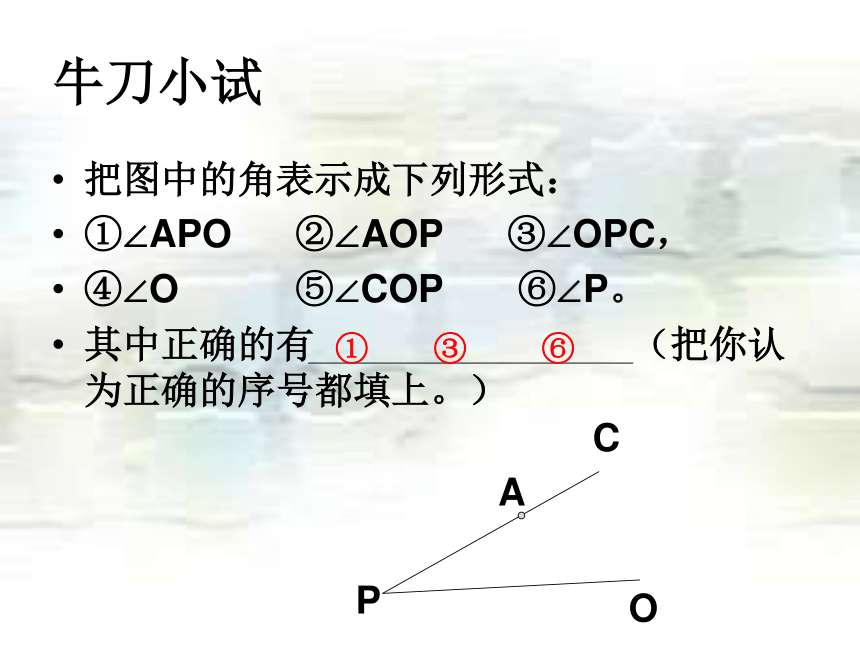
∠α还可以怎么表示?AOCBα))β2.在上图中共有几个角?分别把他们读出来。牛刀小试把图中的角表示成下列形式:
①∠APO ②∠AOP ③∠OPC,
④∠O ⑤∠COP ⑥∠P。
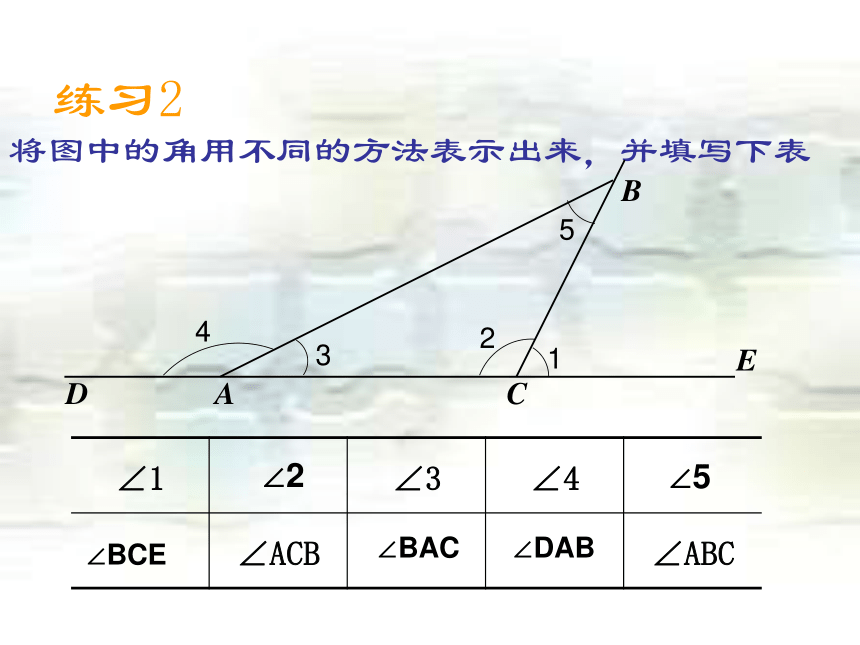
其中正确的有 (把你认为正确的序号都填上。)① ③ ⑥将图中的角用不同的方法表示出来,并填写下表练习2∠BCE∠2
∠BAC∠DAB∠5
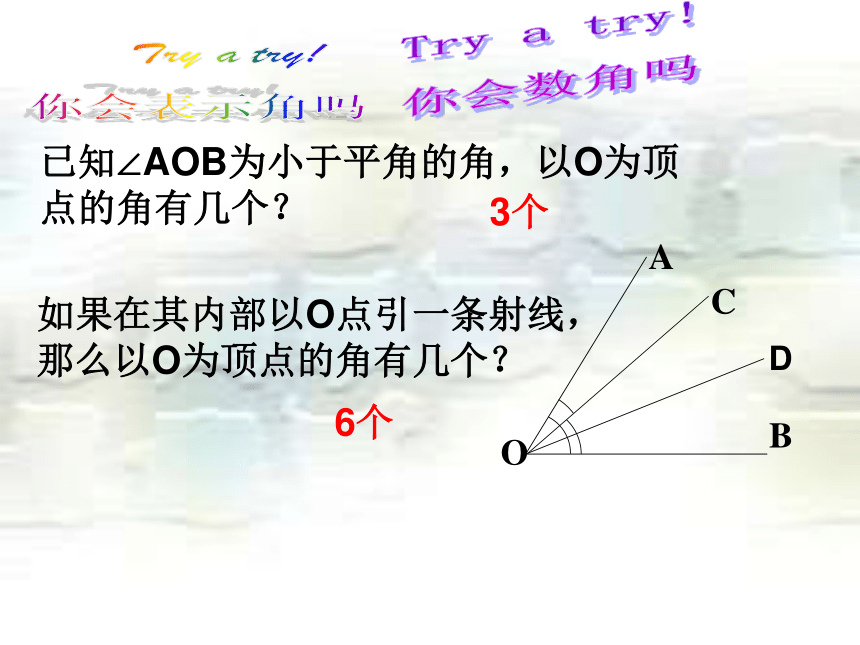
Try a try!
你会表示角吗BCAO已知∠AOB为小于平角的角,以O为顶点的角有几个?3个如果在其内部以O点引一条射线,那么以O为顶点的角有几个?D6个Try a try!
你会数角吗3.如图,以O为顶点的角有几个,请分别把他们
读出来。OABCDE解:共有10个角,
分别是:
∠AOB,∠AOC,
∠AOD,∠AOE,
∠BOC,∠BOD,
∠BOE,∠COD,
∠COE,∠DOE。角也可以看做一条射线绕端点旋转所组成的图形。OBAC 射线OA绕点O旋转,当终点位置OC和起始位置OA
成一直线时,所成的角叫做平角;继续旋转,回到起始
位置OA时,所成的角叫做周角。
平角和周角·始边终边···OAB··OA(B)·顶点说明: 在不做特别说明的情况下,我们说的角都指不大于平角的角如图,棱锥表面上有几个角,请把它们表示出来?练一练 ∠ BAC ∠CAD ∠BAD
∠ABC ∠ABD ∠CBD
∠ACB ∠ACD ∠BCD
∠ ADB ∠ADC ∠BDC考考你选择题:
1.下列语句正确的是( )
A.两条直线相交,组成的图形叫做角
B.两条有公共端点的线段组成的图形叫角
C.两条有公共点的射线组成的图形叫角
D.从同一点引出的两条射线组成的图形叫角
2.下列说法正确的是( )
A.平角是一条直线
B.一条射线是一个周角
C.两条射线组成的图形叫做角
D.两边成一直线的角是平角DD3.判断题
(1)直线是一个平角 ( )
(2)如图(1),点P不在∠AOB的内部 ( )AOB·PABC··DE(3)如图(2), ∠ABC与∠DBE是同一个角( )×× √小结1.角的定义一:
有公共端点的两条射线组成的图形
叫做角,这个公共端点叫做角的顶点,这
两条射线叫做角的边。2.角的定义二:
角可以看成是一条射线绕着它的
端点从一个位置旋转到另一个位置所形成
的图形。射线旋转时经过的平面部分叫角
的内部。3.角的四种表示方法表示方法注意事项1、用三个大写的字母表示表示顶点的字母要写在中间2、用一个顶点的字母来表示一个字母只表示一个角3、用一个数字在靠近顶点的处画上弧线,
并写上数字4、希腊字母表示在靠近顶点的处画上弧线,
并写上希腊字母4.平角、周角的概念创新与应用1.一天24小时中,时钟的时针与分针共组成
多少次平角?多少次周角?
2.某火车站的钟楼上装有一电子报时钟,在
钟面的边界上,每分钟的刻度处都装有一只
小彩灯。晚上九时三十五分二十秒时,时针与分针所夹的角α内装有多少只小彩灯。3.画直线AB,在AB上任取一点O,画射线OC、OD, 这时图中共有几个小于平角的角?分别用三个大写字母表示出来。4.3.2 角的比较与运算记得怎么样比较两条线段的长短方法?即用刻度尺测量线段的
即将其中一条线段移到
3、重叠比较法2、度量法1、观察法 长度的方法。
另一条上作比较。思 考如何比较下列两个角的大小?锐角:00<∠β<900钝角:900< ∠α<1800 1周角>1平角>钝角>1直角>锐角1平角=18001直角=9001周角=3600一:观察法1.将两个角的顶点及一边重合
2. 两个角的另一边落在重合一边的同侧3.由两个角的另一边的位置确定两个角的大小二. 叠合法∠DCE>∠AOB∠DCE<∠AOB∠ DCE =∠AOB三. 度量法1、对“中”—角的顶点对量角器的中心3、读数—读出角的另一边所对的度数2、重合—角的一边与量角器的00刻度
线重合BCA700∠ABC > ∠DEF300比较两个角的大小的方法有三种:观察法
叠合法
度量法小结:两个角的大小关系有三种,记作:
(1) ∠ABC > ∠DEF(2)∠ABC< ∠DEF (3)∠ABC = ∠DEF(E)(F)(E)(F)
A(E)(D)(F)BC 估计图中∠1与∠2的大小关系,
(1)(2)
练习:
并用适当的方法检验.返回下一张上一张退出观察与思考角的大小与角的两边画出的长短有关吗?(1)角的大小与角的两边画出的长短没有关系。
(2)角张开的程度越小,角度就越小结论:迷人数学世界 用放大镜看蚂蚁,用放大镜看自己的手,用放大镜看精致的邮票,用放大镜从太阳光里取火等 等,都会得到令人开心的结果。那么,有没有放大镜放不大的事物呢?你知道放大镜不能“放大”角
的度数的原因吗?
用放大镜来看角因为∠ABC = 700 ,∠DEF=300,
所以∠ABC —∠DEF
=700—300
=400
所以∠ABC — ∠DEF
=∠ABD
三. 角的和与差
700300∠2= ∠1+∠3∠3= ∠2- ∠1∠1= ∠2-∠3三. 角的和差3⌒观 察如图,∠AOC是 ∠AOB与 ∠BOC的和∠AOB是∠AOC与∠BOC的差记作:∠AOC= ∠AOB+ ∠BOC记作:∠AOB=∠AOC—∠BOC类似有∠BOC= ∠AOC—∠AOB图中共有几个角?它们之间有什么关系?
练习2, 如图:∠ AOC = ( ) + ( )
= ( ) - ( ) ∠ BOC=( ) - ( )
= ( ) - ( )∠ AOB∠ BOC∠ AOD∠ COD∠ COD∠ BOD∠ AOC∠ AOB 如图∠ AOB= ∠ COD=900,
∠ AOD=1460, ∠ BOC= ;340D练习3 图中∠1= ∠2, 试判断∠BAD和∠EAC的大小, 并说明理由.冲击解: ∠BAD= ∠2+ ∠DCA
∠EAC= ∠1+∠DCA
探究: 借助一个三角尺可以画出哪些度数的角,用一副三角尺你还能画出哪些度数的角?上台来展示你的结果。75°15°105 °15°120°小结:1、角的大小比较方法:4、三角板可拼出哪些角? 3、角的和差计算 2、角的大小关系有哪些?
动手动脑数一数:图中共有几个小于平角的角,找出规律。(1)(2)123OABCDEFOABCDE(3)(4)……
如果以o为端点,有n条射线,那么组
成的角有多少个?共有(n-1)+(n-2)+(n-3)+…+3+2+1=n(n-1)/2
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线。∵OB平分∠AOC
∴ ∠AOB= ∠BOC= ∠AOC
∠AOC=2 ∠AOB=2 ∠BOC角的三等分线探究1:利用折纸作角平线探究2:利用量角器作角平分线∠AOB=70o70o÷2=35o例题1:已知∠AOB=90o, ∠BOC=30o,OE平分∠AOB,OF平分∠BOC,求∠EOF的度数。解:∵OE平分∠ AOB
∴ ∠EOB= ∠AOB=45o∵OF平分∠ BOC
∴ ∠BOF= ∠BOC=15o∠EOF= ∠EOB+ ∠BOF=45o+15o=60o例题2:如图, ∠AOC=62o, ∠BOD=100o,OE平分∠BOD,OB平分∠AOC,求∠BOE、 ∠COE、 ∠AOE的度数。1.如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55o,则∠BOD的度数是( )
A.35o B.55o
C.70o D.110o2.若将一个平角三等分,则两旁两个角的平分线组成的角是( )
A.90o B.120o C.100o D.105o
3.如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=25o,则∠AOB等于( )
A.50oB.70oC.20oD.100o4.如图1, ∠COD=116o, ∠BOD=90o,OA平分∠BOC,求∠AOB的度数.
5.如图2,已知直线AB,CD相交于点O,OA平分∠EOC, ∠EOC=70o,求∠BOD的度数.角度的换算一周角=2平角=4直角=3600
一平角=1800
一直角=900
10=60/ 1/=60//
(读成1度等于60分,1分等于60秒 )
请你要牢记哟!例题 1 填空
(1)34.50= 0 /
(2)112.270= 0 / //
解:(1)34.50=340+0.50
=340+0.5×60/
=340+3 0/=34030/
(2)112.270=1120+0.27×60/
=1120+16.2/
=1120+16/+0.2×60//
=112016/12//3430112161210=60/
1/=60//例题2 把下列各题结果化成度
72036/ (2)37014/24//
解:(1)72036/=720+36/
=720+(36÷60)0
=720+0.60
=72.60
(2)37014/24//=370+14/+24//
=370+14/+(24÷60)/
=370+14/+0.4/
=370+14.4/
=370+(14.4÷60)0
=370+0.240=37.240例题3 计算(1) 12036/56// + 45024/35//
解:(1)原式=(12+45)0+(36+24)/+(56+35)//
=570+60/+91//
=570+61/+31//
=580+1/+31//
=5801/31//这里的加与减,要将度与度、分与分、秒与秒分别相加时逢60进位,相减时要借1作60.(2) 79045/ - 61048/49//
解:原式=79044/60//- 61048/49//
=780104/60// - 61048/49//
=(78 -61)0 + (104 -48)/ + (60-49)//
=17056/11//
(3)21031/27//×3
解:原式=(21×3)0+ (31×3)/+ (27×3)//
=63093/81//
=63094/21//
=64034/21//(4) 63021/39//÷3
解:原式=(63÷3)0+ (21÷3)/+ (39÷3)//
=2107/13//
(5)10606/25//÷5
解:原式=(106÷5)0+ (6÷5)/+ (25÷5)//
=210+ (66÷5)/ + (25÷5)//
=210+13/+ (85÷5)//
=21013/17//4.3.3 余角与补角12OBAM∠1+∠2=90°∠1+∠2=90°∠AOB=90° 一般地,如果两个角的和等于90°(直角),就说这两个角互为余角.即其中每一个角都是另一个角的余角。两个角互为请你判断:
(1)∠1+∠2=90°则∠1是余角.( ) (2) ∠1 +∠2+ ∠3=90°,则∠1 、∠2、 ∠3、互为余角.( )××互为余角∠1、∠2互为余角∠1是∠2的余角, 或∠2是∠1的余角 一般地,如果两个角的和等于900,就说这两个角互为余角.互为余角几何语言表示为:
若∠1+∠2=90°,那么∠1与∠2互为余角∠1 = 90°—∠2 或:若∠1与∠2互为余角,那么∠1+∠2=90°找朋友图中给出的各角,那些互为余角?10o30o60o80o50o40o43OCDN∠3+∠4=180°∠3+∠4=180°∠DOC=180O 一般地,如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个是另一个角的补角。两个角互为互为补角若∠1+∠2=180°,则∠1与∠2互为补角∠1 = 180°—∠2 反过来说也成立:若∠1与∠2互为补角,那么∠1+∠2=180°几何语言表示为:找朋友图中给出的各角,那些互为补角?10o30o60o80o100o120o150o170o练一练判断题:2、互补的两个角不可能相等。 ( )3、钝角没有余角,但一定有补角( )×1、如果一个角有补角,那么这个角一定是钝角 ( )▲锐角既有余角又有补角; ▲相等的两个角互补, 这两个角是直角;××5、已知∠A=50°,则∠A的余角是____ 补角是____ ,补角与余角的差是_____.40 °130°90°6、一个锐角为X度 ,它的余角为 ______ 度 ,它的补角为 _______ 度,则它的补角比余角大___度.(90- X)(180- X)904、 ∠A=25°37 ,则它的余角 为_______,它的补角为________.判断题: 如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?答:∠2与∠4相等。∠4=90°-∠3∴ ∠2 =∠4∵ ∠1 与∠2互余,∵ ∠3与∠4互余 ,∴∵ ∠1 =∠3,理由如下:等角的余角相等余角的性质这里用到了: 等量减等量,差相等∴ ∠2=90°-∠1 , 如图∠1 与∠C互余,∠2 与∠C互余 ,那么∠1与∠2相等吗?为什么?答:∠1与∠2相等。∠2=90°-∠C∴ ∠1 =∠2∵ ∠1 与∠C互余,∵ ∠2与∠C互余 ,∴理由如下:等角的余角相等余角的性质这里用到了: 等量代换∴ ∠1=90°-∠C ,如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?132143等角的补角相等补角性质活学活用 加深理解1、已知 的补角是105°,则 的余角是多少度?它的余角是1502、如图两堵墙围一个角?AOB,但人不能进入围墙,我们如何去测量这个角的大小呢? 21C?AOB=∠2=1800-∠14、若一个角的补角比它的3倍少20°,求这个角的度数?3、若一个角的补角等于它的余角的4 倍,求这个角的度数。解: 设这个角是x度,则它的补角是 ( 180-x)度,余角是(90-x) 度。根据题意,得:180-x= 4 (90-x)
解得: x =60
答:这个角的度数是60 。这个角的度数是50活学活用 加深理解 5、如图,OD平分∠COA ,OE平分∠COB, 则①∠ EOD=__ °
②图中互余角有 对, 互补角有 对。4590余角、补角的概念:余角、补角的性质:(1) 和为90°的两个角称互为余角;(2) 和为180°的两个角称互为补角;(1) 等角的余角相等; (2) 等角的补角相等;今天我们学了什么?Good Bye请认真观察下图,回答下列问题:挑战一下吧!(2)图中哪几对角是相等的角(直角除外)?为什么?(1)图中有哪几对互余的角?∠A+∠B=90° ∠A+∠2=90°∠1+∠B=90° ∠1+∠2=90°∠B=∠2∠A=∠1B(同角的余角相等)(同角的余角相等)请认真观察下图,回答下列问题:挑战一下吧!(2)图中哪几对角是相等的角(直角除外)?为什么?(1)图中有哪几对互余的角?(∠A+∠B=90°, ∠A+∠C=90°)(∠BOE+∠B=90°, ∠COD+∠C=90°)(∠B=∠C)(∠A=∠BOE)(∠A=∠COD)(∠BOE=∠COD)(同角的余角相等)
学海无涯苦作舟学习目标1.通过丰富的实例,理解角的形成,建立几何中角的概念。
2.掌握角的两种定义形式和四种表示方法。
3.结合实际例子,理解平角、周角的概念。 角是由两条具有公共端点的射线
组成的图形。公共端点顶点射线射线边边判断下列哪些图形是角 (√)(√)(√)(×)角的表示方法O1记作:∠AOB 或∠BOA
或∠O记作∠α记作∠1问题1.如图,能把∠α记作∠O吗?
∠α还可以怎么表示?AOCBα))β2.在上图中共有几个角?分别把他们读出来。牛刀小试把图中的角表示成下列形式:
①∠APO ②∠AOP ③∠OPC,
④∠O ⑤∠COP ⑥∠P。
其中正确的有 (把你认为正确的序号都填上。)① ③ ⑥将图中的角用不同的方法表示出来,并填写下表练习2∠BCE∠2
∠BAC∠DAB∠5
Try a try!
你会表示角吗BCAO已知∠AOB为小于平角的角,以O为顶点的角有几个?3个如果在其内部以O点引一条射线,那么以O为顶点的角有几个?D6个Try a try!
你会数角吗3.如图,以O为顶点的角有几个,请分别把他们
读出来。OABCDE解:共有10个角,
分别是:
∠AOB,∠AOC,
∠AOD,∠AOE,
∠BOC,∠BOD,
∠BOE,∠COD,
∠COE,∠DOE。角也可以看做一条射线绕端点旋转所组成的图形。OBAC 射线OA绕点O旋转,当终点位置OC和起始位置OA
成一直线时,所成的角叫做平角;继续旋转,回到起始
位置OA时,所成的角叫做周角。
平角和周角·始边终边···OAB··OA(B)·顶点说明: 在不做特别说明的情况下,我们说的角都指不大于平角的角如图,棱锥表面上有几个角,请把它们表示出来?练一练 ∠ BAC ∠CAD ∠BAD
∠ABC ∠ABD ∠CBD
∠ACB ∠ACD ∠BCD
∠ ADB ∠ADC ∠BDC考考你选择题:
1.下列语句正确的是( )
A.两条直线相交,组成的图形叫做角
B.两条有公共端点的线段组成的图形叫角
C.两条有公共点的射线组成的图形叫角
D.从同一点引出的两条射线组成的图形叫角
2.下列说法正确的是( )
A.平角是一条直线
B.一条射线是一个周角
C.两条射线组成的图形叫做角
D.两边成一直线的角是平角DD3.判断题
(1)直线是一个平角 ( )
(2)如图(1),点P不在∠AOB的内部 ( )AOB·PABC··DE(3)如图(2), ∠ABC与∠DBE是同一个角( )×× √小结1.角的定义一:
有公共端点的两条射线组成的图形
叫做角,这个公共端点叫做角的顶点,这
两条射线叫做角的边。2.角的定义二:
角可以看成是一条射线绕着它的
端点从一个位置旋转到另一个位置所形成
的图形。射线旋转时经过的平面部分叫角
的内部。3.角的四种表示方法表示方法注意事项1、用三个大写的字母表示表示顶点的字母要写在中间2、用一个顶点的字母来表示一个字母只表示一个角3、用一个数字在靠近顶点的处画上弧线,
并写上数字4、希腊字母表示在靠近顶点的处画上弧线,
并写上希腊字母4.平角、周角的概念创新与应用1.一天24小时中,时钟的时针与分针共组成
多少次平角?多少次周角?
2.某火车站的钟楼上装有一电子报时钟,在
钟面的边界上,每分钟的刻度处都装有一只
小彩灯。晚上九时三十五分二十秒时,时针与分针所夹的角α内装有多少只小彩灯。3.画直线AB,在AB上任取一点O,画射线OC、OD, 这时图中共有几个小于平角的角?分别用三个大写字母表示出来。4.3.2 角的比较与运算记得怎么样比较两条线段的长短方法?即用刻度尺测量线段的
即将其中一条线段移到
3、重叠比较法2、度量法1、观察法 长度的方法。
另一条上作比较。思 考如何比较下列两个角的大小?锐角:00<∠β<900钝角:900< ∠α<1800 1周角>1平角>钝角>1直角>锐角1平角=18001直角=9001周角=3600一:观察法1.将两个角的顶点及一边重合
2. 两个角的另一边落在重合一边的同侧3.由两个角的另一边的位置确定两个角的大小二. 叠合法∠DCE>∠AOB∠DCE<∠AOB∠ DCE =∠AOB三. 度量法1、对“中”—角的顶点对量角器的中心3、读数—读出角的另一边所对的度数2、重合—角的一边与量角器的00刻度
线重合BCA700∠ABC > ∠DEF300比较两个角的大小的方法有三种:观察法
叠合法
度量法小结:两个角的大小关系有三种,记作:
(1) ∠ABC > ∠DEF(2)∠ABC< ∠DEF (3)∠ABC = ∠DEF(E)(F)(E)(F)
A(E)(D)(F)BC 估计图中∠1与∠2的大小关系,
(1)(2)
练习:
并用适当的方法检验.返回下一张上一张退出观察与思考角的大小与角的两边画出的长短有关吗?(1)角的大小与角的两边画出的长短没有关系。
(2)角张开的程度越小,角度就越小结论:迷人数学世界 用放大镜看蚂蚁,用放大镜看自己的手,用放大镜看精致的邮票,用放大镜从太阳光里取火等 等,都会得到令人开心的结果。那么,有没有放大镜放不大的事物呢?你知道放大镜不能“放大”角
的度数的原因吗?
用放大镜来看角因为∠ABC = 700 ,∠DEF=300,
所以∠ABC —∠DEF
=700—300
=400
所以∠ABC — ∠DEF
=∠ABD
三. 角的和与差
700300∠2= ∠1+∠3∠3= ∠2- ∠1∠1= ∠2-∠3三. 角的和差3⌒观 察如图,∠AOC是 ∠AOB与 ∠BOC的和∠AOB是∠AOC与∠BOC的差记作:∠AOC= ∠AOB+ ∠BOC记作:∠AOB=∠AOC—∠BOC类似有∠BOC= ∠AOC—∠AOB图中共有几个角?它们之间有什么关系?
练习2, 如图:∠ AOC = ( ) + ( )
= ( ) - ( ) ∠ BOC=( ) - ( )
= ( ) - ( )∠ AOB∠ BOC∠ AOD∠ COD∠ COD∠ BOD∠ AOC∠ AOB 如图∠ AOB= ∠ COD=900,
∠ AOD=1460, ∠ BOC= ;340D练习3 图中∠1= ∠2, 试判断∠BAD和∠EAC的大小, 并说明理由.冲击解: ∠BAD= ∠2+ ∠DCA
∠EAC= ∠1+∠DCA
探究: 借助一个三角尺可以画出哪些度数的角,用一副三角尺你还能画出哪些度数的角?上台来展示你的结果。75°15°105 °15°120°小结:1、角的大小比较方法:4、三角板可拼出哪些角? 3、角的和差计算 2、角的大小关系有哪些?
动手动脑数一数:图中共有几个小于平角的角,找出规律。(1)(2)123OABCDEFOABCDE(3)(4)……
如果以o为端点,有n条射线,那么组
成的角有多少个?共有(n-1)+(n-2)+(n-3)+…+3+2+1=n(n-1)/2
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线。∵OB平分∠AOC
∴ ∠AOB= ∠BOC= ∠AOC
∠AOC=2 ∠AOB=2 ∠BOC角的三等分线探究1:利用折纸作角平线探究2:利用量角器作角平分线∠AOB=70o70o÷2=35o例题1:已知∠AOB=90o, ∠BOC=30o,OE平分∠AOB,OF平分∠BOC,求∠EOF的度数。解:∵OE平分∠ AOB
∴ ∠EOB= ∠AOB=45o∵OF平分∠ BOC
∴ ∠BOF= ∠BOC=15o∠EOF= ∠EOB+ ∠BOF=45o+15o=60o例题2:如图, ∠AOC=62o, ∠BOD=100o,OE平分∠BOD,OB平分∠AOC,求∠BOE、 ∠COE、 ∠AOE的度数。1.如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55o,则∠BOD的度数是( )
A.35o B.55o
C.70o D.110o2.若将一个平角三等分,则两旁两个角的平分线组成的角是( )
A.90o B.120o C.100o D.105o
3.如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=25o,则∠AOB等于( )
A.50oB.70oC.20oD.100o4.如图1, ∠COD=116o, ∠BOD=90o,OA平分∠BOC,求∠AOB的度数.
5.如图2,已知直线AB,CD相交于点O,OA平分∠EOC, ∠EOC=70o,求∠BOD的度数.角度的换算一周角=2平角=4直角=3600
一平角=1800
一直角=900
10=60/ 1/=60//
(读成1度等于60分,1分等于60秒 )
请你要牢记哟!例题 1 填空
(1)34.50= 0 /
(2)112.270= 0 / //
解:(1)34.50=340+0.50
=340+0.5×60/
=340+3 0/=34030/
(2)112.270=1120+0.27×60/
=1120+16.2/
=1120+16/+0.2×60//
=112016/12//3430112161210=60/
1/=60//例题2 把下列各题结果化成度
72036/ (2)37014/24//
解:(1)72036/=720+36/
=720+(36÷60)0
=720+0.60
=72.60
(2)37014/24//=370+14/+24//
=370+14/+(24÷60)/
=370+14/+0.4/
=370+14.4/
=370+(14.4÷60)0
=370+0.240=37.240例题3 计算(1) 12036/56// + 45024/35//
解:(1)原式=(12+45)0+(36+24)/+(56+35)//
=570+60/+91//
=570+61/+31//
=580+1/+31//
=5801/31//这里的加与减,要将度与度、分与分、秒与秒分别相加时逢60进位,相减时要借1作60.(2) 79045/ - 61048/49//
解:原式=79044/60//- 61048/49//
=780104/60// - 61048/49//
=(78 -61)0 + (104 -48)/ + (60-49)//
=17056/11//
(3)21031/27//×3
解:原式=(21×3)0+ (31×3)/+ (27×3)//
=63093/81//
=63094/21//
=64034/21//(4) 63021/39//÷3
解:原式=(63÷3)0+ (21÷3)/+ (39÷3)//
=2107/13//
(5)10606/25//÷5
解:原式=(106÷5)0+ (6÷5)/+ (25÷5)//
=210+ (66÷5)/ + (25÷5)//
=210+13/+ (85÷5)//
=21013/17//4.3.3 余角与补角12OBAM∠1+∠2=90°∠1+∠2=90°∠AOB=90° 一般地,如果两个角的和等于90°(直角),就说这两个角互为余角.即其中每一个角都是另一个角的余角。两个角互为请你判断:
(1)∠1+∠2=90°则∠1是余角.( ) (2) ∠1 +∠2+ ∠3=90°,则∠1 、∠2、 ∠3、互为余角.( )××互为余角∠1、∠2互为余角∠1是∠2的余角, 或∠2是∠1的余角 一般地,如果两个角的和等于900,就说这两个角互为余角.互为余角几何语言表示为:
若∠1+∠2=90°,那么∠1与∠2互为余角∠1 = 90°—∠2 或:若∠1与∠2互为余角,那么∠1+∠2=90°找朋友图中给出的各角,那些互为余角?10o30o60o80o50o40o43OCDN∠3+∠4=180°∠3+∠4=180°∠DOC=180O 一般地,如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个是另一个角的补角。两个角互为互为补角若∠1+∠2=180°,则∠1与∠2互为补角∠1 = 180°—∠2 反过来说也成立:若∠1与∠2互为补角,那么∠1+∠2=180°几何语言表示为:找朋友图中给出的各角,那些互为补角?10o30o60o80o100o120o150o170o练一练判断题:2、互补的两个角不可能相等。 ( )3、钝角没有余角,但一定有补角( )×1、如果一个角有补角,那么这个角一定是钝角 ( )▲锐角既有余角又有补角; ▲相等的两个角互补, 这两个角是直角;××5、已知∠A=50°,则∠A的余角是____ 补角是____ ,补角与余角的差是_____.40 °130°90°6、一个锐角为X度 ,它的余角为 ______ 度 ,它的补角为 _______ 度,则它的补角比余角大___度.(90- X)(180- X)904、 ∠A=25°37 ,则它的余角 为_______,它的补角为________.判断题: 如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?答:∠2与∠4相等。∠4=90°-∠3∴ ∠2 =∠4∵ ∠1 与∠2互余,∵ ∠3与∠4互余 ,∴∵ ∠1 =∠3,理由如下:等角的余角相等余角的性质这里用到了: 等量减等量,差相等∴ ∠2=90°-∠1 , 如图∠1 与∠C互余,∠2 与∠C互余 ,那么∠1与∠2相等吗?为什么?答:∠1与∠2相等。∠2=90°-∠C∴ ∠1 =∠2∵ ∠1 与∠C互余,∵ ∠2与∠C互余 ,∴理由如下:等角的余角相等余角的性质这里用到了: 等量代换∴ ∠1=90°-∠C ,如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?132143等角的补角相等补角性质活学活用 加深理解1、已知 的补角是105°,则 的余角是多少度?它的余角是1502、如图两堵墙围一个角?AOB,但人不能进入围墙,我们如何去测量这个角的大小呢? 21C?AOB=∠2=1800-∠14、若一个角的补角比它的3倍少20°,求这个角的度数?3、若一个角的补角等于它的余角的4 倍,求这个角的度数。解: 设这个角是x度,则它的补角是 ( 180-x)度,余角是(90-x) 度。根据题意,得:180-x= 4 (90-x)
解得: x =60
答:这个角的度数是60 。这个角的度数是50活学活用 加深理解 5、如图,OD平分∠COA ,OE平分∠COB, 则①∠ EOD=__ °
②图中互余角有 对, 互补角有 对。4590余角、补角的概念:余角、补角的性质:(1) 和为90°的两个角称互为余角;(2) 和为180°的两个角称互为补角;(1) 等角的余角相等; (2) 等角的补角相等;今天我们学了什么?Good Bye请认真观察下图,回答下列问题:挑战一下吧!(2)图中哪几对角是相等的角(直角除外)?为什么?(1)图中有哪几对互余的角?∠A+∠B=90° ∠A+∠2=90°∠1+∠B=90° ∠1+∠2=90°∠B=∠2∠A=∠1B(同角的余角相等)(同角的余角相等)请认真观察下图,回答下列问题:挑战一下吧!(2)图中哪几对角是相等的角(直角除外)?为什么?(1)图中有哪几对互余的角?(∠A+∠B=90°, ∠A+∠C=90°)(∠BOE+∠B=90°, ∠COD+∠C=90°)(∠B=∠C)(∠A=∠BOE)(∠A=∠COD)(∠BOE=∠COD)(同角的余角相等)
