2021-2022学年人教版数学八年级下册18.1.1平行四边形的性质课后提升(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册18.1.1平行四边形的性质课后提升(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 560.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 23:40:37 | ||
图片预览



文档简介
平行四边形的性质
一、单选题
1.在平行四边形ABCD中,∠A ∶∠ B ∶∠ C ∶∠ D的值可以是( )
A.1∶2∶3∶4 B.1∶2∶2∶1 C.2∶2∶1∶1 D.1∶2∶1∶2
2.的周长为32cm,AB:BC=3:5,则AB、BC的长分别为( )
A.20cm,12cm B.10cm,6cm C.6cm,10cm D.12cm,20cm
3.如图,在ABCD中,AB=3,AD=5,∠ABC的平分线BE交AD于点E,则DE的长是( ).
A.4 B.3 C.3.5 D.2
4.在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,AE=4,AF=6,平行四边形ABCD的周长为40,则平行四边形ABCD的面积是( )
A.36 B.48 C.40 D.24
5.如图,平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 B.2 C.3 D.4
6.如图,口ABCD的对角线AC,BD相交于点O,且,若△BCO的周长为14,则AD的长为( )
A.12 B.9 C.8 D.6
7.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=128°,则∠A=( )
A.32° B.42° C.52° D.62°
8.如图,在 ABCD中,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,若△CDE的周长为8,则 ABCD的周长为( )
A.8 B.10 C.16 D.20
9.在平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(7,3) B.(8,2) C.(3,7) D.(5,3)
10.如图所示,在 ABCD中,对角线AC,BD相交于点O,过点O的直线EF分别交AD于点E,BC于点F, ,则 ABCD的面积为( )
A.24 B.32 C.40 D.48
11.如图,在 ABCD中,AB=2,BC=4,∠D=60°,点P、Q分别是AC和BC上的动点,在点P和点Q运动的过程中,PB+PQ的最小值为( )
A.4 B.3 C.2 D.4
12.如图,已知,∠ABC=60°,BC=2AB=8,点C关于AD的对称点为E,连接BE交AD于点F,点G为CD的中点,连接EG、BG,则=( )
A. B. C. D.
二、填空题
13.如图,已知平行四边形ABCD的周长为80,两边上的高,,则平行四边形ABCD的面积是______.
14.如图,P是平行四边形ABCD对角线AC上的点,且满足PB=PC=CD,若∠PCB=20°,则∠D的度数是______.
15.如图,在平行四边形中,对角线的垂直平分线交于点,连接.若平行四边形的周长为20cm,则的周长为______cm.
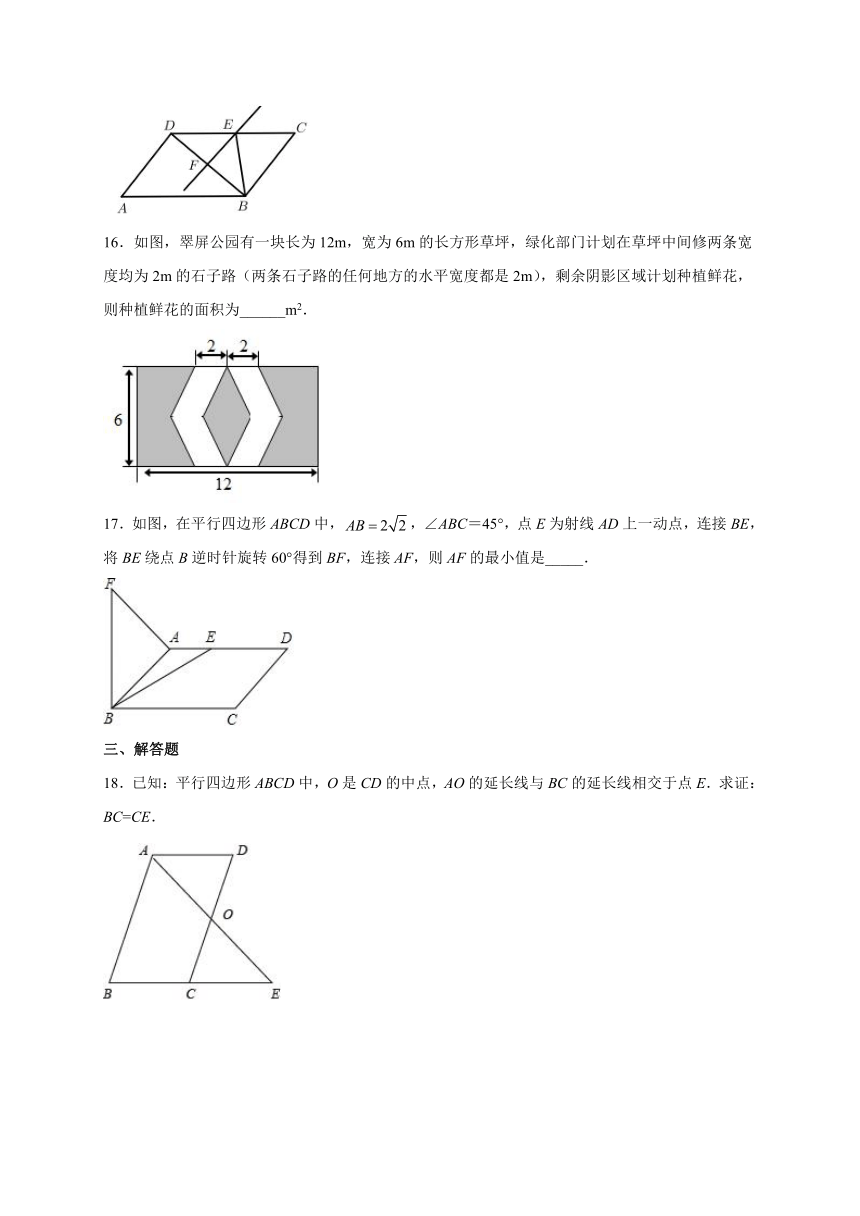
16.如图,翠屏公园有一块长为12m,宽为6m的长方形草坪,绿化部门计划在草坪中间修两条宽度均为2m的石子路(两条石子路的任何地方的水平宽度都是2m),剩余阴影区域计划种植鲜花,则种植鲜花的面积为______m2.
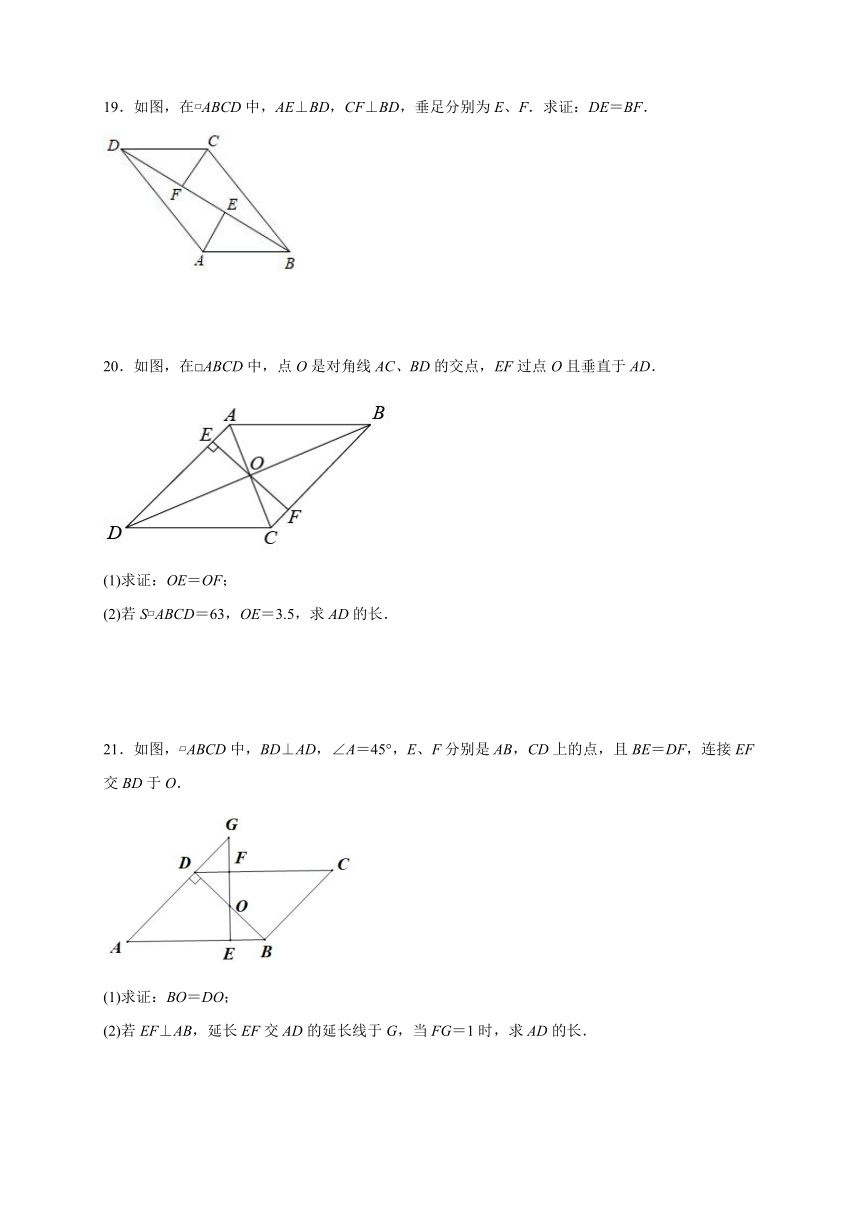
17.如图,在平行四边形ABCD中,,∠ABC=45°,点E为射线AD上一动点,连接BE,将BE绕点B逆时针旋转60°得到BF,连接AF,则AF的最小值是_____.
三、解答题
18.已知:平行四边形ABCD中,O是CD的中点,AO的延长线与BC的延长线相交于点E.求证:BC=CE.
19.如图,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:DE=BF.
20.如图,在□ABCD中,点O是对角线AC、BD的交点,EF过点O且垂直于AD.
(1)求证:OE=OF;
(2)若S ABCD=63,OE=3.5,求AD的长.
21.如图, ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
22.如(图1),点为对角线上一点,连接,.
(1)求证:;
(2)如(图2),若,为线段上一点,且,连接,设,,求与的函数表达式;
(3)在(2)的条件下,如(图3),点为线段上(不与点、点重合)任意一点,试判断以、、为边的三角形的形状,并说明理由.
试卷第1页,共3页
参考答案:
1.D
解:略
2.C
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,
∵AB:BC=3:5,
∴可设 ,
∵的周长为32cm,
∴ ,即 ,
解得: ,
∴ .
故选:C
3.D
解:∵ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠CBE,
BE是∠ABC的角平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴三角形ABE是等腰三角形,
∴AE=AB=3,
∴DE=AD-AE=5-3=2,
故选:D.
4.B
解:设BC=x,
∵ ABCD的周长为40,
∴CD=20-x,
∵ ABCD的面积=BC AE=CD AF,
∴4x=6(20-x),
解得x=12,
∴ ABCD的面积=BC AE=12×4=48.
故选:B.
5.B
解:∵四边形ABCD为平行四边形,
∴,
∴,
∵AE平分,
∴,
∴,
∴,
∵,
∴,
故选:B.
6.D
解:四边形是平行四边形,
,,
,
,
的周长为14,
,
故选:D.
7.C
解:∵∠DCE=128°,
∴∠DCB=180°-∠DCE=180°-128°=52°,
∵四边形ABCD是平行四边形,
∴∠A=∠DCB=52°,
故选:C.
8.C
解:∵四边形ABCD是平行四边形,
∴OA=OC,AB=CD,AD=BC,
∵OE⊥AC,
∴OE是线段AC的垂直平分线,
∴AE=CE,
∵△CDE的周长为8,
∴CE+DE+CD=8,即AD+CD =8,
∴平行四边形ABCD的周长为2(AD+CD)=16.
故选:C.
9.A
解: 四边形ABCD为平行四边形。
且。
C点和D的纵坐标相等,都为3.
A点坐标为(0,0),B点坐标为(5,0),
.
D点坐标为(2,3),
C点横坐标为,
点坐标为(7,3).
故选:A.
10.B
解:∵四边形是平行四边形,
,
,
在和中,
∵,
,
,
,
则的面积为,
故选:B.
11.C
解:取BC的中点G,连接AG.在 ABCD中,AB=2,BC=4,∠D=60°,
∴AB=BG=2,∠ABG=∠D=60°,
∴△ABG是等边三角形,
∴AG=GC=2,∠AGB=∠BAG=60°,
∴∠GAC=∠GCA=30°,
∴∠BAC=90°,
作点B关于AC的对称点F,连接GF, 交AC于点P,由对称可知,B、A、F在一条直线上,AG=AF,
∵∠BAG=∠F+∠AGF=60°,
∴∠F=∠AGF=30°,
∴∠FGB=90°,
当点Q与点G重合时,PB+PQ=PF+PG=FG,FG的长即为PB+PQ的最小值,
∵∠F=∠AGF=30°,AG=GC=2,
∴BF=4,
,
∴BP+PQ的最小值为2.
故选:C.
12.B
解:如图,取BC中点H,连接AH,连接CE交AD于N,作交CD的延长线于M,
∵,,,
∴,
∴是等边三角形,
∴,
∴,,
∵, ,
∴ , ,
∵,
∴,,
∴ ,,
∴
故选:B
13.75
解:如图,连接,
∵,∴,
∵,
∴,
,
∴,
∴,,
∴.
故答案为:
14.
解:,
,
,
四边形是平行四边形,
,
,
,
,
,
,
故答案为:.
15.10
解:∵的垂直平分线交于点,交于点,
∴,
∵平行四边形的周长为20cm,
∴,
∴,
∴的周长
.
故答案为:10.
16.48
解:根据题意得:种植鲜花的面积为 .
故答案为:48
17.
解:如图,以AB为边向下作等边△ABK,连接EK,在EK上取一点T,使得AT=TK.
∵BE=BF,BK=BA,∠EBF=∠ABK=60°,
∴∠ABF=∠KBE,
∴△ABF≌△KBE(SAS),
∴AF=EK,
根据垂线段最短可知,当KE⊥AD时,KE的值最小,
∵四边形ABCD是平行四边形,
∴ADBC,
∵∠ABC=45°,
∴∠BAD=180°﹣∠ABC=135°,
∵∠BAK=60°,
∴∠EAK=75°,
∵∠AEK=90°,
∴∠AKE=15°,
∵TA=TK,
∴∠TAK=∠AKT=15°,
∴∠ATE=∠TAK+∠AKT=30°,
设AE=a,则AT=TK=2a,ET=a,
在Rt△AEK中,∵AK2=AE2+EK2,
∴a2+(2a+a)2=4,
∴a=,
∴EK=2a+a=,
∴AF的最小值为:.
故答案为:.
18.证明见详解
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADO=∠OCE,
∵点O是CD的中点,
∴DO=CO,
在△AOD和△EOC中
,
∴△AOD≌△EOC(ASA),
∴AD=EC,
∴BC=CE.
19.见解析
解:∵四边形ABCD是平行四边形,
∴AD=CB,,
∴∠ADE=∠CBF,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(AAS),
∴DE=BF.
20.(1)证明见解析
(2)9
(1)
解:∵四边形ABCD是平行四边形,O是AC与BD的交点,
∴AO=CO,AD∥BC,
∴∠OAE=∠OCF,∠OEA=∠OFC,
∴△AOE≌△COF(AAS),
∴OE=OF;
(2)
解:由(1)得OE=OF=3.5,
∴EF=7,
∵AD∥BC,EF⊥AD,
∴EF的长即为平行四边形ABCD中AD边上的高,
∵四边形ABCD的面积为63,
∴,
∴AD=9.
21.(1)详见解析
(2)详见解析
(1)
证明:∵四边形ABCD是平行四边形,
∴,
∴,
在与中
∴,
∴.
(2)
解:∵,
∴,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,
∴为等腰直角三角形,
∴,
∴,
∵,
∴,
∴,
∴,
由(1),
∴,
∴,
∴,
故答案为:.
22.(1)证明见解析过程;(2);(3)以、、为边的三角形是直角三角形
解:(1)四边形是平行四边形,
,,
,,
,
,,
,
;
(2),
,
,
,,
,
,
,
,
;
(3)设,
当时,如图3,
,,
,
,,
,
以、、为边的三角形是直角三角形;
当时,过点作于,
,
,
,
,,
,
以、、为边的三角形是直角三角形;
综上所述:以、、为边的三角形是直角三角形;
答案第1页,共2页
一、单选题
1.在平行四边形ABCD中,∠A ∶∠ B ∶∠ C ∶∠ D的值可以是( )
A.1∶2∶3∶4 B.1∶2∶2∶1 C.2∶2∶1∶1 D.1∶2∶1∶2
2.的周长为32cm,AB:BC=3:5,则AB、BC的长分别为( )
A.20cm,12cm B.10cm,6cm C.6cm,10cm D.12cm,20cm
3.如图,在ABCD中,AB=3,AD=5,∠ABC的平分线BE交AD于点E,则DE的长是( ).
A.4 B.3 C.3.5 D.2
4.在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,AE=4,AF=6,平行四边形ABCD的周长为40,则平行四边形ABCD的面积是( )
A.36 B.48 C.40 D.24
5.如图,平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 B.2 C.3 D.4
6.如图,口ABCD的对角线AC,BD相交于点O,且,若△BCO的周长为14,则AD的长为( )
A.12 B.9 C.8 D.6
7.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=128°,则∠A=( )
A.32° B.42° C.52° D.62°
8.如图,在 ABCD中,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,若△CDE的周长为8,则 ABCD的周长为( )
A.8 B.10 C.16 D.20
9.在平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(7,3) B.(8,2) C.(3,7) D.(5,3)
10.如图所示,在 ABCD中,对角线AC,BD相交于点O,过点O的直线EF分别交AD于点E,BC于点F, ,则 ABCD的面积为( )
A.24 B.32 C.40 D.48
11.如图,在 ABCD中,AB=2,BC=4,∠D=60°,点P、Q分别是AC和BC上的动点,在点P和点Q运动的过程中,PB+PQ的最小值为( )
A.4 B.3 C.2 D.4
12.如图,已知,∠ABC=60°,BC=2AB=8,点C关于AD的对称点为E,连接BE交AD于点F,点G为CD的中点,连接EG、BG,则=( )
A. B. C. D.
二、填空题
13.如图,已知平行四边形ABCD的周长为80,两边上的高,,则平行四边形ABCD的面积是______.
14.如图,P是平行四边形ABCD对角线AC上的点,且满足PB=PC=CD,若∠PCB=20°,则∠D的度数是______.
15.如图,在平行四边形中,对角线的垂直平分线交于点,连接.若平行四边形的周长为20cm,则的周长为______cm.
16.如图,翠屏公园有一块长为12m,宽为6m的长方形草坪,绿化部门计划在草坪中间修两条宽度均为2m的石子路(两条石子路的任何地方的水平宽度都是2m),剩余阴影区域计划种植鲜花,则种植鲜花的面积为______m2.
17.如图,在平行四边形ABCD中,,∠ABC=45°,点E为射线AD上一动点,连接BE,将BE绕点B逆时针旋转60°得到BF,连接AF,则AF的最小值是_____.
三、解答题
18.已知:平行四边形ABCD中,O是CD的中点,AO的延长线与BC的延长线相交于点E.求证:BC=CE.
19.如图,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:DE=BF.
20.如图,在□ABCD中,点O是对角线AC、BD的交点,EF过点O且垂直于AD.
(1)求证:OE=OF;
(2)若S ABCD=63,OE=3.5,求AD的长.
21.如图, ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
22.如(图1),点为对角线上一点,连接,.
(1)求证:;
(2)如(图2),若,为线段上一点,且,连接,设,,求与的函数表达式;
(3)在(2)的条件下,如(图3),点为线段上(不与点、点重合)任意一点,试判断以、、为边的三角形的形状,并说明理由.
试卷第1页,共3页
参考答案:
1.D
解:略
2.C
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,
∵AB:BC=3:5,
∴可设 ,
∵的周长为32cm,
∴ ,即 ,
解得: ,
∴ .
故选:C
3.D
解:∵ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠CBE,
BE是∠ABC的角平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴三角形ABE是等腰三角形,
∴AE=AB=3,
∴DE=AD-AE=5-3=2,
故选:D.
4.B
解:设BC=x,
∵ ABCD的周长为40,
∴CD=20-x,
∵ ABCD的面积=BC AE=CD AF,
∴4x=6(20-x),
解得x=12,
∴ ABCD的面积=BC AE=12×4=48.
故选:B.
5.B
解:∵四边形ABCD为平行四边形,
∴,
∴,
∵AE平分,
∴,
∴,
∴,
∵,
∴,
故选:B.
6.D
解:四边形是平行四边形,
,,
,
,
的周长为14,
,
故选:D.
7.C
解:∵∠DCE=128°,
∴∠DCB=180°-∠DCE=180°-128°=52°,
∵四边形ABCD是平行四边形,
∴∠A=∠DCB=52°,
故选:C.
8.C
解:∵四边形ABCD是平行四边形,
∴OA=OC,AB=CD,AD=BC,
∵OE⊥AC,
∴OE是线段AC的垂直平分线,
∴AE=CE,
∵△CDE的周长为8,
∴CE+DE+CD=8,即AD+CD =8,
∴平行四边形ABCD的周长为2(AD+CD)=16.
故选:C.
9.A
解: 四边形ABCD为平行四边形。
且。
C点和D的纵坐标相等,都为3.
A点坐标为(0,0),B点坐标为(5,0),
.
D点坐标为(2,3),
C点横坐标为,
点坐标为(7,3).
故选:A.
10.B
解:∵四边形是平行四边形,
,
,
在和中,
∵,
,
,
,
则的面积为,
故选:B.
11.C
解:取BC的中点G,连接AG.在 ABCD中,AB=2,BC=4,∠D=60°,
∴AB=BG=2,∠ABG=∠D=60°,
∴△ABG是等边三角形,
∴AG=GC=2,∠AGB=∠BAG=60°,
∴∠GAC=∠GCA=30°,
∴∠BAC=90°,
作点B关于AC的对称点F,连接GF, 交AC于点P,由对称可知,B、A、F在一条直线上,AG=AF,
∵∠BAG=∠F+∠AGF=60°,
∴∠F=∠AGF=30°,
∴∠FGB=90°,
当点Q与点G重合时,PB+PQ=PF+PG=FG,FG的长即为PB+PQ的最小值,
∵∠F=∠AGF=30°,AG=GC=2,
∴BF=4,
,
∴BP+PQ的最小值为2.
故选:C.
12.B
解:如图,取BC中点H,连接AH,连接CE交AD于N,作交CD的延长线于M,
∵,,,
∴,
∴是等边三角形,
∴,
∴,,
∵, ,
∴ , ,
∵,
∴,,
∴ ,,
∴
故选:B
13.75
解:如图,连接,
∵,∴,
∵,
∴,
,
∴,
∴,,
∴.
故答案为:
14.
解:,
,
,
四边形是平行四边形,
,
,
,
,
,
,
故答案为:.
15.10
解:∵的垂直平分线交于点,交于点,
∴,
∵平行四边形的周长为20cm,
∴,
∴,
∴的周长
.
故答案为:10.
16.48
解:根据题意得:种植鲜花的面积为 .
故答案为:48
17.
解:如图,以AB为边向下作等边△ABK,连接EK,在EK上取一点T,使得AT=TK.
∵BE=BF,BK=BA,∠EBF=∠ABK=60°,
∴∠ABF=∠KBE,
∴△ABF≌△KBE(SAS),
∴AF=EK,
根据垂线段最短可知,当KE⊥AD时,KE的值最小,
∵四边形ABCD是平行四边形,
∴ADBC,
∵∠ABC=45°,
∴∠BAD=180°﹣∠ABC=135°,
∵∠BAK=60°,
∴∠EAK=75°,
∵∠AEK=90°,
∴∠AKE=15°,
∵TA=TK,
∴∠TAK=∠AKT=15°,
∴∠ATE=∠TAK+∠AKT=30°,
设AE=a,则AT=TK=2a,ET=a,
在Rt△AEK中,∵AK2=AE2+EK2,
∴a2+(2a+a)2=4,
∴a=,
∴EK=2a+a=,
∴AF的最小值为:.
故答案为:.
18.证明见详解
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADO=∠OCE,
∵点O是CD的中点,
∴DO=CO,
在△AOD和△EOC中
,
∴△AOD≌△EOC(ASA),
∴AD=EC,
∴BC=CE.
19.见解析
解:∵四边形ABCD是平行四边形,
∴AD=CB,,
∴∠ADE=∠CBF,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(AAS),
∴DE=BF.
20.(1)证明见解析
(2)9
(1)
解:∵四边形ABCD是平行四边形,O是AC与BD的交点,
∴AO=CO,AD∥BC,
∴∠OAE=∠OCF,∠OEA=∠OFC,
∴△AOE≌△COF(AAS),
∴OE=OF;
(2)
解:由(1)得OE=OF=3.5,
∴EF=7,
∵AD∥BC,EF⊥AD,
∴EF的长即为平行四边形ABCD中AD边上的高,
∵四边形ABCD的面积为63,
∴,
∴AD=9.
21.(1)详见解析
(2)详见解析
(1)
证明:∵四边形ABCD是平行四边形,
∴,
∴,
在与中
∴,
∴.
(2)
解:∵,
∴,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,
∴为等腰直角三角形,
∴,
∴,
∵,
∴,
∴,
∴,
由(1),
∴,
∴,
∴,
故答案为:.
22.(1)证明见解析过程;(2);(3)以、、为边的三角形是直角三角形
解:(1)四边形是平行四边形,
,,
,,
,
,,
,
;
(2),
,
,
,,
,
,
,
,
;
(3)设,
当时,如图3,
,,
,
,,
,
以、、为边的三角形是直角三角形;
当时,过点作于,
,
,
,
,,
,
以、、为边的三角形是直角三角形;
综上所述:以、、为边的三角形是直角三角形;
答案第1页,共2页
