2021-2022学年人教版数学八年级下册18.1.2平行四边形的判定课后提升(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册18.1.2平行四边形的判定课后提升(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 574.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 23:43:48 | ||
图片预览




文档简介
平行四边形的判定
一、单选题
1.下面给出的是四边形ABCD中,AB,BC,CD,DA的长度之比,其中能满足四边形ABCD是平行四边形的是( )
A.1:2:3:4 B.2:2:3:3 C.2:3:2:3 D.2:3:3:2
2.下列条件中,能判定四边形是平行四边形的是( )
A.一组对边相等,另一组对边平行 B.对角线互相垂直
C.一组对边相等,一组对角相等 D.一组对边平行,一组对角相等
3. ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AF∥CE C.CE=AF D.∠DAF=∠BCE
4.如图,中,点D、E、F分别为边的中点,则下列关于线段和之间关系的说法中正确的是( )
A. B.
C.和互相平分 D.以上答案都不对
5.如图,已知在中,,,分别是边,,的中点,,,则四边形AFDE的周长等于( )
A.18 B.16 C.14 D.12
6.如图,已知四边形ABCD和四边形BCEF均为平行四边形,∠D=60°,连接AF,并延长交BE于点P,若AP⊥BE,AB=3,BC=2,AF=1,则BE的长为( )
A.5 B.2 C.2 D.3
7.如图,在△ABC中,F为BC的中点,点E是AC边上的一点,且AC=10,当AE的长为( )时,EF∥AB
A.3 B.4 C.5 D.4.5
8.如图,在平行四边形中,为对角线,点是的中点,且,,四边形的周长为10,则平行四边形的周长为( )
A.10 B.12 C.15 D.20
9.如图,某花木场有一块如四边形形状的空地,其中,其各边中点分别是E、F、G、H,测得对角线,现想利用篱笆围成四边形场地,则需篱笆的总长度是( )
A. B. C. D.
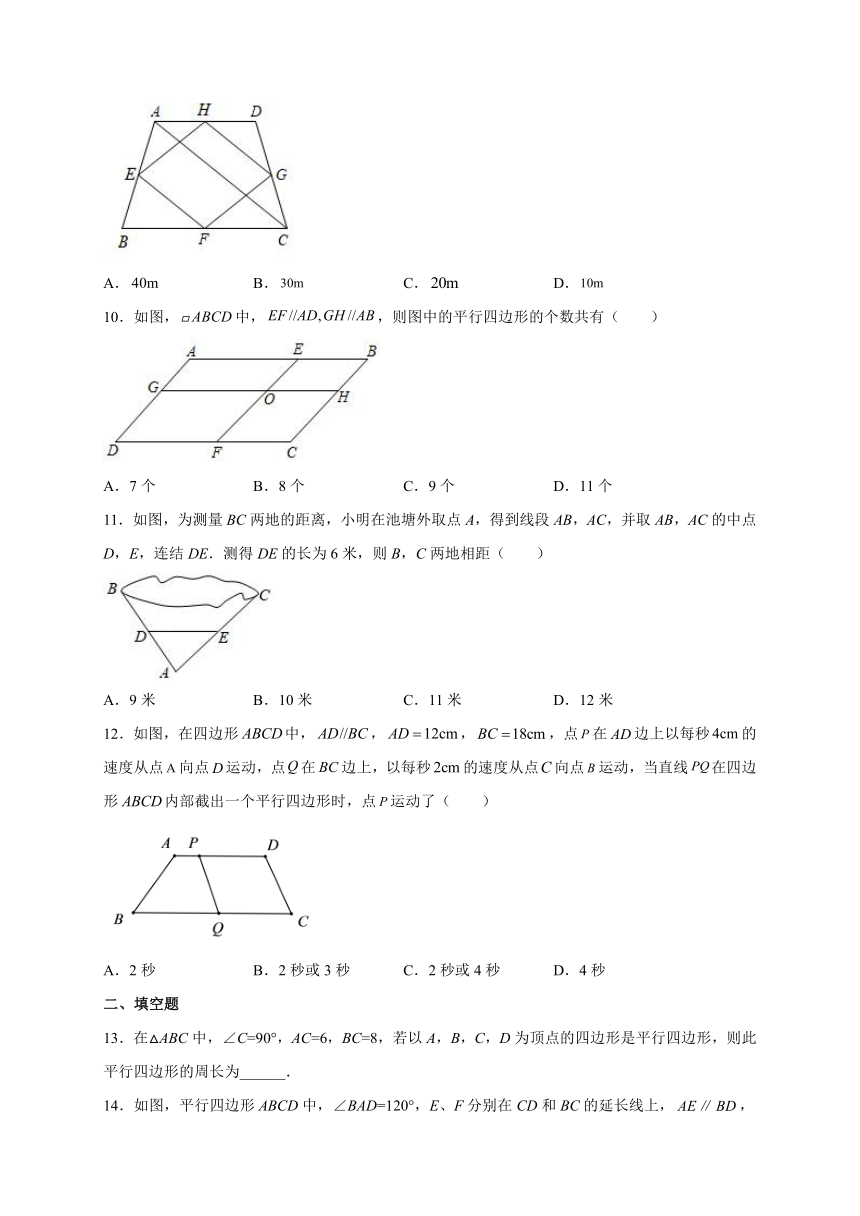
10.如图,中,,则图中的平行四边形的个数共有( )
A.7个 B.8个 C.9个 D.11个
11.如图,为测量BC两地的距离,小明在池塘外取点A,得到线段AB,AC,并取AB,AC的中点D,E,连结DE.测得DE的长为6米,则B,C两地相距( )
A.9米 B.10米 C.11米 D.12米
12.如图,在四边形中,,,,点在边上以每秒的速度从点向点运动,点在边上,以每秒的速度从点向点运动,当直线在四边形内部截出一个平行四边形时,点运动了( )
A.2秒 B.2秒或3秒 C.2秒或4秒 D.4秒
二、填空题
13.在△ABC中,∠C=90°,AC=6,BC=8,若以A,B,C,D为顶点的四边形是平行四边形,则此平行四边形的周长为______.
14.如图,平行四边形ABCD中,∠BAD=120°,E、F分别在CD和BC的延长线上,,EF⊥BC,,则AB的长是______.
15.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E、F分别是线段AO,BO的中点,若AC+BD=12cm,△OAB的周长是10cm,则EF=______cm.
16.如图,四边形ABCD中,∠C=90°,BC=3,CD=3,点P为线段BC上的动点,点E、点F分别为线段AD、AP的中点,则EF长度的最大值为 ___.
17.如图,在 ABCD中,点E是对角线AC上一点,过点E作AC的垂线,交边AD于点P,交边BC于点Q,连接PC、AQ,若AC=6,PQ=4,则PC+AQ的最小值为________________.
三、解答题
18.如图,在中,,点,,分别在边,,上, ,,.求四边形的周长.
19.已知:如图,在 ABCD中,E,F分别为BC和AD上的点,BD和EF相交于点O,且OE=OF.求证:四边形AECF为平行四边形.
20.如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长与AD的延长线交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若BC=BD,求BF的长.
21.如图,AD∥BC,点E是AB的中点,联结DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:AD=BF;
(2)当点G是FC的中点时,判断△FDC的形状.
22.点E是 ABCD的边CD上的一点,连接EA并延长,使EA=AM,连接EB并延长,使EB=BN,连接MN,F为MN的中点,连接CF,DM.
(1)求证:四边形DMFC是平行四边形;
(2)连接EF,交AB于点O,若OF=2,求EF的长.
23.已知,如图在中,对角线和相交于点,点,分别在,上,且,连接,.
(1)如图1,求证:;
(2)如图2,延长交于点,延长交于点.求证:.
试卷第1页,共3页
参考答案:
1.C
解:A、,则不能判定是平行四边形,故本选项不符合题意;
B、,则不能判定是平行四边形,故本选项不符合题意;
C、,根据两组对边分别相等的四边形是平行四边形,则能判定是平行四边形,故本选项符合题意;
D、,则不能判定是平行四边形,故本选项不符合题意;
故选:C
2.D
解:A、一组对边相等,另一组对边平行的四边形是等腰梯形,不一定是平行四边形,故选项不符合题意;
B、对角线互相垂直的四边形不一定是平行四边形,故选项不符合题意;
C、由一组邻边相等,一组对角相等,不能判定一个四边形是平行四边形,故选项不符合题意;
D、一组对角相等,一组对边平行,可得到任意两对邻角互补,那么可得到两组对边分别平行,为平行四边形,故选项符合题意;
故选D.
3.C
解:如图,连接AC与BD相交于O,
在 ABCD中,OA=OC,OB=OD,要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项不符合题意;
B、AF∥CE能够利用“角角边”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意;
C、若CE=AF,则无法判断OE=OE,故本选项符合题意;
D、由∠DAF=∠BCE,从而可得△DAF≌△BCE,然后得出∠DFA=∠BEC,
∴∠AFE=∠CEF,
∴AF∥CE,
结合选项B可证明四边形AECF是平行四边形,故本选项不符合题意;
故选:C.
4.C
解:如图,连接FD,ED,
∵,点D、E、F分别为边BC、CA、AB的中点,
∴DE,DF,EF都是△ABC的中位线,
∴DF∥AC,DE∥AB,
∴四边形AEDF是平行四边形,
∴EF与AD互相平分,故C符合题意,D不符合题意;
根据现有条件,无法推出AD=EF,AD⊥EF,故A、B不符合题意,
故选C.
5.A
解:∵D,E,F分别是边BC,CA,AB的中点.AB=10,AC=8,
∴DE=AB=5,DF=AC=4,AF=AB=5,AE=AC=4,
∴四边形AFDE的周长=AF+DF+DE+AE=5+5+4+4=18,
故选:A.
6.D
解:过点D作DH⊥BC,交BC的延长线于点H,连接BD,DE,
∵四边形ABCD是平行四边形,AB=3,∠ADC=60 ,
∴CD=AB=3,∠DCH=∠ABC=∠ADC=60 ,
∵DH⊥BC,
∴∠DHC=90 ,∴∠ADC+∠CDH=90°,∴∠CDH=30°,
在Rt△DCH中,CH=CD=,DH=,
∴,
∵四边形BCEF是平行四边形,
∴AD=BC=EF,AD∥EF,
∴四边形ADEF是平行四边形,
∴AF∥DE,AF=DE=1,
∵AF⊥BE,
∴DE⊥BE,
∴,
∴,
故选D.
7.C
解:当为的中点时,∵F为BC的中点
∴为的中位线,
∴
此时
故选C
8.D
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵点O是BD的中点,且AD//EO,OF//AB,
∴OE,OF分别是三角形ABD,三角形BCD的中位线,BC//EO,
∴四边形OEBF是平行四边形,AD=2OE,CD=2OF,OE=BF,OF=BE,
∵四边形OEBF的周长为10,
∴OE+BE+BF+OF=10,
∴OE+OF=5,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴四边形ABCD的周长=AB+BC+AD+CD=2(AD+CD)=4(OE+OF)=20,
故选D.
9.C
解:过点A作AM∥DC交BC于点M,连接BD
则∠DCB=∠AMB
∵∠DCB=∠ABC
∴∠AMB=∠ABC
∴AM=AB
∵AD∥BC,AM∥DC
∴四边形AMCD是平行四边形
∴AM=DC
∴AB=DC
在△ABC与△DCB中
∴△ABC≌△DCB(SAS)
∴BD=AC=10m
∵E、F、G、H分别为AB、BC、CD、AD的中点
∴GH=EF=,EH=FG=
∴四边形EFGH是平行四边形
则篱笆的总长度为2(GH+EH)=20(m)
故选:C.
10.C
解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,
则图中的四边形AEOG、ABHG、AEFD、ABCD、
GOFD、GHCD、EBHO、EBCF和OHCF都是平行四边形,
共9个,
故选:C.
11.D
解:∵点D,E分别为AB,AC的中点,
∴DE是△ABC的中位线,
∴DE=BC,
∴BC=2DE=2×6=12(米),
故选:D.
12.B
解:设点、运动的时间为秒,依题意得,
,,,,
①当时,四边形是平行四边形,即,解得.
②当时,四边形是平行四边形,即,解得.
所以当直线将四边形截出一个平行四边形时,点运动了2秒或3秒,
故选B.
13.28或32或36
解:∵∠C=90°,AC=6,BC=8,
∴AB==10,
若以AC,BC为边,则平行四边形的周长=2(AC+BC)=2×(6+8)=28,
若以AC,AB为边,则平行四边形的周长=2(AC+AB)=2×(6+10)=32,
若以AB,BC为边,则平行四边形的周长=2(AB+BC)=2×(10+8)=36,
综上,此平行四边形的周长为28或32或36.
故答案为:28或32或36.
14.3
解:∵四边形ABCD是平行四边形,
∴,AB=CD,
∵,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴AB=DE=CD,即D为CE中点,
∵EF⊥BC,
∴∠EFC=90°,
∵∠BAD=120°,
∴∠BCD=120°,
∴∠ECF=60°,∠CEF=30°,
故设CE=2x,CF=x,在Rt△CEF有:
,
解得x=3,
∴CE=6,
∴,
故答案为:3.
15.2
解:∵四边形ABCD是平行四边形,
∴,
∵AC+BD=12cm,
∴,
∵△OAB的周长是10cm,
∴OA+OB+AB=10cm,
∴AB=4cm,
∵点E、F分别是线段AO,BO的中点,
∴,
故答案为:2
16.3
解:连接DP,
∵∠C=90°,BC=3,CD=3,
∴,
∵点E、点F分别为线段AD、AP的中点,
∴,
当DP最大时,EF长度最大,即当点P与点B重合时,DP有最大值,此时DP=BD=6,
∴EF=3,
故答案为:3.
.
17.
解:过点A作且,连接MP,
∴四边形是平行四边形,
∴,
将的最小值转化为的最小值,当M、P、C三点共线时,的最小,
∵,,
∴,
在中,;
故答案是:.
18.16
解:,
,四边形为平行四边形
,
四边形的周长.
19.证明见解析
证明:由题意知 ,
∴∠ODF=∠OBE
在△DOF和△BOE中
∵
∴△DOF≌△BOE(AAS)
∴DF=BE
∴AD﹣DF=BC﹣BE
即AF=EC
∴四边形AECF为平行四边形.
20.(1)见解析
(2)2
(1)
证明:∵,
∴,
∴∥,
∴,
∵E是边CD的中点,
∴CE=DE,
在△BEC与△FED中,
∴△BEC≌△FED(AAS),
∴,
∴四边形BDFC是平行四边形;
(2)
解:∵BD=BC=3,∠A=90°,,
∴
∵四边形是平行四边形
∴
∴
∴
21.(1)见解析;
(2)直角三角形.
(1)
证明:∵AD//BC,
∴∠ADE=∠BFE,
∵E为AB的中点,
∴AE=BE,
在△ADE和△BFE中,
∴△ADE≌△BFE(AAS),
∴AD=BF;
(2)
解:△FDC是直角三角形,理由如下:
连接EG,
∵∠GDF=∠ADE,∠ADE=∠BFE,
∴∠GDF=∠BFE,
由(1)△ADE≌△BFE得:DE=FE,
即GE为DF上的中线,
∴GE⊥DF,
∵点G是FC的中点,DE=FE,
∴GE//CD,
∴CD⊥DF,
∴△FDC是直角三角形.
22.(1)证明见解析
(2)EF=4
(1)
证明:由题意知,,,AB为△EMN的中位线
∴,
∴
∴,
∴四边形MFCD为平行四边形;
(2)
解:如图,连接AF,BF,则AF是△MNE的中位线
∴AF∥EB,AF=EB
∴四边形AFBE是平行四边形
∴OF=OE=2
∴EF=4.
23.(1)证明见解析;
(2)证明见解析.
解:(1)
∵为平行四边形,
∴, ,,
∴,
,
∴,
∴,
在和中,
,
∴.
(2)
∵是平行四边形,
∴,
∵,
∴,
∴,
∴四边形是平行四边形,
∴.
答案第1页,共2页
一、单选题
1.下面给出的是四边形ABCD中,AB,BC,CD,DA的长度之比,其中能满足四边形ABCD是平行四边形的是( )
A.1:2:3:4 B.2:2:3:3 C.2:3:2:3 D.2:3:3:2
2.下列条件中,能判定四边形是平行四边形的是( )
A.一组对边相等,另一组对边平行 B.对角线互相垂直
C.一组对边相等,一组对角相等 D.一组对边平行,一组对角相等
3. ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AF∥CE C.CE=AF D.∠DAF=∠BCE
4.如图,中,点D、E、F分别为边的中点,则下列关于线段和之间关系的说法中正确的是( )
A. B.
C.和互相平分 D.以上答案都不对
5.如图,已知在中,,,分别是边,,的中点,,,则四边形AFDE的周长等于( )
A.18 B.16 C.14 D.12
6.如图,已知四边形ABCD和四边形BCEF均为平行四边形,∠D=60°,连接AF,并延长交BE于点P,若AP⊥BE,AB=3,BC=2,AF=1,则BE的长为( )
A.5 B.2 C.2 D.3
7.如图,在△ABC中,F为BC的中点,点E是AC边上的一点,且AC=10,当AE的长为( )时,EF∥AB
A.3 B.4 C.5 D.4.5
8.如图,在平行四边形中,为对角线,点是的中点,且,,四边形的周长为10,则平行四边形的周长为( )
A.10 B.12 C.15 D.20
9.如图,某花木场有一块如四边形形状的空地,其中,其各边中点分别是E、F、G、H,测得对角线,现想利用篱笆围成四边形场地,则需篱笆的总长度是( )
A. B. C. D.
10.如图,中,,则图中的平行四边形的个数共有( )
A.7个 B.8个 C.9个 D.11个
11.如图,为测量BC两地的距离,小明在池塘外取点A,得到线段AB,AC,并取AB,AC的中点D,E,连结DE.测得DE的长为6米,则B,C两地相距( )
A.9米 B.10米 C.11米 D.12米
12.如图,在四边形中,,,,点在边上以每秒的速度从点向点运动,点在边上,以每秒的速度从点向点运动,当直线在四边形内部截出一个平行四边形时,点运动了( )
A.2秒 B.2秒或3秒 C.2秒或4秒 D.4秒
二、填空题
13.在△ABC中,∠C=90°,AC=6,BC=8,若以A,B,C,D为顶点的四边形是平行四边形,则此平行四边形的周长为______.
14.如图,平行四边形ABCD中,∠BAD=120°,E、F分别在CD和BC的延长线上,,EF⊥BC,,则AB的长是______.
15.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E、F分别是线段AO,BO的中点,若AC+BD=12cm,△OAB的周长是10cm,则EF=______cm.
16.如图,四边形ABCD中,∠C=90°,BC=3,CD=3,点P为线段BC上的动点,点E、点F分别为线段AD、AP的中点,则EF长度的最大值为 ___.
17.如图,在 ABCD中,点E是对角线AC上一点,过点E作AC的垂线,交边AD于点P,交边BC于点Q,连接PC、AQ,若AC=6,PQ=4,则PC+AQ的最小值为________________.
三、解答题
18.如图,在中,,点,,分别在边,,上, ,,.求四边形的周长.
19.已知:如图,在 ABCD中,E,F分别为BC和AD上的点,BD和EF相交于点O,且OE=OF.求证:四边形AECF为平行四边形.
20.如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长与AD的延长线交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若BC=BD,求BF的长.
21.如图,AD∥BC,点E是AB的中点,联结DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:AD=BF;
(2)当点G是FC的中点时,判断△FDC的形状.
22.点E是 ABCD的边CD上的一点,连接EA并延长,使EA=AM,连接EB并延长,使EB=BN,连接MN,F为MN的中点,连接CF,DM.
(1)求证:四边形DMFC是平行四边形;
(2)连接EF,交AB于点O,若OF=2,求EF的长.
23.已知,如图在中,对角线和相交于点,点,分别在,上,且,连接,.
(1)如图1,求证:;
(2)如图2,延长交于点,延长交于点.求证:.
试卷第1页,共3页
参考答案:
1.C
解:A、,则不能判定是平行四边形,故本选项不符合题意;
B、,则不能判定是平行四边形,故本选项不符合题意;
C、,根据两组对边分别相等的四边形是平行四边形,则能判定是平行四边形,故本选项符合题意;
D、,则不能判定是平行四边形,故本选项不符合题意;
故选:C
2.D
解:A、一组对边相等,另一组对边平行的四边形是等腰梯形,不一定是平行四边形,故选项不符合题意;
B、对角线互相垂直的四边形不一定是平行四边形,故选项不符合题意;
C、由一组邻边相等,一组对角相等,不能判定一个四边形是平行四边形,故选项不符合题意;
D、一组对角相等,一组对边平行,可得到任意两对邻角互补,那么可得到两组对边分别平行,为平行四边形,故选项符合题意;
故选D.
3.C
解:如图,连接AC与BD相交于O,
在 ABCD中,OA=OC,OB=OD,要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项不符合题意;
B、AF∥CE能够利用“角角边”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意;
C、若CE=AF,则无法判断OE=OE,故本选项符合题意;
D、由∠DAF=∠BCE,从而可得△DAF≌△BCE,然后得出∠DFA=∠BEC,
∴∠AFE=∠CEF,
∴AF∥CE,
结合选项B可证明四边形AECF是平行四边形,故本选项不符合题意;
故选:C.
4.C
解:如图,连接FD,ED,
∵,点D、E、F分别为边BC、CA、AB的中点,
∴DE,DF,EF都是△ABC的中位线,
∴DF∥AC,DE∥AB,
∴四边形AEDF是平行四边形,
∴EF与AD互相平分,故C符合题意,D不符合题意;
根据现有条件,无法推出AD=EF,AD⊥EF,故A、B不符合题意,
故选C.
5.A
解:∵D,E,F分别是边BC,CA,AB的中点.AB=10,AC=8,
∴DE=AB=5,DF=AC=4,AF=AB=5,AE=AC=4,
∴四边形AFDE的周长=AF+DF+DE+AE=5+5+4+4=18,
故选:A.
6.D
解:过点D作DH⊥BC,交BC的延长线于点H,连接BD,DE,
∵四边形ABCD是平行四边形,AB=3,∠ADC=60 ,
∴CD=AB=3,∠DCH=∠ABC=∠ADC=60 ,
∵DH⊥BC,
∴∠DHC=90 ,∴∠ADC+∠CDH=90°,∴∠CDH=30°,
在Rt△DCH中,CH=CD=,DH=,
∴,
∵四边形BCEF是平行四边形,
∴AD=BC=EF,AD∥EF,
∴四边形ADEF是平行四边形,
∴AF∥DE,AF=DE=1,
∵AF⊥BE,
∴DE⊥BE,
∴,
∴,
故选D.
7.C
解:当为的中点时,∵F为BC的中点
∴为的中位线,
∴
此时
故选C
8.D
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵点O是BD的中点,且AD//EO,OF//AB,
∴OE,OF分别是三角形ABD,三角形BCD的中位线,BC//EO,
∴四边形OEBF是平行四边形,AD=2OE,CD=2OF,OE=BF,OF=BE,
∵四边形OEBF的周长为10,
∴OE+BE+BF+OF=10,
∴OE+OF=5,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴四边形ABCD的周长=AB+BC+AD+CD=2(AD+CD)=4(OE+OF)=20,
故选D.
9.C
解:过点A作AM∥DC交BC于点M,连接BD
则∠DCB=∠AMB
∵∠DCB=∠ABC
∴∠AMB=∠ABC
∴AM=AB
∵AD∥BC,AM∥DC
∴四边形AMCD是平行四边形
∴AM=DC
∴AB=DC
在△ABC与△DCB中
∴△ABC≌△DCB(SAS)
∴BD=AC=10m
∵E、F、G、H分别为AB、BC、CD、AD的中点
∴GH=EF=,EH=FG=
∴四边形EFGH是平行四边形
则篱笆的总长度为2(GH+EH)=20(m)
故选:C.
10.C
解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,
则图中的四边形AEOG、ABHG、AEFD、ABCD、
GOFD、GHCD、EBHO、EBCF和OHCF都是平行四边形,
共9个,
故选:C.
11.D
解:∵点D,E分别为AB,AC的中点,
∴DE是△ABC的中位线,
∴DE=BC,
∴BC=2DE=2×6=12(米),
故选:D.
12.B
解:设点、运动的时间为秒,依题意得,
,,,,
①当时,四边形是平行四边形,即,解得.
②当时,四边形是平行四边形,即,解得.
所以当直线将四边形截出一个平行四边形时,点运动了2秒或3秒,
故选B.
13.28或32或36
解:∵∠C=90°,AC=6,BC=8,
∴AB==10,
若以AC,BC为边,则平行四边形的周长=2(AC+BC)=2×(6+8)=28,
若以AC,AB为边,则平行四边形的周长=2(AC+AB)=2×(6+10)=32,
若以AB,BC为边,则平行四边形的周长=2(AB+BC)=2×(10+8)=36,
综上,此平行四边形的周长为28或32或36.
故答案为:28或32或36.
14.3
解:∵四边形ABCD是平行四边形,
∴,AB=CD,
∵,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴AB=DE=CD,即D为CE中点,
∵EF⊥BC,
∴∠EFC=90°,
∵∠BAD=120°,
∴∠BCD=120°,
∴∠ECF=60°,∠CEF=30°,
故设CE=2x,CF=x,在Rt△CEF有:
,
解得x=3,
∴CE=6,
∴,
故答案为:3.
15.2
解:∵四边形ABCD是平行四边形,
∴,
∵AC+BD=12cm,
∴,
∵△OAB的周长是10cm,
∴OA+OB+AB=10cm,
∴AB=4cm,
∵点E、F分别是线段AO,BO的中点,
∴,
故答案为:2
16.3
解:连接DP,
∵∠C=90°,BC=3,CD=3,
∴,
∵点E、点F分别为线段AD、AP的中点,
∴,
当DP最大时,EF长度最大,即当点P与点B重合时,DP有最大值,此时DP=BD=6,
∴EF=3,
故答案为:3.
.
17.
解:过点A作且,连接MP,
∴四边形是平行四边形,
∴,
将的最小值转化为的最小值,当M、P、C三点共线时,的最小,
∵,,
∴,
在中,;
故答案是:.
18.16
解:,
,四边形为平行四边形
,
四边形的周长.
19.证明见解析
证明:由题意知 ,
∴∠ODF=∠OBE
在△DOF和△BOE中
∵
∴△DOF≌△BOE(AAS)
∴DF=BE
∴AD﹣DF=BC﹣BE
即AF=EC
∴四边形AECF为平行四边形.
20.(1)见解析
(2)2
(1)
证明:∵,
∴,
∴∥,
∴,
∵E是边CD的中点,
∴CE=DE,
在△BEC与△FED中,
∴△BEC≌△FED(AAS),
∴,
∴四边形BDFC是平行四边形;
(2)
解:∵BD=BC=3,∠A=90°,,
∴
∵四边形是平行四边形
∴
∴
∴
21.(1)见解析;
(2)直角三角形.
(1)
证明:∵AD//BC,
∴∠ADE=∠BFE,
∵E为AB的中点,
∴AE=BE,
在△ADE和△BFE中,
∴△ADE≌△BFE(AAS),
∴AD=BF;
(2)
解:△FDC是直角三角形,理由如下:
连接EG,
∵∠GDF=∠ADE,∠ADE=∠BFE,
∴∠GDF=∠BFE,
由(1)△ADE≌△BFE得:DE=FE,
即GE为DF上的中线,
∴GE⊥DF,
∵点G是FC的中点,DE=FE,
∴GE//CD,
∴CD⊥DF,
∴△FDC是直角三角形.
22.(1)证明见解析
(2)EF=4
(1)
证明:由题意知,,,AB为△EMN的中位线
∴,
∴
∴,
∴四边形MFCD为平行四边形;
(2)
解:如图,连接AF,BF,则AF是△MNE的中位线
∴AF∥EB,AF=EB
∴四边形AFBE是平行四边形
∴OF=OE=2
∴EF=4.
23.(1)证明见解析;
(2)证明见解析.
解:(1)
∵为平行四边形,
∴, ,,
∴,
,
∴,
∴,
在和中,
,
∴.
(2)
∵是平行四边形,
∴,
∵,
∴,
∴,
∴四边形是平行四边形,
∴.
答案第1页,共2页
