1.3 第1课时 同底数幂的除法 课件(共24张PPT)
文档属性
| 名称 | 1.3 第1课时 同底数幂的除法 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 14:22:08 | ||
图片预览







文档简介
(共24张PPT)
BS七(上)
教学课件
第一章 整式的乘除
1.3 同底数幂的除法
第一课时 同底数幂的除法
1.经历同底数幂的除法法则的探索过程,理解同底
数幂的除法法则;
2.理解零次幂和负整数指数幂的意义,并能进行负
整数指数幂的运算;(重点,难点)
3.会用同底数幂的除法法则进行计算.(重点、难点)
学习目标
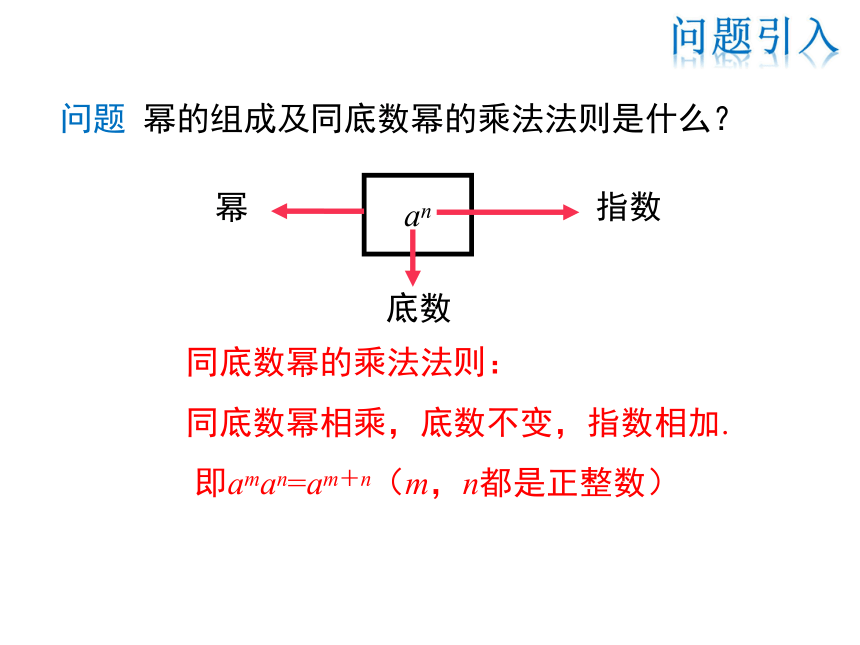
问题 幂的组成及同底数幂的乘法法则是什么?
同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加.
即aman=am+n(m,n都是正整数)
an
底数
幂
指数
一种液体每升含有1012个有害细菌,为了试验某种杀菌剂的效果,科学家们进行了实验,发现1滴杀菌剂可以杀死109个此种细菌.要将1升液体中的有害细菌全部杀死,需要这种杀菌剂多少滴?
1012÷109
(2)观察这个算式,它有何特点?
我们观察可以发现,1012 和109这两个幂的底数相同,是同底的幂的形式.所以我们把1012 ÷109这种运算叫作同底数幂的除法.
(1)怎样列式?
根据同底数幂的乘法法则进行计算:
28×27= 52×53=
a2×a5= 3m-n×3n=
215
55
a7
3m
( )× 27=215
( )×53= 55
( )×a5=a7
( )×3n =
28
a2
52
乘法与除法互为逆运算
215÷27=( )
=215-7
55÷53=( )
=55-3
a7÷a5=( )
=a7-5
3m÷3m-n=( )
=3m-(m-n)
28
52
a2
3n
填一填:
上述运算你发现了什么规律吗?
3m-n
3m
1
同底数幂的除法
猜想:am÷an=am-n(m>n)
验证:am÷an=
m个a
n个a
=(a·a· ··· ·a)
m-n个a
=am-n
(a≠0,m,n是正整数,且m>n).
am÷an=am-n
即:同底数幂相除,底数不变,指数相减.
计算:
(1)a7÷a4; (2)(-x)6÷(-x)3;
(3)(xy)4÷(xy); (4)b2m+2÷b2.
(1)a7÷a4=a7-4
=(-x)3
(3)(xy)4÷(xy)=(xy)4-1
(4)b2m+2÷b2
注意:同底数幂相除,底数不变,指数相减.
解:
=a3;
(2)(-x)6÷(-x)3=(-x)6-3
=-x3;
=(xy)3
=x3y3;
=b2m+2-2
=b2m.
例1
已知:am=8,an=5. 求:
(1)am-n的值; (2)a3m-3n的值.
解:(1)am-n=am÷an=8÷5 = 1.6;
(2)a3m-3n= a3m ÷ a3n
= (am)3 ÷(an)3
=83 ÷53
=512 ÷125
=
同底数幂的除法可以逆用:am-n=am÷an
这种思维叫作逆向思维 (逆用运算性质).
3
2
1
0
–1
–2
–3
3
2
1
0
–1
–2
–3
2
零次幂与负整数次幂
我们规定
即任何不等于零的数的零次幂都等于1.
即用a-n表示an的倒数.
用小数或分数表示下列各数:
解:
(1)10-3; (2)70×8-2; (3)1.6×10-4.
(1)10-3
=0.001.
(2)70×8-2
注意:a0 =1
(3)1.6×10-4
=1.6×0.0001
=0.00016.
例2
计算下列各式,你有什么发现?与同伴交流.
(1)7-3÷7-5;
(2)3-1÷36;
(3)(-8)0÷(-8)-2.
解:(1)7-3÷7-5=
=7-3-(-5);
(2)3-1÷36=
=3-1-6
(3)(-8)0÷(-8)-2=
=(-8)0-(-2)
练一练
(a≠0,m,n是任意整数).
1.am÷an=am-n
即:同底数幂相除,底数不变,指数相减.
1.计算:
2.计算(结果用整数或分数表示):
1
1
64
3.下面的计算对不对?如果不对,请改正.
4.已知3m=2, 9n=10, 求33m-2n 的值.
解: 33m-2n =33m÷32n
=(3m)3÷(32)n
=(3m)3÷9n
=23÷10
=8÷10
=0.8.
5. 地震的强度通常用里克特震级表示,描绘地震级数
字表示地震的强度是10的若干次幂.例如,用里克特
震级表示地震是8级,说明地震的强度是107.1992年
4月,荷兰发生了5级地震,12天后,加利福尼亚发
生了7级地震,加利福尼亚的地震强度是荷兰地震
强度的多少倍?
解:由题意得 ,
答:加利福尼亚的地震强度是荷兰地震强度的100倍.
6.若a=(- )-2,b=(-1)-1,c=(- )0,则
a、b、c的大小关系是( )
A.a>b=c B.a>c>b
C.c>a>b D.b>c>a
解析:∵a=(- )-2=(- )2= ,
b=(-1)-1=-1,c=(- )0=1,
∴a>c>b.
B
7.计算:-22+(- )-2+(2016-π)0-|2- π|.
解:-22+(- )-2+(2016-π)0-|2- π|
=-4+4+1-2+ π
= π-1.
1.同底数幂的除法法则:
同底数幂相除, 底数不变,指数相减.
(a≠0, m、n为任意整数)
2.任何不等于零的数的零次幂都等于1.
3.负整数指数幂:
(a≠0,n为正整数)
BS七(上)
教学课件
第一章 整式的乘除
1.3 同底数幂的除法
第一课时 同底数幂的除法
1.经历同底数幂的除法法则的探索过程,理解同底
数幂的除法法则;
2.理解零次幂和负整数指数幂的意义,并能进行负
整数指数幂的运算;(重点,难点)
3.会用同底数幂的除法法则进行计算.(重点、难点)
学习目标
问题 幂的组成及同底数幂的乘法法则是什么?
同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加.
即aman=am+n(m,n都是正整数)
an
底数
幂
指数
一种液体每升含有1012个有害细菌,为了试验某种杀菌剂的效果,科学家们进行了实验,发现1滴杀菌剂可以杀死109个此种细菌.要将1升液体中的有害细菌全部杀死,需要这种杀菌剂多少滴?
1012÷109
(2)观察这个算式,它有何特点?
我们观察可以发现,1012 和109这两个幂的底数相同,是同底的幂的形式.所以我们把1012 ÷109这种运算叫作同底数幂的除法.
(1)怎样列式?
根据同底数幂的乘法法则进行计算:
28×27= 52×53=
a2×a5= 3m-n×3n=
215
55
a7
3m
( )× 27=215
( )×53= 55
( )×a5=a7
( )×3n =
28
a2
52
乘法与除法互为逆运算
215÷27=( )
=215-7
55÷53=( )
=55-3
a7÷a5=( )
=a7-5
3m÷3m-n=( )
=3m-(m-n)
28
52
a2
3n
填一填:
上述运算你发现了什么规律吗?
3m-n
3m
1
同底数幂的除法
猜想:am÷an=am-n(m>n)
验证:am÷an=
m个a
n个a
=(a·a· ··· ·a)
m-n个a
=am-n
(a≠0,m,n是正整数,且m>n).
am÷an=am-n
即:同底数幂相除,底数不变,指数相减.
计算:
(1)a7÷a4; (2)(-x)6÷(-x)3;
(3)(xy)4÷(xy); (4)b2m+2÷b2.
(1)a7÷a4=a7-4
=(-x)3
(3)(xy)4÷(xy)=(xy)4-1
(4)b2m+2÷b2
注意:同底数幂相除,底数不变,指数相减.
解:
=a3;
(2)(-x)6÷(-x)3=(-x)6-3
=-x3;
=(xy)3
=x3y3;
=b2m+2-2
=b2m.
例1
已知:am=8,an=5. 求:
(1)am-n的值; (2)a3m-3n的值.
解:(1)am-n=am÷an=8÷5 = 1.6;
(2)a3m-3n= a3m ÷ a3n
= (am)3 ÷(an)3
=83 ÷53
=512 ÷125
=
同底数幂的除法可以逆用:am-n=am÷an
这种思维叫作逆向思维 (逆用运算性质).
3
2
1
0
–1
–2
–3
3
2
1
0
–1
–2
–3
2
零次幂与负整数次幂
我们规定
即任何不等于零的数的零次幂都等于1.
即用a-n表示an的倒数.
用小数或分数表示下列各数:
解:
(1)10-3; (2)70×8-2; (3)1.6×10-4.
(1)10-3
=0.001.
(2)70×8-2
注意:a0 =1
(3)1.6×10-4
=1.6×0.0001
=0.00016.
例2
计算下列各式,你有什么发现?与同伴交流.
(1)7-3÷7-5;
(2)3-1÷36;
(3)(-8)0÷(-8)-2.
解:(1)7-3÷7-5=
=7-3-(-5);
(2)3-1÷36=
=3-1-6
(3)(-8)0÷(-8)-2=
=(-8)0-(-2)
练一练
(a≠0,m,n是任意整数).
1.am÷an=am-n
即:同底数幂相除,底数不变,指数相减.
1.计算:
2.计算(结果用整数或分数表示):
1
1
64
3.下面的计算对不对?如果不对,请改正.
4.已知3m=2, 9n=10, 求33m-2n 的值.
解: 33m-2n =33m÷32n
=(3m)3÷(32)n
=(3m)3÷9n
=23÷10
=8÷10
=0.8.
5. 地震的强度通常用里克特震级表示,描绘地震级数
字表示地震的强度是10的若干次幂.例如,用里克特
震级表示地震是8级,说明地震的强度是107.1992年
4月,荷兰发生了5级地震,12天后,加利福尼亚发
生了7级地震,加利福尼亚的地震强度是荷兰地震
强度的多少倍?
解:由题意得 ,
答:加利福尼亚的地震强度是荷兰地震强度的100倍.
6.若a=(- )-2,b=(-1)-1,c=(- )0,则
a、b、c的大小关系是( )
A.a>b=c B.a>c>b
C.c>a>b D.b>c>a
解析:∵a=(- )-2=(- )2= ,
b=(-1)-1=-1,c=(- )0=1,
∴a>c>b.
B
7.计算:-22+(- )-2+(2016-π)0-|2- π|.
解:-22+(- )-2+(2016-π)0-|2- π|
=-4+4+1-2+ π
= π-1.
1.同底数幂的除法法则:
同底数幂相除, 底数不变,指数相减.
(a≠0, m、n为任意整数)
2.任何不等于零的数的零次幂都等于1.
3.负整数指数幂:
(a≠0,n为正整数)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
