沪科版七年级数学上册《直线与角》单元测试卷
文档属性
| 名称 | 沪科版七年级数学上册《直线与角》单元测试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 301.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-02 00:00:00 | ||
图片预览




文档简介
七年级数学上册《直线与角》练习题
一.选择题(共10小题,满分40分)
1.有三个点A,B,C,过其中每两个点画直线,可以画出直线( )
A.
1条
B.
2条
C.
1条或3条
D.
无法确定
2.由河源到广州的某一次列车,运行途中停靠的车站依次是:河源﹣惠州﹣东莞﹣广州,那么要为这次列车制作的火车票有( )
A.
3种
B.
4种
C.
6种
D.
12种
3.从哈尔滨开往某市的特快列车,途中要停靠两个站点,如果任意两站间的票价都不同,那么有多少种不同的票价( )
A.
3
B.
4
C.
6
D.
12
4.已知线段AB,在BA的延长线上取一点C,使CA=3AB,则线段CA与线段CB之比为( )
A.
3:4
B.
2:3
C.
3:5
D.
1:2
5.某公司员工分别住在A、B、C三个住宅区,A区有30人,B区有15人,C区有10人.三个区在一条直线上,位置如图所示.公司的接送打算在此间只设一个停靠点,要使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在( )
A.
A区
B.
B区
C.
C区
D.
不确定
6. 4点10分,时针与分针所夹的小于平角的角为( )
A.
55°
B.
65°
C.
70°
D.
以上结论都不对
7.一个角的余角比它的补角的少20°,则这个角为( )
A.
30°
B.
40°
C.
60°
D.
75°
8.将一张纸按如图的方式折叠,BC、BD为折痕,则∠CBD的度数为( )
A.
80°
B.
90°
C.
100°
D.
110°
9.如图,∠AOB=130°,射线OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的平分线,下列叙述正确的是( )
A.
∠DOE的度数不能确定
B.
∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°
C.
∠BOE=2∠COD
D.
∠AOD=
10.已知∠AOB=60°,其角平分线为OM,∠BOC=20°,其角平分线为ON,则∠MON的大小为( )
A.
20°
B.
40°
C.
20°或40°
D.
30°或10°
二.填空题(共10小题,满分40分)
11.已知n(n≥2)个点P1,P2,P3,…,Pn在同一平面内,且其中没有任何三点在同一直线上.设Sn表示过这n个点中的任意2个点所作的所有直线的条数,显然,S2=1,S3=3,S4=6,S5=10,…,由此推断,Sn= _________ .
12.一条直线上有若干个点,以任意两点为端点可以确定一条线段,线段的条数与点的个数之间的对应关系如下表所示.请你探究表内数据间的关系,根据发现的规律,则表中n= _________ .
点的个数
2
3
4
5
6
7
线段的条数
1
3
6
10
15
n
13.已知线段AB=8cm,在直线AB上画线段BC,使它等于3cm,则线段AC= _________ cm.
14.已知AB=8cm,若点C在AB的延长线上,且B为AC的一个三等分点,则AC= _________ cm.
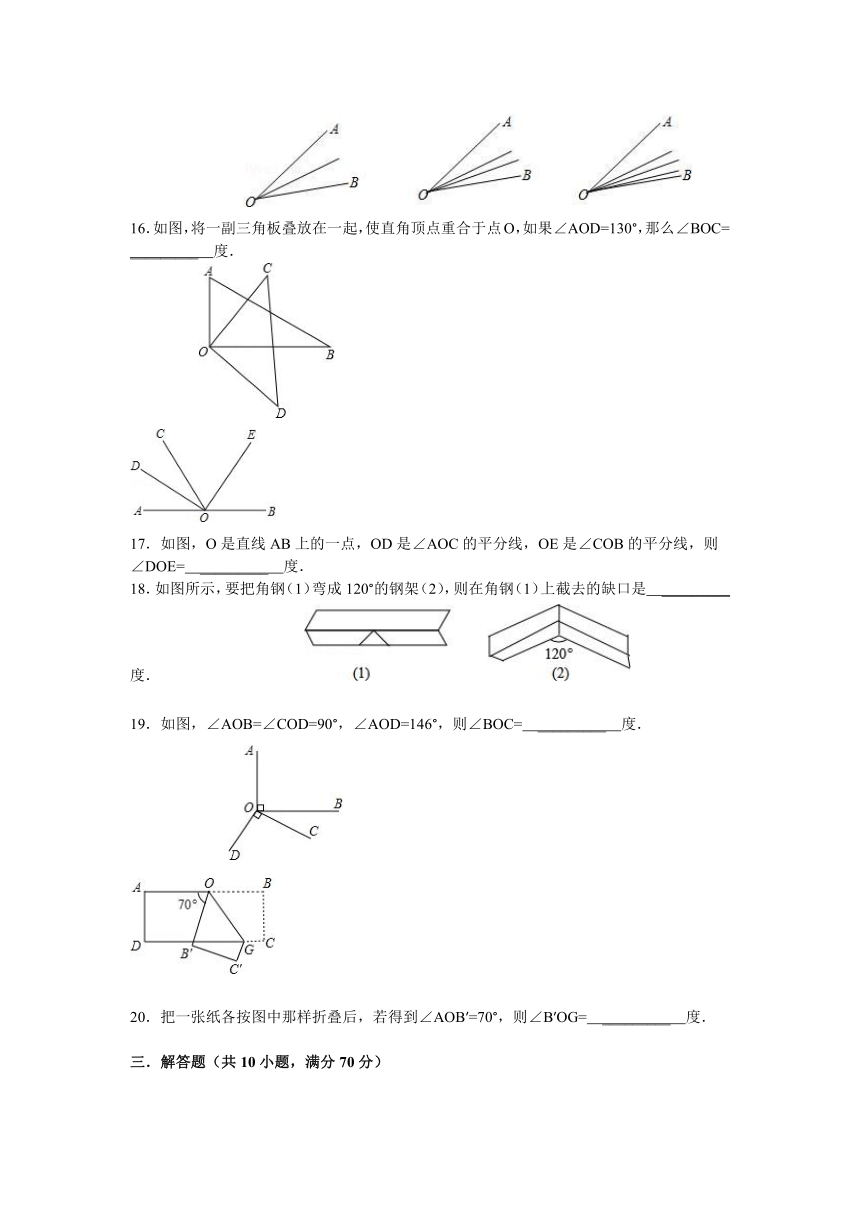
15.在锐角∠AOB内部,画1条射线,可得3个锐角;画2条不同射线,可得6个锐角;画3条不同射线,可得10个锐角;…照此规律,画10条不同射线,可得锐角 _________ 个.
16.如图,将一副三角板叠放在一起,使直角顶点重合于点O,如果∠AOD=130°,那么∠BOC= _________ 度.
17.如图,O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB的平分线,则∠DOE= _________ 度.
18.如图所示,要把角钢(1)弯成120°的钢架(2),则在角钢(1)上截去的缺口是 _________ 度.
19.如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC= _________ 度.
20.把一张纸各按图中那样折叠后,若得到∠AOB′=70°,则∠B′OG= _________ 度.
三.解答题(共10小题,满分70分)
21.考点办公室设在校园中心O点,带队老师休息室A位于O点的北偏东45°,某考室B位于O点南偏东60°,请在图中画出射线OA,OB,并计算∠AOB的度数.
22.已知一个角的补角比这个角的余角的3倍大10°,求这个角的度数.
23.如图是一个正方体的展开图,标注了字母“a”的面是正方体的正面,如果正方体相对两个面上的代数式的值相等,求x、y的值.
24.一个正方体6个面分别写着1、2、3、4、5、6,根据下列摆放的三种情况,那么每个数对面上的数是几?
25.知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.
情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由。
你赞同以上哪种做法?
26.如图,AD=DB,E是BC的中点,BE=AC=2cm,求线段DE的长.
27.如图所示,A,B,C是一条公路上的三个村庄,A,B间路程为100km,A,C间路程为40km,现在A,B之间建一个车站P,设P,C之间的路程为xkm.
(1)用含x的代数式表示车站到三个村庄的路程之和;
(2)若路程之和为102km,则车站应设在何处?
(3)若要使车站到三个村庄的路程总和最小,问车站应设在何处?最小值是多少?
28.如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,求∠AOB的度数.
29.如图所示,设相邻两个角∠AOB,∠BOC的平分线分别为OE,OF,且∠EOF是直角,你能说明OA,OC为什么成一条直线吗?试试看吧!
30.(1)已知∠BOC=120°,∠AOB=70°,求∠AOC的大小;
(2)已知∠AOB=80°,过O作射线OC(不同于OA、OB),满足∠AOC=∠BOC,求∠AOC的大小.
(注:本题中所说的角都是指小于平角的角)
参考答案与试题解析
一.选择题:
1.有三个点A,B,C,过其中每两个点画直线,可以画出直线( )
A.
1条
B.
2条
C.
1条或3条
D.
无法确定
考点:
直线、射线、线段.
分析:
此题考查直线的基本性质:两点确定一条直线.
解答:
解:∵三点在一条直线上能画一条直线,三点不在一条直线上能画三条直线;故选C.
点评:
注意对题目中已知条件的不同情况的分析.
2.由河源到广州的某一次列车,运行途中停靠的车站依次是:河源﹣惠州﹣东莞﹣广州,那么要为这次列车制作的火车票有( )
A.
3种
B.
4种
C.
6种
D.
12种
考点:
直线、射线、线段.
专题:
应用题.
分析:
由题意可知:由河源要经过3个地方,所以要制作3种车票;由惠州要经过2个地方,所以要制作2种车票;由东莞要经过1个地方,所要制作1种车票;结合上述结论,通过往返计算出答案.
解答:
解:根据分析,知
这次列车制作的火车票的总数=(3+2+1)×2=12(种).
故选D.
点评:
本题的关键是要找出由一地到另一地的车票的数是多少.
3.从哈尔滨开往某市的特快列车,途中要停靠两个站点,如果任意两站间的票价都不同,那么有多少种不同的票价( )
A.
3
B.
4
C.
6
D.
12
考点:
直线、射线、线段.
专题:
计算题;应用题.
分析:
由题意可知:由哈尔滨到某市要经过2个站点,则在哈尔滨车票的票价有3种.
依此类推,在第一个站点的票价有2种.
在第二个站点的票价有1种,从而求得总结果数.
解答:
解:根据分析,得
共有票价3+2+1=6(种).
故选C.
点评:
本题的关键是要理解由一地到另一地的车票的票价都是不同的.
4.已知线段AB,在BA的延长线上取一点C,使CA=3AB,则线段CA与线段CB之比为( )
A.
3:4
B.
2:3
C.
3:5
D.
1:2
考点:
比较线段的长短.
分析:
根据题意,画出图形,因为CA=3AB,则CB=CA+AB=4AB,故线段CA与线段CB之比可求.
解答:
解:如上图所示
∵CA=3AB
∴CB=CA+AB=4AB
∴CA:CB=3:4.
故选A.
点评:
在未画图类问题中,正确画图很重要.灵活运用线段的和、差、倍、分转化线段之间的数量关系十分关键.
5.某公司员工分别住在A、B、C三个住宅区,A区有30人,B区有15人,C区有10人.三个区在一条直线上,位置如图所示.公司的接送打算在此间只设一个停靠点,要使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在( )
A.
A区
B.
B区
C.
C区
D.
不确定
考点:
比较线段的长短.
分析:
根据题意分别计算停靠点分别在各点是员工步行的路程和,选择最小的即可解
解答:
解:∵当停靠点在A区时,所有员工步行到停靠点路程和是:15×100+10×300=4500m;
当停靠点在B区时,所有员工步行到停靠点路程和是:30×100+10×200=5000m;
当停靠点在C区时,所有员工步行到停靠点路程和是:30×300+15×200=12000m.
∴当停靠点在A区时,所有员工步行到停靠点路程和最小,那么停靠点的位置应该在A区.
故选A.
点评:
此题考查了比较线段的长短,正确理解题意是解题的关键.要能把线段的概念在现实中进行应用.
6. 4点10分,时针与分针所夹的小于平角的角为( )
A.
55°
B.
65°
C.
70°
D.
以上结论都不对
考点:
钟面角.
分析:
因为钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,找出4点10分时针和分针分别转动角度即可求出.
解答:
解:∵4点10分时,分针从12到2转动两个格转动角度为:30°×2=60°,时针转动×30°=5°,
∴4点10分时,分针与时针的夹角是2×30°+5°=65°.
故选:B.
点评:
本题考查钟表时针与分针的夹角.用到的知识点为:钟表上12个数字,每相邻两个数字之间的夹角为30°.
7.一个角的余角比它的补角的少20°,则这个角为( )
A.
30°
B.
40°
C.
60°
D.
75°
考点:
余角和补角.
专题:
计算题.
分析:
因为一个角的余角比它的补角的少20,
所以不妨设这个角为α,则它的余角为β=90°﹣∠α,补角γ=为180°﹣∠α,且β=﹣20°,化简即可得出答案.
解答:
解:设这个角为α,则它的余角为β=90°﹣∠α,补角γ=为180°﹣∠α,且β=﹣20°
即90°﹣∠α=(180°﹣∠α)﹣20°
∴2(90°﹣∠α+20°)=180°﹣∠α
∴180°﹣2∠α+40°=180°﹣∠α
∴∠α=40°.
故选B.
点评:
此题考查的是角的性质,两角互余和为90°,互补和为180°,也考查了对题意的理解,可结合换元法来解题.
8.将一张纸按如图的方式折叠,BC、BD为折痕,则∠CBD的度数为( )
A.
80°
B.
90°
C.
100°
D.
110°
考点:
角的计算.
专题:
计算题.
分析:
根据折叠前后两图形是全等形,其角不变来解决.
解答:
解:∵折叠前后两图形是全等形,
∴∠CBD=180°×=90°.
故选B.
点评:
这是一个折叠问题,要善于发现题中的隐含条件:折叠前后两图形是全等形,其角不变.
9.如图,∠AOB=130°,射线OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的平分线,下列叙述正确的是( )
A.
∠DOE的度数不能确定
B.
∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°
C.
∠BOE=2∠COD
D.
∠AOD=
考点:
角平分线的定义.
分析:
本题是对角的平分线的性质的考查,角平分线将角分成相等的两部分.结合选项得出正确结论.
解答:
解:∵OD、OE分别是∠AOC、∠BOC的平分线,
∴∠AOD=∠COD、∠EOC=∠BOE,
又∵∠AOD+∠BOE+∠EOC+∠COD=∠AOB=130°,
∴∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°.
故选B.
点评:
本题是对角平分线的性质的考查.然后根据角平分线定义得出所求角与已知角的关系转化求解.
10.已知∠AOB=60°,其角平分线为OM,∠BOC=20°,其角平分线为ON,则∠MON的大小为( )
A.
20°
B.
40°
C.
20°或40°
D.
30°或10°
考点:
角平分线的定义.
专题:
分类讨论.
分析:
根据题意,画出图形,分两种情况讨论:∠BOC在∠AOB内部和外部.
解答:
解:∠BOC在∠AOB内部
∵∠AOB=60°,其角平分线为OM
∴∠MOB=30°
∵∠BOC=20°,其角平分线为ON
∴∠BON=10°
∴∠MON=∠MOB﹣∠BON=30°﹣10°=20°;
∠BOC在∠AOB外部
∵∠AOB=60°,其角平分线为OM
∴∠MOB=30°
∵∠BOC=20°,其角平分线为ON
∴∠BON=10°
∴∠MON=∠MOB+∠BON=30°+10°=40°.
故选C.
点评:
本题主要考查平分线的性质,知道∠BOC在∠AOB内部和外部两种情况是解题的关键.
二.填空题
11.已知n(n≥2)个点P1,P2,P3,…,Pn在同一平面内,且其中没有任何三点在同一直线上.设Sn表示过这n个点中的任意2个点所作的所有直线的条数,显然,S2=1,S3=3,S4=6,S5=10,…,由此推断,Sn= .
考点:
直线、射线、线段.
专题:
规律型.
分析:
分析数据后总结规律,再进行计算.
解答:
解:∵S2=1=,
S3=3=1+2=,
S4=6=1+2+3=,
∴Sn=1+2+3+…+(n﹣1)=.
点评:
本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
12.一条直线上有若干个点,以任意两点为端点可以确定一条线段,线段的条数与点的个数之间的对应关系如下表所示.请你探究表内数据间的关系,根据发现的规律,则表中n= 21 .
点的个数
2
3
4
5
6
7
线段的条数
1
3
6
10
15
n
考点:
直线、射线、线段.
专题:
规律型.
分析:
根据表中数据,寻找规律,列出公式解答.
解答:
解:设线段有n个点,分成的线段有m条.有以下规律:
n个m条
2 1
3 1+2
4 1+2+3
…
n m=1+…+(n﹣1)
=
7个点把线段AB共分成=21条.
点评:
本题体现了“具体﹣﹣﹣抽象﹣﹣﹣﹣具体”的思维探索过程,探索规律、运用规律,有利于培养学生健全的思维能力.
13.已知线段AB=8cm,在直线AB上画线段BC,使它等于3cm,则线段AC= 5或11 cm.
考点:
两点间的距离.
专题:
分类讨论.
分析:
点C可能在线段BC上,也可能在BC的延长线上.因此分类讨论计算.
解答:
解:根据题意,点C可能在线段BC上,也可能在BC的延长线上.
若点C在线段BC上,则AC=AB﹣BC=8﹣3=5(cm);
若点C在BC的延长线上,则AC=AB+BC=8+3=11(cm).
故答案为 5或11.
点评:
此题考查求两点间的距离,运用了分类讨论的思想,容易掉解.
14.已知AB=8cm,若点C在AB的延长线上,且B为AC的一个三等分点,则AC= 12或24 cm.
考点:
比较线段的长短.
专题:
分类讨论.
分析:
已知AB的长度,根据B为AC的一个三等分点,因B点不确定,要分类讨论.
解答:
解:本题要分两种情况讨论:
①如果,BC占线段AC的三分之一,则AC等于12cm;
②如果AB占线段AC的三分之一,AC等于24cm.
∴AC=12或24cm.
点评:
要分类讨论,以确定AC的长度.
15.在锐角∠AOB内部,画1条射线,可得3个锐角;画2条不同射线,可得6个锐角;画3条不同射线,可得10个锐角;…照此规律,画10条不同射线,可得锐角 66 个.
考点:
角的概念.
专题:
规律型.
分析:
分别找出各图形中锐角的个数,找出规律解题.
解答:
解:∵在锐角∠AOB内部,画1条射线,可得1+2=3个锐角;
在锐角∠AOB内部,画2条射线,可得1+2+3=6个锐角;
在锐角∠AOB内部,画3条射线,可得1+2+3+4=10个锐角;
…
∴从一个角的内部引出n条射线所得到的锐角的个数是
1+2+3+…+(n+1)=×(n+1)×(n+2),
∴画10条不同射线,可得锐角×(10+1)×(10+2)=66.
点评:
从一个角的内部引出n条射线所得到的锐角的个数是×(n+1)×(n+2).
16.如图,将一副三角板叠放在一起,使直角顶点重合于点O,如果∠AOD=130°,那么∠BOC= 50 度.
考点:
角的计算.
专题:
计算题.
分析:
根据图示确定∠BOC与两个直角的关系,它等于两直角的和减去∠AOD的度数.
解答:
解:∠BOC=∠COD+∠AOB﹣∠AOD=90°+90°﹣130°=50°.
故填50.
点评:
首先确定这几个角之间的关系,来求出∠BOD的度数.
17.如图,O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB的平分线,则∠DOE= 90 度.
考点:
角平分线的定义.
专题:
计算题.
分析:
利用角平分线的性质和平角的定义计算.
解答:
解:∵OD是∠AOC的平分线∴∠AOD=∠DOC
∵OE是∠COB的平分线∴∠COE=∠EOB
∴∠AOD+∠EOB=∠DOC+∠COE
∵∠AOD+∠DOC+∠COE+∠EOB=180°
∴2(∠DOC+∠COE)=180°
即∠DOE=90°.
故填90.
点评:
熟记平角的特点与角平分线的性质是解决此题的关键.
18.如图所示,要把角钢(1)弯成120°的钢架(2),则在角钢(1)上截去的缺口是 60 度.
考点:
角的计算.
专题:
计算题.
分析:
本题是平角的定义及角的应用的考查.因为在截取之前的角是平角180°,截完弯折后左右两边重合,所组成的新角是120°,所以缺口角易求.
解答:
解:因为缺口角加120°,在截取之前的角是平角180°,所以缺口角等于180°﹣120°=60度.故答案为60.
点评:
本题是实际应用题,截取弯成后的角与缺口角是互补的,理解这个问题是解题的关键.
19.如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC= 34 度.
考点:
角的计算.
专题:
计算题.
分析:
根据周角的定义,1周角=360°,∠AOB=∠COD=90°,∠AOD=146°则∠BOC=360°﹣2×90°﹣146°=34°.
解答:
解:∠AOB=∠COD=90°,∠AOD=146°
则∠BOC=360°﹣2×90°﹣146°=34°
则∠BOC=34度.
故答案为34.
点评:
本题主要考查周角的概念.根据已知条件求未知角的度数,是一个比较简单的问题.
20.把一张纸各按图中那样折叠后,若得到∠AOB′=70°,则∠B′OG= 55 度.
考点:
角的计算.
专题:
计算题.
分析:
根据题意∠B′OG=∠BOG,根据平角和角平分线的定义即可求得.
解答:
解:由题意可得∠B′OG=∠BOG,
则∠B′OG=(180﹣∠AOB′)÷2=55°.
故答案为55.
点评:
已知折叠问题就是已知图形全等,因而得到相等的角.
三.解答题
21.考点办公室设在校园中心O点,带队老师休息室A位于O点的北偏东45°,某考室B位于O点南偏东60°,请在图中画出射线OA,OB,并计算∠AOB的度数.
考点:
方向角.
专题:
作图题.
分析:
考查方位角的相关知识,找出中心点,根据题意画出图形.
解答:
解:∵∠1=45°,∠2=60°,
∴∠AOB=180°﹣(45°+60°)=75°.
点评:
掌握好方向角的基本知识,找清楚角度画出图形.
22.已知一个角的补角比这个角的余角的3倍大10°,求这个角的度数.
考点:
余角和补角.
专题:
计算题.
分析:
利用题中“一个角的补角比这个角的余角的3倍大10°”作为相等关系列方程求解即可.
解答:
解:设这个角是x,则(180°﹣x)﹣3(90°﹣x)=10°,
解得x=50°.
故答案为50°.
点评:
主要考查了余角和补角的概念以及运用.互为余角的两角的和为90°,互为补角的两角之和为180度.解此题的关键是能准确的从图中找出角之间的数量关系,从而计算出结果.
23.如图是一个正方体的展开图,标注了字母“a”的面是正方体的正面,如果正方体相对两个面上的代数式的值相等,求x、y的值.
考点:
专题:正方体相对两个面上的文字;二元一次方程的解.
分析:
由平面图形的折叠及立体图形的表面展开图的特点解题.3与a是相对,5﹣x与y+1相对,y与2x﹣5相对.
解答:
解:根据题意,得(4分)
解方程组,得x=3,y=1.(6分)
点评:
注意运用空间想象能力,找出正方体的每个面相对的面
24.一个正方体6个面分别写着1、2、3、4、5、6,根据下列摆放的三种情况,那么每个数对面上的数是几?
考点:
专题:正方体相对两个面上的文字.
分析:
根据正方体的特征知,相邻的面一定不是对面,所以面“1”与面“4”相对,面“2”与面“5”相对,“3”与面“6”相对.
解答:
解:根据正方体的特征知,相邻的面一定不是对面,所以面“1”与面“4”相对,面“2”与面“5”相对,“3”与面“6”相对.1对4,2对5,3对6
点评:
注意正方体的空间图形,从相对面入手,分析及解答问题.
25.知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.
情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:
你赞同以上哪种做法?
考点:
线段的性质:两点之间线段最短.
专题:
作图题;方案型.
分析:
因为教学楼和图书馆处于同一条直线上,两点之间线段最短;连接AB,使AB两点同在一条直线上,与河流的交点既是最佳位置.
解答:
解:情景一:因为教学楼和图书馆处于同一条直线上,两点之间的所有连线中,线段最短;
情景二:(需画出图形,并标明P点位置)
理由:两点之间的所有连线中,线段最短.
赞同情景二中运用知识的做法.
点评:
此题为数学知识的应用,考查知识点两点之间线段最短.
26.如图,AD=DB,E是BC的中点,BE=AC=2cm,求线段DE的长.
考点:
比较线段的长短.
专题:
数形结合.
分析:
根据题目已知条件结合图形可知,要求DE的长可以用AC长减去AD长再减去EC长或者用DB长加上BE长.
解答:
解:由于BE=AC=2cm,则AC=10cm,
∵E是BC的中点,∴BE=EC=2cm,BC=2BE=2×2=4cm,
则AB=AC﹣BC=10﹣4=6cm,
又∵AD=DB,则AB=AD+DB=AD+2AD=3AD=6cm,AD=2cm,DB=4cm,
所以,DE=AC﹣AD﹣EC=10﹣2﹣2=6cm,或DE=DB+BE=4+2=6cm.
故答案为6cm.
点评:
本题考查求线段及线段中点的知识,解这列题要结合图形根据题目所给的条件,寻找所求与已知线段之间的关系,最后求解.
27.如图所示,A,B,C是一条公路上的三个村庄,A,B间路程为100km,A,C间路程为40km,现在A,B之间建一个车站P,设P,C之间的路程为xkm.
(1)用含x的代数式表示车站到三个村庄的路程之和;
(2)若路程之和为102km,则车站应设在何处?
(3)若要使车站到三个村庄的路程总和最小,问车站应设在何处?最小值是多少?
考点:
比较线段的长短.
专题:
计算题.
分析:
(1)由图易得AP=AC+PC,BP=100﹣AP;
(2)让(1)所求得的代数式的值为102,求得x即可;
(3)路程和最小,那么x应最小,此时为0,P与C重合.
解答:
解:(1)路程之和为PA+PC+PB=40+x+100﹣(40+x)+x=(100+x)km;
(2)100+x=102,x=2,车站在C两侧2km处;
(3)当x=0时,x+100=100,小站建在C处路程和最小,路程和为100km.
点评:
读懂题意,找到所求量的等量关系是解决本题的关键.
28.如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,求∠AOB的度数.
考点:
角平分线的定义.
分析:
此题可以设∠AOB=x,∠BOC=2x,再进一步表示∠AOC=3x,根据角平分线的概念表示∠AOD,最后根据已知角的度数列方程即可计算.
解答:
解:设∠AOB=x,∠BOC=2x.则∠AOC=3x.
又OD平分∠AOC,
∴∠AOD=.
∴∠BOD=∠AOD﹣∠AOB=﹣x=14°
∴x=28°
即∠AOB=28°.
故答案为28°.
点评:
此类题设恰当的未知数,根据已知条件进一步表示出相关的角,列方程计算较为简便.
29.如图所示,设相邻两个角∠AOB,∠BOC的平分线分别为OE,OF,且∠EOF是直角,你能说明OA,OC为什么成一条直线吗?试试看吧!
考点:
角平分线的定义.
分析:
判断OA,OC是否成一条直线,只要求∠AOC,看是否是180°.
解答:
解:∵OE、OF分别平分∠AOB、∠BOC,且∠EOF是直角,
∴∠AOE=∠BOE,∠COF=∠BOF,∠EOF=90°,
∴(∠AOE+∠EOB)+(∠COF+∠BOF)=2×90°=180°,
即∠AOB+∠BOC=180°,
∴∠AOC=180°,
∴AO、OC成一直线(即A,O,C三点共线).
点评:
判断A,O,C三点共线的方法就是转化为求∠AOC的度数.
30.(1)已知∠BOC=120°,∠AOB=70°,求∠AOC的大小;
(2)已知∠AOB=80°,过O作射线OC(不同于OA、OB),满足∠AOC=∠BOC,求∠AOC的大小.
(注:本题中所说的角都是指小于平角的角)
考点:
角的计算.
专题:
分类讨论.
分析:
(1)是角的多解问题,求解时因为位置不同,可分情况讨论.
(2)直线OA、OB将平面分成四个部分,分别考虑射线OC落在这四个部分的情况,
解答:
解:(1)当射线OA在∠COB内部时,
因为∠AOB=70°,∠BOC=120°,
所以∠AOC=∠BOC﹣∠AOB=120°﹣70°=50°
当射线OA在∠COB外部时,
因为∠AOB=70°,∠BOC=120°,
所以∠AOC=∠BOC+∠AOB=120°+70°=190°,
而求解的只是小于平角的角,
所以∠AOC=∠=360°﹣190°=170°
所以∠AOC等于50°或170°.
(2)根据题意画出图形得:
∵∠AOB=80°,∠AOC=∠BOC,
∴设∠BOC=5x,则∠AOC=3x,根据题意列出方程得:5x+3x=80°,
解得x=10°
∴∠AOC=30°,∠BOC=50°;
∵∠AOB=80°,∠AOC=∠BOC,
∴设∠BOC=5x,则∠AOC=3x,根据题意列出方程得:5x+3x=280°,
解得x=35°
∴∠AOC=105°,∠BOC=175°.
点评:
本题的多解情况可依据不同情况求解,在计算中我们所求的角一般都是小于平角的角.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
