六年级下册数学课件 - 3.2反比例的意义 西师大版(12张PPT)
文档属性
| 名称 | 六年级下册数学课件 - 3.2反比例的意义 西师大版(12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 09:43:40 | ||
图片预览





文档简介
(共12张PPT)
反比例的意义
(第一课时)
六年级下册第三单元
1.成正比例的量有什么特征?
(1)两种相关联的量;
一种量变化,另一种量也随着变化。
(2)两种量中相对应的两个量的比值(商)
一定。
2.正比例关系式
y
x
=
k
(一定)
复习引入
新课导入
单价(元)
数量(个)
40
…
10
…
12
6
20
5
3
1.5
30
2
1.如果给你60元钱,让你去水果超市买一种水果,你可以买多少个?
2元/个
5元/个
3元/个
6元/个
1.5元/个
10元/个
(1)表中有哪两个量?
(2)单价怎样随着数量的变化而变化?
(3)每两个相对应的数据的乘积是多少?
请同学们仔细观察表中数据,回答老师的三个问题:
单价值扩大,数量值缩小;
单价值缩小,数量值扩大;
单价和数量是两种相关联的量,
单价是随着数量的变化而变化的。
单价×数量=总价(一定)。
3×20=60; 5×12=60; 6×10=60;……
每分钟打字 (个) 120 100 75 60
所需时间 (分) 25 30 60
50
50
40
2.这篇稿子,每分钟打120个字,25分能够打完。
探索规律,并按规律填表。
合作探究
(1)表中有哪两个量?
(2)每分钟打字个数怎样随着所需时间的变化而变化?
(3)每两个相对应的数据的乘积是多少?
请同学们仔细观察表中数据,回答老师的三个问题:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
单价×数量=总价 (积一定)
每分钟打的字数×时间=稿件总字数(积一定)
课堂探索
从上面两个例子中,你发现了什么?
1.两种相关联的量,一种量扩大或缩小,另一种量反而缩小或扩大相同的倍数。
2.两种相关联的量相对应的两个数的乘积是一定的。
课堂探索
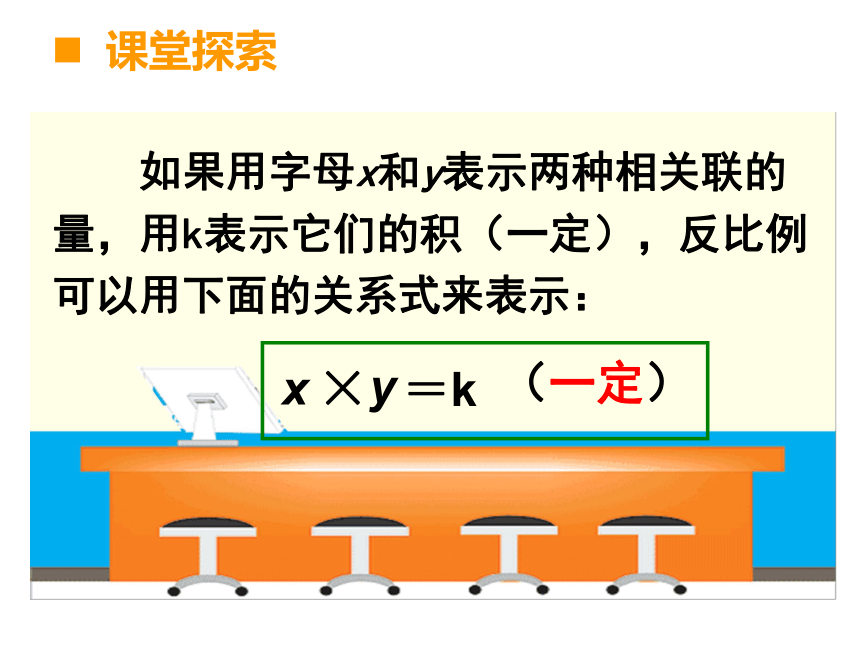
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例可以用下面的关系式来表示:
y
x
=k
(一定)
×
如何判断两个量是否成反比例
1.是否是两种相关联的量;
课堂探索
2.相对应的两个量的乘积是否一定的。
因为:
所以:
1.判断下面每题中的两种量是不是成反比例,并说明理由。
小明从家到学校,骑自行车的速度和所需的时间。
骑自行车的速度和所需的时间是两种相关联的量。
自行车的速度×所需的时间=路程(一定)
骑自行车的速度和所需的时间成反比例。
课堂练习
课堂练习
2.判断下面每题中的两种量是不是成反比例,并说明理由。
长方形的面积一定,它的长和宽。
长×宽=长方形的面积
(一定)
加数 12 12.5 14 24
加数 18 17.5 16 6
12+18=30; 12.5+17.5=30; 14+16=30; 24+6=30
(相关联的两个量和一定,不是乘积一定,不是反比例。)
因数 3 6 8 5
因数 18 9 7 9
3×18=54; 6×9=54; 8×7=56; 5×9=45
(相关联的两个量,乘积不一定,不是反比例。)
巩固提高
课堂总结
→不成比例
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
积一定
商一定
→成反比例
→成正比例
孩子们,学完了这节课你们都有哪些收获呢?
谢谢大家
反比例的意义
(第一课时)
六年级下册第三单元
1.成正比例的量有什么特征?
(1)两种相关联的量;
一种量变化,另一种量也随着变化。
(2)两种量中相对应的两个量的比值(商)
一定。
2.正比例关系式
y
x
=
k
(一定)
复习引入
新课导入
单价(元)
数量(个)
40
…
10
…
12
6
20
5
3
1.5
30
2
1.如果给你60元钱,让你去水果超市买一种水果,你可以买多少个?
2元/个
5元/个
3元/个
6元/个
1.5元/个
10元/个
(1)表中有哪两个量?
(2)单价怎样随着数量的变化而变化?
(3)每两个相对应的数据的乘积是多少?
请同学们仔细观察表中数据,回答老师的三个问题:
单价值扩大,数量值缩小;
单价值缩小,数量值扩大;
单价和数量是两种相关联的量,
单价是随着数量的变化而变化的。
单价×数量=总价(一定)。
3×20=60; 5×12=60; 6×10=60;……
每分钟打字 (个) 120 100 75 60
所需时间 (分) 25 30 60
50
50
40
2.这篇稿子,每分钟打120个字,25分能够打完。
探索规律,并按规律填表。
合作探究
(1)表中有哪两个量?
(2)每分钟打字个数怎样随着所需时间的变化而变化?
(3)每两个相对应的数据的乘积是多少?
请同学们仔细观察表中数据,回答老师的三个问题:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
单价×数量=总价 (积一定)
每分钟打的字数×时间=稿件总字数(积一定)
课堂探索
从上面两个例子中,你发现了什么?
1.两种相关联的量,一种量扩大或缩小,另一种量反而缩小或扩大相同的倍数。
2.两种相关联的量相对应的两个数的乘积是一定的。
课堂探索
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例可以用下面的关系式来表示:
y
x
=k
(一定)
×
如何判断两个量是否成反比例
1.是否是两种相关联的量;
课堂探索
2.相对应的两个量的乘积是否一定的。
因为:
所以:
1.判断下面每题中的两种量是不是成反比例,并说明理由。
小明从家到学校,骑自行车的速度和所需的时间。
骑自行车的速度和所需的时间是两种相关联的量。
自行车的速度×所需的时间=路程(一定)
骑自行车的速度和所需的时间成反比例。
课堂练习
课堂练习
2.判断下面每题中的两种量是不是成反比例,并说明理由。
长方形的面积一定,它的长和宽。
长×宽=长方形的面积
(一定)
加数 12 12.5 14 24
加数 18 17.5 16 6
12+18=30; 12.5+17.5=30; 14+16=30; 24+6=30
(相关联的两个量和一定,不是乘积一定,不是反比例。)
因数 3 6 8 5
因数 18 9 7 9
3×18=54; 6×9=54; 8×7=56; 5×9=45
(相关联的两个量,乘积不一定,不是反比例。)
巩固提高
课堂总结
→不成比例
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
积一定
商一定
→成反比例
→成正比例
孩子们,学完了这节课你们都有哪些收获呢?
谢谢大家
