北师大版七年级数学下册 1.2 幂的乘方 课件(共21张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 1.2 幂的乘方 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 248.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 14:14:02 | ||
图片预览







文档简介
(共21张PPT)
1.2 幂的乘方
数学课上,老师给同学们出了这样一道题目:请比较355,444,533的大小.
因为5>4>3,
所以533>444>355
因为55>44>33,
所以355>444>533
新课导入
你又是如何考虑的呢?
学习目标
1.认识幂的乘方的运算性质;
2.能灵活应用幂的乘方的运算性质进行计算.
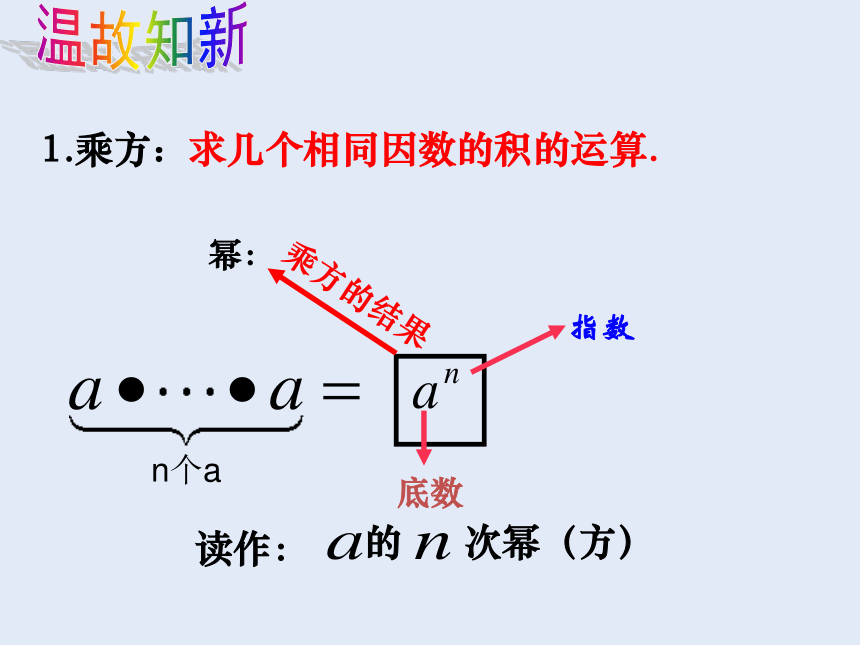
底数
指数
的 次幂(方)
求几个相同因数的积的运算.
1.乘方:
幂:
乘方的结果
n个a
读作:
温故知新
温故知新
2.同底数幂的乘法的运算性质:
同底数幂相乘,底数 ,指数 .
am · an
=am+n
(m,n都是正整数)
不变
相加
如果这个正方体的棱长是 42 cm,那么
它的体积是 cm3.
(42)3=
(42)3
探究新知
4 ×4 ×4
=4 +2+2
=43×
=46
仿照上面的计算过程,计算下列各式,并说明理由 .
(1) (a2)3 ; (2) (am)2 ; (3) (am)n .
仿照上面的计算过程,计算下列各式,并说明理由 .
(1) (a2)3 ; (2) (am)2 ; (3) (am)n ;
(1) (a2)3
(2) (am)2
= a2·a2·a2
=a2+2+2
=a6
=am·am
=am+m
=a2×3
=a2m ;
探究新知
解:
个am
=am·am· … ·am
n
(3) (am)n
=amn
个m
=am+m+ … +m
n
(am)n=amn(其中,m、n为正整数)
归纳总结
幂的乘方,底数 ,指数 .
(am)n=amn (m,n都是正整数)
不变
相乘
幂的乘方运算性质
1.判断下面计算是否正确?正确的说出理由,
不正确的请改正.
(1)(x2)5=x7;
改正:(x2)5 =x2×5=x10
×
(2)a6·a4=a24;
×
改正:a6·a4 =a6+4=a10
(3)x3+ x3=x9;
×
改正:x3+ x3 =2x3
现学现用
(4)(x2)3=x8;
×
改正:(x2)3=x2×3=x6
(5)(y2)3 · y4=y10.
√
2. 填空:
(1)(104)3= ;
(2)(a3)3= ;
(3)-(x3)5= ;
(4)(x2)3 ·(-x)2= .
1012
a9
-x15
x8
例1计算:
(102)4 ; (2) -(a2)m ;
(3) [(xy)4 ]2 ; (4) [(2y-x)2 ]3 .
(1) (102)4
=102×4
=108
(2) -(a2)m
= - a2×m
= - a2m
(3) [(xy)4 ]2
=(xy)4×2
=(xy)8
(4) [(2y-x)2 ]3
= (2y-x)6
解:
温馨提示:幂的乘方运算公式中的底数和指数可以是数字、字母、 单项式、多项式.
请以小组互助学习的形式,完成下列各小题的计算:
交流互助 共同进步
(2) (- x2)3 =
(1)(-x3)2
= x3×2
=x6
(3) -(y2)3
= - y2×3
= - y6
- x2 ×3
=-x6
(4) –(y3)2
= – y6
=-y3×2
解:
指数相乘
指数相加
同底数幂的乘法
幂的乘方
其中m,n都是正整数
底数不变
底数不变
知识梳理
同底数幂的乘法公式逆用:
幂的乘方公式逆用:
amn= (am)n=(an)m
am+n= am·an
其中m,n都是正整数
能力提升
1.已知 am=2,an=3,
求:(1)a2m ,a3n的值;
(3)a2m+3n 的值.
(2)am+n 的值;
解:(1) a2m
=(am)2
=22 =4,
a3n
=(an)3
= 33=27;
(3) a2m+3n
= a2m. a3n
=(am)2. (an)3
=4×27=108.
(2) am+n
= am.an
=2×3=6;
小结
请你谈谈本节课你有哪些收获?
幂的乘方,底数 ,指数 .
(am)n=(an)m =amn (m,n都是正整数)
不变
相乘
幂的乘方运算性质
amn= (am)n=(an)m( m,n都是正整数)
幂的乘方运算公式的逆用:
1.口算:
⑴ (a2)4
⑵(b3m)4
⑶ (xn)m
⑷ (b3)3
⑸ x4·x4
⑹ (x4)7
当堂训练
(8)[(x+y)3]4
⑺ -(y7)2
2.若 am = 2, 则a3m =_____.
3.若 mx = 2, my = 3 ,则 m3x+2y =___.
8
72
4.比较355,444,533的大小.
解:
355=35×11=(35)11=24311
444=44×11=(44)11=25611
533=53×11=(53)11=12511
因为256>243>125
所以444>355>533
家庭作业:习题1.2 1,2
1.2 幂的乘方
数学课上,老师给同学们出了这样一道题目:请比较355,444,533的大小.
因为5>4>3,
所以533>444>355
因为55>44>33,
所以355>444>533
新课导入
你又是如何考虑的呢?
学习目标
1.认识幂的乘方的运算性质;
2.能灵活应用幂的乘方的运算性质进行计算.
底数
指数
的 次幂(方)
求几个相同因数的积的运算.
1.乘方:
幂:
乘方的结果
n个a
读作:
温故知新
温故知新
2.同底数幂的乘法的运算性质:
同底数幂相乘,底数 ,指数 .
am · an
=am+n
(m,n都是正整数)
不变
相加
如果这个正方体的棱长是 42 cm,那么
它的体积是 cm3.
(42)3=
(42)3
探究新知
4 ×4 ×4
=4 +2+2
=43×
=46
仿照上面的计算过程,计算下列各式,并说明理由 .
(1) (a2)3 ; (2) (am)2 ; (3) (am)n .
仿照上面的计算过程,计算下列各式,并说明理由 .
(1) (a2)3 ; (2) (am)2 ; (3) (am)n ;
(1) (a2)3
(2) (am)2
= a2·a2·a2
=a2+2+2
=a6
=am·am
=am+m
=a2×3
=a2m ;
探究新知
解:
个am
=am·am· … ·am
n
(3) (am)n
=amn
个m
=am+m+ … +m
n
(am)n=amn(其中,m、n为正整数)
归纳总结
幂的乘方,底数 ,指数 .
(am)n=amn (m,n都是正整数)
不变
相乘
幂的乘方运算性质
1.判断下面计算是否正确?正确的说出理由,
不正确的请改正.
(1)(x2)5=x7;
改正:(x2)5 =x2×5=x10
×
(2)a6·a4=a24;
×
改正:a6·a4 =a6+4=a10
(3)x3+ x3=x9;
×
改正:x3+ x3 =2x3
现学现用
(4)(x2)3=x8;
×
改正:(x2)3=x2×3=x6
(5)(y2)3 · y4=y10.
√
2. 填空:
(1)(104)3= ;
(2)(a3)3= ;
(3)-(x3)5= ;
(4)(x2)3 ·(-x)2= .
1012
a9
-x15
x8
例1计算:
(102)4 ; (2) -(a2)m ;
(3) [(xy)4 ]2 ; (4) [(2y-x)2 ]3 .
(1) (102)4
=102×4
=108
(2) -(a2)m
= - a2×m
= - a2m
(3) [(xy)4 ]2
=(xy)4×2
=(xy)8
(4) [(2y-x)2 ]3
= (2y-x)6
解:
温馨提示:幂的乘方运算公式中的底数和指数可以是数字、字母、 单项式、多项式.
请以小组互助学习的形式,完成下列各小题的计算:
交流互助 共同进步
(2) (- x2)3 =
(1)(-x3)2
= x3×2
=x6
(3) -(y2)3
= - y2×3
= - y6
- x2 ×3
=-x6
(4) –(y3)2
= – y6
=-y3×2
解:
指数相乘
指数相加
同底数幂的乘法
幂的乘方
其中m,n都是正整数
底数不变
底数不变
知识梳理
同底数幂的乘法公式逆用:
幂的乘方公式逆用:
amn= (am)n=(an)m
am+n= am·an
其中m,n都是正整数
能力提升
1.已知 am=2,an=3,
求:(1)a2m ,a3n的值;
(3)a2m+3n 的值.
(2)am+n 的值;
解:(1) a2m
=(am)2
=22 =4,
a3n
=(an)3
= 33=27;
(3) a2m+3n
= a2m. a3n
=(am)2. (an)3
=4×27=108.
(2) am+n
= am.an
=2×3=6;
小结
请你谈谈本节课你有哪些收获?
幂的乘方,底数 ,指数 .
(am)n=(an)m =amn (m,n都是正整数)
不变
相乘
幂的乘方运算性质
amn= (am)n=(an)m( m,n都是正整数)
幂的乘方运算公式的逆用:
1.口算:
⑴ (a2)4
⑵(b3m)4
⑶ (xn)m
⑷ (b3)3
⑸ x4·x4
⑹ (x4)7
当堂训练
(8)[(x+y)3]4
⑺ -(y7)2
2.若 am = 2, 则a3m =_____.
3.若 mx = 2, my = 3 ,则 m3x+2y =___.
8
72
4.比较355,444,533的大小.
解:
355=35×11=(35)11=24311
444=44×11=(44)11=25611
533=53×11=(53)11=12511
因为256>243>125
所以444>355>533
家庭作业:习题1.2 1,2
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
