北师大版七年级数学下册 4.2 图形的全等 课件(共37张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 4.2 图形的全等 课件(共37张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 486.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 00:00:00 | ||
图片预览





文档简介
(共37张PPT)
3.2 图形的全等
第三章 三角形
教学目标:1、借助具体的情景和图形,了解全等三角形的概念,明确全等三角形的性质,并能应用性质进行简单的合情推理和计算。
2、能根据对应角或对应边的线索、按全等变换,找出其它的对应顶点、对应边、对应角。
3、借助符号语言表示三角形全等,丰富学生的符号感;通过对全等变换过程的体验,提高学生的识图能力。
4、通过做数学的过程,培养学生热爱并乐于研究数学的积极情感。
通过观察我们发现,这些图形中有些是完全一样的,如果把它们叠在一起,它们就能重合.
能够完全重合的两个图形称为全等图形.
大小
不同
观察下面两组图形,它们是不是全等图形?为什么?
形状
不同
如果两个图形全等,它们的形状和大小一定都相同.
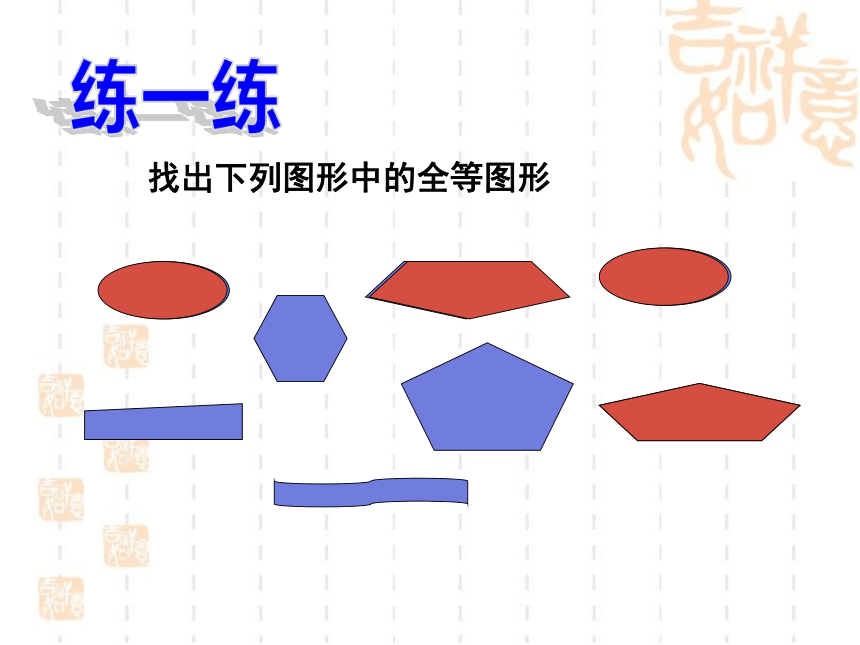
找出下列图形中的全等图形
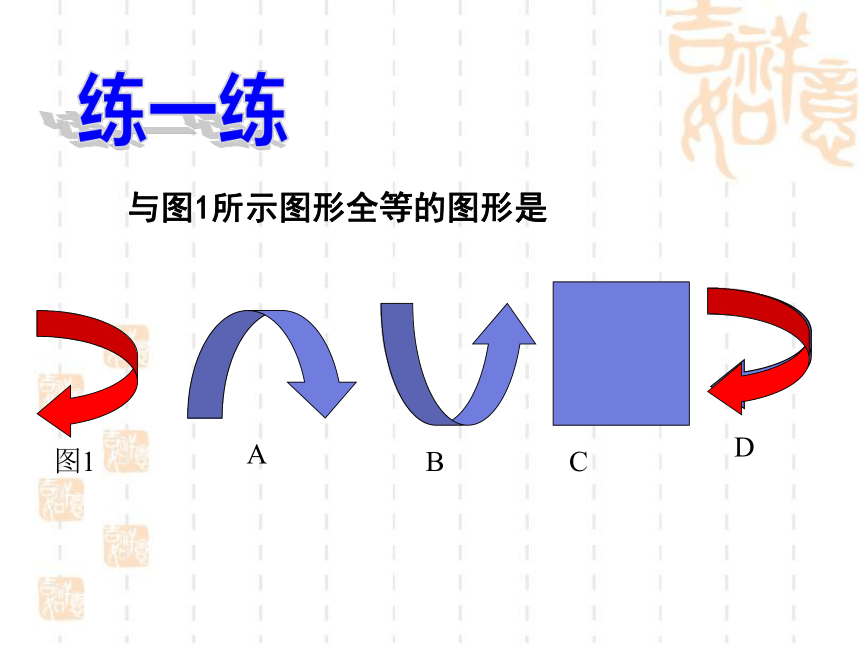
与图1所示图形全等的图形是
图1
A
B
C
D
将图2绕A点顺时针转90°所得到的图形是
图2
D
A
B
C
A
B
C
我们把能完全重合的三角形叫做全等三角形.
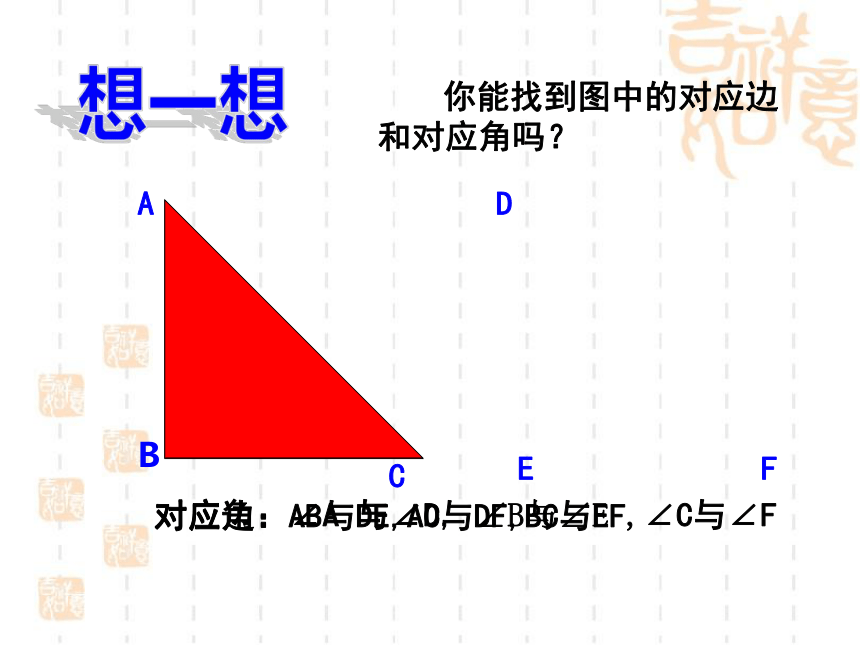
你能找到图中的对应边和对应角吗?
A
B
C
D
E
F
对应边:AB与DE,AC与DF,BC与EF
对应角:∠A 与∠D, ∠B与∠E ,∠C与∠F
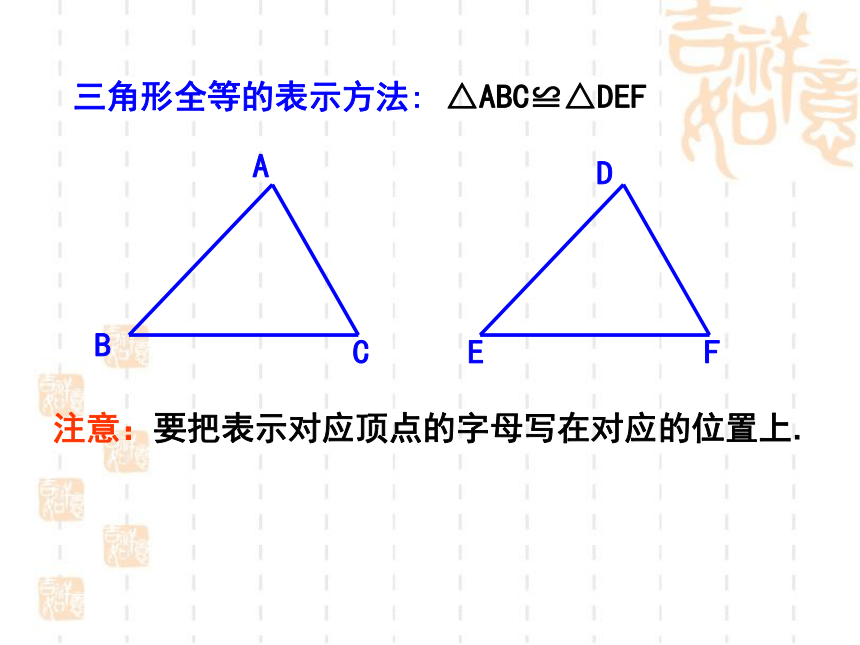
三角形全等的表示方法:
△ABC≌△DEF
A
B
C
D
E
F
注意:要把表示对应顶点的字母写在对应的位置上.
全等三角形的对应边相等,对应角相等
你能将一个等边三角形分
成两个全等三角形吗?
能把它分成三个,四个
全等三角形吗?
你能将一个等边三角形分
成两个全等三角形吗?
能把它分成三个,四个
全等三角形吗?
你能将一个等边三角形分
成两个全等三角形吗?
能把它分成三个,四个
全等三角形吗?
已知:△ABC≌△ADC
与BC对应的线段:_______
与AD对应的线段:_______
与AC对应的线段:________与∠ACB对应的角:________与∠B对应的角:_________与
∠BAC对应的角:____________
D
C
B
A
DC
AB
AC
∠ACD
∠D
∠DAC
已知:△ACE≌△DFB 则:
对应角有:________________________________
对应边有:_____________________
A
C
B
D
E
F
AC与DF,AE与DB,CE与FB
∠A 与∠D, ∠C与∠F, ∠AEC与∠DBF
如图:△AOD≌△BOC,写出其中相等的角
A
D
C
B
O
解:∠A=∠B
∠D=∠C
∠DOA=∠COB
如图,已知⊿ABD≌⊿ACE,∠B=∠C,∠ADB=∠AEC,请用等式表示其它的对应边和对应角.
A
B
C
D
E
AB=AC
AD=AE
BD=CE
∠BAD=∠CAE
若 ⊿ABE≌⊿ACD,∠B=∠C,∠ADC=∠AEB,请用等式表示其它的对应边和对应角.
A
B
C
D
E
AB=AC
AE=AD
BE=CD
∠BAE=∠CAD
如图:△ABC≌△AEC, ∠B=30°, ∠ACB=85°,求出△AEC各内角的度数.
A
B
C
E
解:因为△AEC≌△ABC
所以∠E=∠B=30°
∠ACE=∠ACB=85°
∠EAC=∠BAC=180°-30°-85°=65°
如图,△ABC≌△DEF,∠C=25°,BC=6cm,AC=4cm ,
你能得出△DEF中哪些角的大小,哪些边的长度
A
B
C
D
E
F
因为△DEF≌△ABC
所以∠F=∠C=25°
EF=BC=6cm
DF=AC=4cm
解:
如图,△ABC≌△DEF,求证:AD=BE
B
A
E
F
C
D
因为△ABC≌△DEF
所以AB=DE
AB-BD=DE-BD
即AD=BE
证明:
如图,若△ABC≌△EFC,
点B、C、E在同一条直线
上,且CF=3cm, CE=7cm,
∠EFC=64°,则BC=_____cm, AC=_____cm, ∠B=_____.
B
A
E
F
C
3
64°
你还能求出哪些边的长度,哪些角的度数
7
AF=4cm
∠ACB=∠ECF= 90°
∠A= ∠E=26°
已知:⊿MNP≌⊿ABC,MN=AB,MP=AC,∠MPN=35 ,∠CAB=40 ,则∠ABC=____,∠M=____.
分析:本题没有图,可以从两个角度出 发,一个是根据题意作图,另一个就是找到对应顶点.
已知:⊿MNP≌⊿ABC,MN=AB,MP=AC,∠MPN=35 ,∠CAB=40 ,则∠ABC=____,∠M=____.
思路:由已知MN=AB,MP=AC,可以得到对应顶点分别是M与A,N与B,P与C.
由此可得: ∠M=∠CAB=40 ,∠ACB=∠MPN=35
所以∠ABC=180 -∠CAB-∠ACB=105
105
40
如图:⊿ADC≌⊿BFE,
∠E=∠C,AB=7,
DF=3,求AF的长?
A
B
C
E
F
D
A
B
C
E
F
D
解:
∵⊿ADC≌⊿BFE,∠E=∠C
∴AD=BF
∴AD-DF=BF-DF
即AF=BD
又∵ AF+BD=AB-DF=7-3=4(cm)
∴AF=BD=2cm
如图, ⊿ABE≌⊿DCF ,∠A=∠D,BF=7cm,CF=3cm,求EF的长.
A
B
E
F
D
C
解:
∵⊿ABE≌⊿DCF ,∠A=∠D
∴BE=CF=3cm
∴EF=BF-BE=4cm
如图△ABF≌△DCE ,在三角形对应边和对应角以外,你还能得到什么结论?
A
F
E
D
C
B
AE=DF
分析:
∵⊿ABF≌⊿DCE
∴AF=DE
∴AF-EF=DE-EF
即AE=DF
如图△ABF≌△DCE ,在三角形对应边和对应角以外,你还能得到什么结论?
A
F
E
D
C
B
分析:
∵⊿ABF≌⊿DCE
∴ ∠AFB=∠DEC
∴ ∠AEC=∠DFB
(等角的补角相等)
∠AEC=∠DFB
如图△ABF≌△DCE ,在三角形对应边和对应角以外,你还能得到什么结论?
A
F
E
D
C
B
分析:
∵⊿ABF≌⊿DCE
∴∠A=∠D,∠AFB=∠DEC
∴ AB∥CD, BF∥CE
(内错角相等,两直线平行)
AB∥CD
BF∥CE
一.你能把下面的这个平行四边形
2.分成四个全等的图形吗?
1.图形的全等概念
2.三角形全等的性质
能够完全重合的两个图形称为全等图形.
我们把能完全重合的三角形叫做全等三角形.
全等三角形的对应边相等,对应角相等.
如图,△ABC≌△EBD,问∠1与∠2相等吗 若相等请证明,若不相等说出为什么
B
A
E
2
1
F
C
D
O
分析: ∠1与∠2分别在
△AOF与△EOB中,显而
易见∠AOF与∠EOB是
对顶角,而∠A与∠E是△ABC与△EBD的对应
角,可由三角形内角和得到∠1与∠2相等.
如图,△ABC≌△EBD,问∠1与∠2相等吗 若相等请证明,若不相等说出为什么
B
A
E
2
1
F
C
D
O
解:因为△EBD≌△ABC
所以∠A=∠E
在△AOF与△EOB中,
∠AOF=∠EOB
根据三角形内角和为180°
所以 ∠1=∠2
3.2 图形的全等
第三章 三角形
教学目标:1、借助具体的情景和图形,了解全等三角形的概念,明确全等三角形的性质,并能应用性质进行简单的合情推理和计算。
2、能根据对应角或对应边的线索、按全等变换,找出其它的对应顶点、对应边、对应角。
3、借助符号语言表示三角形全等,丰富学生的符号感;通过对全等变换过程的体验,提高学生的识图能力。
4、通过做数学的过程,培养学生热爱并乐于研究数学的积极情感。
通过观察我们发现,这些图形中有些是完全一样的,如果把它们叠在一起,它们就能重合.
能够完全重合的两个图形称为全等图形.
大小
不同
观察下面两组图形,它们是不是全等图形?为什么?
形状
不同
如果两个图形全等,它们的形状和大小一定都相同.
找出下列图形中的全等图形
与图1所示图形全等的图形是
图1
A
B
C
D
将图2绕A点顺时针转90°所得到的图形是
图2
D
A
B
C
A
B
C
我们把能完全重合的三角形叫做全等三角形.
你能找到图中的对应边和对应角吗?
A
B
C
D
E
F
对应边:AB与DE,AC与DF,BC与EF
对应角:∠A 与∠D, ∠B与∠E ,∠C与∠F
三角形全等的表示方法:
△ABC≌△DEF
A
B
C
D
E
F
注意:要把表示对应顶点的字母写在对应的位置上.
全等三角形的对应边相等,对应角相等
你能将一个等边三角形分
成两个全等三角形吗?
能把它分成三个,四个
全等三角形吗?
你能将一个等边三角形分
成两个全等三角形吗?
能把它分成三个,四个
全等三角形吗?
你能将一个等边三角形分
成两个全等三角形吗?
能把它分成三个,四个
全等三角形吗?
已知:△ABC≌△ADC
与BC对应的线段:_______
与AD对应的线段:_______
与AC对应的线段:________与∠ACB对应的角:________与∠B对应的角:_________与
∠BAC对应的角:____________
D
C
B
A
DC
AB
AC
∠ACD
∠D
∠DAC
已知:△ACE≌△DFB 则:
对应角有:________________________________
对应边有:_____________________
A
C
B
D
E
F
AC与DF,AE与DB,CE与FB
∠A 与∠D, ∠C与∠F, ∠AEC与∠DBF
如图:△AOD≌△BOC,写出其中相等的角
A
D
C
B
O
解:∠A=∠B
∠D=∠C
∠DOA=∠COB
如图,已知⊿ABD≌⊿ACE,∠B=∠C,∠ADB=∠AEC,请用等式表示其它的对应边和对应角.
A
B
C
D
E
AB=AC
AD=AE
BD=CE
∠BAD=∠CAE
若 ⊿ABE≌⊿ACD,∠B=∠C,∠ADC=∠AEB,请用等式表示其它的对应边和对应角.
A
B
C
D
E
AB=AC
AE=AD
BE=CD
∠BAE=∠CAD
如图:△ABC≌△AEC, ∠B=30°, ∠ACB=85°,求出△AEC各内角的度数.
A
B
C
E
解:因为△AEC≌△ABC
所以∠E=∠B=30°
∠ACE=∠ACB=85°
∠EAC=∠BAC=180°-30°-85°=65°
如图,△ABC≌△DEF,∠C=25°,BC=6cm,AC=4cm ,
你能得出△DEF中哪些角的大小,哪些边的长度
A
B
C
D
E
F
因为△DEF≌△ABC
所以∠F=∠C=25°
EF=BC=6cm
DF=AC=4cm
解:
如图,△ABC≌△DEF,求证:AD=BE
B
A
E
F
C
D
因为△ABC≌△DEF
所以AB=DE
AB-BD=DE-BD
即AD=BE
证明:
如图,若△ABC≌△EFC,
点B、C、E在同一条直线
上,且CF=3cm, CE=7cm,
∠EFC=64°,则BC=_____cm, AC=_____cm, ∠B=_____.
B
A
E
F
C
3
64°
你还能求出哪些边的长度,哪些角的度数
7
AF=4cm
∠ACB=∠ECF= 90°
∠A= ∠E=26°
已知:⊿MNP≌⊿ABC,MN=AB,MP=AC,∠MPN=35 ,∠CAB=40 ,则∠ABC=____,∠M=____.
分析:本题没有图,可以从两个角度出 发,一个是根据题意作图,另一个就是找到对应顶点.
已知:⊿MNP≌⊿ABC,MN=AB,MP=AC,∠MPN=35 ,∠CAB=40 ,则∠ABC=____,∠M=____.
思路:由已知MN=AB,MP=AC,可以得到对应顶点分别是M与A,N与B,P与C.
由此可得: ∠M=∠CAB=40 ,∠ACB=∠MPN=35
所以∠ABC=180 -∠CAB-∠ACB=105
105
40
如图:⊿ADC≌⊿BFE,
∠E=∠C,AB=7,
DF=3,求AF的长?
A
B
C
E
F
D
A
B
C
E
F
D
解:
∵⊿ADC≌⊿BFE,∠E=∠C
∴AD=BF
∴AD-DF=BF-DF
即AF=BD
又∵ AF+BD=AB-DF=7-3=4(cm)
∴AF=BD=2cm
如图, ⊿ABE≌⊿DCF ,∠A=∠D,BF=7cm,CF=3cm,求EF的长.
A
B
E
F
D
C
解:
∵⊿ABE≌⊿DCF ,∠A=∠D
∴BE=CF=3cm
∴EF=BF-BE=4cm
如图△ABF≌△DCE ,在三角形对应边和对应角以外,你还能得到什么结论?
A
F
E
D
C
B
AE=DF
分析:
∵⊿ABF≌⊿DCE
∴AF=DE
∴AF-EF=DE-EF
即AE=DF
如图△ABF≌△DCE ,在三角形对应边和对应角以外,你还能得到什么结论?
A
F
E
D
C
B
分析:
∵⊿ABF≌⊿DCE
∴ ∠AFB=∠DEC
∴ ∠AEC=∠DFB
(等角的补角相等)
∠AEC=∠DFB
如图△ABF≌△DCE ,在三角形对应边和对应角以外,你还能得到什么结论?
A
F
E
D
C
B
分析:
∵⊿ABF≌⊿DCE
∴∠A=∠D,∠AFB=∠DEC
∴ AB∥CD, BF∥CE
(内错角相等,两直线平行)
AB∥CD
BF∥CE
一.你能把下面的这个平行四边形
2.分成四个全等的图形吗?
1.图形的全等概念
2.三角形全等的性质
能够完全重合的两个图形称为全等图形.
我们把能完全重合的三角形叫做全等三角形.
全等三角形的对应边相等,对应角相等.
如图,△ABC≌△EBD,问∠1与∠2相等吗 若相等请证明,若不相等说出为什么
B
A
E
2
1
F
C
D
O
分析: ∠1与∠2分别在
△AOF与△EOB中,显而
易见∠AOF与∠EOB是
对顶角,而∠A与∠E是△ABC与△EBD的对应
角,可由三角形内角和得到∠1与∠2相等.
如图,△ABC≌△EBD,问∠1与∠2相等吗 若相等请证明,若不相等说出为什么
B
A
E
2
1
F
C
D
O
解:因为△EBD≌△ABC
所以∠A=∠E
在△AOF与△EOB中,
∠AOF=∠EOB
根据三角形内角和为180°
所以 ∠1=∠2
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
