5.3.1 函数的单调性(第一课时) 课件(27张ppt)-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 5.3.1 函数的单调性(第一课时) 课件(27张ppt)-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 21:21:28 | ||
图片预览




文档简介
5.3.1 函数的单调性(第一课时)
?
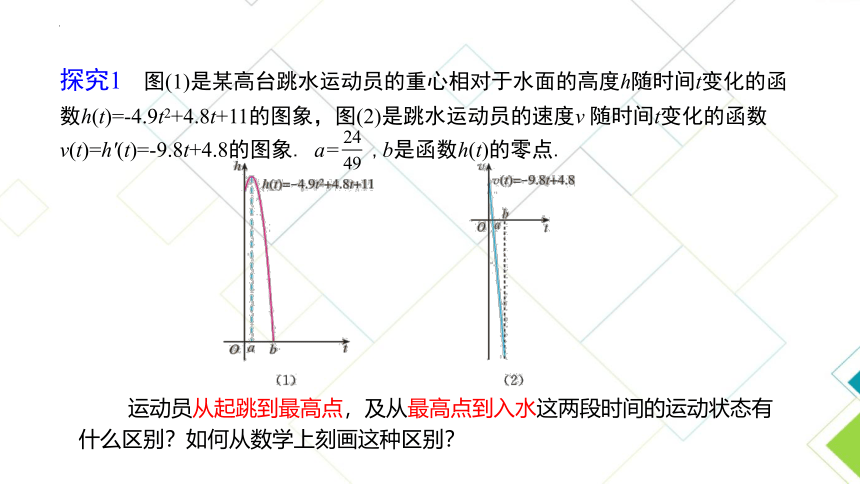
运动员从起跳到最高点,及从最高点到入水这两段时间的运动状态有什么区别?如何从数学上刻画这种区别?
探究1 图(1)是某高台跳水运动员的重心相对于水面的高度h随时间t变化的函数h(t)=-4.9t2+4.8t+11的图象,图(2)是跳水运动员的速度v 随时间t变化的函数v(t)=h′(t)=-9.8t+4.8的图象. a= ,b是函数h(t)的零点.
观察图象可以发现:
(1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度h随时间t的增加而增加,即h(t)单调递增.相应地,v(t)=h′(t)>0.
(2)从最高点到入水,运动员的重心处于下降状态,离水面的高度h随时间t的增加而减小,即h(t)单调递减.相应地,v(t)=h′(t)<0.
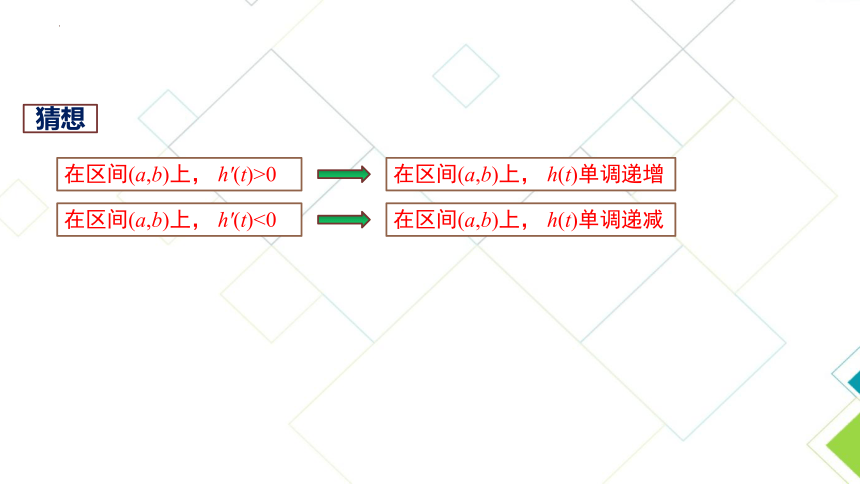
在区间(a,b)上, h′(t)>0
在区间(a,b)上, h′(t)<0
在区间(a,b)上, h(t)单调递增
在区间(a,b)上, h(t)单调递减
猜想
x
y
O
y=x
(1)
x
y
O
y=x2
(2)
x
y
O
y=x3
(3)
x
y
O
(4)
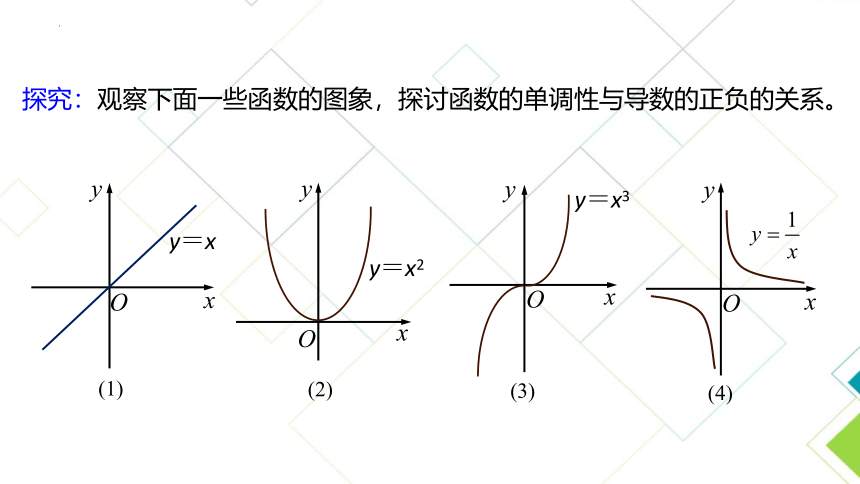
探究:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系。
x
y
O
f (x)=x
(1)
x
y
O
f ′(x)=1
在(-∞, +∞)上, f (x)单调递增
在(-∞, +∞)上,f ′ (x)>0
在(-∞, 0)上, f (x)单调递减
在(-∞, 0)上, f ′ (x)<0
x
y
O
f (x) =x2
(2)
x
y
O
f ′(x)=2x
在(0, +∞)上, f (x)单调递增
在(0, +∞)上,f ′ (x)>0
在(-∞, 0)上, f (x)单调递增
在(-∞, 0)上, f ′ (x)>0
x
y
O
f ′ (x) =3x2
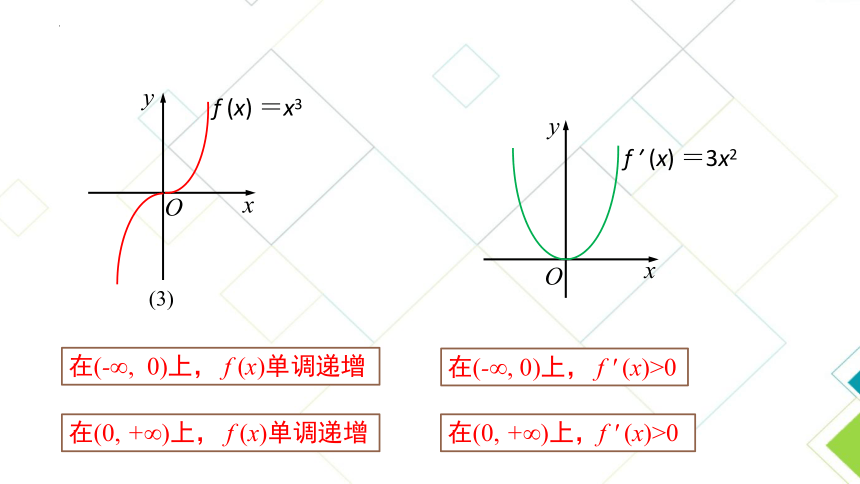
在(0, +∞)上, f (x)单调递增
在(0, +∞)上,f ′ (x)>0
x
y
O
f (x) =x3
(3)
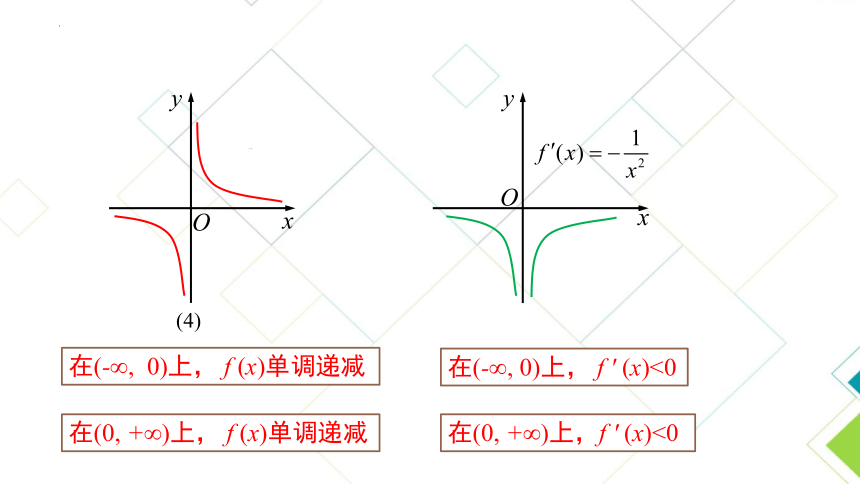
在(-∞, 0)上, f (x)单调递减
在(-∞, 0)上, f ′ (x)<0
在(0, +∞)上, f (x)单调递减
在(0, +∞)上,f ′ (x)<0
x
y
O
(4)
x
y
O
问题:能否由f′(x)的正负来判断函数f(x)的单调性呢?
f ?(x1)<0
f (x)在x1附近下降
切线“左上右下”
在区间上, f ′(x)<0
在区间上,f (x) 单调递减
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
1、定义:一般地,设函数y=f(x)在某个区间(a,b)内有导数,
在某个区间(a,b)上,如果f '(x)> 0,那么函数y=f(x) 在区间(a,b)上单调递增;
在某个区间(a,b)上,如果f '(x)< 0,那么函数y=f(x) 在区间(a,b)上单调递减;
反之如何?
例1 利用导数判断下列函数的单调性:
(1)f(x)=x3+3x; (2) f(x)=sinx-x,x∈(0,π) (3) f(x)=?????1????.
?
例1 利用导数判断下列函数的单调性:
(1)f(x)=x3+3x; (2) f(x)=sinx-x,x∈(0,π) (3) f(x)=?????1????.
?
解:(1)因为f(x)=x3+3x,
所以f '(x)=3x2+3=3(x2+1)>0.
所以,函数f(x)=x3+3x在R上单调递增,如图所示.
(2)因为f(x)=sinx-x,x∈(0,π),
所以f '(x)=cosx-1<0.
所以,函数f(x)=sinx-x在(0,π)上单调递减,如图所示.
练习1.判断下列函数的单调性:
(1)f(x)=x2-2x+4; (2)f(x)=ex-x.
解: (1)函数f(x)=x2-2x+4在(-∞,1)上单调递减,在(1,+∞)上单调递增.
(2)函数f(x)=ex-x在(-∞,0)上单调递减,在(0,+∞)上单调递增.
C
小结反思
C
B
?
运动员从起跳到最高点,及从最高点到入水这两段时间的运动状态有什么区别?如何从数学上刻画这种区别?
探究1 图(1)是某高台跳水运动员的重心相对于水面的高度h随时间t变化的函数h(t)=-4.9t2+4.8t+11的图象,图(2)是跳水运动员的速度v 随时间t变化的函数v(t)=h′(t)=-9.8t+4.8的图象. a= ,b是函数h(t)的零点.
观察图象可以发现:
(1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度h随时间t的增加而增加,即h(t)单调递增.相应地,v(t)=h′(t)>0.
(2)从最高点到入水,运动员的重心处于下降状态,离水面的高度h随时间t的增加而减小,即h(t)单调递减.相应地,v(t)=h′(t)<0.
在区间(a,b)上, h′(t)>0
在区间(a,b)上, h′(t)<0
在区间(a,b)上, h(t)单调递增
在区间(a,b)上, h(t)单调递减
猜想
x
y
O
y=x
(1)
x
y
O
y=x2
(2)
x
y
O
y=x3
(3)
x
y
O
(4)
探究:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系。
x
y
O
f (x)=x
(1)
x
y
O
f ′(x)=1
在(-∞, +∞)上, f (x)单调递增
在(-∞, +∞)上,f ′ (x)>0
在(-∞, 0)上, f (x)单调递减
在(-∞, 0)上, f ′ (x)<0
x
y
O
f (x) =x2
(2)
x
y
O
f ′(x)=2x
在(0, +∞)上, f (x)单调递增
在(0, +∞)上,f ′ (x)>0
在(-∞, 0)上, f (x)单调递增
在(-∞, 0)上, f ′ (x)>0
x
y
O
f ′ (x) =3x2
在(0, +∞)上, f (x)单调递增
在(0, +∞)上,f ′ (x)>0
x
y
O
f (x) =x3
(3)
在(-∞, 0)上, f (x)单调递减
在(-∞, 0)上, f ′ (x)<0
在(0, +∞)上, f (x)单调递减
在(0, +∞)上,f ′ (x)<0
x
y
O
(4)
x
y
O
问题:能否由f′(x)的正负来判断函数f(x)的单调性呢?
f ?(x1)<0
f (x)在x1附近下降
切线“左上右下”
在区间上, f ′(x)<0
在区间上,f (x) 单调递减
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
1、定义:一般地,设函数y=f(x)在某个区间(a,b)内有导数,
在某个区间(a,b)上,如果f '(x)> 0,那么函数y=f(x) 在区间(a,b)上单调递增;
在某个区间(a,b)上,如果f '(x)< 0,那么函数y=f(x) 在区间(a,b)上单调递减;
反之如何?
例1 利用导数判断下列函数的单调性:
(1)f(x)=x3+3x; (2) f(x)=sinx-x,x∈(0,π) (3) f(x)=?????1????.
?
例1 利用导数判断下列函数的单调性:
(1)f(x)=x3+3x; (2) f(x)=sinx-x,x∈(0,π) (3) f(x)=?????1????.
?
解:(1)因为f(x)=x3+3x,
所以f '(x)=3x2+3=3(x2+1)>0.
所以,函数f(x)=x3+3x在R上单调递增,如图所示.
(2)因为f(x)=sinx-x,x∈(0,π),
所以f '(x)=cosx-1<0.
所以,函数f(x)=sinx-x在(0,π)上单调递减,如图所示.
练习1.判断下列函数的单调性:
(1)f(x)=x2-2x+4; (2)f(x)=ex-x.
解: (1)函数f(x)=x2-2x+4在(-∞,1)上单调递减,在(1,+∞)上单调递增.
(2)函数f(x)=ex-x在(-∞,0)上单调递减,在(0,+∞)上单调递增.
C
小结反思
C
B
