5.3.1 函数的单调性(第二课时)课件(17张ppt)-2021-2022学年高二下学期数学 人教A版(2019)选择性必修第二册
文档属性
| 名称 | 5.3.1 函数的单调性(第二课时)课件(17张ppt)-2021-2022学年高二下学期数学 人教A版(2019)选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 21:23:33 | ||
图片预览






文档简介
5.3.1 函数的单调性(第二课时)
?
一般地,函数f (x)的单调性与导函数f ′(x)的正负之间具有如下的关系:
在某个区间(a,b)上,如果f ′(x)>0 ,那么函数y=f (x)在区间(a,b)上单调递增;
在某个区间(a,b)上,如果f ′(x)<0 ,那么函数y=f (x)在区间(a,b)上单调递减.
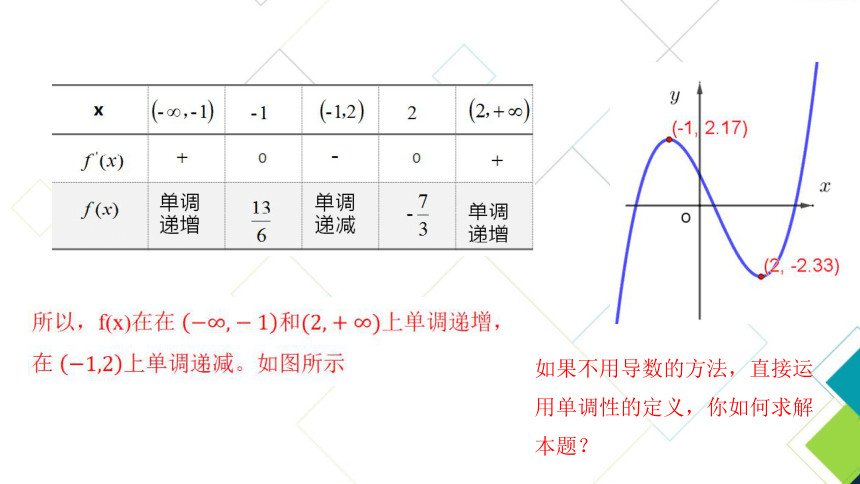
探究1. 形如f(x)=ax3+bx2+cx+d(a≠0)的函数应用广泛,下面我们利用导数来研究这类函数的单调性。
如果不用导数的方法,直接运用单调性的定义,你如何求解本题?
利用导数研究函数y=f (x)的单调性的优势:
不熟悉的、复杂的函数
熟悉的、简单的函数
转化
探究2:研究对数函数y=lnx与幂函数y=x3在区间(0,+∞)上增长快慢的情况.
函数增减的快慢与导数的关系:
一般地,设函数y=f(x),在区间(a, b)上:
如果导数的绝对值越小,函数在区间(a, b)上变化得较慢,函数的图象就比较“平缓”;
反之,如果导数的绝对值越大,函数在区间(a, b)上变化得较快,函数的图象就比较“陡峭”.
例2:设x>0,f(x)=lnx,g(x)=1-1????,两个函数的图象如图所示.判断f(x),g(x)的图象与C1,C2之间的对应关系.
?
所以,f(x),g(x)的图象依次是图中的C2,C1。
课堂小结
利用导数讨论函数单调的步骤:
(1):求函数定义域
(3)令 =0解方程,得方程的根。
(4)列表:方程 =0的根将函数的定义域分成若干个区间,利用表格判断各区间的正负。
(5) 大于0的区间是 f(x)的单调递增区间;
小于0的区间是 f(x)的单调递减区间.
(2):求导数
练习2.判断下列函数的单调性,并求出单调区间:
(1)f(x)=3x-x3; (2) f(x)=x3-x2-x.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单调递减
单调递增
单调递减
所以, 在 和 上单调递减,在 上单调递增,如图所示.
解:(1)函数 的定义域为 .
对 求导数,得
令 ,解得 ,或
解:(2)函数 的定义域为 .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单调递增
单调递减
单调递增
所以, 在 和 上单调递增,在 上单调递减,如图所示.
对 求导数,得
令 ,解得 ,或 .
3.证明函数f(x)=2x3-6x2+7在区间(0,2)上单调递减.
证明:函数 的定义域为 .
当 时, ,
因此函数 区间 上单调递减.
对 求导数,得
?
一般地,函数f (x)的单调性与导函数f ′(x)的正负之间具有如下的关系:
在某个区间(a,b)上,如果f ′(x)>0 ,那么函数y=f (x)在区间(a,b)上单调递增;
在某个区间(a,b)上,如果f ′(x)<0 ,那么函数y=f (x)在区间(a,b)上单调递减.
探究1. 形如f(x)=ax3+bx2+cx+d(a≠0)的函数应用广泛,下面我们利用导数来研究这类函数的单调性。
如果不用导数的方法,直接运用单调性的定义,你如何求解本题?
利用导数研究函数y=f (x)的单调性的优势:
不熟悉的、复杂的函数
熟悉的、简单的函数
转化
探究2:研究对数函数y=lnx与幂函数y=x3在区间(0,+∞)上增长快慢的情况.
函数增减的快慢与导数的关系:
一般地,设函数y=f(x),在区间(a, b)上:
如果导数的绝对值越小,函数在区间(a, b)上变化得较慢,函数的图象就比较“平缓”;
反之,如果导数的绝对值越大,函数在区间(a, b)上变化得较快,函数的图象就比较“陡峭”.
例2:设x>0,f(x)=lnx,g(x)=1-1????,两个函数的图象如图所示.判断f(x),g(x)的图象与C1,C2之间的对应关系.
?
所以,f(x),g(x)的图象依次是图中的C2,C1。
课堂小结
利用导数讨论函数单调的步骤:
(1):求函数定义域
(3)令 =0解方程,得方程的根。
(4)列表:方程 =0的根将函数的定义域分成若干个区间,利用表格判断各区间的正负。
(5) 大于0的区间是 f(x)的单调递增区间;
小于0的区间是 f(x)的单调递减区间.
(2):求导数
练习2.判断下列函数的单调性,并求出单调区间:
(1)f(x)=3x-x3; (2) f(x)=x3-x2-x.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单调递减
单调递增
单调递减
所以, 在 和 上单调递减,在 上单调递增,如图所示.
解:(1)函数 的定义域为 .
对 求导数,得
令 ,解得 ,或
解:(2)函数 的定义域为 .
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单调递增
单调递减
单调递增
所以, 在 和 上单调递增,在 上单调递减,如图所示.
对 求导数,得
令 ,解得 ,或 .
3.证明函数f(x)=2x3-6x2+7在区间(0,2)上单调递减.
证明:函数 的定义域为 .
当 时, ,
因此函数 区间 上单调递减.
对 求导数,得
