5.3.2.2 函数的最大(小)值 课件-2021-2022学年高二下学期数学 人教A版(2019)选择性必修第二册(21张ppt)
文档属性
| 名称 | 5.3.2.2 函数的最大(小)值 课件-2021-2022学年高二下学期数学 人教A版(2019)选择性必修第二册(21张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 21:24:43 | ||
图片预览







文档简介
(共21张PPT)
函数的最大(小)值
f (x)<0
y
x
O
x1
a
b
y=f(x)
极大值点两侧
极小值点两侧
f (x)<0
f (x)>0
f (x)>0
x2
结论:极值点处,f (x) =0
导数与极值的关系
求解函数极值的一般步骤:
(1)确定函数的定义域
(2)求函数的导数f ,(x)
(3)求方程f ,(x)=0的根
(4)用方程f ,(x)=0的根,顺次将函数的定义域分成 若干个开区间,并列成表格
(5)由f ,(x)在方程f ,(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
(2) 由负变正,那么 是极小值点;
(3) 不变号,那么 不是极值点。
(1) 由正变负,那么 是极大值点;
由导函数图像判断极值
在社会生活实践中,为了发挥最大的经济效益,常常遇到如何能使用料最省、产量最高,效益最大等问题,这些问题的解决常常可转化为求一个函数的最大值和最小值问题
函数在什么条件下一定有最大、最小值?他们与函数极值关系如何?
极值是一个局部概念,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小。
问题导学:
3.求函数最值的一般方法
一是利用函数性质 二是利用不等式
三是利用导数
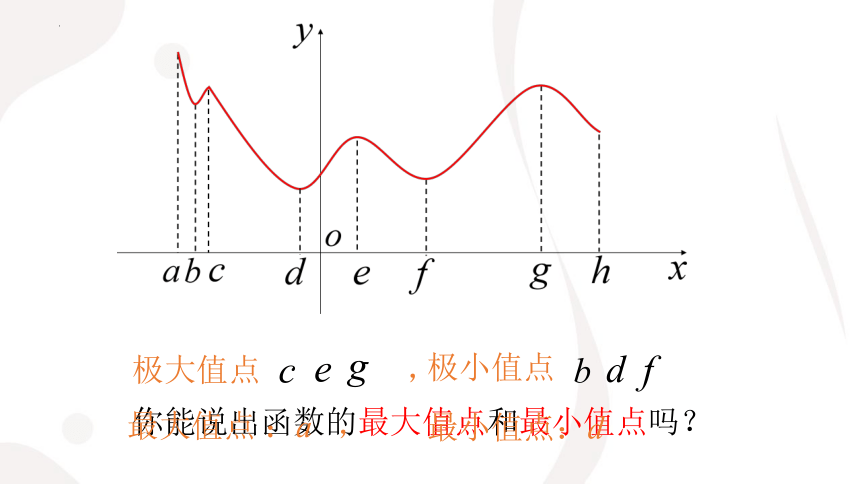
观察区间[a,b]上函数y=f (x)的图象,
你能找出它的极大值点,极小值点吗?
极大值点 ,
极小值点
你能说出函数的最大值点和最小值点吗?
最大值点 :a ,
最小值点:d
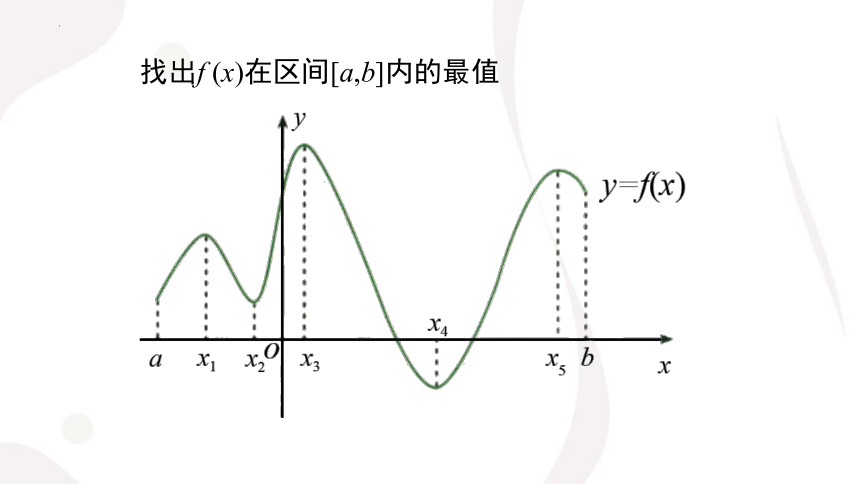
找出f (x)在区间[a,b]内的最值
找出f (x)在区间[a,b]内的最值
函数最值的概念
定义:可导函数 在闭区间[a,b]上所有点处的函数值中最大(或最小)值,叫做函数 的最大(或最小)值。
一般地,在闭区间上连续的函数
在[a,b]上必有最大值与最小值。
x
o
y
a
x1
b
y=f(x)
x2
x3
x4
x5
x6
x
o
y
a
x1
b
y=f(x)
x2
x3
x4
x5
x6
在开区间(a,b)内的连续函数不一定有最大值与最小值.
在闭区间[a,b]上的连续函数必有最大值与最小值
因此:该函数没有最大值.
f(x)max=f(a), f(x)min=f(x3)
·
·
思考:如何求出函数在[a,b]上的最值?
一般的如果在区间[a,b]上,函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
只要把函数y=f (x)的所有极值连同端点的函数值进行比较即可得到最大最小值。
一般地,利用导数求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下:
(2)将y=f(x)的各极值与端点处函数值f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(1)求f(x)在区间(a,b)内的极值(极大值或极小值)
例6: 求在[0,3]的最大值与最小值.
解:
由例5可知当x=2时有极小值,
1.求出所有导数为0的点;
2.计算端点值;
3.比较确定最值
例6: 求在[0,3]的最大值与最小值.
求函数y=f (x)在[a,b]上的最大值与最小值的步骤:
①求函数y=f (x)在(a,b)内的极值;
②将函数y=f (x)的各极值与端点处的函数值f (a), f (b)比较,其中最大的一个是最大值,最小的一个是最小值.
注意
1) 函数的最值概念是全局性的
2) 函数的最大值(最小值)唯一
3) 函数的最大值大于等于最小值
4) 函数的最值可在端点处取得
1.求下列函数的极值∶
(1)f(x)=6x -x-2,x∈[0,2]; (2)f(x)=x -27x, x∈[-4,4];
(3)f(x)=6+12x-x , x∈[,3]; (4)f(x)=3x-x3. x∈[2,3];
课本P94 练习 1
课本P94 练习 2
2.证明不等式∶x-1≥lnx,x∈(0,+∞).
作业:课本P98 习题5.3 6
2.求f(x)在[a,b]上的最大值与最小值的步骤:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(思考:真的有必要去判断它是否是极值吗?)
(2)将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
小结
1.求最大(小)值的方法
只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值.
本小节结束
函数的最大(小)值
f (x)<0
y
x
O
x1
a
b
y=f(x)
极大值点两侧
极小值点两侧
f (x)<0
f (x)>0
f (x)>0
x2
结论:极值点处,f (x) =0
导数与极值的关系
求解函数极值的一般步骤:
(1)确定函数的定义域
(2)求函数的导数f ,(x)
(3)求方程f ,(x)=0的根
(4)用方程f ,(x)=0的根,顺次将函数的定义域分成 若干个开区间,并列成表格
(5)由f ,(x)在方程f ,(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况
(2) 由负变正,那么 是极小值点;
(3) 不变号,那么 不是极值点。
(1) 由正变负,那么 是极大值点;
由导函数图像判断极值
在社会生活实践中,为了发挥最大的经济效益,常常遇到如何能使用料最省、产量最高,效益最大等问题,这些问题的解决常常可转化为求一个函数的最大值和最小值问题
函数在什么条件下一定有最大、最小值?他们与函数极值关系如何?
极值是一个局部概念,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小。
问题导学:
3.求函数最值的一般方法
一是利用函数性质 二是利用不等式
三是利用导数
观察区间[a,b]上函数y=f (x)的图象,
你能找出它的极大值点,极小值点吗?
极大值点 ,
极小值点
你能说出函数的最大值点和最小值点吗?
最大值点 :a ,
最小值点:d
找出f (x)在区间[a,b]内的最值
找出f (x)在区间[a,b]内的最值
函数最值的概念
定义:可导函数 在闭区间[a,b]上所有点处的函数值中最大(或最小)值,叫做函数 的最大(或最小)值。
一般地,在闭区间上连续的函数
在[a,b]上必有最大值与最小值。
x
o
y
a
x1
b
y=f(x)
x2
x3
x4
x5
x6
x
o
y
a
x1
b
y=f(x)
x2
x3
x4
x5
x6
在开区间(a,b)内的连续函数不一定有最大值与最小值.
在闭区间[a,b]上的连续函数必有最大值与最小值
因此:该函数没有最大值.
f(x)max=f(a), f(x)min=f(x3)
·
·
思考:如何求出函数在[a,b]上的最值?
一般的如果在区间[a,b]上,函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
只要把函数y=f (x)的所有极值连同端点的函数值进行比较即可得到最大最小值。
一般地,利用导数求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下:
(2)将y=f(x)的各极值与端点处函数值f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(1)求f(x)在区间(a,b)内的极值(极大值或极小值)
例6: 求在[0,3]的最大值与最小值.
解:
由例5可知当x=2时有极小值,
1.求出所有导数为0的点;
2.计算端点值;
3.比较确定最值
例6: 求在[0,3]的最大值与最小值.
求函数y=f (x)在[a,b]上的最大值与最小值的步骤:
①求函数y=f (x)在(a,b)内的极值;
②将函数y=f (x)的各极值与端点处的函数值f (a), f (b)比较,其中最大的一个是最大值,最小的一个是最小值.
注意
1) 函数的最值概念是全局性的
2) 函数的最大值(最小值)唯一
3) 函数的最大值大于等于最小值
4) 函数的最值可在端点处取得
1.求下列函数的极值∶
(1)f(x)=6x -x-2,x∈[0,2]; (2)f(x)=x -27x, x∈[-4,4];
(3)f(x)=6+12x-x , x∈[,3]; (4)f(x)=3x-x3. x∈[2,3];
课本P94 练习 1
课本P94 练习 2
2.证明不等式∶x-1≥lnx,x∈(0,+∞).
作业:课本P98 习题5.3 6
2.求f(x)在[a,b]上的最大值与最小值的步骤:
(1)f(x)在(a,b)内导函数为零的点,并计算出其函数值;
(思考:真的有必要去判断它是否是极值吗?)
(2)将f(x)的各导数值为零的点的函数值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
小结
1.求最大(小)值的方法
只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值和最小值.
本小节结束
