6.4.3.3余弦定理、正弦定理应用举例(第一课时)课件-2021-2022学年高一下学期数学人教A版必修第二册(24张ppt)
文档属性
| 名称 | 6.4.3.3余弦定理、正弦定理应用举例(第一课时)课件-2021-2022学年高一下学期数学人教A版必修第二册(24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
第6章平面向量及其应用
6.4平面向量的应用
6.4.3余弦定理、正弦定理
6.4.3.3余弦定理、正弦定理应用举例(第一课时)
教学目标
1、理解实际测量问题中的有关名词、术语(基线、仰角等)的确切含义
2、能利用正余弦定理解决实践中的有关距离问
3、能利用正余弦定理解决实践中的有关高度问题,
复习:
N
a2 =b2+c2-2bccos A;
余弦定理:
c2 a2+62-2abcos C.
b2 a2 +b2-2ac cos B;
a
b
C
正弦定理:
sin 4
sin B sin C
正弦定理的变式:
a=2Rsin A,b=2Rsin B,c=2Rsin C
创设情境,引入主题
在实践中,我们经常会遇到测量距离、高度、角度等实际问题.解决
这类问题,通常需要借助经纬仪以及卷尺等测量角和距离的工具进行测
量
具体测量时,我们常常遇到“不能到达”的困难,这就需要设计恰
当的测量方案,下面我们通过几道例题来说明这种情况.需要注意的
是,题中为什么要给出这些已知条件,而不是其他条件
事实上,这些条件往往隐含着相应测量问题在某种特定情景和条件
限制下的一个测量方案,而且是这种情景与条件限制下的恰当方案
思考一
1、现实生活中,人们是怎祥测量底部不可到达的建
筑物的高度呢?又怎样在水平飞行的飞机上测量飞机下
方山顶的海拔高度呢?
2、在实际的航海生活中,人们也会遇到如下的问
题:在浩瀚的海面上如何确保轮船不迷失方向,保持一
定的航速和航向呢?
合作探究,形成新知
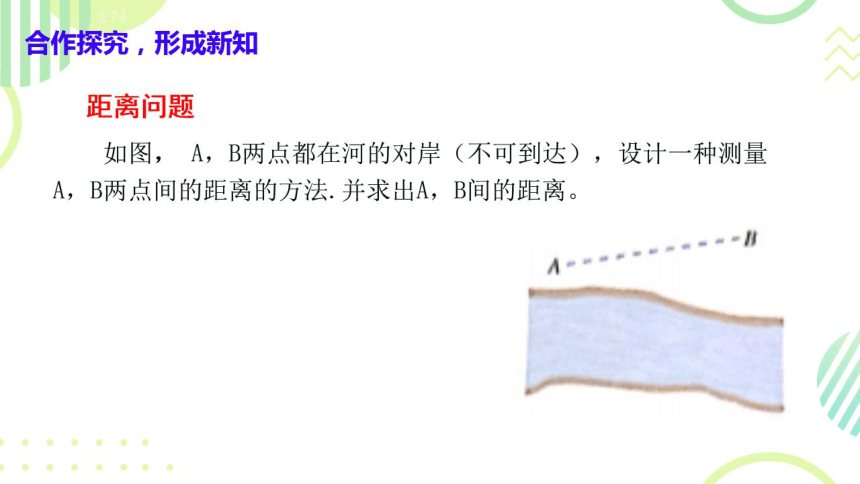
距离问题
如图,A,B两点都在河的对岸(不可到达),设计一种测量
A,B两点间的距离的方法.并求出A,B间的距离。
分析:若测量者在A,B两点的对岸取定一点C(称作测量基点),则在点C处
只能测出∠ACB的大小,因而无法解决问题.为此,可以再取一点D,测出线段CD
的长,以及∠ACD,∠CDB,∠BDA,这样就可借助正弦和余弦定理算出距离了.
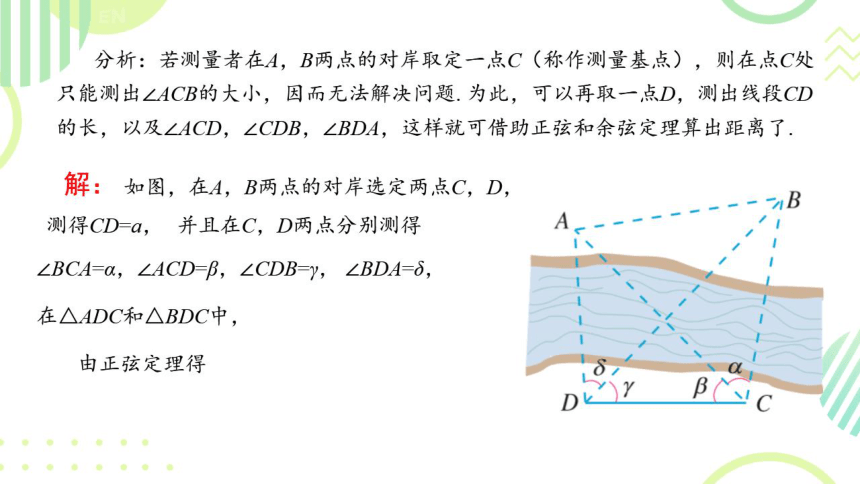
解:如图,在A,B两点的对岸选定两点C,D,
测得CD=a,并且在C,D两点分别测得
∠BCA=Oa,∠ACD=B,∠CDB=Y,∠BDA=δ,
在△ADC和△BDC中,
由正弦定理得
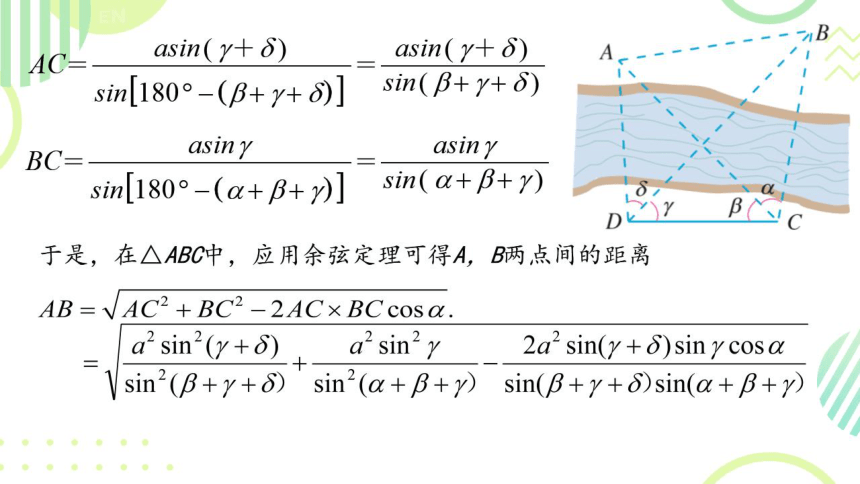
AC=
asin(y+δ)
asin(y+)
sin[180°-(B+y+6)]
sin(B+y+δ)
BC=
asin y
asiny
sin[180°-(a+B+y)]
sin(a+B+y)
于是,在△ABC中,应用余弦定理可得A,B两点间的距离
AB=AC2+BC2-2ACx BC cosa.
a2sin2(y+δ)
a2sin2y
2a2sin(y+δ)siny cosa
sin2(B+y+5)sin2(a+B+y)sin(B+y+8)sin(+B+y
第6章平面向量及其应用
6.4平面向量的应用
6.4.3余弦定理、正弦定理
6.4.3.3余弦定理、正弦定理应用举例(第一课时)
教学目标
1、理解实际测量问题中的有关名词、术语(基线、仰角等)的确切含义
2、能利用正余弦定理解决实践中的有关距离问
3、能利用正余弦定理解决实践中的有关高度问题,
复习:
N
a2 =b2+c2-2bccos A;
余弦定理:
c2 a2+62-2abcos C.
b2 a2 +b2-2ac cos B;
a
b
C
正弦定理:
sin 4
sin B sin C
正弦定理的变式:
a=2Rsin A,b=2Rsin B,c=2Rsin C
创设情境,引入主题
在实践中,我们经常会遇到测量距离、高度、角度等实际问题.解决
这类问题,通常需要借助经纬仪以及卷尺等测量角和距离的工具进行测
量
具体测量时,我们常常遇到“不能到达”的困难,这就需要设计恰
当的测量方案,下面我们通过几道例题来说明这种情况.需要注意的
是,题中为什么要给出这些已知条件,而不是其他条件
事实上,这些条件往往隐含着相应测量问题在某种特定情景和条件
限制下的一个测量方案,而且是这种情景与条件限制下的恰当方案
思考一
1、现实生活中,人们是怎祥测量底部不可到达的建
筑物的高度呢?又怎样在水平飞行的飞机上测量飞机下
方山顶的海拔高度呢?
2、在实际的航海生活中,人们也会遇到如下的问
题:在浩瀚的海面上如何确保轮船不迷失方向,保持一
定的航速和航向呢?
合作探究,形成新知
距离问题
如图,A,B两点都在河的对岸(不可到达),设计一种测量
A,B两点间的距离的方法.并求出A,B间的距离。
分析:若测量者在A,B两点的对岸取定一点C(称作测量基点),则在点C处
只能测出∠ACB的大小,因而无法解决问题.为此,可以再取一点D,测出线段CD
的长,以及∠ACD,∠CDB,∠BDA,这样就可借助正弦和余弦定理算出距离了.
解:如图,在A,B两点的对岸选定两点C,D,
测得CD=a,并且在C,D两点分别测得
∠BCA=Oa,∠ACD=B,∠CDB=Y,∠BDA=δ,
在△ADC和△BDC中,
由正弦定理得
AC=
asin(y+δ)
asin(y+)
sin[180°-(B+y+6)]
sin(B+y+δ)
BC=
asin y
asiny
sin[180°-(a+B+y)]
sin(a+B+y)
于是,在△ABC中,应用余弦定理可得A,B两点间的距离
AB=AC2+BC2-2ACx BC cosa.
a2sin2(y+δ)
a2sin2y
2a2sin(y+δ)siny cosa
sin2(B+y+5)sin2(a+B+y)sin(B+y+8)sin(+B+y
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
