7.1复数的概念(PPT)-2021-2022学年高一数学同步备课 (人教A版2019 必修第二册)(16张ppt)
文档属性
| 名称 | 7.1复数的概念(PPT)-2021-2022学年高一数学同步备课 (人教A版2019 必修第二册)(16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 780.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 22:04:05 | ||
图片预览






文档简介
(共16张PPT)
第七章 复数
7.1 复数的概念
教材分析
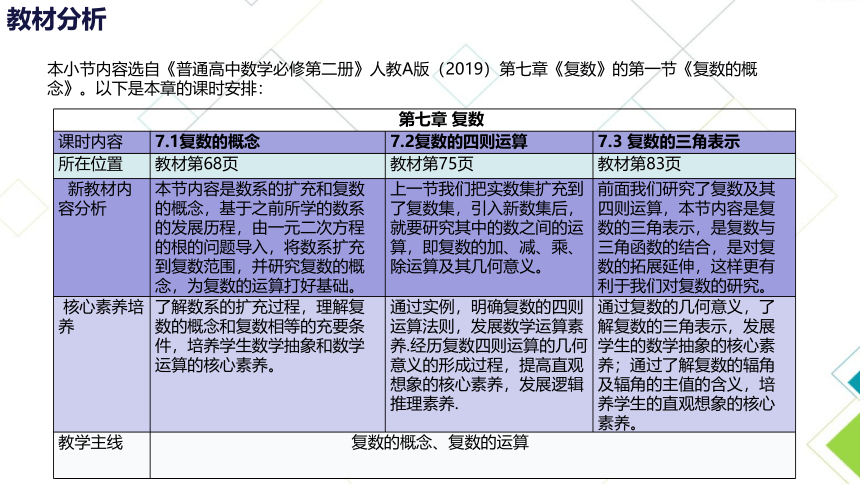
本小节内容选自《普通高中数学必修第二册》人教A版(2019)第七章《复数》的第一节《复数的概念》。以下是本章的课时安排:
第七章 复数
课时内容 7.1复数的概念 7.2复数的四则运算 7.3 复数的三角表示
所在位置 教材第68页 教材第75页 教材第83页
新教材内容分析 本节内容是数系的扩充和复数的概念,基于之前所学的数系的发展历程,由一元二次方程的根的问题导入,将数系扩充到复数范围,并研究复数的概念,为复数的运算打好基础。 上一节我们把实数集扩充到了复数集,引入新数集后,就要研究其中的数之间的运算,即复数的加、减、乘、除运算及其几何意义。 前面我们研究了复数及其四则运算,本节内容是复数的三角表示,是复数与三角函数的结合,是对复数的拓展延伸,这样更有利于我们对复数的研究。
核心素养培养 了解数系的扩充过程,理解复数的概念和复数相等的充要条件,培养学生数学抽象和数学运算的核心素养。 通过实例,明确复数的四则运算法则,发展数学运算素养.经历复数四则运算的几何意义的形成过程,提高直观想象的核心素养,发展逻辑推理素养. 通过复数的几何意义,了解复数的三角表示,发展学生的数学抽象的核心素养;通过了解复数的辐角及辐角的主值的含义,培养学生的直观想象的核心素养。
教学主线 复数的概念、复数的运算
学习目标
1.了解引进虚数单位的必要性,了解数系的扩充过程,培养数学抽象的核心素养;
2.理解在数系的扩充中由实数集扩展到复数集出现的一些基本概念,培养数学抽象的核心素养;
3.掌握复数代数形式的表示方法,理解复数相等的充要条件,培养数学运算的核心素养。
重点、难点
1.重点:了解引进虚数单位的必要性,了解数系的扩充过程;
掌握复数的分类及复数相等的充要条件。
2.难点:理解复数的概念、表示法及相关概念。
(一)新知导入
1. 复数的发展史
1545年,意大利数学家、物理学家卡尔丹在其所著《重要的艺术》一书中提出将10分成两部分,使其积为40的问题,即求方程x(10-x)=40的根,他求出的根为5+和5-,积为25-(-15)=40.
但由于这只是单纯从形式上推广而来,并且人们原先就已断言负数开平方是没有意义的.因此复数在历史上长期不被接受.
直到18世纪,达朗贝尔、欧拉和高斯等人逐步阐明了复数的几何意义及物理意义,建立了系统的复数理论,从而使人们终于接受并理解了复数.复变函数的理论基础是在19世纪奠定的,主要是围绕柯西、魏尔斯特拉斯和黎曼三人的工作进行的.
到本世纪,复变函数论是数学的重要分支之一,随着它的领域不断扩大而发展成一门庞大的学科,在自然科学的其他分支(如空气动力学、流体力学、电学、热学、理论物理等)及数学的其他分支(如微分方程、积分方程、概率论、数论等)中,复变函数论都有着重要应用.
(一)新知导入
2.探索交流,解决问题
【思考1】在实数范围内,方程x2+2=0有解吗?怎样让它有解?
【提示】无解.在复数的范围内,方程有解。
【思考2】为了使负数能够开方,需要引进一个新数,这个新数应该服从什么规则?
【提示】根据数系扩充的原则,定义关于它们的加法和乘法,要使得原来关于实数的运算律保持不变.
(二)复数的概念
1.复数的有关概念
(1)定义:形如 的数叫做复数,其中 i 叫做虚数单位,满足 .全体复数所构成的集合C={a+bi|a,b∈R}叫做 .
(2)复数通常用字母z表示,代数形式为z= (a,b∈R),其中a与b分别叫做复数z的 与 .
【做一做】指出复数 的实部和虚部。
实部a、虚部b 都是实数!
a+bi(a,b∈R)
i2=-1
复数集
a+bi
实部
虚部
(二)复数的概念
2.复数相等
在复数集C={a+bi|a,b∈R}中任取两个数a+bi,c+di(a,b,c,d∈R),我们规定:a+bi与c+di相等当且仅当 .
【做一做】 若(x-2y)i=2x+1+3i,则实数x,y的值分别为________.
答案:- -
a=c且b=d
(二)复数的概念
3.复数的分类
(1)对于复数a+bi(a,b∈R),当且仅当b=0时,它是 ;当且仅当a=b=0时,它是实数0;当b≠0时,叫做 ;当 时,叫做纯虚数.
(2)集合表示:
【思考1】两个复数一定能比较大小吗?
【提示】不一定,只有当这两个复数是实数时,才能比较大小.
【思考2】复数z=a+bi的虚部b可以为零吗?
【提示】可以.当b=0时,z为实数.
【辩一辩】判断(正确的打“√”,错误的打“×”)
(1)若a,b为实数,则z=a+bi为虚数.( )
(2)复数z1=3i,z2=2i,则z1>z2.( )
(3)复数z=bi是纯虚数.( )
(4)实数集与复数集的交集是实数集.( )
×
×
×
√
a=0且b≠0
实数
虚数
(三)典型例题
1.复数的概念
例1.以2i-5的虚部为实部,以+2i的实部为虚部的复数是________.
【类题通法】复数a+bi(a,b∈R)中,实数a和b分别叫做复数的实部和虚部.特别注意,b为复数的虚部而不是虚部的系数,b连同它的符号叫做复数的虚部.
【巩固练习1】下列命题中,正确命题的个数是( )
①若x,y∈C,则x+yi=1+i的充要条件是x=y=1;
②若a,b∈R且a>b,则a+i>b+i;
③若x2+y2=0,则x=y=0.
A.0 B.1 C.2 D.3
解析 ①由于x,y∈C,所以x+yi不一定是复数的代数形式,不符合复数相等的充要条件,所以①是假命题.②由于两个虚数不能比较大小,所以②是假命题.③当x=1,y=i时,x2+y2=0成立,所以③是假命题.故选A.
答案 A
【解析】2i-5的虚部为2,+2i的实部为,所以新的复数是2+i.
答案:2+i
(三)典型例题
2.复数的分类
例2. (1)已知复数z=a+(a2-1)i是实数,则实数a的值为________;
(2)若复数z=sin 2α-(1-cos 2α)i是纯虚数,则α=________.
解析 (1)∵z是实数,∴a2-1=0,∴a=±1.
(2)由题意知sin 2α=0,1-cos 2α≠0,
∴2α=2kπ+π(k∈Z),∴α=kπ+(k∈Z).
答案 (1)±1 (2)kπ+(k∈Z)
【类题通法】根据复数的概念求参数的一般步骤:
第一步,判定复数是否为a+bi(a,b∈R)的形式,实部与虚部分别为什么;
第二步,依据复数的有关概念将复数问题转化为实数问题;
第三步,解相应的方程(组)或不等式(组);
第四步,明确结论.
(三)典型例题
【巩固练习2】实数m取什么值时,复数z=+(m2-2m)i是
(1)实数;(2)虚数;(3)纯虚数?
解 (1)当, 即m=2时,复数z是实数.
(2)当,即m≠0且m≠2时,复数z是虚数.
(3)当, 即m=-3时,复数z是纯虚数.
(三)典型例题
3.复数相等
例3.已知x2-y2+2xyi=2i,求实数x,y的值.
解 ∵x2-y2+2xyi=2i,
∴解 得 或
【类题通法】求解复数相等问题
复数问题实数化是解决复数相等问题最基本的也是最重要的思想方法.转化过程主要依据复数相等的充要条件.基本思路是:
(1)等式两边整理为a+bi(a,b∈R)的形式;
(2)由复数相等的充要条件可以得到由两个实数等式所组成的方程组;
(3)解方程组,求出相应的参数.
【巩固练习3】关于x的方程3x--1=(10-x)i有实根,求实数a的值.
解 设方程的实数根为x=m,则原方程可变为3m--1=(10-m)i,所以
∴解得a=58.
(四)操作演练 素养提升
1.已知复数z=a2-(2-b)i的实部和虚部分别是2和3,则实数a,b的值分别是( )
A.,1 B. ,5
C.±,5 D.±,1
2.下列复数中,满足方程x2+2=0的是( )
A.±1 B.±i
C.±i D.±2i
3.i2021=________.
4.设i为虚数单位,若关于x的方程x2-(2+i)x+1+mi=0(m∈R)有一实根为n,则m=________.
答案:1.C 2.C 3.i 4.1
课堂小结
知识总结
学生反思
(1)通过这节课,你学到了什么知识?
(2)在解决问题时,用到了哪些数学思想?
作业布置
完成教材—— 第70页 练习 第1,2,3题
第73 页 习题7.1 第1,2,3题
不积跬步,无以至千里;
不积小流,无以成江海。
第七章 复数
7.1 复数的概念
教材分析
本小节内容选自《普通高中数学必修第二册》人教A版(2019)第七章《复数》的第一节《复数的概念》。以下是本章的课时安排:
第七章 复数
课时内容 7.1复数的概念 7.2复数的四则运算 7.3 复数的三角表示
所在位置 教材第68页 教材第75页 教材第83页
新教材内容分析 本节内容是数系的扩充和复数的概念,基于之前所学的数系的发展历程,由一元二次方程的根的问题导入,将数系扩充到复数范围,并研究复数的概念,为复数的运算打好基础。 上一节我们把实数集扩充到了复数集,引入新数集后,就要研究其中的数之间的运算,即复数的加、减、乘、除运算及其几何意义。 前面我们研究了复数及其四则运算,本节内容是复数的三角表示,是复数与三角函数的结合,是对复数的拓展延伸,这样更有利于我们对复数的研究。
核心素养培养 了解数系的扩充过程,理解复数的概念和复数相等的充要条件,培养学生数学抽象和数学运算的核心素养。 通过实例,明确复数的四则运算法则,发展数学运算素养.经历复数四则运算的几何意义的形成过程,提高直观想象的核心素养,发展逻辑推理素养. 通过复数的几何意义,了解复数的三角表示,发展学生的数学抽象的核心素养;通过了解复数的辐角及辐角的主值的含义,培养学生的直观想象的核心素养。
教学主线 复数的概念、复数的运算
学习目标
1.了解引进虚数单位的必要性,了解数系的扩充过程,培养数学抽象的核心素养;
2.理解在数系的扩充中由实数集扩展到复数集出现的一些基本概念,培养数学抽象的核心素养;
3.掌握复数代数形式的表示方法,理解复数相等的充要条件,培养数学运算的核心素养。
重点、难点
1.重点:了解引进虚数单位的必要性,了解数系的扩充过程;
掌握复数的分类及复数相等的充要条件。
2.难点:理解复数的概念、表示法及相关概念。
(一)新知导入
1. 复数的发展史
1545年,意大利数学家、物理学家卡尔丹在其所著《重要的艺术》一书中提出将10分成两部分,使其积为40的问题,即求方程x(10-x)=40的根,他求出的根为5+和5-,积为25-(-15)=40.
但由于这只是单纯从形式上推广而来,并且人们原先就已断言负数开平方是没有意义的.因此复数在历史上长期不被接受.
直到18世纪,达朗贝尔、欧拉和高斯等人逐步阐明了复数的几何意义及物理意义,建立了系统的复数理论,从而使人们终于接受并理解了复数.复变函数的理论基础是在19世纪奠定的,主要是围绕柯西、魏尔斯特拉斯和黎曼三人的工作进行的.
到本世纪,复变函数论是数学的重要分支之一,随着它的领域不断扩大而发展成一门庞大的学科,在自然科学的其他分支(如空气动力学、流体力学、电学、热学、理论物理等)及数学的其他分支(如微分方程、积分方程、概率论、数论等)中,复变函数论都有着重要应用.
(一)新知导入
2.探索交流,解决问题
【思考1】在实数范围内,方程x2+2=0有解吗?怎样让它有解?
【提示】无解.在复数的范围内,方程有解。
【思考2】为了使负数能够开方,需要引进一个新数,这个新数应该服从什么规则?
【提示】根据数系扩充的原则,定义关于它们的加法和乘法,要使得原来关于实数的运算律保持不变.
(二)复数的概念
1.复数的有关概念
(1)定义:形如 的数叫做复数,其中 i 叫做虚数单位,满足 .全体复数所构成的集合C={a+bi|a,b∈R}叫做 .
(2)复数通常用字母z表示,代数形式为z= (a,b∈R),其中a与b分别叫做复数z的 与 .
【做一做】指出复数 的实部和虚部。
实部a、虚部b 都是实数!
a+bi(a,b∈R)
i2=-1
复数集
a+bi
实部
虚部
(二)复数的概念
2.复数相等
在复数集C={a+bi|a,b∈R}中任取两个数a+bi,c+di(a,b,c,d∈R),我们规定:a+bi与c+di相等当且仅当 .
【做一做】 若(x-2y)i=2x+1+3i,则实数x,y的值分别为________.
答案:- -
a=c且b=d
(二)复数的概念
3.复数的分类
(1)对于复数a+bi(a,b∈R),当且仅当b=0时,它是 ;当且仅当a=b=0时,它是实数0;当b≠0时,叫做 ;当 时,叫做纯虚数.
(2)集合表示:
【思考1】两个复数一定能比较大小吗?
【提示】不一定,只有当这两个复数是实数时,才能比较大小.
【思考2】复数z=a+bi的虚部b可以为零吗?
【提示】可以.当b=0时,z为实数.
【辩一辩】判断(正确的打“√”,错误的打“×”)
(1)若a,b为实数,则z=a+bi为虚数.( )
(2)复数z1=3i,z2=2i,则z1>z2.( )
(3)复数z=bi是纯虚数.( )
(4)实数集与复数集的交集是实数集.( )
×
×
×
√
a=0且b≠0
实数
虚数
(三)典型例题
1.复数的概念
例1.以2i-5的虚部为实部,以+2i的实部为虚部的复数是________.
【类题通法】复数a+bi(a,b∈R)中,实数a和b分别叫做复数的实部和虚部.特别注意,b为复数的虚部而不是虚部的系数,b连同它的符号叫做复数的虚部.
【巩固练习1】下列命题中,正确命题的个数是( )
①若x,y∈C,则x+yi=1+i的充要条件是x=y=1;
②若a,b∈R且a>b,则a+i>b+i;
③若x2+y2=0,则x=y=0.
A.0 B.1 C.2 D.3
解析 ①由于x,y∈C,所以x+yi不一定是复数的代数形式,不符合复数相等的充要条件,所以①是假命题.②由于两个虚数不能比较大小,所以②是假命题.③当x=1,y=i时,x2+y2=0成立,所以③是假命题.故选A.
答案 A
【解析】2i-5的虚部为2,+2i的实部为,所以新的复数是2+i.
答案:2+i
(三)典型例题
2.复数的分类
例2. (1)已知复数z=a+(a2-1)i是实数,则实数a的值为________;
(2)若复数z=sin 2α-(1-cos 2α)i是纯虚数,则α=________.
解析 (1)∵z是实数,∴a2-1=0,∴a=±1.
(2)由题意知sin 2α=0,1-cos 2α≠0,
∴2α=2kπ+π(k∈Z),∴α=kπ+(k∈Z).
答案 (1)±1 (2)kπ+(k∈Z)
【类题通法】根据复数的概念求参数的一般步骤:
第一步,判定复数是否为a+bi(a,b∈R)的形式,实部与虚部分别为什么;
第二步,依据复数的有关概念将复数问题转化为实数问题;
第三步,解相应的方程(组)或不等式(组);
第四步,明确结论.
(三)典型例题
【巩固练习2】实数m取什么值时,复数z=+(m2-2m)i是
(1)实数;(2)虚数;(3)纯虚数?
解 (1)当, 即m=2时,复数z是实数.
(2)当,即m≠0且m≠2时,复数z是虚数.
(3)当, 即m=-3时,复数z是纯虚数.
(三)典型例题
3.复数相等
例3.已知x2-y2+2xyi=2i,求实数x,y的值.
解 ∵x2-y2+2xyi=2i,
∴解 得 或
【类题通法】求解复数相等问题
复数问题实数化是解决复数相等问题最基本的也是最重要的思想方法.转化过程主要依据复数相等的充要条件.基本思路是:
(1)等式两边整理为a+bi(a,b∈R)的形式;
(2)由复数相等的充要条件可以得到由两个实数等式所组成的方程组;
(3)解方程组,求出相应的参数.
【巩固练习3】关于x的方程3x--1=(10-x)i有实根,求实数a的值.
解 设方程的实数根为x=m,则原方程可变为3m--1=(10-m)i,所以
∴解得a=58.
(四)操作演练 素养提升
1.已知复数z=a2-(2-b)i的实部和虚部分别是2和3,则实数a,b的值分别是( )
A.,1 B. ,5
C.±,5 D.±,1
2.下列复数中,满足方程x2+2=0的是( )
A.±1 B.±i
C.±i D.±2i
3.i2021=________.
4.设i为虚数单位,若关于x的方程x2-(2+i)x+1+mi=0(m∈R)有一实根为n,则m=________.
答案:1.C 2.C 3.i 4.1
课堂小结
知识总结
学生反思
(1)通过这节课,你学到了什么知识?
(2)在解决问题时,用到了哪些数学思想?
作业布置
完成教材—— 第70页 练习 第1,2,3题
第73 页 习题7.1 第1,2,3题
不积跬步,无以至千里;
不积小流,无以成江海。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
