第6章 平面向量及其应用综合(PPT)-2021-2022学年高一数学同步备课 (人教A版2019 必修第二册)(19张ppt)
文档属性
| 名称 | 第6章 平面向量及其应用综合(PPT)-2021-2022学年高一数学同步备课 (人教A版2019 必修第二册)(19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 22:20:36 | ||
图片预览




文档简介
(共19张PPT)
第六章 平面向量及其应用
本章总结
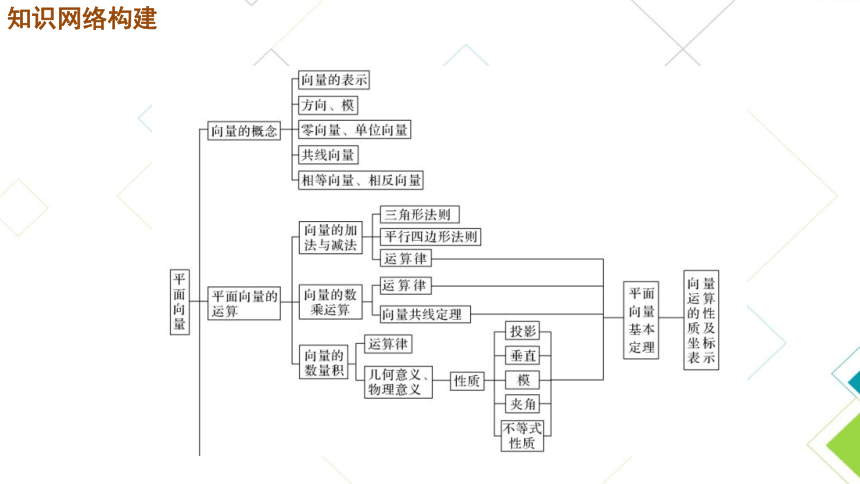
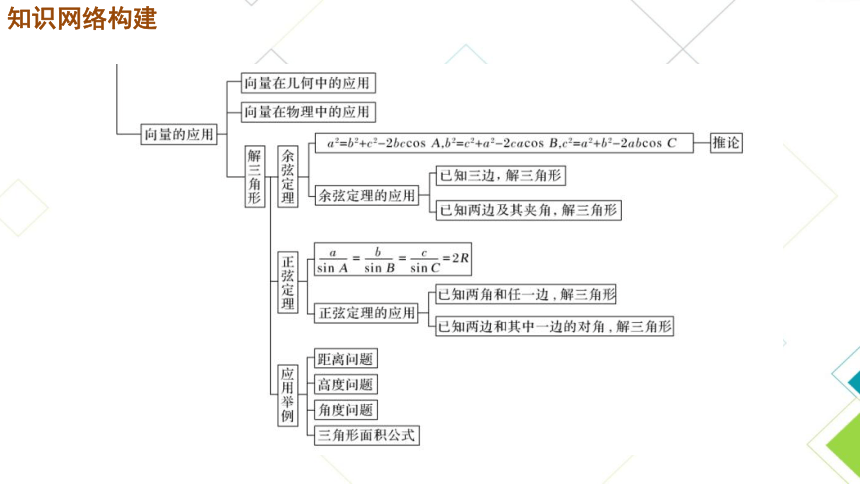
知识网络构建
知识网络构建
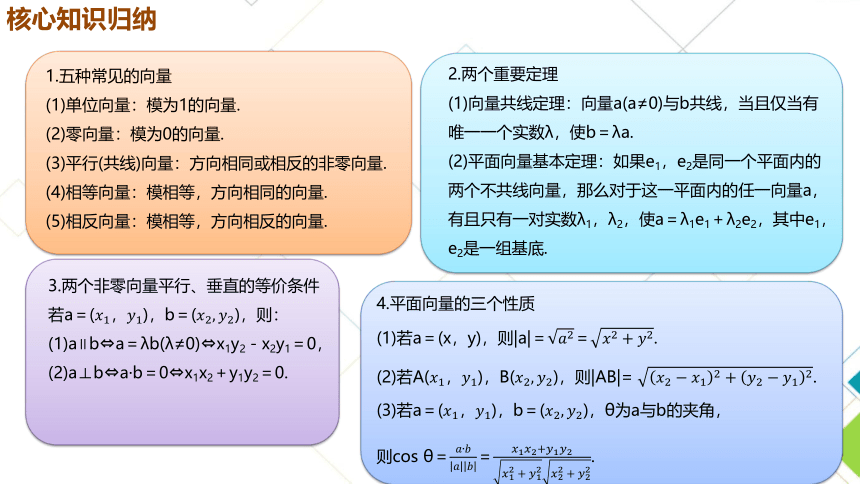
核心知识归纳
1.五种常见的向量
(1)单位向量:模为1的向量.
(2)零向量:模为0的向量.
(3)平行(共线)向量:方向相同或相反的非零向量.
(4)相等向量:模相等,方向相同的向量.
(5)相反向量:模相等,方向相反的向量.
2.两个重要定理
(1)向量共线定理:向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使b=λa.
(2)平面向量基本定理:如果e1,e2是同一个平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2,其中e1,e2是一组基底.
3.两个非零向量平行、垂直的等价条件
若a=(),b=(),则:
(1)a∥b a=λb(λ≠0) x1y2-x2y1=0,
(2)a⊥b a·b=0 x1x2+y1y2=0.
4.平面向量的三个性质
(1)若a=(x,y),则|a|==.
(2)若A(),B(),则|AB|.
(3)若a=(),b=(),θ为a与b的夹角,
则cos θ==.
三、典型例题
1.平面向量的线性运算及应用
【例1】 若D点在三角形ABC的边BC上,且=4=r+s,则3r+s的值为( )
A. B. C. D.
解析 因为=4=r+s,
所以= = ( - )=r +s ,
所以r=,s=-,所以3r+s=-=.
答案 C
【类题通法】向量线性运算的基本原则和求解策略
(1)基本原则:向量的加法、减法和数乘运算统称为向量的线性运算.向量的线性运算的结果仍是一个向量,因此,对它们的运算法则、运算律的理解和运用要注意向量的大小和方向两个方面.
(2)求解策略:①向量是一个有“形”的几何量,因此在进行向量线性运算时,一定要结合图形,这是研究平面向量的重要方法与技巧.
②字符表示下线性运算的常用技巧:
首尾相接用加法的三角形法则;共起点两个向量作差用减法的几何意义.
三、典型例题
【巩固训练1】 如图所示,正方形ABCD中,M是BC的中点,若 =λ +μ ,则λ+μ等于( )
A. B. C. D.2
【解析】因为=λ +μ =λ( + )+μ( + )
=λ+μ(- + )=(λ-μ)+,
且 = +,所以 得 ,所以λ+μ=,故选B.
答案 B
三、典型例题
2.向量的数量积
【例2】 已知a=(cos α,sin α),b=(cos β,sin β),且|ka+b|=|a-kb|(k>0).
(1)用k表示数量积a·b;
(2)求a·b的最小值,并求出此时a与b的夹角θ的大小.
解 (1)由|ka+b|=|a-kb|,得(ka+b)2=3(a-kb)2,
∴k2a2+2ka·b+b2=3a2-6ka·b+3k2b2. ∴(k2-3)a2+8ka·b+(1-3k2)b2=0.
∵|a|=1,|b|=1,∴k2-3+8ka·b+1-3k2=0,∴a·b==(k>0).
(2)a·b==.由对勾函数的单调性可知,f(k)=在(0,1]上单调递减,在[1,+∞)上单调递增,
∴当k=1时,f(k)min=f(1)=×(1+1)=,此时a与b的夹角θ的余弦值cos θ=,
又∵0°≤θ≤180°,∴θ=60°.
三、典型例题
【类题通法】数量积运算是向量运算的核心,利用向量数量积可以解决以下问题:
(1)设a=(),b=(),a∥b x1y2-x2y1=0,a⊥b x1x2+y1y2=0.
(2)求向量的夹角和模的问题
①设a=(),则|a|=. ②两向量夹角的余弦值(0≤θ≤π),cos θ=.
【巩固训练2】 已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则 · 的值为( )
A.- B. C. D.
解析 ∵ =-,=+ =+=+,
∴ · =(- )·(+) =
=×1×1-×1×1-×1×1×cos 60°=.
答案 B
三、典型例题
3. 平面向量在几何中的应用
【例3】 如图,半径为的扇形AOB的圆心角为120°,点C在上,且∠COB=30°,若 =λ +μ ,则λ+μ等于( )
A. B. C. D.2
解析 由题意,得∠AOC=90°,故以O为坐标原点,OC,OA所在直线分别为x轴,y轴建立平面直角坐标系,
则O(0,0),A(0,),C(,0),B(cos 30°,-sin 30°),
因为 =λ +μ ,所以(,0)=λ(0,)+μ,
即 , 则 ,所以λ+μ=.
答案 A
三、典型例题
【类题通法】把几何图形放到适当的坐标系中,就赋予了有关点与向量具体的坐标,这样就能进行相应的代数运算和向量运算,从而解决问题.这样的解题方法具有普遍性.
【巩固训练3】 在△ABC中,AB=AC,D为AB的中点,E为△ACD的重心,F为△ABC的外心,证明:EF⊥CD.
证明 建立如图所示的平面直角坐标系.
设A(0,b),B(-a,0),C(a,0),则D,= .
易知△ABC的外心F在y轴上,可设为(0,y).
由|AF|=|CF|,得(y-b)2=(-a)2+y2,所以y=,即F.
由重心坐标公式,得E,所以 = .
所以 · =×+×=0,所以 ⊥ ,即EF⊥CD.
三、典型例题
4. 利用余弦、正弦定理解三角形
【例4】 在△ABC中,内角A,B,C的对边分别为a,b,c,且bsin A=acos B.
(1)求角B的大小;
(2)若b=3,sin C=2sin A,求a,c的值.
解 (1)由bsin A=acos B及正弦定理 得sin B=cos B,
所以tan B=,又0(2)因为sin C=2sin A,由正弦定理得c=2a.
由b=3及余弦定理b2=a2+c2-2accos B,
得9=a2+c2-ac.
所以a=,c=2.
三、典型例题
【类题通法】1.已知三角形的任意两个角和一边,可结合三角形内角和定理及正弦定理解此三角形.
2.已知三角形的两边和其中一边的对角,这个三角形解的情况是不确定的.如已知△ABC的边长a,b和角A,根据正弦定理求角B时,可能出现一解、两解、无解的情况,这时应借助已知条件进行检验,务必做到不漏解、不多解.
【巩固训练4】 已知在△ABC中,角A,B,C的对应的边分别是a,b,c,且C=2A,a+c=10,cos A=,求b的值.
解 在△ABC中,由正弦定理得,===2cos A=,∴3a=2c.又a+c=10,所以a=4,c=6.
由余弦定理的推论得,cos A==,
代入数据化简得:b2-9b+20=0,∴b=4或b=5.
若b=4,而在△ABC中,a=4,∴△ABC为等腰三角形,且A=B,又C=2A,且A+B+C=180°,∴A=B=45°,C=90°,△ABC为等腰直角三角形,由勾股定理得c=4,这与已求出的c=6相矛盾,故要舍去.
经检验b=5满足题意.
三、典型例题
5. 余弦、正弦定理在实际问题中的应用
【例5】 如图,A,B是海面上位于东西方向相距5(3+) n mile的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20 n mile的C点的救援船立即前往营救,其航行速度为30 n mile/h,该救援船到达D点需要多长时间?
解 由题意知AB=5(3+) n mile,∠DBA=90°-60°=30°,
∠DAB=90°-45°=45°,∴∠ADB=180°-(45°+30°)=105°,
在△DAB中,由正弦定理得 =,∴DB===10(n mile),
又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC=20(n mile),
在△DBC中,由余弦定理得CD2=BD2+BC2-2BD·BC·cos ∠DBC=300+1 200-2×10×20×=900,
∴CD=30(n mile).则需要的时间t=1(h).
答:救援船到达D点需要1 h.
三、典型例题
【类题通法】正、余弦定理在实际生活中,有着非常广泛的应用,常见的问题涉及距离、高度、角度以及平面图形的面积等很多方面.解决这类问题,关键是根据题意画出示意图,将问题抽象为三角形的模型,然后利用定理求解.注意隐含条件和最后将结果还原为实际问题进行检验.
【巩固训练5】 如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31 km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20 km后到达D处,测得C,D两处的距离为21 km,这时此车距离A城多少千米?
解:在△BCD中,BC=31,BD=20,CD=21,
由余弦定理得,cos∠BDC===-,所以cos∠ADC=,sin∠ADC=.
在△ACD中,由条件知CD=21,A=60°,所以sin∠ACD=sin(60°+∠ADC)=.
由正弦定理,得 =,所以AD=×=15. 故这时此车距离A城15千米.
四、操作演练 素养提升
1.已知向量m=(λ+1,1),n=(λ+2,2),若(m+n)⊥(m-n),则λ=( )
A.-4 B.-3 C.-2 D.-1
【解析】因为m+n=(2λ+3,3),
m-n=(-1,-1),
且(m+n)⊥(m-n),
所以(m+n)·(m-n)=-2λ-3-3=0,
解得λ=-3.
2.如图,在梯形ABCD中,AB∥CD,AB=4,AD=3,CD=2,=2 .若 · =-3,则 · = .
【解析】因为 · =·
=-2- · =-3,所以· =。
四、操作演练 素养提升
3.如图所示,在△ABC中,= ,P是BN上的一点,若 =m + ,则实数m的值为 .
【解析】设 =λ ,
则 =+=- +m +
=(m-1)+ .
=+=-+ .
∵与共线,∴(m-1)+=0,
∴m=.
4.已知c=ma+nb,c=(-2,2),a⊥c,b与c的夹角为,b·c=-4,|a|=2,求实数m,n的值及a与b的夹角θ.
解:∵c=(-2,2),∴|c|=4.∵a⊥c,∴a·c=0.
∵b·c=|b||c|cos=|b|×4×=-4,
∴|b|=2.∵c=ma+nb,∴c2=ma·c+nb·c,
∴16=n×(-4),∴n=-4.
在c=ma+nb两边同乘以a,得0=8m-4a·b.①
在c=ma+nb两边同乘以b,得ma·b=12.②
由①②,得m=±,
∴a·b=±2,
∴cos θ==±,∴θ=或 .
四、操作演练 素养提升
5.如图,在△ABC中,∠B=,AB=8,点D在BC边上,CD=2,cos∠ADC=.
(1)求sin∠BAD;
(2)求BD,AC的长.
[解] (1)在△ADC中,因为cos∠ADC=,所以sin∠ADC=.
所以sin∠BAD=sin(∠ADC-∠B)=sin∠ADC cos B-cos∠ADC sin B
=×-×=.
(2)在△ABD中,由正弦定理,得BD===3.
在△ABC中,由余弦定理,得
AC2=AB2+BC2-2AB×BC×cos B=82+52-2×8×5×=49. 所以AC=7.
五、课堂小结,反思感悟
1.知识总结:
2.学生反思:
(1)通过这节课,你学到了什么知识?
( 2)在解决问题时,用到了哪些数学思想?
作业布置
完成教材—— 第59页 复习参考题6 第1,2,3,4,5,6,7,8,910,11,
12,13,14,15,16,17题
不积跬步,无以至千里;
不积小流,无以成江海。
第六章 平面向量及其应用
本章总结
知识网络构建
知识网络构建
核心知识归纳
1.五种常见的向量
(1)单位向量:模为1的向量.
(2)零向量:模为0的向量.
(3)平行(共线)向量:方向相同或相反的非零向量.
(4)相等向量:模相等,方向相同的向量.
(5)相反向量:模相等,方向相反的向量.
2.两个重要定理
(1)向量共线定理:向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使b=λa.
(2)平面向量基本定理:如果e1,e2是同一个平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2,其中e1,e2是一组基底.
3.两个非零向量平行、垂直的等价条件
若a=(),b=(),则:
(1)a∥b a=λb(λ≠0) x1y2-x2y1=0,
(2)a⊥b a·b=0 x1x2+y1y2=0.
4.平面向量的三个性质
(1)若a=(x,y),则|a|==.
(2)若A(),B(),则|AB|.
(3)若a=(),b=(),θ为a与b的夹角,
则cos θ==.
三、典型例题
1.平面向量的线性运算及应用
【例1】 若D点在三角形ABC的边BC上,且=4=r+s,则3r+s的值为( )
A. B. C. D.
解析 因为=4=r+s,
所以= = ( - )=r +s ,
所以r=,s=-,所以3r+s=-=.
答案 C
【类题通法】向量线性运算的基本原则和求解策略
(1)基本原则:向量的加法、减法和数乘运算统称为向量的线性运算.向量的线性运算的结果仍是一个向量,因此,对它们的运算法则、运算律的理解和运用要注意向量的大小和方向两个方面.
(2)求解策略:①向量是一个有“形”的几何量,因此在进行向量线性运算时,一定要结合图形,这是研究平面向量的重要方法与技巧.
②字符表示下线性运算的常用技巧:
首尾相接用加法的三角形法则;共起点两个向量作差用减法的几何意义.
三、典型例题
【巩固训练1】 如图所示,正方形ABCD中,M是BC的中点,若 =λ +μ ,则λ+μ等于( )
A. B. C. D.2
【解析】因为=λ +μ =λ( + )+μ( + )
=λ+μ(- + )=(λ-μ)+,
且 = +,所以 得 ,所以λ+μ=,故选B.
答案 B
三、典型例题
2.向量的数量积
【例2】 已知a=(cos α,sin α),b=(cos β,sin β),且|ka+b|=|a-kb|(k>0).
(1)用k表示数量积a·b;
(2)求a·b的最小值,并求出此时a与b的夹角θ的大小.
解 (1)由|ka+b|=|a-kb|,得(ka+b)2=3(a-kb)2,
∴k2a2+2ka·b+b2=3a2-6ka·b+3k2b2. ∴(k2-3)a2+8ka·b+(1-3k2)b2=0.
∵|a|=1,|b|=1,∴k2-3+8ka·b+1-3k2=0,∴a·b==(k>0).
(2)a·b==.由对勾函数的单调性可知,f(k)=在(0,1]上单调递减,在[1,+∞)上单调递增,
∴当k=1时,f(k)min=f(1)=×(1+1)=,此时a与b的夹角θ的余弦值cos θ=,
又∵0°≤θ≤180°,∴θ=60°.
三、典型例题
【类题通法】数量积运算是向量运算的核心,利用向量数量积可以解决以下问题:
(1)设a=(),b=(),a∥b x1y2-x2y1=0,a⊥b x1x2+y1y2=0.
(2)求向量的夹角和模的问题
①设a=(),则|a|=. ②两向量夹角的余弦值(0≤θ≤π),cos θ=.
【巩固训练2】 已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则 · 的值为( )
A.- B. C. D.
解析 ∵ =-,=+ =+=+,
∴ · =(- )·(+) =
=×1×1-×1×1-×1×1×cos 60°=.
答案 B
三、典型例题
3. 平面向量在几何中的应用
【例3】 如图,半径为的扇形AOB的圆心角为120°,点C在上,且∠COB=30°,若 =λ +μ ,则λ+μ等于( )
A. B. C. D.2
解析 由题意,得∠AOC=90°,故以O为坐标原点,OC,OA所在直线分别为x轴,y轴建立平面直角坐标系,
则O(0,0),A(0,),C(,0),B(cos 30°,-sin 30°),
因为 =λ +μ ,所以(,0)=λ(0,)+μ,
即 , 则 ,所以λ+μ=.
答案 A
三、典型例题
【类题通法】把几何图形放到适当的坐标系中,就赋予了有关点与向量具体的坐标,这样就能进行相应的代数运算和向量运算,从而解决问题.这样的解题方法具有普遍性.
【巩固训练3】 在△ABC中,AB=AC,D为AB的中点,E为△ACD的重心,F为△ABC的外心,证明:EF⊥CD.
证明 建立如图所示的平面直角坐标系.
设A(0,b),B(-a,0),C(a,0),则D,= .
易知△ABC的外心F在y轴上,可设为(0,y).
由|AF|=|CF|,得(y-b)2=(-a)2+y2,所以y=,即F.
由重心坐标公式,得E,所以 = .
所以 · =×+×=0,所以 ⊥ ,即EF⊥CD.
三、典型例题
4. 利用余弦、正弦定理解三角形
【例4】 在△ABC中,内角A,B,C的对边分别为a,b,c,且bsin A=acos B.
(1)求角B的大小;
(2)若b=3,sin C=2sin A,求a,c的值.
解 (1)由bsin A=acos B及正弦定理 得sin B=cos B,
所以tan B=,又0
由b=3及余弦定理b2=a2+c2-2accos B,
得9=a2+c2-ac.
所以a=,c=2.
三、典型例题
【类题通法】1.已知三角形的任意两个角和一边,可结合三角形内角和定理及正弦定理解此三角形.
2.已知三角形的两边和其中一边的对角,这个三角形解的情况是不确定的.如已知△ABC的边长a,b和角A,根据正弦定理求角B时,可能出现一解、两解、无解的情况,这时应借助已知条件进行检验,务必做到不漏解、不多解.
【巩固训练4】 已知在△ABC中,角A,B,C的对应的边分别是a,b,c,且C=2A,a+c=10,cos A=,求b的值.
解 在△ABC中,由正弦定理得,===2cos A=,∴3a=2c.又a+c=10,所以a=4,c=6.
由余弦定理的推论得,cos A==,
代入数据化简得:b2-9b+20=0,∴b=4或b=5.
若b=4,而在△ABC中,a=4,∴△ABC为等腰三角形,且A=B,又C=2A,且A+B+C=180°,∴A=B=45°,C=90°,△ABC为等腰直角三角形,由勾股定理得c=4,这与已求出的c=6相矛盾,故要舍去.
经检验b=5满足题意.
三、典型例题
5. 余弦、正弦定理在实际问题中的应用
【例5】 如图,A,B是海面上位于东西方向相距5(3+) n mile的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20 n mile的C点的救援船立即前往营救,其航行速度为30 n mile/h,该救援船到达D点需要多长时间?
解 由题意知AB=5(3+) n mile,∠DBA=90°-60°=30°,
∠DAB=90°-45°=45°,∴∠ADB=180°-(45°+30°)=105°,
在△DAB中,由正弦定理得 =,∴DB===10(n mile),
又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC=20(n mile),
在△DBC中,由余弦定理得CD2=BD2+BC2-2BD·BC·cos ∠DBC=300+1 200-2×10×20×=900,
∴CD=30(n mile).则需要的时间t=1(h).
答:救援船到达D点需要1 h.
三、典型例题
【类题通法】正、余弦定理在实际生活中,有着非常广泛的应用,常见的问题涉及距离、高度、角度以及平面图形的面积等很多方面.解决这类问题,关键是根据题意画出示意图,将问题抽象为三角形的模型,然后利用定理求解.注意隐含条件和最后将结果还原为实际问题进行检验.
【巩固训练5】 如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31 km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20 km后到达D处,测得C,D两处的距离为21 km,这时此车距离A城多少千米?
解:在△BCD中,BC=31,BD=20,CD=21,
由余弦定理得,cos∠BDC===-,所以cos∠ADC=,sin∠ADC=.
在△ACD中,由条件知CD=21,A=60°,所以sin∠ACD=sin(60°+∠ADC)=.
由正弦定理,得 =,所以AD=×=15. 故这时此车距离A城15千米.
四、操作演练 素养提升
1.已知向量m=(λ+1,1),n=(λ+2,2),若(m+n)⊥(m-n),则λ=( )
A.-4 B.-3 C.-2 D.-1
【解析】因为m+n=(2λ+3,3),
m-n=(-1,-1),
且(m+n)⊥(m-n),
所以(m+n)·(m-n)=-2λ-3-3=0,
解得λ=-3.
2.如图,在梯形ABCD中,AB∥CD,AB=4,AD=3,CD=2,=2 .若 · =-3,则 · = .
【解析】因为 · =·
=-2- · =-3,所以· =。
四、操作演练 素养提升
3.如图所示,在△ABC中,= ,P是BN上的一点,若 =m + ,则实数m的值为 .
【解析】设 =λ ,
则 =+=- +m +
=(m-1)+ .
=+=-+ .
∵与共线,∴(m-1)+=0,
∴m=.
4.已知c=ma+nb,c=(-2,2),a⊥c,b与c的夹角为,b·c=-4,|a|=2,求实数m,n的值及a与b的夹角θ.
解:∵c=(-2,2),∴|c|=4.∵a⊥c,∴a·c=0.
∵b·c=|b||c|cos=|b|×4×=-4,
∴|b|=2.∵c=ma+nb,∴c2=ma·c+nb·c,
∴16=n×(-4),∴n=-4.
在c=ma+nb两边同乘以a,得0=8m-4a·b.①
在c=ma+nb两边同乘以b,得ma·b=12.②
由①②,得m=±,
∴a·b=±2,
∴cos θ==±,∴θ=或 .
四、操作演练 素养提升
5.如图,在△ABC中,∠B=,AB=8,点D在BC边上,CD=2,cos∠ADC=.
(1)求sin∠BAD;
(2)求BD,AC的长.
[解] (1)在△ADC中,因为cos∠ADC=,所以sin∠ADC=.
所以sin∠BAD=sin(∠ADC-∠B)=sin∠ADC cos B-cos∠ADC sin B
=×-×=.
(2)在△ABD中,由正弦定理,得BD===3.
在△ABC中,由余弦定理,得
AC2=AB2+BC2-2AB×BC×cos B=82+52-2×8×5×=49. 所以AC=7.
五、课堂小结,反思感悟
1.知识总结:
2.学生反思:
(1)通过这节课,你学到了什么知识?
( 2)在解决问题时,用到了哪些数学思想?
作业布置
完成教材—— 第59页 复习参考题6 第1,2,3,4,5,6,7,8,910,11,
12,13,14,15,16,17题
不积跬步,无以至千里;
不积小流,无以成江海。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
