青岛版小学五年级上册数学第五单元《回顾整理》教学课件(共34张PPT)
文档属性
| 名称 | 青岛版小学五年级上册数学第五单元《回顾整理》教学课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1011.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 11:17:58 | ||
图片预览






文档简介
(共34张PPT)
多边形的面积
——回顾整理
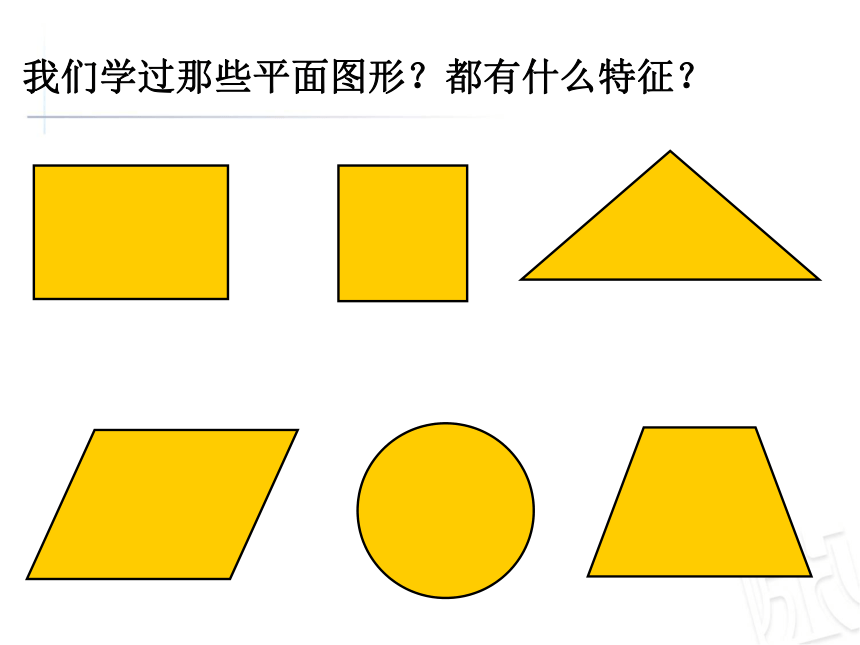
我们学过那些平面图形?都有什么特征?
本单元复习要点
面积公式及其应用
面积公式的推导
解决实际问题
发展空间观念
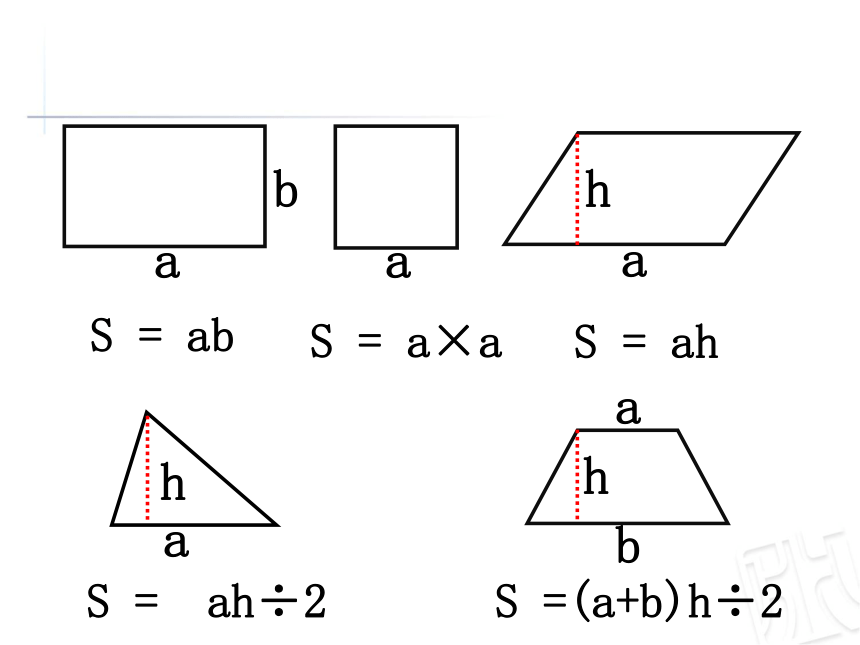
梯形的面积=
(上底+下底)×高÷2
长方形的面积=长×宽
正方形的面积=边长×边长
平行四边形的面积=底×高
三角形的面积=底×高÷2
S = a×a
S = ab
S = ah
a
a
b
a
h
S = ah÷2
S =(a+b)h÷2
a
h
a
b
h
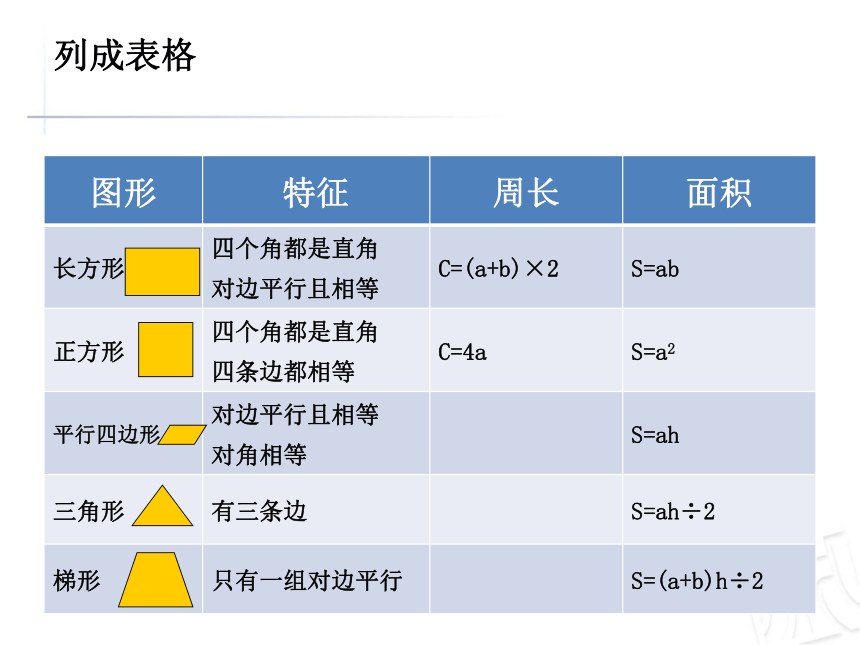
列成表格
图形 特征 周长 面积
长方形 四个角都是直角
对边平行且相等 C=(a+b)×2 S=ab
正方形 四个角都是直角
四条边都相等 C=4a S=a2
平行四边形 对边平行且相等
对角相等 S=ah
三角形 有三条边 S=ah÷2
梯形 只有一组对边平行 S=(a+b)h÷2
组合图形的面积
(1)把组合图形分割成几个简单简单图形,分别求出每个简单图形的面积,再把各部分面积加起来。
(2)把组合图形添补成一个简单图形,然后用简单图形的面积减去添补部分的面积。
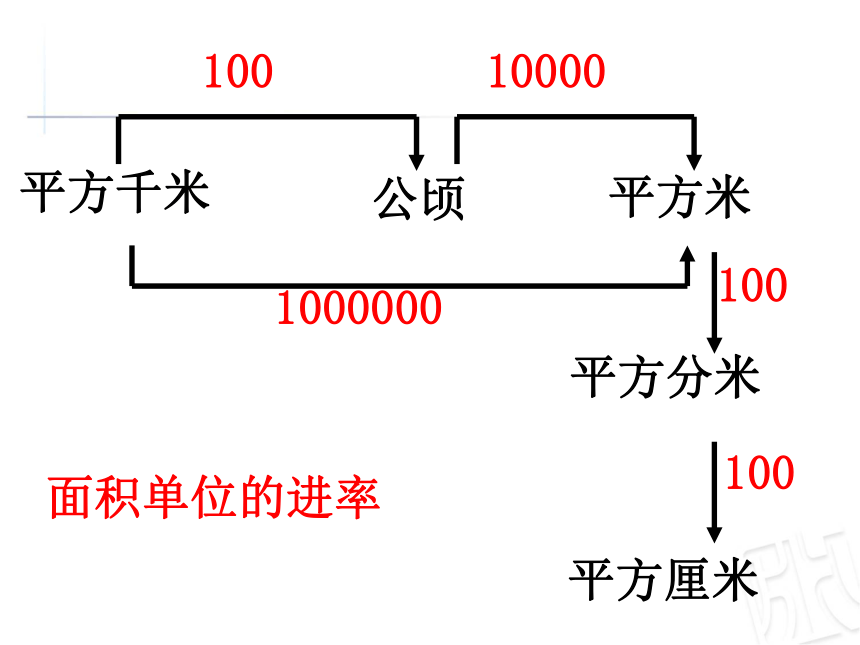
平方千米
公顷
平方米
平方分米
平方厘米
100
10000
100
100
1000000
面积单位的进率
①520公顷=( )平方千米
②0.27平方千米=( )公顷
5.2
27
③1.8公顷=( )平方千米
④1.5公顷=( )平方米
⑤1.15平方米=( )平方分米
=( )平方厘米
0.018
15000
115
11500
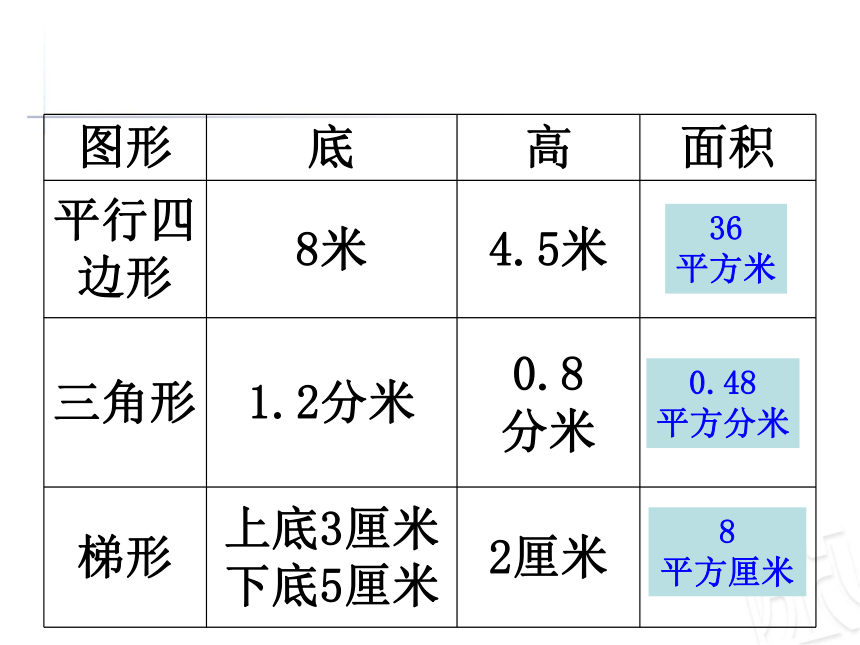
图形 底 高 面积
平行四边形 8米 4.5米 ①
三角形 1.2分米 0.8
分米 ②
梯形 上底3厘米
下底5厘米 2厘米 ③
36
平方米
0.48
平方分米
8
平方厘米
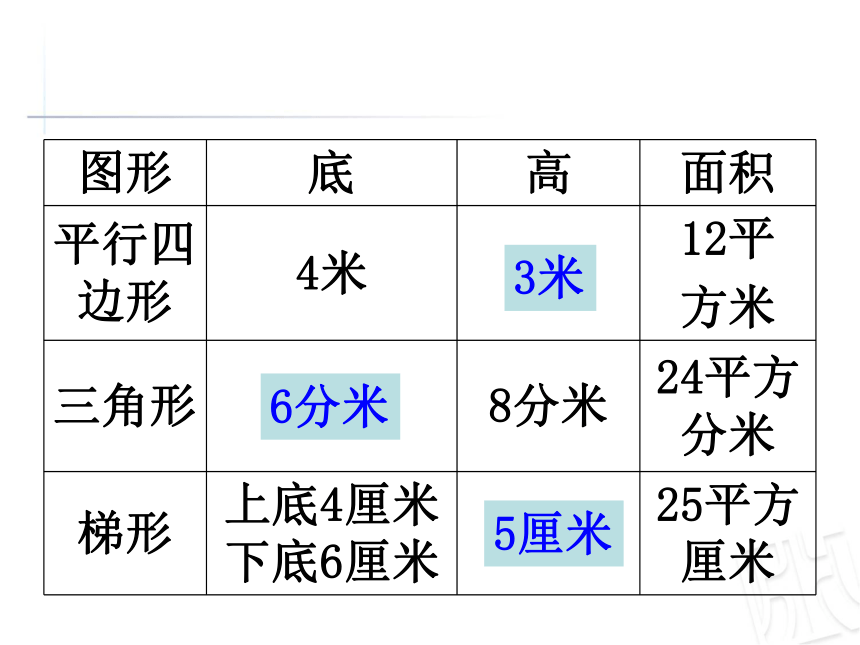
图形 底 高 面积
平行四边形 4米 ① 12平
方米
三角形 ② 8分米 24平方分米
梯形 上底4厘米
下底6厘米 ③ 25平方厘米
3米
6分米
5厘米
一个平行四边形通过( )才能拼成一个
长方形。
割补、平移
旋转、平移
割补、旋转
①
把两个完全一样的三角形重
叠放置,通过( )才能
拼成一个平行四边形。
割补、平移
旋转、平移
割补、旋转
②
把两个完全一样的梯形重
叠放置,通过( )才
能拼成一个平行四边形。
割补、平移
旋转、平移
割补、旋转
②
下图两个平行四边形面积相等。( )
判断:
√
下图三个三角形面积相等。( )
√
三角形面积是平行四边形面积的一半。( )
×
正确的说法:
如果三角形和平行四边形的底和高都分别相等,那么三角形面积是平行四边形面积的一半。
两个面积相等的梯形,形状是相同的。 ( )
3
5
4
3
5
4
∟
×
两个完全一样的梯形可以拼成一个平行四边形。
( )
3
5
4
3
5
4
√
两个三角形的高相等,它们的面积就相等。( )
×
平行四边形的底越长,它的面积就越大。
( )
底
底
×
面积相等的两个梯形一定能拼成一个平行四边形。( )
3
5
4
3
5
4
∟
×
面积相等的两个三角形,形状也一定相同。( )
∟
3
3
4
4
×
填空
一个平行四边形面积是40平方厘米,与它等底等高的三角形面积是( )平方厘米。
20
一个平行四边形的面积是16平方厘米,从这个平行四边形中剪出一个最大的三角形,这个三角形的面积是( )平方厘米。
8
选择题
两个平行四边形面积相等,它们的底和高( )。
一定相等
不一定相等
一定不相等
B
一个三角形,高不变,底扩大到原来的3倍,面积就扩大到原来的( )倍。
3
6
9
A
3×4÷2
3×5÷2
4×5÷2
5×2.4÷2
3×2.4÷2
4×2.4÷2
求直角三角形的面积
5
4
3
∟
2.4
哪些算式正确?( )
①④
1
2
3
2
原来的面积
1×2÷2=1
现在的面积
3×2÷2=3
3倍
一块麦田(如图),去年共收小麦54吨,平均每公顷收小麦多少吨?
答:平均每公顷收小麦6吨。
一个牧场的形状如图。这个牧场的面积是多少平方米?是多少公顷?
答:这个牧场的面积是40000平方米,是4公顷。
思考题
1.下图中红色部分面积和黄色部分面积相比( )。
黄色部分面积大
红色部分面积大
一样大
不能确定
2.如果一个三角形的底和一个平行四边形的底相等,面积也相等,平行四边形的高是10厘米,那么三角形的高是多少?
多边形的面积
——回顾整理
我们学过那些平面图形?都有什么特征?
本单元复习要点
面积公式及其应用
面积公式的推导
解决实际问题
发展空间观念
梯形的面积=
(上底+下底)×高÷2
长方形的面积=长×宽
正方形的面积=边长×边长
平行四边形的面积=底×高
三角形的面积=底×高÷2
S = a×a
S = ab
S = ah
a
a
b
a
h
S = ah÷2
S =(a+b)h÷2
a
h
a
b
h
列成表格
图形 特征 周长 面积
长方形 四个角都是直角
对边平行且相等 C=(a+b)×2 S=ab
正方形 四个角都是直角
四条边都相等 C=4a S=a2
平行四边形 对边平行且相等
对角相等 S=ah
三角形 有三条边 S=ah÷2
梯形 只有一组对边平行 S=(a+b)h÷2
组合图形的面积
(1)把组合图形分割成几个简单简单图形,分别求出每个简单图形的面积,再把各部分面积加起来。
(2)把组合图形添补成一个简单图形,然后用简单图形的面积减去添补部分的面积。
平方千米
公顷
平方米
平方分米
平方厘米
100
10000
100
100
1000000
面积单位的进率
①520公顷=( )平方千米
②0.27平方千米=( )公顷
5.2
27
③1.8公顷=( )平方千米
④1.5公顷=( )平方米
⑤1.15平方米=( )平方分米
=( )平方厘米
0.018
15000
115
11500
图形 底 高 面积
平行四边形 8米 4.5米 ①
三角形 1.2分米 0.8
分米 ②
梯形 上底3厘米
下底5厘米 2厘米 ③
36
平方米
0.48
平方分米
8
平方厘米
图形 底 高 面积
平行四边形 4米 ① 12平
方米
三角形 ② 8分米 24平方分米
梯形 上底4厘米
下底6厘米 ③ 25平方厘米
3米
6分米
5厘米
一个平行四边形通过( )才能拼成一个
长方形。
割补、平移
旋转、平移
割补、旋转
①
把两个完全一样的三角形重
叠放置,通过( )才能
拼成一个平行四边形。
割补、平移
旋转、平移
割补、旋转
②
把两个完全一样的梯形重
叠放置,通过( )才
能拼成一个平行四边形。
割补、平移
旋转、平移
割补、旋转
②
下图两个平行四边形面积相等。( )
判断:
√
下图三个三角形面积相等。( )
√
三角形面积是平行四边形面积的一半。( )
×
正确的说法:
如果三角形和平行四边形的底和高都分别相等,那么三角形面积是平行四边形面积的一半。
两个面积相等的梯形,形状是相同的。 ( )
3
5
4
3
5
4
∟
×
两个完全一样的梯形可以拼成一个平行四边形。
( )
3
5
4
3
5
4
√
两个三角形的高相等,它们的面积就相等。( )
×
平行四边形的底越长,它的面积就越大。
( )
底
底
×
面积相等的两个梯形一定能拼成一个平行四边形。( )
3
5
4
3
5
4
∟
×
面积相等的两个三角形,形状也一定相同。( )
∟
3
3
4
4
×
填空
一个平行四边形面积是40平方厘米,与它等底等高的三角形面积是( )平方厘米。
20
一个平行四边形的面积是16平方厘米,从这个平行四边形中剪出一个最大的三角形,这个三角形的面积是( )平方厘米。
8
选择题
两个平行四边形面积相等,它们的底和高( )。
一定相等
不一定相等
一定不相等
B
一个三角形,高不变,底扩大到原来的3倍,面积就扩大到原来的( )倍。
3
6
9
A
3×4÷2
3×5÷2
4×5÷2
5×2.4÷2
3×2.4÷2
4×2.4÷2
求直角三角形的面积
5
4
3
∟
2.4
哪些算式正确?( )
①④
1
2
3
2
原来的面积
1×2÷2=1
现在的面积
3×2÷2=3
3倍
一块麦田(如图),去年共收小麦54吨,平均每公顷收小麦多少吨?
答:平均每公顷收小麦6吨。
一个牧场的形状如图。这个牧场的面积是多少平方米?是多少公顷?
答:这个牧场的面积是40000平方米,是4公顷。
思考题
1.下图中红色部分面积和黄色部分面积相比( )。
黄色部分面积大
红色部分面积大
一样大
不能确定
2.如果一个三角形的底和一个平行四边形的底相等,面积也相等,平行四边形的高是10厘米,那么三角形的高是多少?
