人教版七年级数学下册7.1.1 有序数对 教学设计
文档属性
| 名称 | 人教版七年级数学下册7.1.1 有序数对 教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 475.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 16:53:22 | ||
图片预览

文档简介
7.1.1 有序数对
教学目标:
1.理解有序数对的应用意义,了解平面上确定点的常用方法.
2.培养学生应用数学知识的意识,激发学生的学习兴趣.
教学重难点
重点
有序数对及平面内确定点的方法.
难点
利用有序数对表示平面内的点.
教学过程:
一、创设情境,引入新课
教师出示国庆天安门阅兵方阵,学生观察,思考这么多人如何能不出错地组成方队?
(教师引入课题:有序数对)
二、探究学习
问题1:在生活中常常需要确定物体的位置,你有过这样的经历吗?
问题2:
请第2列那个同学回答问题,你能告诉我他是谁吗?
请第2列、第3排那个同学回答问题,你能告诉我他是谁吗?
问题3: 你认为确定一个位置需要几个数据?
问题4: “5列3排”如何表示?(4,5)表示的含义是什么?
教师介绍数对的含义。
这种由两个数如(2,3)组成的表示某一具体位置的,我们就称之为数对.
尝试练习:比一比:看看哪一组能最快找出以下位置的同学.
数对 (1,3) (3,1)
(2,4) (4,2)
(3,4) (4,3)
观察上面的每组数对及它们表示的位置,你能从中得出什么结论?(同桌交流)
教师介绍有序数对的含义:
用(2,3)表示第2列第3排同学的位置,我们把这种有顺序的两个数a与b组成的数对叫做有序数对,记作(a,b).
三、尝试与反馈
1.慧眼识英雄:
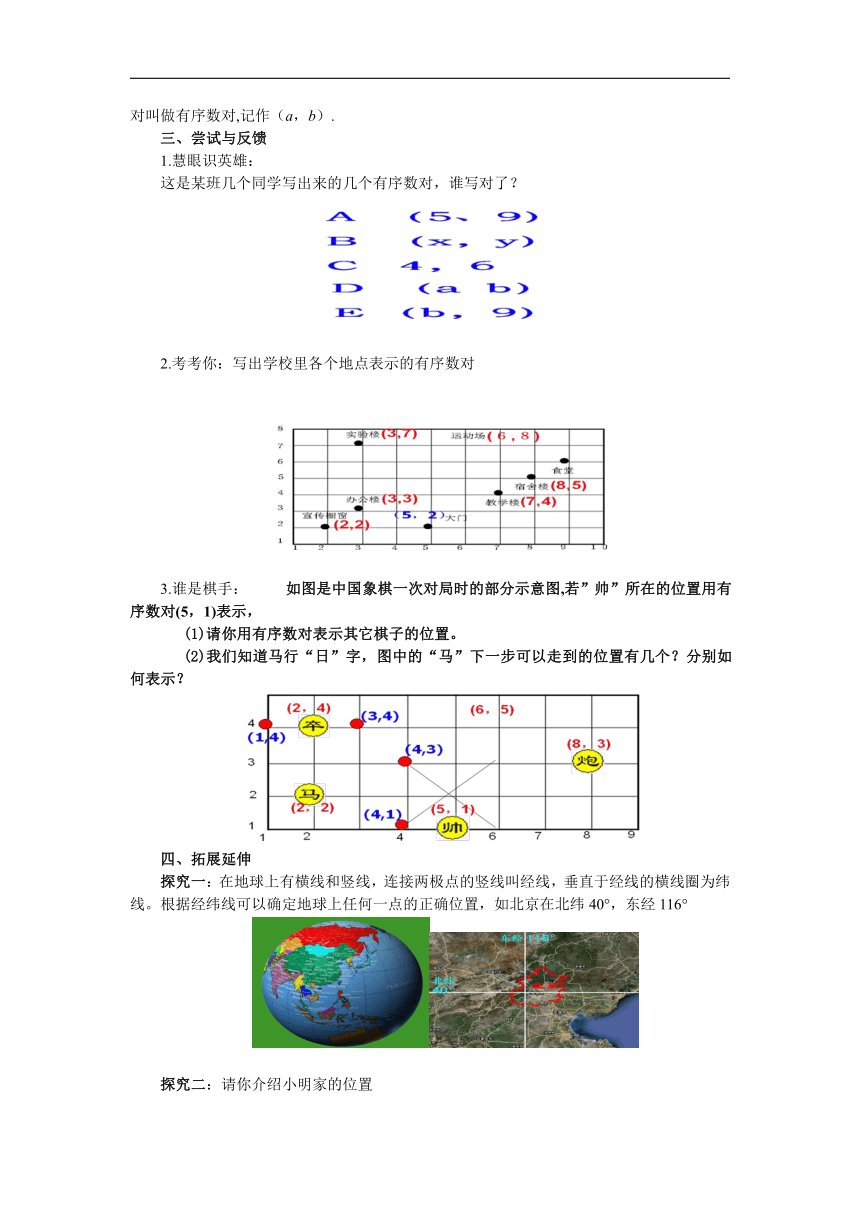
这是某班几个同学写出来的几个有序数对,谁写对了?
2.考考你:写出学校里各个地点表示的有序数对
3.谁是棋手: 如图是中国象棋一次对局时的部分示意图,若”帅”所在的位置用有序数对(5,1)表示,
(1)请你用有序数对表示其它棋子的位置。
(2)我们知道马行“日”字,图中的“马”下一步可以走到的位置有几个?分别如何表示?
四、拓展延伸
探究一:在地球上有横线和竖线,连接两极点的竖线叫经线,垂直于经线的横线圈为纬线。根据经纬线可以确定地球上任何一点的正确位置,如北京在北纬40°,东经116°
探究二:请你介绍小明家的位置
探索三:
1. 小猪如何走才能拿到苹果,请你告诉它苹果的位置?
2. 苹果在小猪的什么位置?
五、智慧闯关:
第一关:“怪兽吃豆豆”是一种计算机游戏,图中的●标志表示“怪兽”先后经过的几个位置,如果用(1,2)表示“怪兽”经过的第2个位置,那么你能用同样的方式表示出图中“怪兽”经过的其他几个位置吗?
第二关:如图是一台雷达探测相关目标得到的结果,若记图中目标A的位置为(1,90°),则其余各目标的位置分别是多少?
第三关:如图,甲地表示2街与5巷的十字路口,乙地表示5街与2巷的十字路口,如果用(2,5)表示甲地的位置,那么“(2,5)→(3,5) →(4,5) →(5,5) →(5,4) →(5,3) →(5,2)”表示从甲地到乙地的一种路线,请您用有序数对写出另1种从甲地到乙地的路线。
六、收获与困惑:
1.有什么收获与大家分享
2.有什么困惑我们帮你解答
七、课后练习:
数学书65页练习 68页第1题
教学目标:
1.理解有序数对的应用意义,了解平面上确定点的常用方法.
2.培养学生应用数学知识的意识,激发学生的学习兴趣.
教学重难点
重点
有序数对及平面内确定点的方法.
难点
利用有序数对表示平面内的点.
教学过程:
一、创设情境,引入新课
教师出示国庆天安门阅兵方阵,学生观察,思考这么多人如何能不出错地组成方队?
(教师引入课题:有序数对)
二、探究学习
问题1:在生活中常常需要确定物体的位置,你有过这样的经历吗?
问题2:
请第2列那个同学回答问题,你能告诉我他是谁吗?
请第2列、第3排那个同学回答问题,你能告诉我他是谁吗?
问题3: 你认为确定一个位置需要几个数据?
问题4: “5列3排”如何表示?(4,5)表示的含义是什么?
教师介绍数对的含义。
这种由两个数如(2,3)组成的表示某一具体位置的,我们就称之为数对.
尝试练习:比一比:看看哪一组能最快找出以下位置的同学.
数对 (1,3) (3,1)
(2,4) (4,2)
(3,4) (4,3)
观察上面的每组数对及它们表示的位置,你能从中得出什么结论?(同桌交流)
教师介绍有序数对的含义:
用(2,3)表示第2列第3排同学的位置,我们把这种有顺序的两个数a与b组成的数对叫做有序数对,记作(a,b).
三、尝试与反馈
1.慧眼识英雄:
这是某班几个同学写出来的几个有序数对,谁写对了?
2.考考你:写出学校里各个地点表示的有序数对
3.谁是棋手: 如图是中国象棋一次对局时的部分示意图,若”帅”所在的位置用有序数对(5,1)表示,
(1)请你用有序数对表示其它棋子的位置。
(2)我们知道马行“日”字,图中的“马”下一步可以走到的位置有几个?分别如何表示?
四、拓展延伸
探究一:在地球上有横线和竖线,连接两极点的竖线叫经线,垂直于经线的横线圈为纬线。根据经纬线可以确定地球上任何一点的正确位置,如北京在北纬40°,东经116°
探究二:请你介绍小明家的位置
探索三:
1. 小猪如何走才能拿到苹果,请你告诉它苹果的位置?
2. 苹果在小猪的什么位置?
五、智慧闯关:
第一关:“怪兽吃豆豆”是一种计算机游戏,图中的●标志表示“怪兽”先后经过的几个位置,如果用(1,2)表示“怪兽”经过的第2个位置,那么你能用同样的方式表示出图中“怪兽”经过的其他几个位置吗?
第二关:如图是一台雷达探测相关目标得到的结果,若记图中目标A的位置为(1,90°),则其余各目标的位置分别是多少?
第三关:如图,甲地表示2街与5巷的十字路口,乙地表示5街与2巷的十字路口,如果用(2,5)表示甲地的位置,那么“(2,5)→(3,5) →(4,5) →(5,5) →(5,4) →(5,3) →(5,2)”表示从甲地到乙地的一种路线,请您用有序数对写出另1种从甲地到乙地的路线。
六、收获与困惑:
1.有什么收获与大家分享
2.有什么困惑我们帮你解答
七、课后练习:
数学书65页练习 68页第1题
