人教版七年级数学下册5.3.1 平行线性质定理简单应用 教学设计
文档属性
| 名称 | 人教版七年级数学下册5.3.1 平行线性质定理简单应用 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 105.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 00:00:00 | ||
图片预览

文档简介
《平行线性质定理简单应用》教学设计
一、教学目标
1.理解平行线的性质与平行线的判定是相反的问题,掌握平行线的性质.
2.会用平行线的性质进行推理和计算.
3.通过平行线性质定理的推导,培养学生观察分析和进行简单的逻辑推理的能力.
4.通过学习平行线的性质与判定的联系与区别,让学生懂得事物是普遍联系又相互区别的辩证唯物主义思想.
二、学法引导
1.教师教法:采用尝试指导、引导发现法,充分发挥学生的主体作用,体现民主意识和开放意识.
2.学生学法:在教师的指导下,小组合作学习,积极思维,主动发现,认真研究.
三、重点·难点
(一)重点:平行线的性质公理及平行线性质定理的推导.
(二)难点:平行线性质与判定的区别及推导过程.
四、教学过程
(一)、复习引入
问题:平行线的判定与平行线的性质的区别是什么?
判定是已知角的关系得平行关系,性质是已知平行关系得角的关系.
两者的条件和结论刚好相反,也就是说平行线的判定与性质是互逆的.
【白板使用说明】此处使用页面特效,文字特效,引起孩子的注意力。
(二)、合作探究
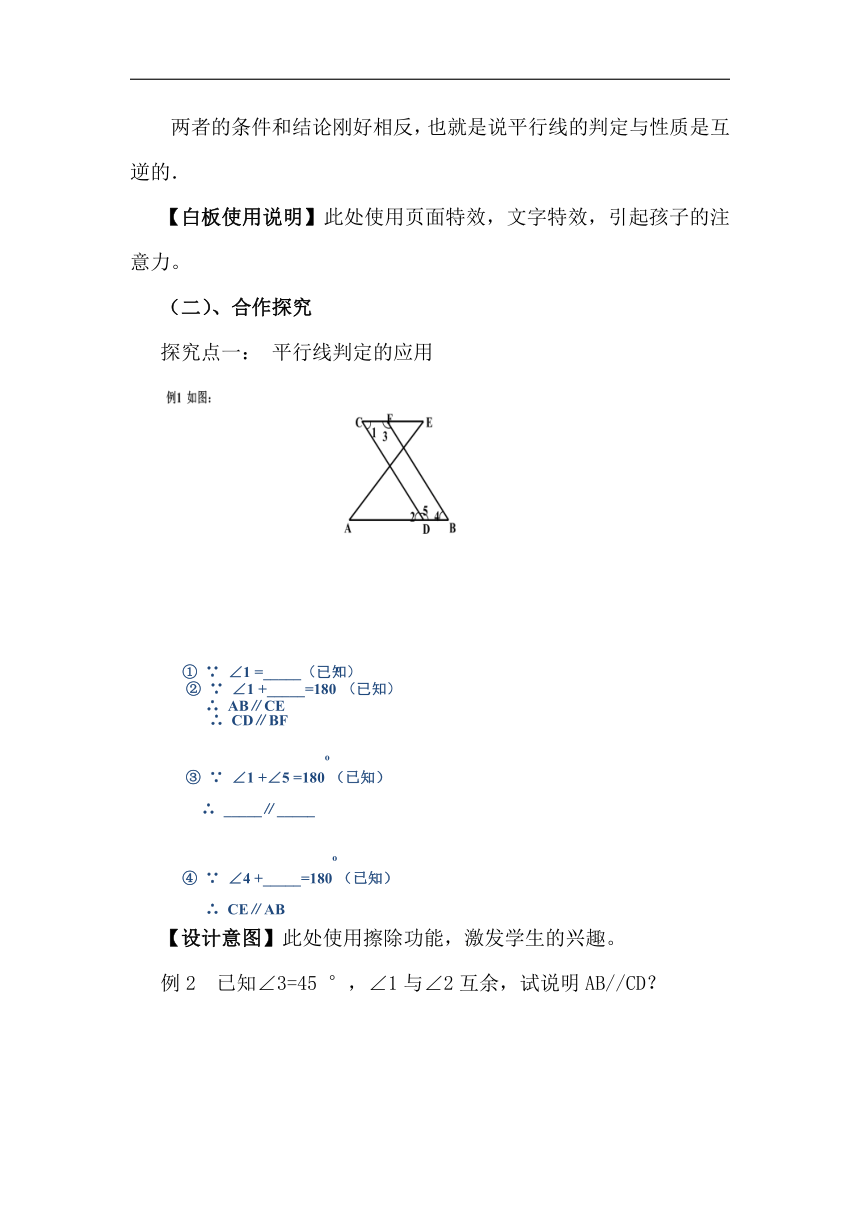
探究点一: 平行线判定的应用
【设计意图】此处使用擦除功能,激发学生的兴趣。
例2 已知∠3=45 °,∠1与∠2互余,试说明AB//CD?
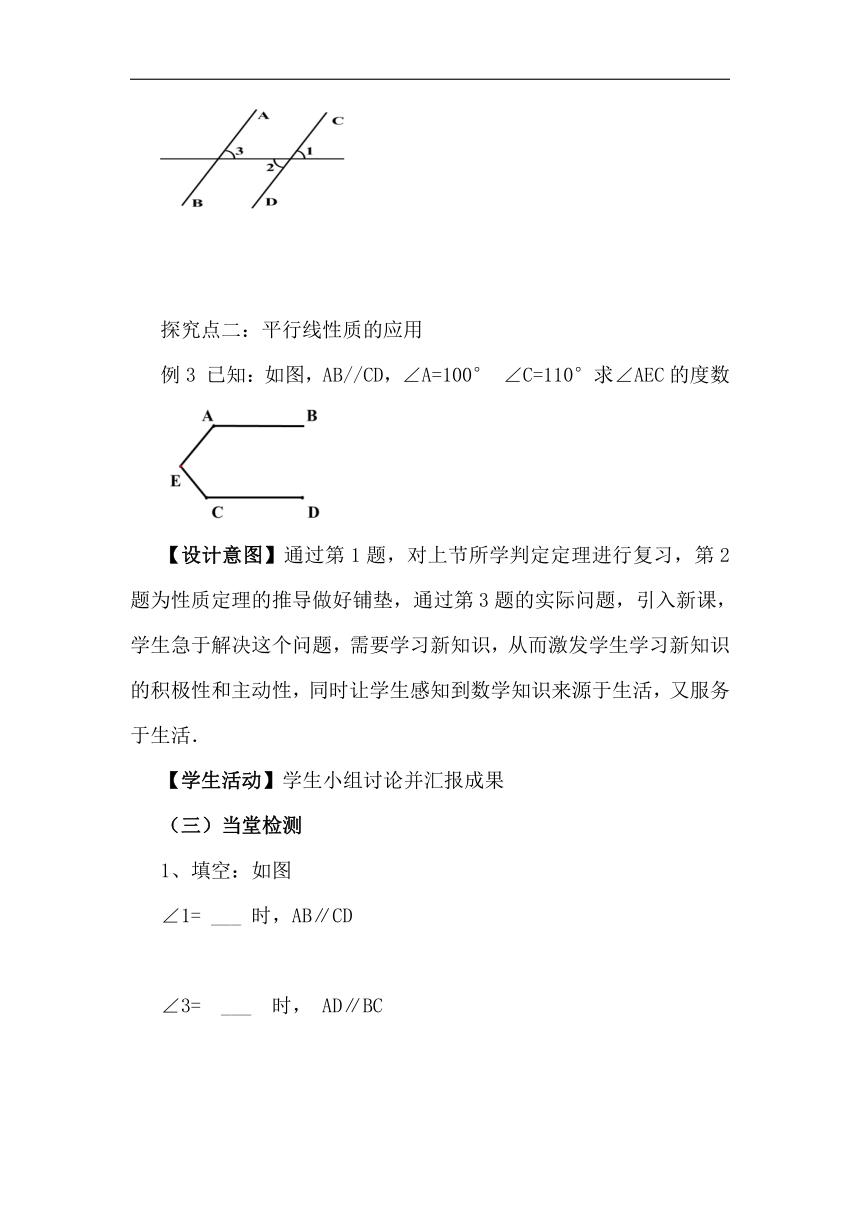
探究点二:平行线性质的应用
例3 已知:如图,AB//CD,∠A=100° ∠C=110°求∠AEC的度数
【设计意图】通过第1题,对上节所学判定定理进行复习,第2题为性质定理的推导做好铺垫,通过第3题的实际问题,引入新课,学生急于解决这个问题,需要学习新知识,从而激发学生学习新知识的积极性和主动性,同时让学生感知到数学知识来源于生活,又服务于生活.
【学生活动】学生小组讨论并汇报成果
(三)当堂检测
1、填空:如图
∠1= ___ 时,AB∥CD
∠3= ___ 时, AD∥BC
2、直线a、b与直线c相交,给出下列条件:
①∠1= ∠2 ②∠3= ∠6
③∠4+∠7=1800
④∠3+ ∠5=1800,
其中能判断a//b的是( )
A ①②③④
B ①③④
C ①③
D ④
【白板使用说明】此处使用擦除功能
3.AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3= ∠E。
【学生活动】此题让学生来讲解,并使用白板笔来标注
4、如图EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数。
【白板使用说明】第4题图形用白板中的几何图形来画,有形象感,还使用聚光灯,为了突出效果
5、已知AB∥DE,试问∠B、∠E、∠BCE有什么关系。请完成填空:
拓展提升:已知:如图,AB//CD,试解决下列问题:
(1)∠1+∠2=___ ___;
(2)∠1+∠2+∠3=___ __;
(3)∠1+∠2+∠3+∠4=_ __ __;
(4)试探究∠1+∠2+∠3+∠4+…+∠n= ___ ___ ;
学生活动:学生独立完成,把理由写成推理格式.
【设计意图】题目中的为什么,可以用语言叙述,为了培养学生的逻辑推理能力,最好用推理格式说明.对学生中出现的不同解法给予肯定,若学生未想到用邻补角求解,教师应启发诱导学生,从而培养学生的解题能力.
(四)、小结
学生活动:学生积极思考,并能够说出前面是平行线的判定,后面是平行线的性质,由角的关系得到两条直线平行的结论是平行线的判定,反过来,由已知直线平行,得到角相等或互补的结论是平行线的性质.
【设计意图】通过有形的具体实例,使学生在有充足的感性认识的基础上上升到理性认识,总结出平行线性质与判定的不同.
六、布置作业
(一)必做题
(二)选做题
七、板书设计
两直线平行
教学反思
本节内容的重点是平行线的性质及判定的综合应用,直接运用了“∵”“∴”的推理形式,为学生创设了一个学习推理的环境,逐步培养学生的逻辑推理能力.因此,这一节课有着承上启下的作用,比较重要.本节内容的难点是理解平行线的性质和判定的区别,并在推理中正确地应用.由于学生还没有学习命题的概念和命题的组成,不知道判定和性质的本质区别和联系是什么,所以在教学中,应让学生通过应用和讨论,体会到如果已知角的关系,推出两直线平行,就是平行线的判定;反之,如果两直线平行,得出角的关系,就是平行线的性质
一、教学目标
1.理解平行线的性质与平行线的判定是相反的问题,掌握平行线的性质.
2.会用平行线的性质进行推理和计算.
3.通过平行线性质定理的推导,培养学生观察分析和进行简单的逻辑推理的能力.
4.通过学习平行线的性质与判定的联系与区别,让学生懂得事物是普遍联系又相互区别的辩证唯物主义思想.
二、学法引导
1.教师教法:采用尝试指导、引导发现法,充分发挥学生的主体作用,体现民主意识和开放意识.
2.学生学法:在教师的指导下,小组合作学习,积极思维,主动发现,认真研究.
三、重点·难点
(一)重点:平行线的性质公理及平行线性质定理的推导.
(二)难点:平行线性质与判定的区别及推导过程.
四、教学过程
(一)、复习引入
问题:平行线的判定与平行线的性质的区别是什么?
判定是已知角的关系得平行关系,性质是已知平行关系得角的关系.
两者的条件和结论刚好相反,也就是说平行线的判定与性质是互逆的.
【白板使用说明】此处使用页面特效,文字特效,引起孩子的注意力。
(二)、合作探究
探究点一: 平行线判定的应用
【设计意图】此处使用擦除功能,激发学生的兴趣。
例2 已知∠3=45 °,∠1与∠2互余,试说明AB//CD?
探究点二:平行线性质的应用
例3 已知:如图,AB//CD,∠A=100° ∠C=110°求∠AEC的度数
【设计意图】通过第1题,对上节所学判定定理进行复习,第2题为性质定理的推导做好铺垫,通过第3题的实际问题,引入新课,学生急于解决这个问题,需要学习新知识,从而激发学生学习新知识的积极性和主动性,同时让学生感知到数学知识来源于生活,又服务于生活.
【学生活动】学生小组讨论并汇报成果
(三)当堂检测
1、填空:如图
∠1= ___ 时,AB∥CD
∠3= ___ 时, AD∥BC
2、直线a、b与直线c相交,给出下列条件:
①∠1= ∠2 ②∠3= ∠6
③∠4+∠7=1800
④∠3+ ∠5=1800,
其中能判断a//b的是( )
A ①②③④
B ①③④
C ①③
D ④
【白板使用说明】此处使用擦除功能
3.AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3= ∠E。
【学生活动】此题让学生来讲解,并使用白板笔来标注
4、如图EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数。
【白板使用说明】第4题图形用白板中的几何图形来画,有形象感,还使用聚光灯,为了突出效果
5、已知AB∥DE,试问∠B、∠E、∠BCE有什么关系。请完成填空:
拓展提升:已知:如图,AB//CD,试解决下列问题:
(1)∠1+∠2=___ ___;
(2)∠1+∠2+∠3=___ __;
(3)∠1+∠2+∠3+∠4=_ __ __;
(4)试探究∠1+∠2+∠3+∠4+…+∠n= ___ ___ ;
学生活动:学生独立完成,把理由写成推理格式.
【设计意图】题目中的为什么,可以用语言叙述,为了培养学生的逻辑推理能力,最好用推理格式说明.对学生中出现的不同解法给予肯定,若学生未想到用邻补角求解,教师应启发诱导学生,从而培养学生的解题能力.
(四)、小结
学生活动:学生积极思考,并能够说出前面是平行线的判定,后面是平行线的性质,由角的关系得到两条直线平行的结论是平行线的判定,反过来,由已知直线平行,得到角相等或互补的结论是平行线的性质.
【设计意图】通过有形的具体实例,使学生在有充足的感性认识的基础上上升到理性认识,总结出平行线性质与判定的不同.
六、布置作业
(一)必做题
(二)选做题
七、板书设计
两直线平行
教学反思
本节内容的重点是平行线的性质及判定的综合应用,直接运用了“∵”“∴”的推理形式,为学生创设了一个学习推理的环境,逐步培养学生的逻辑推理能力.因此,这一节课有着承上启下的作用,比较重要.本节内容的难点是理解平行线的性质和判定的区别,并在推理中正确地应用.由于学生还没有学习命题的概念和命题的组成,不知道判定和性质的本质区别和联系是什么,所以在教学中,应让学生通过应用和讨论,体会到如果已知角的关系,推出两直线平行,就是平行线的判定;反之,如果两直线平行,得出角的关系,就是平行线的性质
