【人教版】数学九年级全一册 22.2 二次函数与一元二次方程(1) 随堂练习(课件版)
文档属性
| 名称 | 【人教版】数学九年级全一册 22.2 二次函数与一元二次方程(1) 随堂练习(课件版) |

|
|
| 格式 | ppt | ||
| 文件大小 | 885.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 18:09:27 | ||
图片预览








文档简介
(共23张PPT)
第10课 二次函数与一元二次方程(1)
——抛物线与坐标轴的交点
第二十二章 二次函数
温故知新
x=-2
-6
(0,-6)
3
(3,0)
新课学习
求抛物线y=ax2+bx+c与坐标轴的交点坐标
(3,0) ,(-1,0)
(0,-3)
(-3,0),(0,0)
(0,0)
(4,0),(-1,0)
(0,-4)
(0,-3)
x1=-1,x2=2
二次函数与一元二次方程的解
判断抛物线y=ax2+bx+c与x公共点个数
A
二次函数与一元二次方程的关系总结
三级检测
(3,0),(-2,0)
(0,-6)
A
(3,0)
4
D
2 026
下页
上页
y个
X=2
1
I
I
-1
I
5
I
70
1
X
△=b2-4ac
方程ax2+bx+c=0(a≠0)
抛物线y=ax2+bx+c(a≠0)
4>0
有两个不相等的实数根
与x轴有2个交点
△=0
有两个相等的实数根
与x轴有1个交点
△<0
没有实数根
与x轴有0个交点
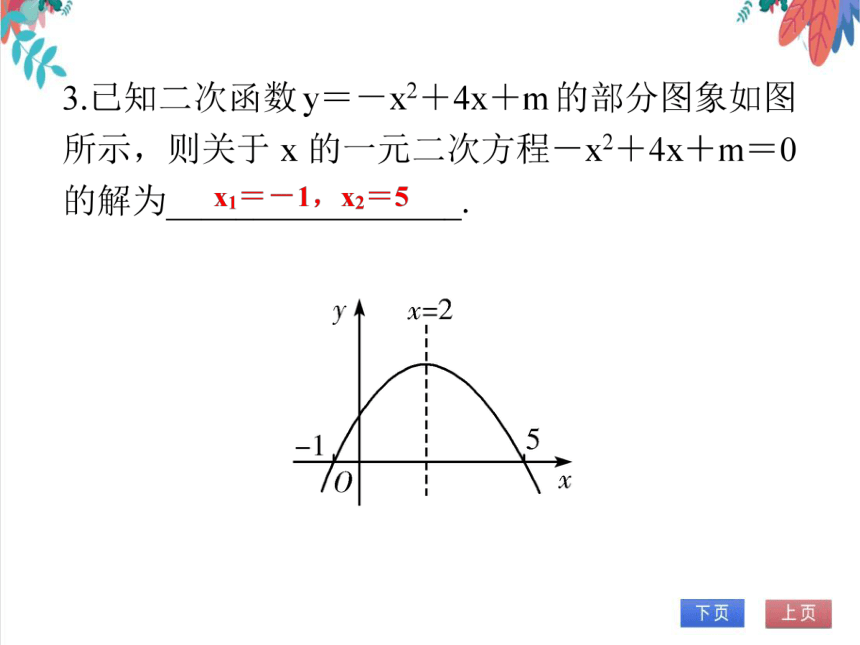
(1)若抛物线y=ax2+bx+c(a≠0)与x轴的交点为(m,0)、(n,0),则方程ax2+bx+c=0的解为x1=m,x2=n;
(2)抛物线y=ax2+bx+c(a≠0)与y轴有且只有1个交点(0,c).
第10课 二次函数与一元二次方程(1)
——抛物线与坐标轴的交点
第二十二章 二次函数
温故知新
x=-2
-6
(0,-6)
3
(3,0)
新课学习
求抛物线y=ax2+bx+c与坐标轴的交点坐标
(3,0) ,(-1,0)
(0,-3)
(-3,0),(0,0)
(0,0)
(4,0),(-1,0)
(0,-4)
(0,-3)
x1=-1,x2=2
二次函数与一元二次方程的解
判断抛物线y=ax2+bx+c与x公共点个数
A
二次函数与一元二次方程的关系总结
三级检测
(3,0),(-2,0)
(0,-6)
A
(3,0)
4
D
2 026
下页
上页
y个
X=2
1
I
I
-1
I
5
I
70
1
X
△=b2-4ac
方程ax2+bx+c=0(a≠0)
抛物线y=ax2+bx+c(a≠0)
4>0
有两个不相等的实数根
与x轴有2个交点
△=0
有两个相等的实数根
与x轴有1个交点
△<0
没有实数根
与x轴有0个交点
(1)若抛物线y=ax2+bx+c(a≠0)与x轴的交点为(m,0)、(n,0),则方程ax2+bx+c=0的解为x1=m,x2=n;
(2)抛物线y=ax2+bx+c(a≠0)与y轴有且只有1个交点(0,c).
同课章节目录
