北师大版八年级数学下册 6.4 探索多边形内角和与外角和 课件(共23张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 6.4 探索多边形内角和与外角和 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
探索多边形的内角和与外角和(1)
探索多边形的内角和与外角和(1)
生活中的平面图形
由这些图形你能抽象出什么几何图形?
三角形
矩形
四边形
六边形
八边形
多边形的定义
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
多边形的有关概念
顶点
边
内角
A
C
B
D
E
可表示为:五边形ABCDE或五边形DCBAE
对角线
上图广场中心的边缘是一个五边形,我们将共同来探求它的五个内角的和.
探
究
1
探
究
2
探
究
3
探
究
4
A
B
C
D
E
探究1
180° × 3 = 540°
O
E
A
B
C
D
探究2
180° × 5 – 360° = 540°
A
B
C
D
E
F
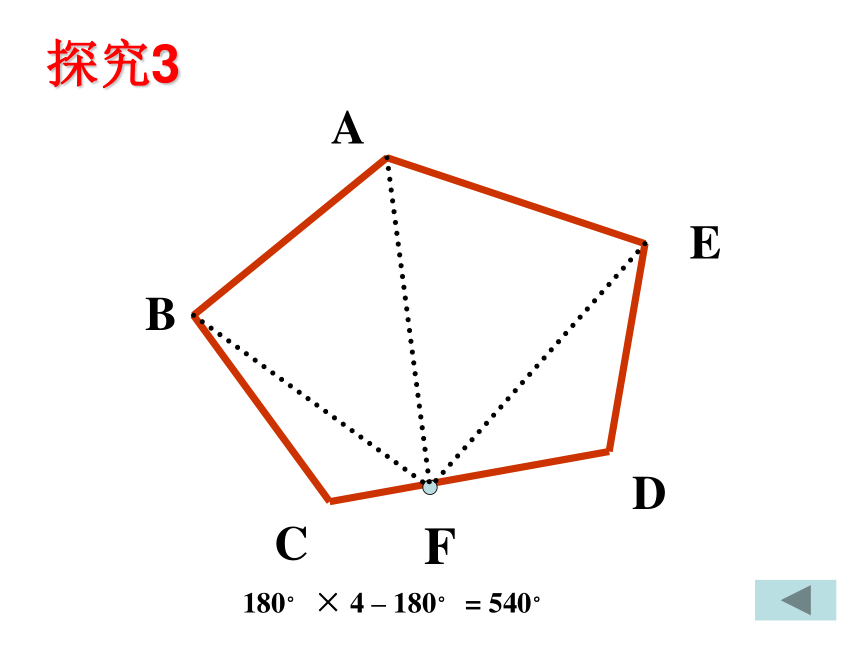
180° × 4 – 180° = 540°
探究3
探究4
A
B
C
D
E
180°+ 360° = 540°
这种探索方法你掌握了吗?请完成下表
多边形的内角和
分成的三角形个数
多边形的边数
…
360 °
180°
…
2
1
n
…
7
6
5
4
3
3
4
5
n-2
900 °
(n-2) ×180°
720 °
540 °
…
从一个顶点出发的对角线条数
…
图形示例
1
2
3
4
n-3
0
从n边形的一个顶点出发,可以引出(n-3)条对角线。
n边形被分为( n-2 )个三角形。
n 边形的内角和为:(n-2)×180°
观察图中的多边形,他们的边、角有什么特点?
在平面内,内角都相等、边也相等的多边形叫做正多边形。
议一议:
(1)一个多边形的边都相等,它的内角一定都相等吗?
(2)一个多边形的内角都相等,它的边一定都相等吗?
(3)正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的每个内角分别是多少度?
(4)正n边形的每个内角是多少度?
1.n边形的内角和等于__________,九边形的内角和等于_________________________。
2.一个多边形的内角和等于1440°,那么它是______边形。
3.正五边形的每一个内角的度数是_______。
5.一个六边形共有_____条对角线。
4.从六边形的一个顶点出发可画_____条对角线,这些对角线把六边形分成_____个三角形。
抢答题:
(n - 2) 180°
(9 - 2) 180°
= 1260°
十
108°
三
四
3
9
+3
+2
+1
=9
6.在四边形ABCD中,∠A=120度,
∠B:∠C:∠D =3:4:5,求∠B,∠C,∠D的度数。
解:设∠B,∠C,∠D的度数分别是3x , 4x , 5x 度,由 四边形的内角和等于360度可得:
120 + 3x + 4x + 5x = 360
12x = 240
x = 20
∴ 3x = 60
4x = 80
5x = 100
答:∠B,∠C,∠D的度数分别为60度,80度, 100度。
必答题:
学以致用1
小明有一个设想:
2008年奥运会在北京召开,要是能设计一个内角和是2008°的多边形花坛该多有意义啊!小明的这个想法能实现吗?
如图所示的模板,按规定AB,CD的延长线相交成80°的角, 因交点不在板上, 不便测量,质检员测得∠BAE=122°,∠DCF=155°. 如果你是质检员,如何知道模板是否合格 为什么
学以致用2
这节课你学到了什么?
知识小结:
1.什么是多边形?
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
2.n边形的内角和是多少?
n边形的内角和等于(n - 2) 180°
3.过n边形的某一个顶点的所有对角线有几条?
被分成几个三角形?
有(n - 3) 条。
被分成(n - 2) 个三角形。
在探求过程中我们使用了观察、归纳的数学方法,并且运用了类比、转化等数学思想。
作业
习题4.10 1,2,3
一个多边形去掉一个内角后形成的多边形内角和为1800度,你能求出原多边形的边数吗?
探索多边形的内角和与外角和(1)
探索多边形的内角和与外角和(1)
生活中的平面图形
由这些图形你能抽象出什么几何图形?
三角形
矩形
四边形
六边形
八边形
多边形的定义
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
多边形的有关概念
顶点
边
内角
A
C
B
D
E
可表示为:五边形ABCDE或五边形DCBAE
对角线
上图广场中心的边缘是一个五边形,我们将共同来探求它的五个内角的和.
探
究
1
探
究
2
探
究
3
探
究
4
A
B
C
D
E
探究1
180° × 3 = 540°
O
E
A
B
C
D
探究2
180° × 5 – 360° = 540°
A
B
C
D
E
F
180° × 4 – 180° = 540°
探究3
探究4
A
B
C
D
E
180°+ 360° = 540°
这种探索方法你掌握了吗?请完成下表
多边形的内角和
分成的三角形个数
多边形的边数
…
360 °
180°
…
2
1
n
…
7
6
5
4
3
3
4
5
n-2
900 °
(n-2) ×180°
720 °
540 °
…
从一个顶点出发的对角线条数
…
图形示例
1
2
3
4
n-3
0
从n边形的一个顶点出发,可以引出(n-3)条对角线。
n边形被分为( n-2 )个三角形。
n 边形的内角和为:(n-2)×180°
观察图中的多边形,他们的边、角有什么特点?
在平面内,内角都相等、边也相等的多边形叫做正多边形。
议一议:
(1)一个多边形的边都相等,它的内角一定都相等吗?
(2)一个多边形的内角都相等,它的边一定都相等吗?
(3)正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的每个内角分别是多少度?
(4)正n边形的每个内角是多少度?
1.n边形的内角和等于__________,九边形的内角和等于_________________________。
2.一个多边形的内角和等于1440°,那么它是______边形。
3.正五边形的每一个内角的度数是_______。
5.一个六边形共有_____条对角线。
4.从六边形的一个顶点出发可画_____条对角线,这些对角线把六边形分成_____个三角形。
抢答题:
(n - 2) 180°
(9 - 2) 180°
= 1260°
十
108°
三
四
3
9
+3
+2
+1
=9
6.在四边形ABCD中,∠A=120度,
∠B:∠C:∠D =3:4:5,求∠B,∠C,∠D的度数。
解:设∠B,∠C,∠D的度数分别是3x , 4x , 5x 度,由 四边形的内角和等于360度可得:
120 + 3x + 4x + 5x = 360
12x = 240
x = 20
∴ 3x = 60
4x = 80
5x = 100
答:∠B,∠C,∠D的度数分别为60度,80度, 100度。
必答题:
学以致用1
小明有一个设想:
2008年奥运会在北京召开,要是能设计一个内角和是2008°的多边形花坛该多有意义啊!小明的这个想法能实现吗?
如图所示的模板,按规定AB,CD的延长线相交成80°的角, 因交点不在板上, 不便测量,质检员测得∠BAE=122°,∠DCF=155°. 如果你是质检员,如何知道模板是否合格 为什么
学以致用2
这节课你学到了什么?
知识小结:
1.什么是多边形?
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
2.n边形的内角和是多少?
n边形的内角和等于(n - 2) 180°
3.过n边形的某一个顶点的所有对角线有几条?
被分成几个三角形?
有(n - 3) 条。
被分成(n - 2) 个三角形。
在探求过程中我们使用了观察、归纳的数学方法,并且运用了类比、转化等数学思想。
作业
习题4.10 1,2,3
一个多边形去掉一个内角后形成的多边形内角和为1800度,你能求出原多边形的边数吗?
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
