27.2.3相似三角形的周长与面积
文档属性
| 名称 | 27.2.3相似三角形的周长与面积 |  | |
| 格式 | zip | ||
| 文件大小 | 400.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-03 20:05:33 | ||
图片预览




文档简介
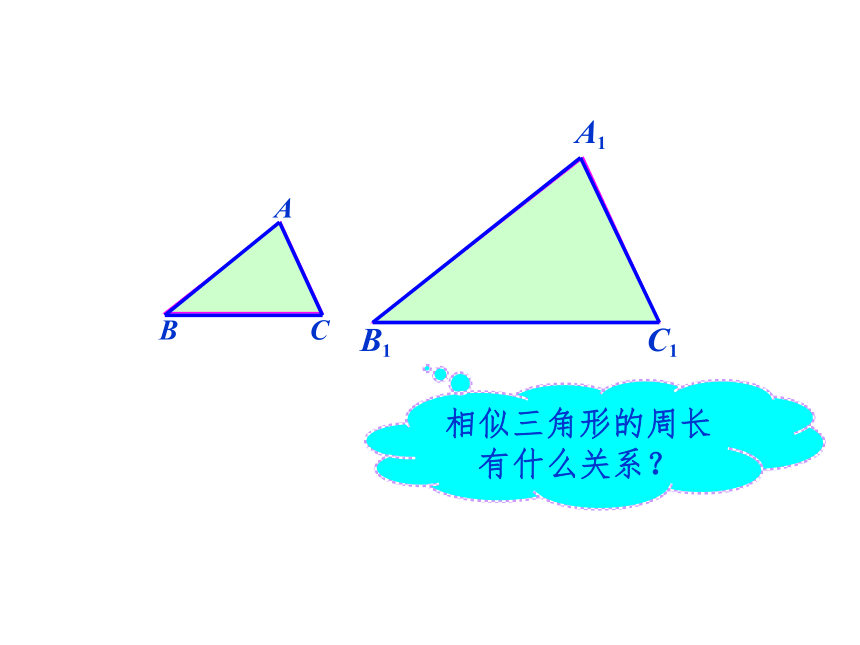
课件38张PPT。回顾旧知相似三角形有哪些性质?(1)相似三角形对应角相等。
(2)相似三角形对应边成比例。
(3)相似三角形对应高的比等于相似比。
(4)相似三角形对应中线的比等于相似比。
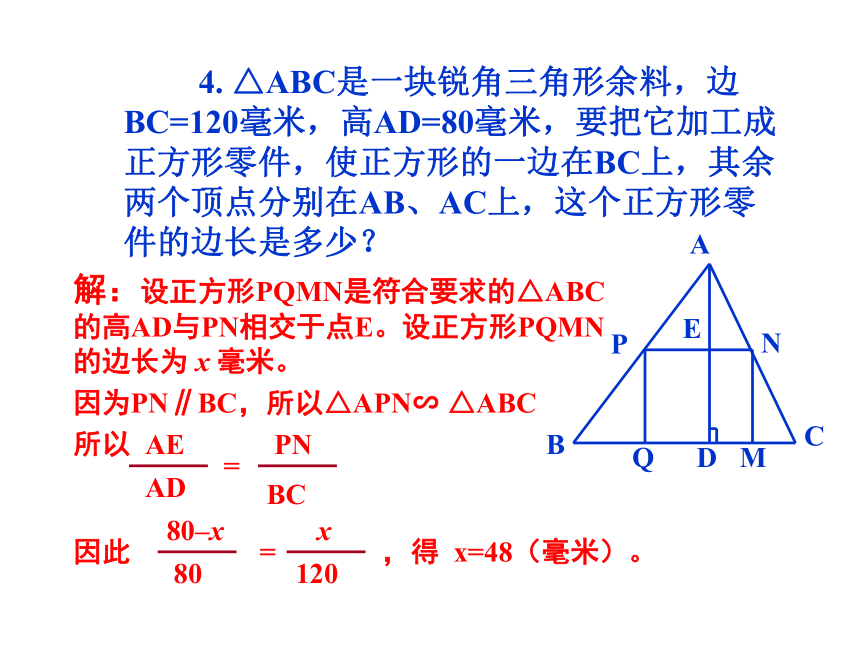
(5)相似三角形对应角平分线的比等于相似比。相似三角形的性质k 4. △ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为 x 毫米。
因为PN∥BC,所以△APN∽ △ABC
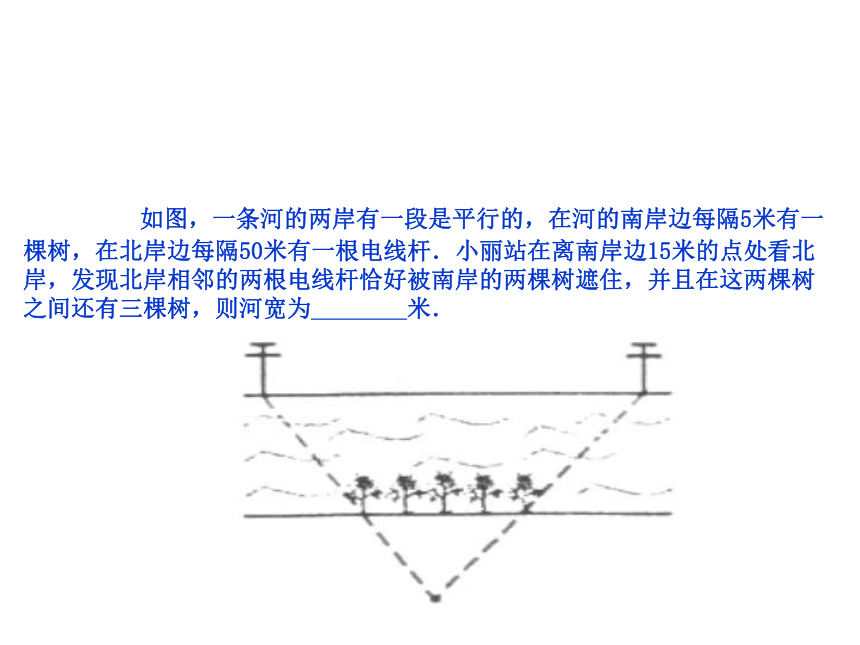
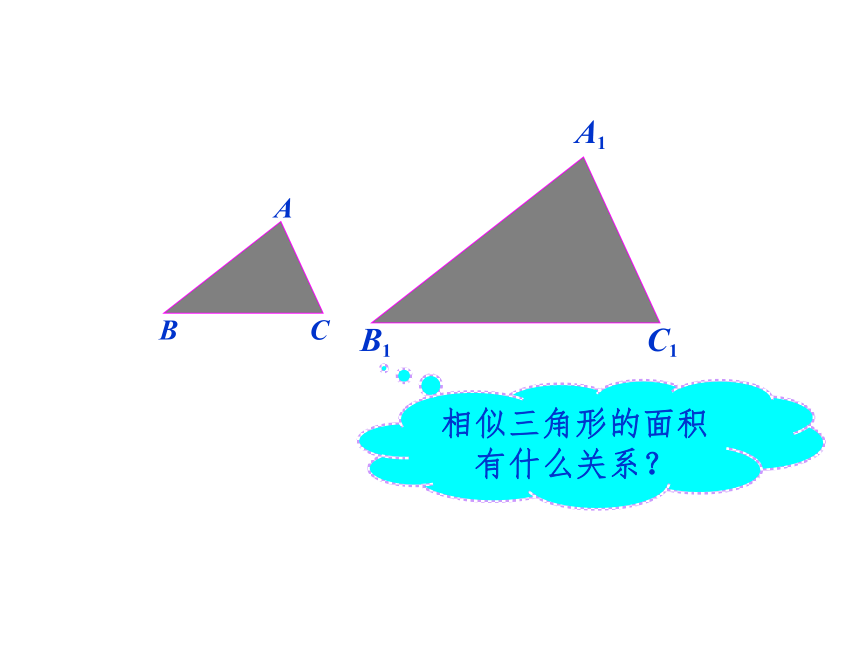
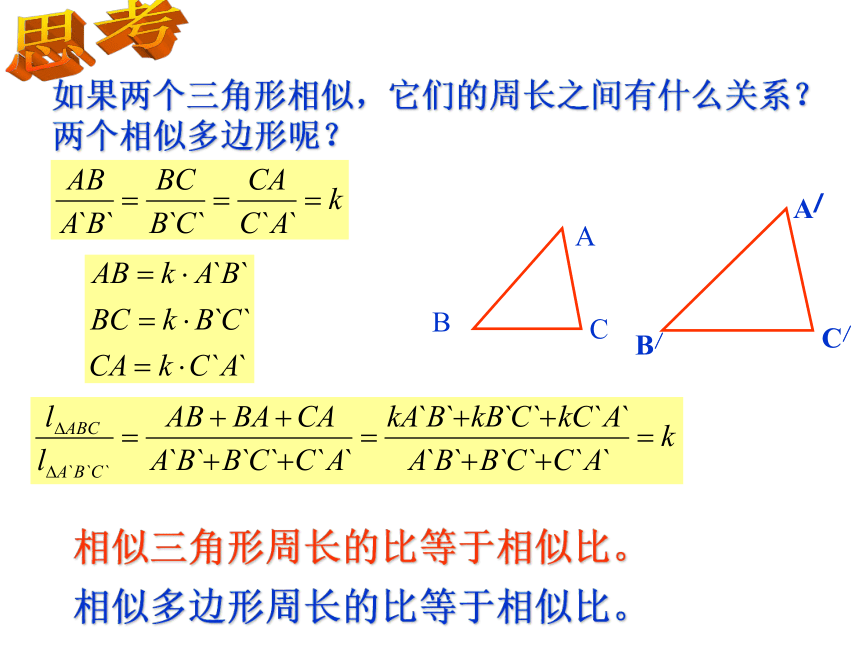
所以 如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的点处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 米.相似三角形的周长有什么关系?相似三角形的面积有什么关系?思考如果两个三角形相似,它们的周长之间有什么关系?
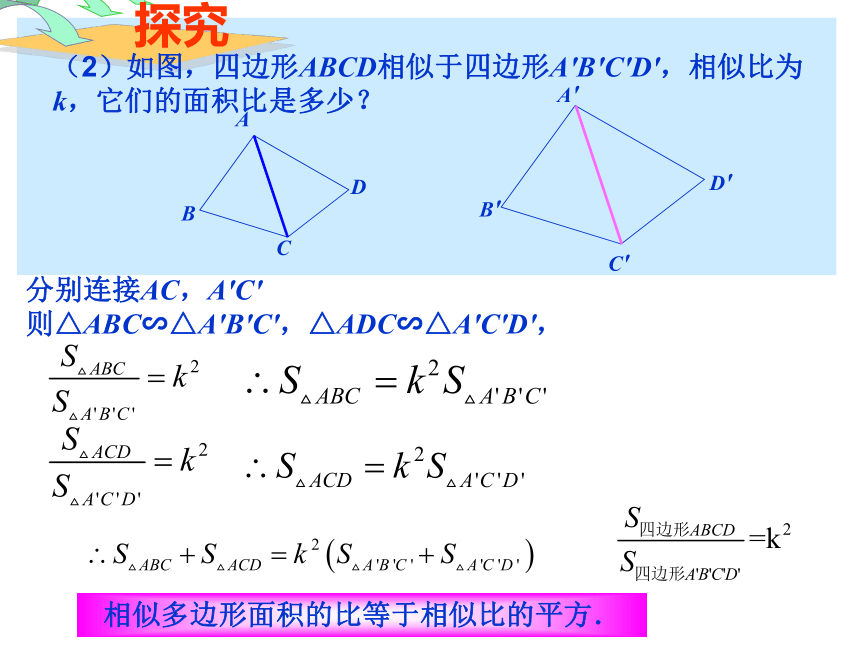
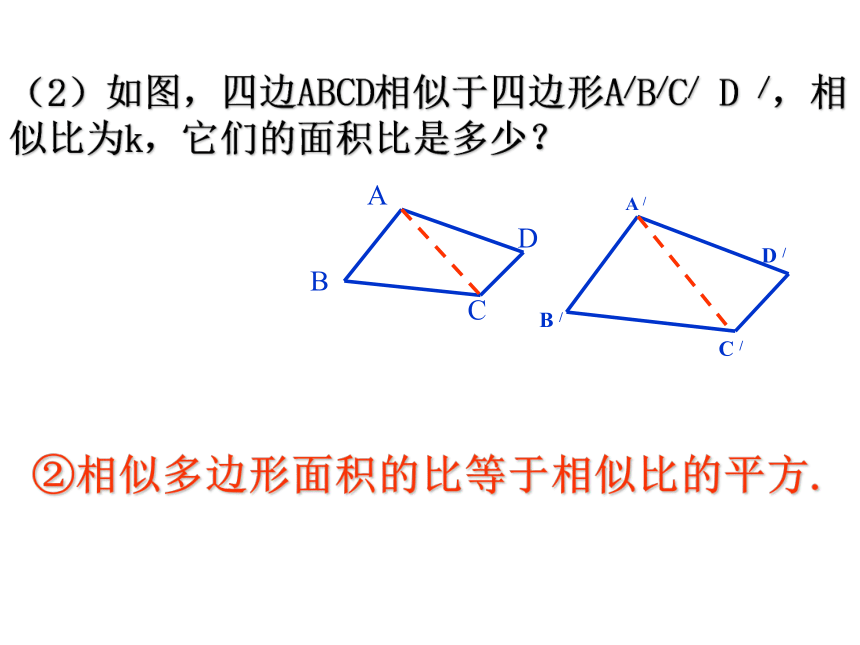
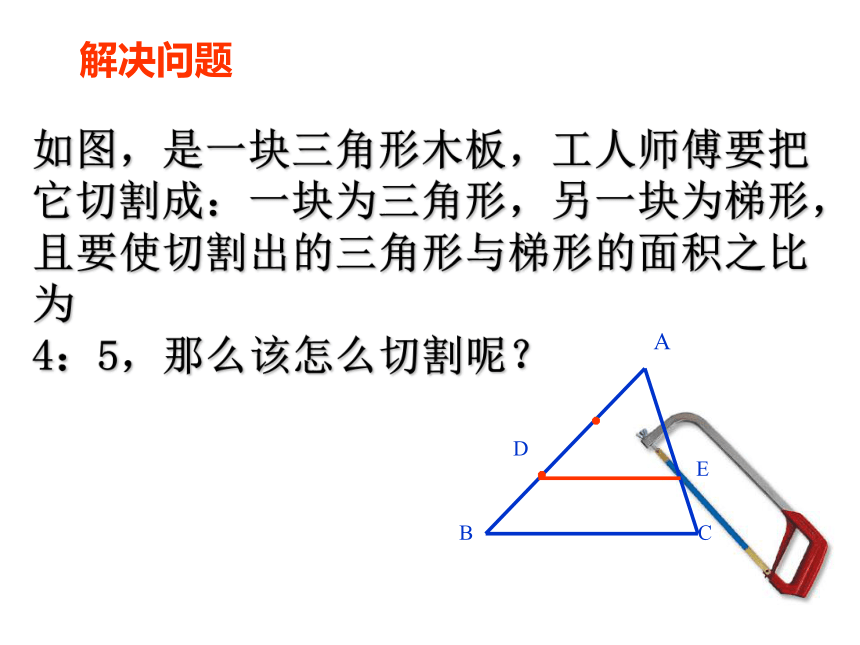
两个相似多边形呢?相似三角形周长的比等于相似比。相似多边形周长的比等于相似比。S△ABC =面积:S△A1B1C1 =∵∴∴相似三角形面积的比等于相似比的平方。DD127.2.1中,我们知道对应高之比等于相似比。=== k2(2)如图,四边形ABCD相似于四边形A'B'C'D',相似比为k,它们的面积比是多少?ABCDA'B'C'D'则△ABC∽△A'B'C',△ADC∽△A'C'D',相似多边形面积的比等于相似比的平方.分别连接AC,A'C'(2)如图,四边ABCD相似于四边形A/B/C/ D /,相似比为k,它们的面积比是多少?②相似多边形面积的比等于相似比的平方.如图,是一块三角形木板,工人师傅要把它切割成:一块为三角形,另一块为梯形,且要使切割出的三角形与梯形的面积之比为
4:5,那么该怎么切割呢?DE解决问题相似三角形的性质对应角相等对应边成比例对应高的比,对应中线的比、对应角平分线的比都等于相似比.相似比等于对应边的比周长的比等于相似比面积的比等于相似比的平方运用新知练习:
(1)已知ΔABC与ΔA/B/C/ 的相似比为2:3,
则周长比为 ,对应边上中线之比 ,
面积之比为 。
(2)已知ΔABC∽ΔA/B/C/,且面积之比为9:4,
则周长之比为 ,相似比 ,对应边上的
高线之比 。 2:34:93:23: 23:22:3如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,面积是48,求△DEF的周长和面积.解:在△ABC和△DEF中,∵ AB=2DE,AC=2DF∴又 ∠D=∠A∴ △DEF∽△ABC,相似比为ABCDEF 例题分析1、判断题:(1)如果把一个三角形各边同时扩大为原来的5倍,那么它的周长也扩大为原来的5倍。(√)(2)如果把一个三角形的面积扩大为原来的9倍,那么它的三边也扩大为原来的9倍。(×)基础练习2.如图,△ABC∽△A'B'C',他们的周长分别为60cm和72cm,且AB=15cm,B'C'=24cm,求BC、AC、A'B'、A'C'的长.3.把一个三角形变成和它相似的三角形,
(1)如果面积扩大为原来的100倍,那么边长扩大为原来的________倍。
(2)如图在等边三角形ABC中,点D、
E分别在AB、AC边上,且DE∥BC,
如果BC=8cm,AD:AB=1:4,那么△ADE
的周长等于_______cm。
4.两个相似三角形的一对对应边分别是35厘米和14 厘米,
(1)它们的周长差60厘米,这两个三角形的周长分别是
——————。
(2)它们的面积之和是232平方厘米,这两个三角形的面积分别是_____________。5. 蛋糕店制作两种圆形蛋糕,一种半径是15cm,一种半径是30cm,如果半径是15cm的蛋糕够2个人吃,半径是30cm的蛋糕够多少人吃?(假设两种蛋糕高度相同)解:两块蛋糕是相似的相似比是1:2面积的比为设半径是30cm的蛋糕够x人吃1:4=2:xx = 8答:半径是30cm的蛋糕够8个人吃.6. 在一张复印出来的纸上,一个多边形的一条边由原图中的2cm变成了6cm,这次复印的放缩比例是多少?这个多边形的面积发生了怎样的变化?解:放缩比例为面积发生了7.如图,这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少?8.某施工队在道路拓宽施工时遇到这样一个问题,马路旁边
原有一个面积为100平方米,周长为80米的三角形绿化地,
由于马路拓宽绿地被削去了一个角,变成了一个梯形,原
绿化地一边AB的长由原来的30米缩短成18米.现在的问题是:
被削去的部分面积有多大?它的周长是多少?5、如图,在△ABC中,D是AB的中点,
DE∥ BC,则:(1)S △ADE : S △ABC =(2)S △ADE: S 梯形DBCE =1:41:3* 5、如图,在△ABC中,D、F是AB的三 等分点, DE∥FG ∥ BC,则:1:4:9(1)S △ADE: S △AFG : S △ABC =(2)S △ADE: S 梯形DFGE: S 梯形FBCG =1:3:56、如图,△ABC,DE//BC,且△ADE的面积
等于梯形BCED的面积,则△ADE与△ABC的
相似比是_______
*6、如图,△ABC,DE// FG// BC ,且△ADE的面积,梯形FBCG的面积,梯形DFGE的面积均相等,则△ADE与△ABC的
相似比是_______;
△AFG与△ABC的
相似比是_______.7、△ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,求△ABC的面积。8、如图,平行四边形ABCD中,AE:EB=1:2,求△AEF与△CDF周长的比。如果S△AEF=6 cm2,求S△CDF? 课堂小结(1)相似三角形对应的 比等于相似比.相似三角形(多边形)的性质:(3)相似 面积的比等于相似比的平方.多边形多边形(2)相似 周长的比等于相似比.三角形三角形高线角平分线中线基本图形:1.等分边长:2.等分面积 课后拓展1、如图,在△ABC中,点D、E分别是AB、AC的中点。
(3)若S△DOE=1cm2,求S△OBC ,S△OEC 和S△ABC.(1)找出图中的各对相似三角形;(2)各对相似三角形的相似比
分别是多少?面积的比呢? 2.如图, ABCD中,E为AD的中点,若
S ABCD=1,则图中阴影部分的面积为( )
A、 B、 C、 D、C3.如图,S□ABCD=2008cm2,点E是平行四边形ABCD
的边AB的延长线上一点,且 ,那么
S△BEF = . 5、如图,矩形FGHN内接于△ABC,FG在BC上,NH分别在AB、AC上,且AD⊥BC于D,交NH于E,AD=8cm,BC=24cm,
(1) △ABC∽ △ANH成立吗?试说明理由;
(2)设矩形的一边长NF=x,求矩形 FGHN 的面积y与x的关系式。(3)你能求出矩形FGHN
的面积y的最大值吗?
4、 如图,△ABC是一块锐角三角形余料,
边BC=120毫米,高AD=80毫米,要把它加
工成正方形零件,使正方形的一边在BC上,
其余两个顶点分别在AB、AC上,这个正方
形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
∵PN∥BC ∴△APN∽ △ABC
∴
(2)相似三角形对应边成比例。
(3)相似三角形对应高的比等于相似比。
(4)相似三角形对应中线的比等于相似比。
(5)相似三角形对应角平分线的比等于相似比。相似三角形的性质k 4. △ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为 x 毫米。
因为PN∥BC,所以△APN∽ △ABC
所以 如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的点处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 米.相似三角形的周长有什么关系?相似三角形的面积有什么关系?思考如果两个三角形相似,它们的周长之间有什么关系?
两个相似多边形呢?相似三角形周长的比等于相似比。相似多边形周长的比等于相似比。S△ABC =面积:S△A1B1C1 =∵∴∴相似三角形面积的比等于相似比的平方。DD127.2.1中,我们知道对应高之比等于相似比。=== k2(2)如图,四边形ABCD相似于四边形A'B'C'D',相似比为k,它们的面积比是多少?ABCDA'B'C'D'则△ABC∽△A'B'C',△ADC∽△A'C'D',相似多边形面积的比等于相似比的平方.分别连接AC,A'C'(2)如图,四边ABCD相似于四边形A/B/C/ D /,相似比为k,它们的面积比是多少?②相似多边形面积的比等于相似比的平方.如图,是一块三角形木板,工人师傅要把它切割成:一块为三角形,另一块为梯形,且要使切割出的三角形与梯形的面积之比为
4:5,那么该怎么切割呢?DE解决问题相似三角形的性质对应角相等对应边成比例对应高的比,对应中线的比、对应角平分线的比都等于相似比.相似比等于对应边的比周长的比等于相似比面积的比等于相似比的平方运用新知练习:
(1)已知ΔABC与ΔA/B/C/ 的相似比为2:3,
则周长比为 ,对应边上中线之比 ,
面积之比为 。
(2)已知ΔABC∽ΔA/B/C/,且面积之比为9:4,
则周长之比为 ,相似比 ,对应边上的
高线之比 。 2:34:93:23: 23:22:3如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,面积是48,求△DEF的周长和面积.解:在△ABC和△DEF中,∵ AB=2DE,AC=2DF∴又 ∠D=∠A∴ △DEF∽△ABC,相似比为ABCDEF 例题分析1、判断题:(1)如果把一个三角形各边同时扩大为原来的5倍,那么它的周长也扩大为原来的5倍。(√)(2)如果把一个三角形的面积扩大为原来的9倍,那么它的三边也扩大为原来的9倍。(×)基础练习2.如图,△ABC∽△A'B'C',他们的周长分别为60cm和72cm,且AB=15cm,B'C'=24cm,求BC、AC、A'B'、A'C'的长.3.把一个三角形变成和它相似的三角形,
(1)如果面积扩大为原来的100倍,那么边长扩大为原来的________倍。
(2)如图在等边三角形ABC中,点D、
E分别在AB、AC边上,且DE∥BC,
如果BC=8cm,AD:AB=1:4,那么△ADE
的周长等于_______cm。
4.两个相似三角形的一对对应边分别是35厘米和14 厘米,
(1)它们的周长差60厘米,这两个三角形的周长分别是
——————。
(2)它们的面积之和是232平方厘米,这两个三角形的面积分别是_____________。5. 蛋糕店制作两种圆形蛋糕,一种半径是15cm,一种半径是30cm,如果半径是15cm的蛋糕够2个人吃,半径是30cm的蛋糕够多少人吃?(假设两种蛋糕高度相同)解:两块蛋糕是相似的相似比是1:2面积的比为设半径是30cm的蛋糕够x人吃1:4=2:xx = 8答:半径是30cm的蛋糕够8个人吃.6. 在一张复印出来的纸上,一个多边形的一条边由原图中的2cm变成了6cm,这次复印的放缩比例是多少?这个多边形的面积发生了怎样的变化?解:放缩比例为面积发生了7.如图,这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少?8.某施工队在道路拓宽施工时遇到这样一个问题,马路旁边
原有一个面积为100平方米,周长为80米的三角形绿化地,
由于马路拓宽绿地被削去了一个角,变成了一个梯形,原
绿化地一边AB的长由原来的30米缩短成18米.现在的问题是:
被削去的部分面积有多大?它的周长是多少?5、如图,在△ABC中,D是AB的中点,
DE∥ BC,则:(1)S △ADE : S △ABC =(2)S △ADE: S 梯形DBCE =1:41:3* 5、如图,在△ABC中,D、F是AB的三 等分点, DE∥FG ∥ BC,则:1:4:9(1)S △ADE: S △AFG : S △ABC =(2)S △ADE: S 梯形DFGE: S 梯形FBCG =1:3:56、如图,△ABC,DE//BC,且△ADE的面积
等于梯形BCED的面积,则△ADE与△ABC的
相似比是_______
*6、如图,△ABC,DE// FG// BC ,且△ADE的面积,梯形FBCG的面积,梯形DFGE的面积均相等,则△ADE与△ABC的
相似比是_______;
△AFG与△ABC的
相似比是_______.7、△ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,求△ABC的面积。8、如图,平行四边形ABCD中,AE:EB=1:2,求△AEF与△CDF周长的比。如果S△AEF=6 cm2,求S△CDF? 课堂小结(1)相似三角形对应的 比等于相似比.相似三角形(多边形)的性质:(3)相似 面积的比等于相似比的平方.多边形多边形(2)相似 周长的比等于相似比.三角形三角形高线角平分线中线基本图形:1.等分边长:2.等分面积 课后拓展1、如图,在△ABC中,点D、E分别是AB、AC的中点。
(3)若S△DOE=1cm2,求S△OBC ,S△OEC 和S△ABC.(1)找出图中的各对相似三角形;(2)各对相似三角形的相似比
分别是多少?面积的比呢? 2.如图, ABCD中,E为AD的中点,若
S ABCD=1,则图中阴影部分的面积为( )
A、 B、 C、 D、C3.如图,S□ABCD=2008cm2,点E是平行四边形ABCD
的边AB的延长线上一点,且 ,那么
S△BEF = . 5、如图,矩形FGHN内接于△ABC,FG在BC上,NH分别在AB、AC上,且AD⊥BC于D,交NH于E,AD=8cm,BC=24cm,
(1) △ABC∽ △ANH成立吗?试说明理由;
(2)设矩形的一边长NF=x,求矩形 FGHN 的面积y与x的关系式。(3)你能求出矩形FGHN
的面积y的最大值吗?
4、 如图,△ABC是一块锐角三角形余料,
边BC=120毫米,高AD=80毫米,要把它加
工成正方形零件,使正方形的一边在BC上,
其余两个顶点分别在AB、AC上,这个正方
形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
∵PN∥BC ∴△APN∽ △ABC
∴
