等腰三角形
图片预览


文档简介
课件28张PPT。 等腰三角形目录
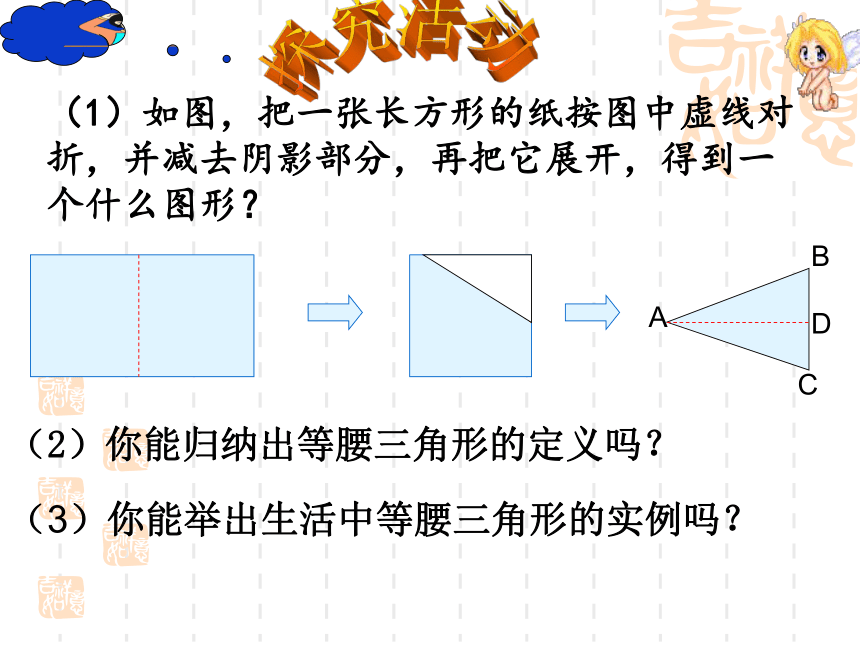
探究活动(1)如图,把一张长方形的纸按图中虚线对折,并减去阴影部分,再把它展开,得到一个什么图形?
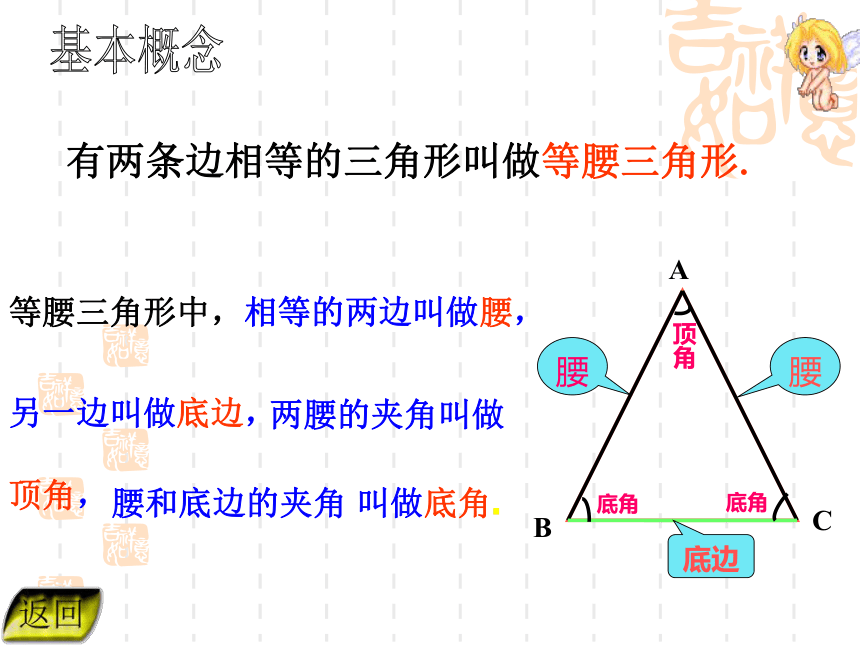
(2)你能归纳出等腰三角形的定义吗? (3)你能举出生活中等腰三角形的实例吗? 有两条边相等的三角形叫做等腰三角形. 等腰三角形中,相等的两边叫做腰,
另一边叫做底边, 两腰的夹角叫做
顶角, 腰和底边的夹角 叫做底角.底边基本概念
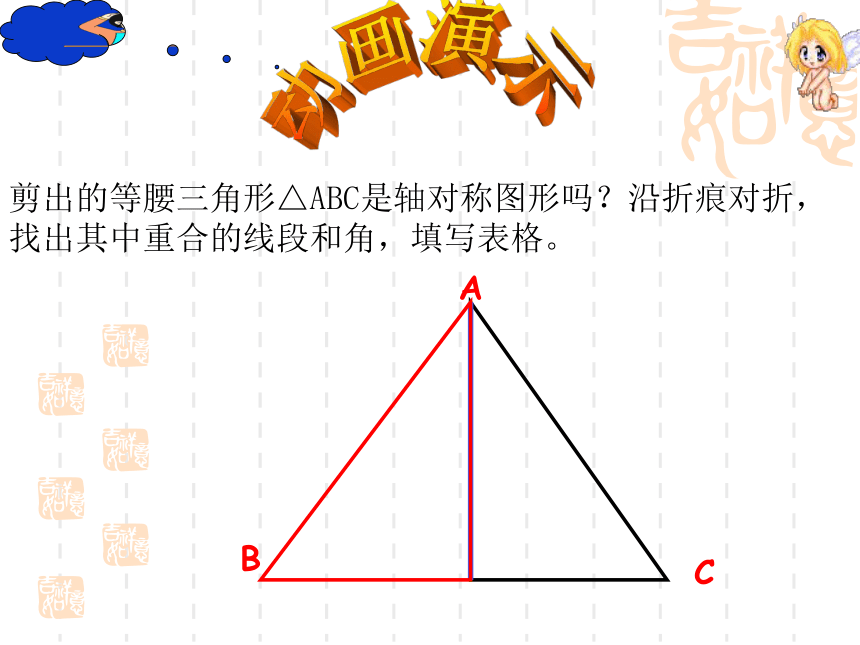
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
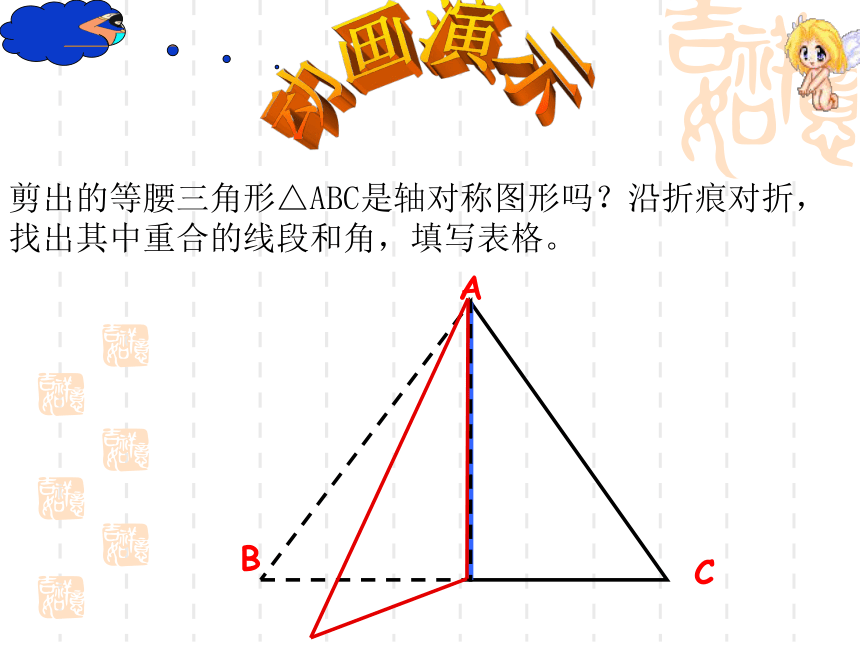
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示AC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。底角 BD=CD
指AD是底边上中线 AB=ACAD=AD ∠B = ∠C.∠ADB = ∠ADC
指AD是底边上的高∠BAD = ∠CAD
指AD是顶角平分线观察与猜想——问题源于猜想
填写表格: 由这些重合的线段和角,你能发现等腰三角形的性质吗?说一说你的猜想。
猜想1:等腰三角形的两个底角相等。你能利用已学的公理和定理证明这些猜想吗?猜想2:等腰三角形顶角的角平分线,既是底边上的中线,也是底边上的高。
探知求证:性质1、等腰三角形的两个底角相等。
(等边对等角)已知: △ABC中 AB=AC求证:∠B=∠C2、作△ABC的中线AD,交底边BC于D。探究:已知AB=AC怎样证明∠B = ∠C ?3、作△ABC的高AD,垂直底边BC于D。1、作顶角的平分线AD.D12DD在△ABD和 △ACD中
AB=AC (已知)
∠1=∠2(辅助线作法)
AD=AD(公共边) ∴△ABD≌△ACD(SAS) ∴ ∠B=∠C(全等三角形的对应角相等)证明:作顶角的平分线AD
∴ ∠1=∠2证法欣赏证法一AB=AC ( 已知 ),BD=CD ( 辅助线作法 ),AD=AD (公共边) ,∴ △BAD ≌ △CAD (SSS).∴ ∠ B= ∠C (全等三角形的对应角相等).作底边中线证明: 作底边中线AD.
在△BAD和△CAD中,证法二证明: 作底边高线AD.
AB=AC ( 已知 ),AD=AD (公共边) ,作底边的高线在Rt△BAD和△RtCAD中,证法三∴ Rt △BAD ≌ Rt △CAD (HL).∴ ∠ B= ∠C (全等三角形的对应角相等).在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 用符号语言表示为:12BDCD12ADBCADBCBDCD性质二:
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(三线合一)等腰三角形一个底角为75°,它另外两个角为____ ____
等腰三角形一个角为70°,它的另外两个角为____ ____
已知:等腰三角形的一个角是110 °,则该三角形另外两个角分别是____ ____
练一练35 °和 35 °等腰三角形性质的应用75°和 30° 70°和 40°(或55°和 55°) 如图,△ABC是等腰直角三角形(AB=AC,∠BAC=90°),AD是底边BC上的高,标出∠B、∠C、∠BAD、∠DAC的度数,图中有哪些相等线段? ∠B=∠C=45°
∠BAD=∠DAC=45°AB=AC
AD=BD=CD例2:如图,这是正在修建的南充嘉陵江三桥设计效果图,桥梁支架与桥面形成的△ABC中,AB=AC , AC上有一点D,测得BD=BC=AD,求△ABC 中∠A 的度数.
教学流程解:∵ AB = AC,BD=BC=AD
∴ ∠A BC= ∠C= ∠BDC
∠A= ∠ABD (等边对等角)
设 ∠A =x,则
∠BDC= ∠A + ∠A BD=2X,
所以∠A BC= ∠C= ∠BDC=2x
在△ABC 中,有
∠A+ ∠A BC+ ∠C=x+2x=180 °
解得 x=36 °
∴ ∠A= 36 °,
用一用小结:通过本节课的学习你有收获吗?1、本节课的主要教学知识是等腰三角形的两个性质。等腰三角形的性质内容应用格式性质1ABC性质2ABC等腰三角形的
两个底角相等 等腰三角形的顶角
平分线、底边上的
中线底边上的高
互相重合。∵AB=AC(已知)
∴∠B=∠C (等边对等角)①∵AB=AC,∠1=∠2(已知)
∴BD=DC,AD⊥BC(三线合一)
② ∵AB=AC,BD=DC(已知)
∴ ∠1=∠2, AD⊥BC(三线合一)
③∵ AB=AC, AD⊥BC (已知)
∴ ∠1=∠2, BD=DC(三线合一)D122、本节课学习了数学思想及方法:分类讨论和一题多解。
布置作业 1、P56 习题12.3 1、2、4
2、练习册P22-P23 1—9题
10题为选做题
3、复习课本P49--52
再见
探究活动(1)如图,把一张长方形的纸按图中虚线对折,并减去阴影部分,再把它展开,得到一个什么图形?
(2)你能归纳出等腰三角形的定义吗? (3)你能举出生活中等腰三角形的实例吗? 有两条边相等的三角形叫做等腰三角形. 等腰三角形中,相等的两边叫做腰,
另一边叫做底边, 两腰的夹角叫做
顶角, 腰和底边的夹角 叫做底角.底边基本概念
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示ABC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。
动画演示AC剪出的等腰三角形△ABC是轴对称图形吗?沿折痕对折,找出其中重合的线段和角,填写表格。底角 BD=CD
指AD是底边上中线 AB=ACAD=AD ∠B = ∠C.∠ADB = ∠ADC
指AD是底边上的高∠BAD = ∠CAD
指AD是顶角平分线观察与猜想——问题源于猜想
填写表格: 由这些重合的线段和角,你能发现等腰三角形的性质吗?说一说你的猜想。
猜想1:等腰三角形的两个底角相等。你能利用已学的公理和定理证明这些猜想吗?猜想2:等腰三角形顶角的角平分线,既是底边上的中线,也是底边上的高。
探知求证:性质1、等腰三角形的两个底角相等。
(等边对等角)已知: △ABC中 AB=AC求证:∠B=∠C2、作△ABC的中线AD,交底边BC于D。探究:已知AB=AC怎样证明∠B = ∠C ?3、作△ABC的高AD,垂直底边BC于D。1、作顶角的平分线AD.D12DD在△ABD和 △ACD中
AB=AC (已知)
∠1=∠2(辅助线作法)
AD=AD(公共边) ∴△ABD≌△ACD(SAS) ∴ ∠B=∠C(全等三角形的对应角相等)证明:作顶角的平分线AD
∴ ∠1=∠2证法欣赏证法一AB=AC ( 已知 ),BD=CD ( 辅助线作法 ),AD=AD (公共边) ,∴ △BAD ≌ △CAD (SSS).∴ ∠ B= ∠C (全等三角形的对应角相等).作底边中线证明: 作底边中线AD.
在△BAD和△CAD中,证法二证明: 作底边高线AD.
AB=AC ( 已知 ),AD=AD (公共边) ,作底边的高线在Rt△BAD和△RtCAD中,证法三∴ Rt △BAD ≌ Rt △CAD (HL).∴ ∠ B= ∠C (全等三角形的对应角相等).在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 用符号语言表示为:12BDCD12ADBCADBCBDCD性质二:
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(三线合一)等腰三角形一个底角为75°,它另外两个角为____ ____
等腰三角形一个角为70°,它的另外两个角为____ ____
已知:等腰三角形的一个角是110 °,则该三角形另外两个角分别是____ ____
练一练35 °和 35 °等腰三角形性质的应用75°和 30° 70°和 40°(或55°和 55°) 如图,△ABC是等腰直角三角形(AB=AC,∠BAC=90°),AD是底边BC上的高,标出∠B、∠C、∠BAD、∠DAC的度数,图中有哪些相等线段? ∠B=∠C=45°
∠BAD=∠DAC=45°AB=AC
AD=BD=CD例2:如图,这是正在修建的南充嘉陵江三桥设计效果图,桥梁支架与桥面形成的△ABC中,AB=AC , AC上有一点D,测得BD=BC=AD,求△ABC 中∠A 的度数.
教学流程解:∵ AB = AC,BD=BC=AD
∴ ∠A BC= ∠C= ∠BDC
∠A= ∠ABD (等边对等角)
设 ∠A =x,则
∠BDC= ∠A + ∠A BD=2X,
所以∠A BC= ∠C= ∠BDC=2x
在△ABC 中,有
∠A+ ∠A BC+ ∠C=x+2x=180 °
解得 x=36 °
∴ ∠A= 36 °,
用一用小结:通过本节课的学习你有收获吗?1、本节课的主要教学知识是等腰三角形的两个性质。等腰三角形的性质内容应用格式性质1ABC性质2ABC等腰三角形的
两个底角相等 等腰三角形的顶角
平分线、底边上的
中线底边上的高
互相重合。∵AB=AC(已知)
∴∠B=∠C (等边对等角)①∵AB=AC,∠1=∠2(已知)
∴BD=DC,AD⊥BC(三线合一)
② ∵AB=AC,BD=DC(已知)
∴ ∠1=∠2, AD⊥BC(三线合一)
③∵ AB=AC, AD⊥BC (已知)
∴ ∠1=∠2, BD=DC(三线合一)D122、本节课学习了数学思想及方法:分类讨论和一题多解。
布置作业 1、P56 习题12.3 1、2、4
2、练习册P22-P23 1—9题
10题为选做题
3、复习课本P49--52
再见
