2021-2022学年人教版数学七年级下册 8.3 实际问题与二元一次方程组 课件(共17张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册 8.3 实际问题与二元一次方程组 课件(共17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 225.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 20:27:17 | ||
图片预览






文档简介
(共17张PPT)
第八章 二元一次方程组
8.3 实际问题与二元一次方程组(第1课时)
列一元一次方程解实际问题的步骤是什么?
审
设
列
解
验
答
审题,找出题目中的等量关系;
设未知数;
根据等量关系列方程;
解方程;
验证解是否正确并且是否符合实际意义;
答题。
复习引入
例1:有大小两辆货车,2辆大车与3辆小车一次可以支货15.5吨,5辆大车与6辆小车一次可以支货35吨,求3辆大车与5辆小车一次可以运货多少吨?
等量关系
(1)2辆大车与3辆小车一次可以支货15.5吨
(2)5辆大车与6辆小车一次可以支货35吨
例题讲授
x
x
y
y
解:设1辆大车一次可以支货x吨,1辆小车一次可以支货y吨。
根据题意,得
2x+3y=15.5
5x+6y=35
这个方程解得:
x=4
y=2.5
3辆大车与5辆小车一次可以运货 3x4+5x2.5=24.5(吨)
答:3辆大车与5辆小车一次可以运货24.5吨。
列二元一次方程解实际问题的步骤是什么?
审
设
列
解
验
答
审题,找出题目中的等量关系;
设未知数;
根据等量关系列方程组;
解方程组;
验证解是否正确并且是否符合实际意义;
答题。
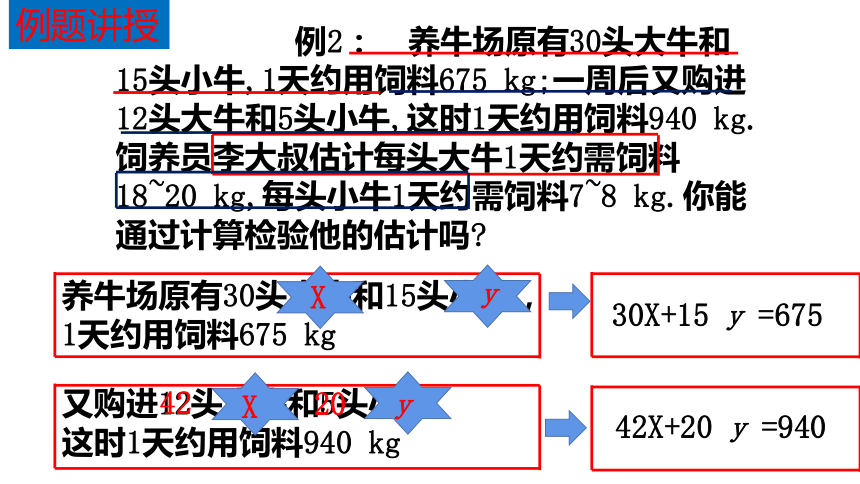
养牛场原有30头大牛和15头小牛,
1天约用饲料675 kg
又购进12头大牛和5头小牛,
这时1天约用饲料940 kg
30X+15 y =675
42X+20 y =940
X
y
X
y
42
20
例2: 养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.你能通过计算检验他的估计吗
例题讲授
解:设每头大牛1天约用饲料x kg,每头小牛1天约用饲料y kg.
答:每头大牛1天约需饲料20 kg,每头小牛1天约需饲料5 kg.因此,饲养员李大叔对大牛的食量估计较准确,对小牛的食量估计偏多.
30 x +15 y =675
(30+12) x +(15+5) y =940
解这个方程组,得
x =20
y =5
实际问题
设未知数、列方程(组)
数学问题
二元一次方程组
解方程组
数学问题的解
二元一次方程组的解
检验
实际问题
的答案
转化
解决实际问题的基本过程
消元
小结
建模
8.3 实际问题与二元一次方程组(第2课时)列二元一次方程组解决配套问题 某车间有90名工人,每人每天平均能生产螺钉15个或螺母24个,要使一个螺钉配套两个螺母,应如何分配工人才能使螺钉和螺母刚好配套?
导入
螺母
螺钉
回忆
列二元一次方程组解应用题的一般步骤:
(1)审题,弄清题中的数量关系
(2)设两个未知数,并用含未知
数的式子表示各自相关的量
(3)根据题中的等量关系列方程组
(4)解方程组,求出未知数的值
(5)检验解的正确性和合理性,写出答案
例题讲解
难点突破
某车间有90名工人,
每人每天平均能生产螺钉15个或螺母24个,
要使一个螺钉配套两个螺母,
应如何分配工人才能使螺钉和螺母刚好配套?
生产螺钉的人数+生产螺母的人数=90
2×螺钉的数量=螺母的数量
螺钉的数量=生产螺钉的人数×15
螺母的数量=生产螺母的人数×24
螺钉:螺母=1:2
x
y
x
y
+
=90
15x
24y
15x
24y
2
×
=
某车间有90名工人,每人每天平均能生产螺钉15个或螺母24个,要使一个螺钉配套两个螺母,应如何分配工人才能使螺钉和螺母刚好配套?
解:设生产螺钉x人,生产螺母y人,根据题意得:
x+y=90
2×15x=24y
答:应分配生产螺钉40人,生产螺母50人才能使螺钉和螺母刚好配套。
解得
x=40
y=50
解题格式展示
课堂练习1.某车间每天能生产甲种零件120个,或者乙种零件100个.甲、乙两种零件分别取3个、2个才能配成一套.要在30天内生产最多的成套产品,问怎样安排生产甲、乙两种零件的天数 2.要用20张白卡纸做包装盒,每张白卡纸可以做盒身两个或者做盒底盖3个.如果一个盒身和两个盒底盖可以做成一个包装盒,那么能否把这白卡纸分成两部分,一部分做盒身,一部分做盒底盖,使做成的盒身和盒底盖正好配套 请设计一种分法.2甲种零件=3乙种零件生产甲种零件天数+生产乙种零件天数=30做盒身的白卡纸数+做盒底盖的白卡纸数=202盒身的数量=盒底盖的数量课堂小结
这节课我们主要探究了如何利用二元一次方程组解决生活中的配套问题。
这类问题中配套的物品之间具有一定的数量关系,这是列方程的重要依据。
谈谈收获
谢谢大家!
第八章 二元一次方程组
8.3 实际问题与二元一次方程组(第1课时)
列一元一次方程解实际问题的步骤是什么?
审
设
列
解
验
答
审题,找出题目中的等量关系;
设未知数;
根据等量关系列方程;
解方程;
验证解是否正确并且是否符合实际意义;
答题。
复习引入
例1:有大小两辆货车,2辆大车与3辆小车一次可以支货15.5吨,5辆大车与6辆小车一次可以支货35吨,求3辆大车与5辆小车一次可以运货多少吨?
等量关系
(1)2辆大车与3辆小车一次可以支货15.5吨
(2)5辆大车与6辆小车一次可以支货35吨
例题讲授
x
x
y
y
解:设1辆大车一次可以支货x吨,1辆小车一次可以支货y吨。
根据题意,得
2x+3y=15.5
5x+6y=35
这个方程解得:
x=4
y=2.5
3辆大车与5辆小车一次可以运货 3x4+5x2.5=24.5(吨)
答:3辆大车与5辆小车一次可以运货24.5吨。
列二元一次方程解实际问题的步骤是什么?
审
设
列
解
验
答
审题,找出题目中的等量关系;
设未知数;
根据等量关系列方程组;
解方程组;
验证解是否正确并且是否符合实际意义;
答题。
养牛场原有30头大牛和15头小牛,
1天约用饲料675 kg
又购进12头大牛和5头小牛,
这时1天约用饲料940 kg
30X+15 y =675
42X+20 y =940
X
y
X
y
42
20
例2: 养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8 kg.你能通过计算检验他的估计吗
例题讲授
解:设每头大牛1天约用饲料x kg,每头小牛1天约用饲料y kg.
答:每头大牛1天约需饲料20 kg,每头小牛1天约需饲料5 kg.因此,饲养员李大叔对大牛的食量估计较准确,对小牛的食量估计偏多.
30 x +15 y =675
(30+12) x +(15+5) y =940
解这个方程组,得
x =20
y =5
实际问题
设未知数、列方程(组)
数学问题
二元一次方程组
解方程组
数学问题的解
二元一次方程组的解
检验
实际问题
的答案
转化
解决实际问题的基本过程
消元
小结
建模
8.3 实际问题与二元一次方程组(第2课时)列二元一次方程组解决配套问题 某车间有90名工人,每人每天平均能生产螺钉15个或螺母24个,要使一个螺钉配套两个螺母,应如何分配工人才能使螺钉和螺母刚好配套?
导入
螺母
螺钉
回忆
列二元一次方程组解应用题的一般步骤:
(1)审题,弄清题中的数量关系
(2)设两个未知数,并用含未知
数的式子表示各自相关的量
(3)根据题中的等量关系列方程组
(4)解方程组,求出未知数的值
(5)检验解的正确性和合理性,写出答案
例题讲解
难点突破
某车间有90名工人,
每人每天平均能生产螺钉15个或螺母24个,
要使一个螺钉配套两个螺母,
应如何分配工人才能使螺钉和螺母刚好配套?
生产螺钉的人数+生产螺母的人数=90
2×螺钉的数量=螺母的数量
螺钉的数量=生产螺钉的人数×15
螺母的数量=生产螺母的人数×24
螺钉:螺母=1:2
x
y
x
y
+
=90
15x
24y
15x
24y
2
×
=
某车间有90名工人,每人每天平均能生产螺钉15个或螺母24个,要使一个螺钉配套两个螺母,应如何分配工人才能使螺钉和螺母刚好配套?
解:设生产螺钉x人,生产螺母y人,根据题意得:
x+y=90
2×15x=24y
答:应分配生产螺钉40人,生产螺母50人才能使螺钉和螺母刚好配套。
解得
x=40
y=50
解题格式展示
课堂练习1.某车间每天能生产甲种零件120个,或者乙种零件100个.甲、乙两种零件分别取3个、2个才能配成一套.要在30天内生产最多的成套产品,问怎样安排生产甲、乙两种零件的天数 2.要用20张白卡纸做包装盒,每张白卡纸可以做盒身两个或者做盒底盖3个.如果一个盒身和两个盒底盖可以做成一个包装盒,那么能否把这白卡纸分成两部分,一部分做盒身,一部分做盒底盖,使做成的盒身和盒底盖正好配套 请设计一种分法.2甲种零件=3乙种零件生产甲种零件天数+生产乙种零件天数=30做盒身的白卡纸数+做盒底盖的白卡纸数=202盒身的数量=盒底盖的数量课堂小结
这节课我们主要探究了如何利用二元一次方程组解决生活中的配套问题。
这类问题中配套的物品之间具有一定的数量关系,这是列方程的重要依据。
谈谈收获
谢谢大家!
