青岛版小学五年级数学上册《质数、合数和分解质因数》教学建议
文档属性
| 名称 | 青岛版小学五年级数学上册《质数、合数和分解质因数》教学建议 | 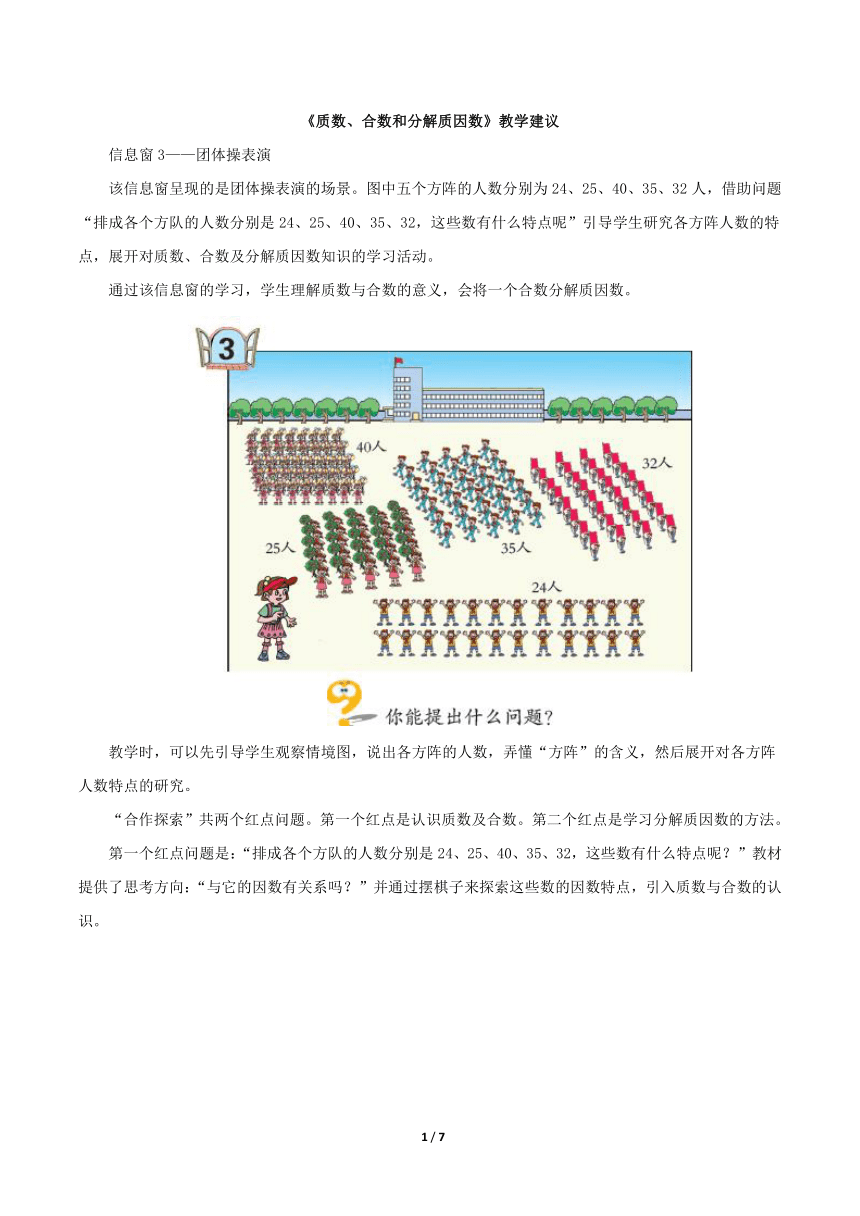 | |
| 格式 | doc | ||
| 文件大小 | 600.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 20:20:51 | ||
图片预览


文档简介
《质数、合数和分解质因数》教学建议
信息窗3——团体操表演
该信息窗呈现的是团体操表演的场景。图中五个方阵的人数分别为24、25、40、35、32人,借助问题“排成各个方队的人数分别是24、25、40、35、32,这些数有什么特点呢”引导学生研究各方阵人数的特点,展开对质数、合数及分解质因数知识的学习活动。
通过该信息窗的学习,学生理解质数与合数的意义,会将一个合数分解质因数。
教学时,可以先引导学生观察情境图,说出各方阵的人数,弄懂“方阵”的含义,然后展开对各方阵人数特点的研究。
“合作探索”共两个红点问题。第一个红点是认识质数及合数。第二个红点是学习分解质因数的方法。
第一个红点问题是:“排成各个方队的人数分别是24、25、40、35、32,这些数有什么特点呢?”教材提供了思考方向:“与它的因数有关系吗?”并通过摆棋子来探索这些数的因数特点,引入质数与合数的认识。
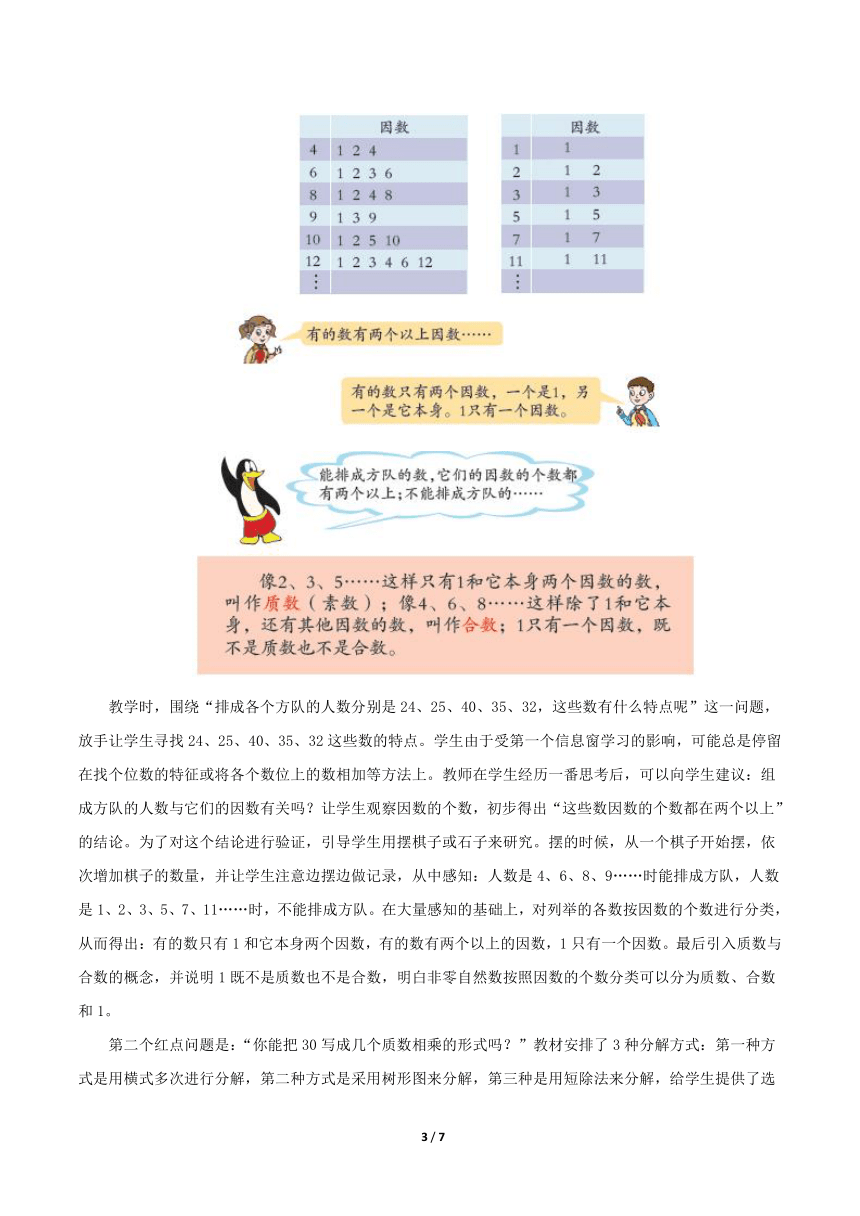
教学时,围绕“排成各个方队的人数分别是24、25、40、35、32,这些数有什么特点呢”这一问题,放手让学生寻找24、25、40、35、32这些数的特点。学生由于受第一个信息窗学习的影响,可能总是停留在找个位数的特征或将各个数位上的数相加等方法上。教师在学生经历一番思考后,可以向学生建议:组成方队的人数与它们的因数有关吗?让学生观察因数的个数,初步得出“这些数因数的个数都在两个以上”的结论。为了对这个结论进行验证,引导学生用摆棋子或石子来研究。摆的时候,从一个棋子开始摆,依次增加棋子的数量,并让学生注意边摆边做记录,从中感知:人数是4、6、8、9……时能排成方队,人数是1、2、3、5、7、11……时,不能排成方队。在大量感知的基础上,对列举的各数按因数的个数进行分类,从而得出:有的数只有1和它本身两个因数,有的数有两个以上的因数,1只有一个因数。最后引入质数与合数的概念,并说明1既不是质数也不是合数,明白非零自然数按照因数的个数分类可以分为质数、合数和1。
第二个红点问题是:“你能把30写成几个质数相乘的形式吗?”教材安排了3种分解方式:第一种方式是用横式多次进行分解,第二种方式是采用树形图来分解,第三种是用短除法来分解,给学生提供了选择的空间。
教学时,可以先让学生独立尝试把一个合数写成几个质数相乘的形式。当学生遇到困难时,教师可以把教材中找一个合数的质因数的3种方法介绍给学生,并结合算式说明什么是分解质因数,然后通过讨论,实现分解方法的优化。
“自主练习”第1、2题都是巩固质数与合数概念的练习。练习时,可以让学生独立解决,然后进行交流反馈。交流时,重点说明选择质数或合数的方法。注意第2题最后一问,应先思考11~20中的奇数有哪些,再从这些奇数中寻找合数。
第3题是一道辨别对错的题目。学生练习后,教师要注意引导学生明确以下两点:一是非零自然数的两种分类方法;二是奇数、偶数、质数、合数的区别与联系。
第4题与第5题是分解质因数的相关练习。练习时,可以让学生独立完成,交流时应让学生进一步明确,虽然分解质因数的形式不同,但是都要注意两点:一是把合数写成连乘的形式,二是每个因数必须是质数。
第6题是判断对错的题,进一步巩固分解质因数的含义。
第7题是以交流对话的形式巩固数的特征的练习。练习时,引导学生从多角度描述数的特征,加深对本单元基本概念的巩固。练习可以在同桌间进行,也可以在小组内进行,注意卡片上的数应限制在100以内。
第8题,教学时让学生分别划掉2、3、5、7的倍数,可以让学生圈一圈或用不同颜色的笔画一画,为便于观察,可以把剩下的数按相应的位置写下来,这时再引导学生观察,便会有所发现,即剩下的数都是质数,它们构成50以内的质数表。
第9题是解决实际问题。练习时,要引导学生将本题转化为判断“40是否是5的倍数”等数学问题。
第10题是一道借助找特别数巩固自然数特征的题目。练习时,先让学生根据自然数的特征独立找出各组数中与众不同的数,然后引导学生交流结果和理由,只要学生说得有道理,都应给予肯定。
第11题是一道拓展知识的练习题。练习时,可以让学生独立填数,并找规律。交流后,教师可以向学生简单介绍有关“哥德巴赫猜想”的知识,初步了解合数的特点。
第12题是一道游戏性的应用题。练习时,可以先让学生独立思考,找出答案后,再进行交流。教师可以多补充相关的内容,以游戏的形式帮助学生理解巩固本单元所学的基本概念。
“我学会了吗”第1题复习2、5、3的倍数特征。第2题是一道综合应用题,练习时,先让学生根据所学知识独立确定每一个字母代表的数,并做好记录,最后交流。交流时,注意引导学生结合所学数的特征说明判断的理由。
1 / 7
信息窗3——团体操表演
该信息窗呈现的是团体操表演的场景。图中五个方阵的人数分别为24、25、40、35、32人,借助问题“排成各个方队的人数分别是24、25、40、35、32,这些数有什么特点呢”引导学生研究各方阵人数的特点,展开对质数、合数及分解质因数知识的学习活动。
通过该信息窗的学习,学生理解质数与合数的意义,会将一个合数分解质因数。
教学时,可以先引导学生观察情境图,说出各方阵的人数,弄懂“方阵”的含义,然后展开对各方阵人数特点的研究。
“合作探索”共两个红点问题。第一个红点是认识质数及合数。第二个红点是学习分解质因数的方法。
第一个红点问题是:“排成各个方队的人数分别是24、25、40、35、32,这些数有什么特点呢?”教材提供了思考方向:“与它的因数有关系吗?”并通过摆棋子来探索这些数的因数特点,引入质数与合数的认识。
教学时,围绕“排成各个方队的人数分别是24、25、40、35、32,这些数有什么特点呢”这一问题,放手让学生寻找24、25、40、35、32这些数的特点。学生由于受第一个信息窗学习的影响,可能总是停留在找个位数的特征或将各个数位上的数相加等方法上。教师在学生经历一番思考后,可以向学生建议:组成方队的人数与它们的因数有关吗?让学生观察因数的个数,初步得出“这些数因数的个数都在两个以上”的结论。为了对这个结论进行验证,引导学生用摆棋子或石子来研究。摆的时候,从一个棋子开始摆,依次增加棋子的数量,并让学生注意边摆边做记录,从中感知:人数是4、6、8、9……时能排成方队,人数是1、2、3、5、7、11……时,不能排成方队。在大量感知的基础上,对列举的各数按因数的个数进行分类,从而得出:有的数只有1和它本身两个因数,有的数有两个以上的因数,1只有一个因数。最后引入质数与合数的概念,并说明1既不是质数也不是合数,明白非零自然数按照因数的个数分类可以分为质数、合数和1。
第二个红点问题是:“你能把30写成几个质数相乘的形式吗?”教材安排了3种分解方式:第一种方式是用横式多次进行分解,第二种方式是采用树形图来分解,第三种是用短除法来分解,给学生提供了选择的空间。
教学时,可以先让学生独立尝试把一个合数写成几个质数相乘的形式。当学生遇到困难时,教师可以把教材中找一个合数的质因数的3种方法介绍给学生,并结合算式说明什么是分解质因数,然后通过讨论,实现分解方法的优化。
“自主练习”第1、2题都是巩固质数与合数概念的练习。练习时,可以让学生独立解决,然后进行交流反馈。交流时,重点说明选择质数或合数的方法。注意第2题最后一问,应先思考11~20中的奇数有哪些,再从这些奇数中寻找合数。
第3题是一道辨别对错的题目。学生练习后,教师要注意引导学生明确以下两点:一是非零自然数的两种分类方法;二是奇数、偶数、质数、合数的区别与联系。
第4题与第5题是分解质因数的相关练习。练习时,可以让学生独立完成,交流时应让学生进一步明确,虽然分解质因数的形式不同,但是都要注意两点:一是把合数写成连乘的形式,二是每个因数必须是质数。
第6题是判断对错的题,进一步巩固分解质因数的含义。
第7题是以交流对话的形式巩固数的特征的练习。练习时,引导学生从多角度描述数的特征,加深对本单元基本概念的巩固。练习可以在同桌间进行,也可以在小组内进行,注意卡片上的数应限制在100以内。
第8题,教学时让学生分别划掉2、3、5、7的倍数,可以让学生圈一圈或用不同颜色的笔画一画,为便于观察,可以把剩下的数按相应的位置写下来,这时再引导学生观察,便会有所发现,即剩下的数都是质数,它们构成50以内的质数表。
第9题是解决实际问题。练习时,要引导学生将本题转化为判断“40是否是5的倍数”等数学问题。
第10题是一道借助找特别数巩固自然数特征的题目。练习时,先让学生根据自然数的特征独立找出各组数中与众不同的数,然后引导学生交流结果和理由,只要学生说得有道理,都应给予肯定。
第11题是一道拓展知识的练习题。练习时,可以让学生独立填数,并找规律。交流后,教师可以向学生简单介绍有关“哥德巴赫猜想”的知识,初步了解合数的特点。
第12题是一道游戏性的应用题。练习时,可以先让学生独立思考,找出答案后,再进行交流。教师可以多补充相关的内容,以游戏的形式帮助学生理解巩固本单元所学的基本概念。
“我学会了吗”第1题复习2、5、3的倍数特征。第2题是一道综合应用题,练习时,先让学生根据所学知识独立确定每一个字母代表的数,并做好记录,最后交流。交流时,注意引导学生结合所学数的特征说明判断的理由。
1 / 7
