华师大版数学八下 17.3.2.2一次函数的图像的实际问题 课件(共20张)
文档属性
| 名称 | 华师大版数学八下 17.3.2.2一次函数的图像的实际问题 课件(共20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 484.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 20:54:21 | ||
图片预览







文档简介
(共20张PPT)
第2课时 实际问题中的一次函数图象
华东师大版八年级数学下册
乌鸦喝水,是《伊索寓言》中一个有趣的寓言故
事.故事梗概为:"一只口渴的乌鸦看到窄口瓶内有半瓶
水,于是将小石子投入瓶中,使水面升高,从而喝到
了水."告诉人们遇到困难要积极想解决办法,认真思
考才能让问题迎刃而解的道理.数学问题也一样哦.
情景引入
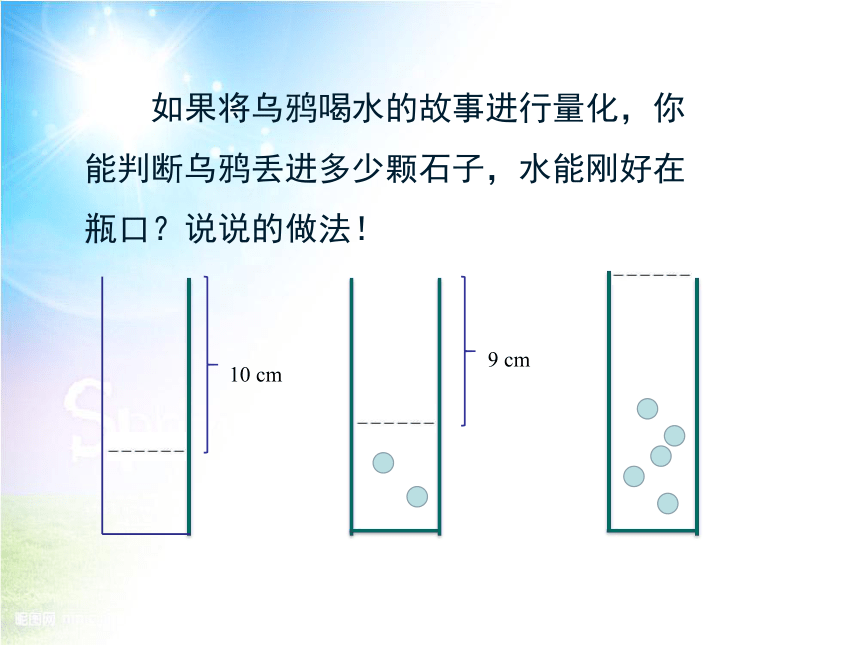
10 cm
9 cm
如果将乌鸦喝水的故事进行量化,你能判断乌鸦丢进多少颗石子,水能刚好在瓶口?说说的做法!
新课探索
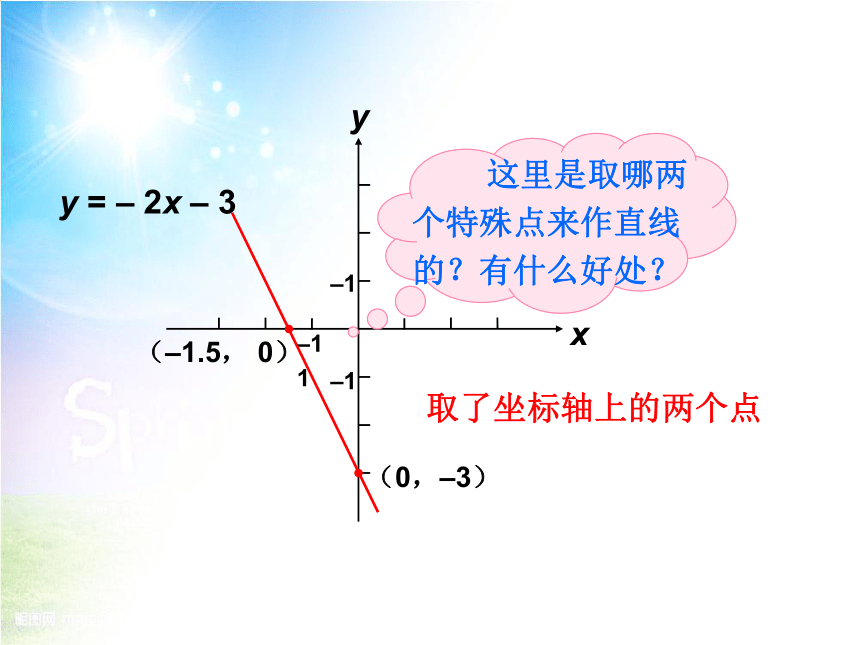
例 1 求直线 y = – 2x – 3 与 x 轴和 y 轴的交点,并画出这条直线.
分析:x 轴上的点的纵坐标等于 0,y 轴上的点的横坐标等于 0. 交点同时在直线 y = – 2x – 3 上
x
y
–1 1
–1
–1
(–1.5, 0)
(0,–3)
y = – 2x – 3
这里是取哪两个特殊点来作直线的?有什么好处?
取了坐标轴上的两个点
已知直线, , 当
为何值时直线
(1)经过原点
(2)与 轴相交于点(0,2)
(3)与 轴相交于点(2,0)
试一试
试一试
1、一次函数y=x+1的图象是 ,一般取两点 , 。
2、正比例函数y=5x的图象是 ,一般取两点 , 。
3、把直线y=x+1向下平移3个单位长度得到的函数解析为 。
y=x-2
总
结
直线 y = kx + b (k ≠ 0) 与坐标轴的交点
与 x 轴的交点坐标为( – ,0)
b
k
与 y 轴的交点坐标为(0,b)
方程 kx + b = 0 的解是 x = –
b
k
练习
1、求下列直线与 x 轴和 y 轴的交点,并在同一个平面直角坐标系中画出它们的图象:
(1)y = 4x – 1; (2)y = – x + 2.
2
3
解(1)与 x 轴的交点是( ,0),与 y 轴的交点是(0,–1).
(2)与 x 轴的交点是(3,0),与 y 轴的交点是(0,2).
1
4
x
y
–1 1
–1
–1
y = 4x – 1
y = – x + 2
2
3
( ,0)
1
4
(0,–1)
(3,0)
(0,2 )
例 3 问题 1 中,汽车距北京的路程 s(千米)与汽车在高速公路上行驶的时间 t (时)之间的函数关系式是 s = 570 – 95t,试画出这个函数的图象.
t(时)
s(千米)
O 1 2 3 4 5 6 7
570475
380
285
190
95
这里自变量 t 的取值范围是什么?
0 ≤ t ≤ 6
函数图象是一条线段.
总
结
当 x ≤ a 或 x ≥ a 时,函数 y = kx + b 的图象是一条射线;
当 a ≤ x < c (a < c) 时,函数 y = kx + b 的图象是一条线段;
当 x 取几个整数时,函数 y = kx + b 的图象是一条直线上的几个点.
2、某企业去年积压产品a件(a>0),今年预计每月销售产
品2b件,同时每月可生产出产品b个,若产品积压量y(件)
是今年开工时间(月)的函数,则它的图象只能是( )
练习
3、拖拉机开始工作时,油箱中有油24L,每小时耗油4L,那么油箱中剩余原油量y(L)与工作时间x(h)之间的函数关系式和图象是( )
A. y=4x-24(0≤x ≤ 6) B. y=24-4x
C. y=24-4x (0≤x ≤ 6 ) D. y=-24+4x
练习
-3
14
O
一次函数y=kx+b 的图象是一条直线,我们称为直线y=kx+b。
正比例函数y=kx 的图象是一条过原点的直线。
因此,在作一次函数图像时,只要描出适合关系式的两点(0, b )、( ,0) ,再连接两点即可。
正比例函数的图象找(0, 0)(1 ,k)两点画直线。
课堂小结
当堂练习
1. 已知一次函数 y = mx –(m – 2)过原点,则 m 的值为( )
A. m>2 B. m<2
C. m = 2 D. 不能确定
C
2. 函数 y = kx + b 的图象平行于直线 y = – 2x,且与 y 轴交于点(0,3),则
k = _____,b = _____ .
3
– 2
3. 如图,直线 y = 2x + 4 与 x 轴相交于点 A,与 y 轴相交于点 B.
(1)求 A,B 两点的坐标;
(2)求△ABO 的面积.
A
B
O
1
1
x
y
解(1)当 y = 0 时,x = – 2,所以点 A(–2,0),
当 x = 0 时,y = 4,所以点 B(0,4).
(2)S△ABC = ×2×4 = 4
1
2
4. 一辆汽车以每小时 80 km 的速度从甲地开往 320 km外的乙地.
(1)写出汽车离甲地的距离 s1 (km) 与行驶时间 t (h) 之间的函数关系式,并画出该函数的图象;
(2)写出汽车离乙地的距离 s2(km) 与行驶时间 t (h) 之间的函数关系式,并画出该函数的图象.
解(1)s1 = 80t
(2)s2 = 320 – 80t
t(h)
s(km)
O 1 2 3 4 5
320
240
160
80
(4,320)
(0,320)
(4,0)
x/ 吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
5. 如图,l1反映了某公司产品的销售收入与销售量的关系,
l1
l2
(1)当销售量为2吨时,销售收入= 元,
销售成本= 元;
2000
3000
l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:
x/ 吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1
l2
(2)当销售量为6吨时,销售收入= 元,
销售成本= 元;
6000
5000
(3)当销售量为 时,销售收入等于销售成本;
4吨
第2课时 实际问题中的一次函数图象
华东师大版八年级数学下册
乌鸦喝水,是《伊索寓言》中一个有趣的寓言故
事.故事梗概为:"一只口渴的乌鸦看到窄口瓶内有半瓶
水,于是将小石子投入瓶中,使水面升高,从而喝到
了水."告诉人们遇到困难要积极想解决办法,认真思
考才能让问题迎刃而解的道理.数学问题也一样哦.
情景引入
10 cm
9 cm
如果将乌鸦喝水的故事进行量化,你能判断乌鸦丢进多少颗石子,水能刚好在瓶口?说说的做法!
新课探索
例 1 求直线 y = – 2x – 3 与 x 轴和 y 轴的交点,并画出这条直线.
分析:x 轴上的点的纵坐标等于 0,y 轴上的点的横坐标等于 0. 交点同时在直线 y = – 2x – 3 上
x
y
–1 1
–1
–1
(–1.5, 0)
(0,–3)
y = – 2x – 3
这里是取哪两个特殊点来作直线的?有什么好处?
取了坐标轴上的两个点
已知直线, , 当
为何值时直线
(1)经过原点
(2)与 轴相交于点(0,2)
(3)与 轴相交于点(2,0)
试一试
试一试
1、一次函数y=x+1的图象是 ,一般取两点 , 。
2、正比例函数y=5x的图象是 ,一般取两点 , 。
3、把直线y=x+1向下平移3个单位长度得到的函数解析为 。
y=x-2
总
结
直线 y = kx + b (k ≠ 0) 与坐标轴的交点
与 x 轴的交点坐标为( – ,0)
b
k
与 y 轴的交点坐标为(0,b)
方程 kx + b = 0 的解是 x = –
b
k
练习
1、求下列直线与 x 轴和 y 轴的交点,并在同一个平面直角坐标系中画出它们的图象:
(1)y = 4x – 1; (2)y = – x + 2.
2
3
解(1)与 x 轴的交点是( ,0),与 y 轴的交点是(0,–1).
(2)与 x 轴的交点是(3,0),与 y 轴的交点是(0,2).
1
4
x
y
–1 1
–1
–1
y = 4x – 1
y = – x + 2
2
3
( ,0)
1
4
(0,–1)
(3,0)
(0,2 )
例 3 问题 1 中,汽车距北京的路程 s(千米)与汽车在高速公路上行驶的时间 t (时)之间的函数关系式是 s = 570 – 95t,试画出这个函数的图象.
t(时)
s(千米)
O 1 2 3 4 5 6 7
570475
380
285
190
95
这里自变量 t 的取值范围是什么?
0 ≤ t ≤ 6
函数图象是一条线段.
总
结
当 x ≤ a 或 x ≥ a 时,函数 y = kx + b 的图象是一条射线;
当 a ≤ x < c (a < c) 时,函数 y = kx + b 的图象是一条线段;
当 x 取几个整数时,函数 y = kx + b 的图象是一条直线上的几个点.
2、某企业去年积压产品a件(a>0),今年预计每月销售产
品2b件,同时每月可生产出产品b个,若产品积压量y(件)
是今年开工时间(月)的函数,则它的图象只能是( )
练习
3、拖拉机开始工作时,油箱中有油24L,每小时耗油4L,那么油箱中剩余原油量y(L)与工作时间x(h)之间的函数关系式和图象是( )
A. y=4x-24(0≤x ≤ 6) B. y=24-4x
C. y=24-4x (0≤x ≤ 6 ) D. y=-24+4x
练习
-3
14
O
一次函数y=kx+b 的图象是一条直线,我们称为直线y=kx+b。
正比例函数y=kx 的图象是一条过原点的直线。
因此,在作一次函数图像时,只要描出适合关系式的两点(0, b )、( ,0) ,再连接两点即可。
正比例函数的图象找(0, 0)(1 ,k)两点画直线。
课堂小结
当堂练习
1. 已知一次函数 y = mx –(m – 2)过原点,则 m 的值为( )
A. m>2 B. m<2
C. m = 2 D. 不能确定
C
2. 函数 y = kx + b 的图象平行于直线 y = – 2x,且与 y 轴交于点(0,3),则
k = _____,b = _____ .
3
– 2
3. 如图,直线 y = 2x + 4 与 x 轴相交于点 A,与 y 轴相交于点 B.
(1)求 A,B 两点的坐标;
(2)求△ABO 的面积.
A
B
O
1
1
x
y
解(1)当 y = 0 时,x = – 2,所以点 A(–2,0),
当 x = 0 时,y = 4,所以点 B(0,4).
(2)S△ABC = ×2×4 = 4
1
2
4. 一辆汽车以每小时 80 km 的速度从甲地开往 320 km外的乙地.
(1)写出汽车离甲地的距离 s1 (km) 与行驶时间 t (h) 之间的函数关系式,并画出该函数的图象;
(2)写出汽车离乙地的距离 s2(km) 与行驶时间 t (h) 之间的函数关系式,并画出该函数的图象.
解(1)s1 = 80t
(2)s2 = 320 – 80t
t(h)
s(km)
O 1 2 3 4 5
320
240
160
80
(4,320)
(0,320)
(4,0)
x/ 吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
5. 如图,l1反映了某公司产品的销售收入与销售量的关系,
l1
l2
(1)当销售量为2吨时,销售收入= 元,
销售成本= 元;
2000
3000
l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:
x/ 吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1
l2
(2)当销售量为6吨时,销售收入= 元,
销售成本= 元;
6000
5000
(3)当销售量为 时,销售收入等于销售成本;
4吨
