17.5 其他实际问题 课件(共13张PPT)
文档属性
| 名称 | 17.5 其他实际问题 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
17.5其他实际问题
导入新课:
情景引入
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
分析
1
第一轮传染后
1+x
第二轮传染后
1+x+x(1+x)
设每轮传染中平均一个人传染了x个人.
开始有一人患了流感,第一轮的传染源就是这个人,他传染了x个人,用代数式表示,第一轮后共有__________人患了流感;第二轮传染中,这些人中的每个人又传染了x个人,
用代数式表示,第二轮后共有_____________________人患了流感.
(x+1)
1+x+x(1+x)
1+x+x(1+x)=121
解方程,得
答:平均一个人传染了________个人.
10
-12
(不合题意,舍去)
10
探究1:
如果按照这样的传染速度,
三轮传染后有多少人患流感
121+121×10=1331人
你能快速写出吗
例1.电脑勒索病毒的传播非常快,如果开始有6台电脑被感染,经过两轮感染后共有2400台电脑被感染. 每轮感染中平均一台电脑会感染几台电脑?
解:设每轮感染中平均一台电脑会感染x台电脑.
答:每轮感染中平均一台电脑会感染19台电脑;
解得x1=19 或 x2=-21 (舍去)
依题意 6+6x+6x (1+x) =2400
6 (1+x)2 =2400
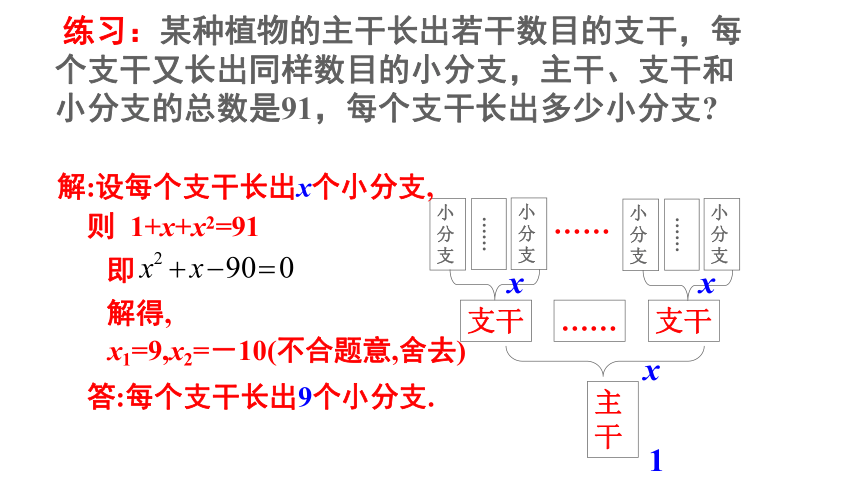
练习:某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少小分支
主干
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
x
1
解:设每个支干长出x个小分支,
则 1+x+x2=91
即
解得,
x1=9,x2=-10(不合题意,舍去)
答:每个支干长出9个小分支.
利润问题
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进价不变的情况下,若每千克涨价0.5元,日销售量将减少10千克,现该商场要保证每天盈利6000元,同时又让顾客得到实惠,那么每千克应涨价多少元
每千克的盈利×每天的销售量=每天的盈利
解:设每千克应涨价x元.
由题意得:
(10+x)(500-20x)=6000
解得: x1=5,x2=10
因为为了使顾客得到实惠,所以x=5
答:每千克应涨价5元.
(10+x)元
(500-20x)千克
6000元
例2 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,尽快减少库存,商场决定采取适当的降价措施。经调查发现,如果每件衬衫降价1元,商场平均每天可多售出2件。若商场平均每天销售这种衬衫的盈利要达到1200元,每件衬衫应降价多少元?
解:设每件衬衫应降价X元
根据题意得:(40-x)(20+2x)=1200
∴ x2-30x+200=0
解之得:x1=10, x2=20
而商场为了尽快减少库存
∴ x=20
答:每件应降价20元
1.某商场礼品柜台春节期间购进大量贺年片,一种贺年片平均每天能售出500张,每张盈利0.3元.为了尽快减少库存,商场决定采取适当的降价措施.调查表明:当销售价每降价0.1元时,其销售量就将多售出100张.商场要想平均每天盈利达到120元,每张贺年片应降价多少元
随堂练习
解:设每张贺年卡应降价x元,根据题意,得
x
0.1
(0.3-x)(500+100· )=120
解这个方程得:100x2+20x-3=0
x1=0.1,x2=-0.3(不合题意,舍去)
答:每张贺卡应降价0.1元
例3:有一个两位数,它的两个数字之和是8,把这个两位数的数字交换位置后所得的数乘以原来的数就得到1855,求原来的两位数。
解:设原来的两位数的个位数字为x,则十位上的数字为8-x,根据题意得:
[10(8-x)+x][10x+(8-x)]=1855
整理后得: x2-8x+15=0
解这个方程得:x1=3 x2=5
答:原来的两位数为35或53.
单循环
双循环
明德天心中学初二年级组织一次足球赛,赛制为单循环形式(每两队之间赛一场),20个班各派出一支队伍参赛,需安排 场比赛?
明德天心中学初二年级组织一次足球赛,赛制为双循环形式(每两队之间赛两场,分别作为主场和客场),20个班各派出一支队伍参赛,
需安排 场比赛?
如果x支队伍参加比赛呢?
例4 在一次聚会中,每两个参加聚会的人都相互握了一次手,一共握了45次手,问参加这次聚会的人数是多少?
例6 一组学生组织春游,预计共需费用120元.后来又有2人参加进来,费用不变,这样每人可少分摊3元.问原来这组学生的人数是多少
分析:设原来这组学生的人数是x人,则把体重信息整理成下表:
总费用/元 人数/人 每人费用/元
原来
现在
解:设原来这组学生的人数是x人,由题意得,
两边同乘x(x+2),整理,得,
x2+2x-80=0.
解这个方程,得,
x1=-10,x2=8.
经检验x1=-10,x2=8都是原方程的根,但x1=-10不符合题意,所以取x=8.
答:原来这组学生是8人.
解分式方程应用题时,所得根不仅要检验根是否为增根,还要考虑它是否符合题意.
方法点拨
17.5其他实际问题
导入新课:
情景引入
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
分析
1
第一轮传染后
1+x
第二轮传染后
1+x+x(1+x)
设每轮传染中平均一个人传染了x个人.
开始有一人患了流感,第一轮的传染源就是这个人,他传染了x个人,用代数式表示,第一轮后共有__________人患了流感;第二轮传染中,这些人中的每个人又传染了x个人,
用代数式表示,第二轮后共有_____________________人患了流感.
(x+1)
1+x+x(1+x)
1+x+x(1+x)=121
解方程,得
答:平均一个人传染了________个人.
10
-12
(不合题意,舍去)
10
探究1:
如果按照这样的传染速度,
三轮传染后有多少人患流感
121+121×10=1331人
你能快速写出吗
例1.电脑勒索病毒的传播非常快,如果开始有6台电脑被感染,经过两轮感染后共有2400台电脑被感染. 每轮感染中平均一台电脑会感染几台电脑?
解:设每轮感染中平均一台电脑会感染x台电脑.
答:每轮感染中平均一台电脑会感染19台电脑;
解得x1=19 或 x2=-21 (舍去)
依题意 6+6x+6x (1+x) =2400
6 (1+x)2 =2400
练习:某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少小分支
主干
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
x
1
解:设每个支干长出x个小分支,
则 1+x+x2=91
即
解得,
x1=9,x2=-10(不合题意,舍去)
答:每个支干长出9个小分支.
利润问题
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进价不变的情况下,若每千克涨价0.5元,日销售量将减少10千克,现该商场要保证每天盈利6000元,同时又让顾客得到实惠,那么每千克应涨价多少元
每千克的盈利×每天的销售量=每天的盈利
解:设每千克应涨价x元.
由题意得:
(10+x)(500-20x)=6000
解得: x1=5,x2=10
因为为了使顾客得到实惠,所以x=5
答:每千克应涨价5元.
(10+x)元
(500-20x)千克
6000元
例2 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,尽快减少库存,商场决定采取适当的降价措施。经调查发现,如果每件衬衫降价1元,商场平均每天可多售出2件。若商场平均每天销售这种衬衫的盈利要达到1200元,每件衬衫应降价多少元?
解:设每件衬衫应降价X元
根据题意得:(40-x)(20+2x)=1200
∴ x2-30x+200=0
解之得:x1=10, x2=20
而商场为了尽快减少库存
∴ x=20
答:每件应降价20元
1.某商场礼品柜台春节期间购进大量贺年片,一种贺年片平均每天能售出500张,每张盈利0.3元.为了尽快减少库存,商场决定采取适当的降价措施.调查表明:当销售价每降价0.1元时,其销售量就将多售出100张.商场要想平均每天盈利达到120元,每张贺年片应降价多少元
随堂练习
解:设每张贺年卡应降价x元,根据题意,得
x
0.1
(0.3-x)(500+100· )=120
解这个方程得:100x2+20x-3=0
x1=0.1,x2=-0.3(不合题意,舍去)
答:每张贺卡应降价0.1元
例3:有一个两位数,它的两个数字之和是8,把这个两位数的数字交换位置后所得的数乘以原来的数就得到1855,求原来的两位数。
解:设原来的两位数的个位数字为x,则十位上的数字为8-x,根据题意得:
[10(8-x)+x][10x+(8-x)]=1855
整理后得: x2-8x+15=0
解这个方程得:x1=3 x2=5
答:原来的两位数为35或53.
单循环
双循环
明德天心中学初二年级组织一次足球赛,赛制为单循环形式(每两队之间赛一场),20个班各派出一支队伍参赛,需安排 场比赛?
明德天心中学初二年级组织一次足球赛,赛制为双循环形式(每两队之间赛两场,分别作为主场和客场),20个班各派出一支队伍参赛,
需安排 场比赛?
如果x支队伍参加比赛呢?
例4 在一次聚会中,每两个参加聚会的人都相互握了一次手,一共握了45次手,问参加这次聚会的人数是多少?
例6 一组学生组织春游,预计共需费用120元.后来又有2人参加进来,费用不变,这样每人可少分摊3元.问原来这组学生的人数是多少
分析:设原来这组学生的人数是x人,则把体重信息整理成下表:
总费用/元 人数/人 每人费用/元
原来
现在
解:设原来这组学生的人数是x人,由题意得,
两边同乘x(x+2),整理,得,
x2+2x-80=0.
解这个方程,得,
x1=-10,x2=8.
经检验x1=-10,x2=8都是原方程的根,但x1=-10不符合题意,所以取x=8.
答:原来这组学生是8人.
解分式方程应用题时,所得根不仅要检验根是否为增根,还要考虑它是否符合题意.
方法点拨
