2021-2022年北师大版七年级数学下册2.3平行线的性质解答题优生辅导训练(Word版含答案)
文档属性
| 名称 | 2021-2022年北师大版七年级数学下册2.3平行线的性质解答题优生辅导训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 459.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 21:25:16 | ||
图片预览




文档简介
2021-2022年北师大版七年级数学下册《2-3平行线的性质》解答题优生辅导训练(附答案)
1.如图,已知∠ABC+∠ECB=180°,∠P=∠Q,则∠1与∠2是否相等?说说你的理由.
2.如图,BE平分∠ABC交CD的延长线于E,∠ABC=2∠E,∠ADE=∠BCD.
(1)请说明AB∥EF的理由;
(2)若AF平分∠BAD交DC的延长线于F,判断AF与BE的位置关系,并说明理由.
3.如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说明理由.
(提示:三角形的内角和等于180°)
①填空或填写理由
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°
∵AB∥CD,EF∥AB,
∴ ∥ ,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+ =180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
③观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B、∠D的关系,不说明理由.
4.课题学行线的“等角转化”功能.
阅读理解:
如图1,已知点A是BC外一点,连接AB,AC.求∠BAC+∠B+∠C的度数.
(1)阅读并补充下面推理过程.
解:过点A作ED∥BC,所以∠B= ,∠C= .
又因为∠EAB+∠BAC+∠DAC=180°.所以∠B+∠BAC+∠C=180°.
解题反思:
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
方法运用:
(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.
提示:过点C作CF∥AB.
深化拓展:
(3)已知AB∥CD,点C在点D的右侧,∠ADC=70°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.
如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为 °.
5.(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?
(3)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(4)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?
6.(1)请在横线上填写合适的内容,完成下面的证明:
如图①,如果AB∥CD,求证:∠APC=∠A+∠C.
证明:过P作PM∥AB.
∴∠A=∠APM,( )
∵PM∥AB,AB∥CD(已知)
∴PM∥CD,( )
∴∠C= ( )
∵∠APC=∠APM+∠CPM,
∴∠APC=∠A+∠C(等量代换)
(2)如图②,AB∥CD,直接写出∠A+∠P+∠Q+∠C= .
(3)如图③,AB∥CD,若∠ABP=x,∠BPQ=y,∠PQC=z,∠QCD=m,你能用x,y,z表示m的大小吗?试说明理由.
7.某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论运用很广,请你利用这个结论解决以下问题:
已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.
(1)如图1,运用上述结论,探究∠PEQ与∠APE+∠CQE之间的数量关系.并说明理由;
(2)如图2,PF平分∠BPE,QF平分∠EQD,当∠PEQ=130°时,求出∠PFQ的度数;
(3)如图3,若点E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延长线交PF于点F,当∠PEQ=80°时,请直接写出∠PFQ的度数.
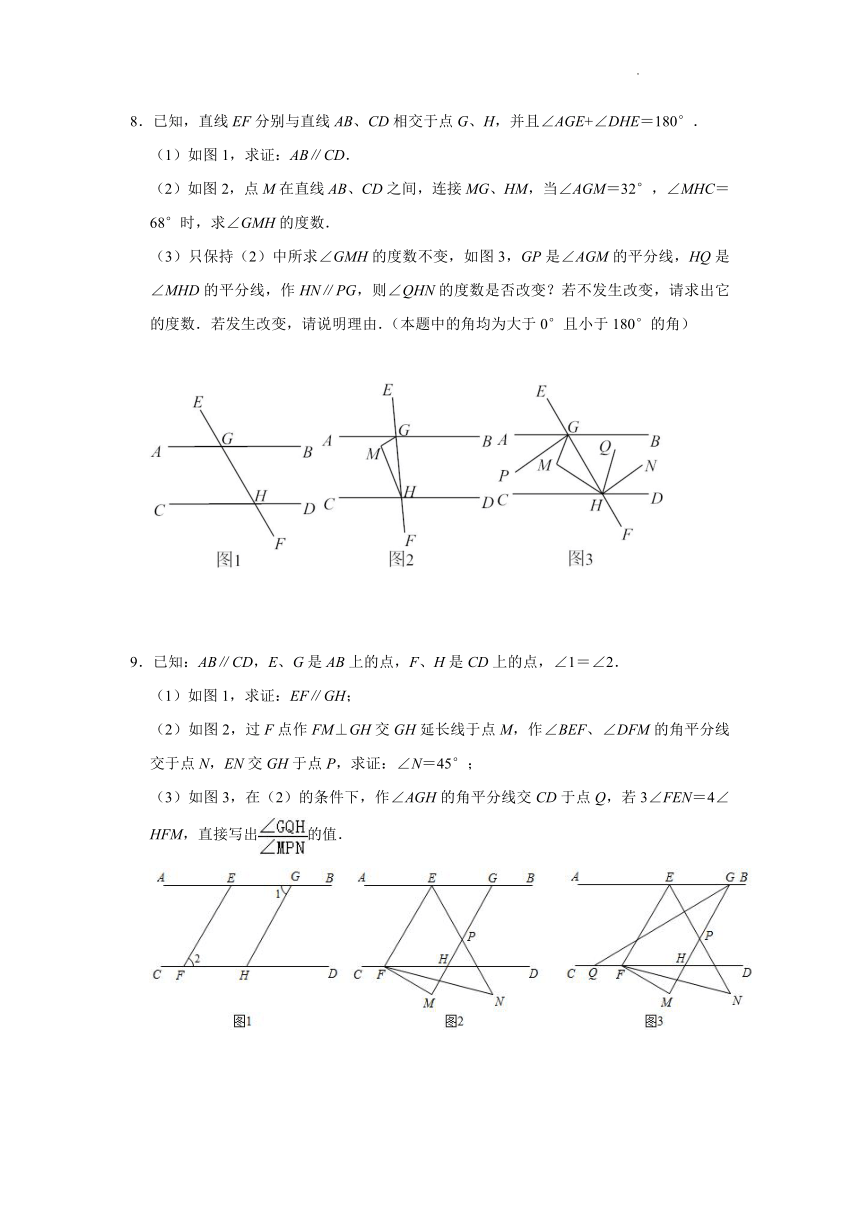
8.已知,直线EF分别与直线AB、CD相交于点G、H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD.
(2)如图2,点M在直线AB、CD之间,连接MG、HM,当∠AGM=32°,∠MHC=68°时,求∠GMH的度数.
(3)只保持(2)中所求∠GMH的度数不变,如图3,GP是∠AGM的平分线,HQ是∠MHD的平分线,作HN∥PG,则∠QHN的度数是否改变?若不发生改变,请求出它的度数.若发生改变,请说明理由.(本题中的角均为大于0°且小于180°的角)
9.已知:AB∥CD,E、G是AB上的点,F、H是CD上的点,∠1=∠2.
(1)如图1,求证:EF∥GH;
(2)如图2,过F点作FM⊥GH交GH延长线于点M,作∠BEF、∠DFM的角平分线交于点N,EN交GH于点P,求证:∠N=45°;
(3)如图3,在(2)的条件下,作∠AGH的角平分线交CD于点Q,若3∠FEN=4∠HFM,直接写出的值.
10.已知直线EF分别交直线AB、CD于点G、H,∠1+∠2=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,M、N分别为直线AB、CD上的点,P、Q为直线AB、CD之间不同的两点,∠PMQ=2∠BMQ,∠PNQ=2∠DNQ,∠MQN=30°.
①求证:PM⊥PN;
②如图3,∠EGB的平分线GL与∠MPN的邻补角∠MPT的平分线PL交于点L,∠PNH的平分线NK交EF于点K.若∠EKN+∠GLP=170°,直接写出∠PNH﹣∠EHD的大小.
11.如图,AD,BC相交于点O,∠MCD=∠BCM=α,∠B=4α.
(1)求证:AB∥CD;
(2)若∠A=∠B,求∠BOD的度数;(用含α的式子表示)
(3)若点E在AB上,连接OE,EP平分∠OEB交CM于点P,如备用图所示,求证:∠COE=2∠EPC+∠B.
12.[感知]如图①,AB∥CD,∠AEP=40°,∠PFD=130°,求∠EPF的度数.小明想到了以下方法:
解;(1)如图①,过点P作PM∥AB,
∴∠1=∠AEP=40°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠2+∠PFD=180°(两直线平行,同旁内角互补).
∵∠PFD=130°(已知),
∴∠2=180°﹣130°=50°(等式的性质),
∴∠1+∠2=40°+50°=90°(等式的性质).
即∠EPF=90°(等量代换).
[探究]如图②,AB∥CD,∠AEP=50°,∠PFC=120°,求∠EPF的度数.
[应用]如图③所示,在[探究]的条件下,∠PEA的平分线和∠PFC的平分线交于点G,则∠G的度数是 °.
13.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
14.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图1,求证:CF∥AB;
(2)如图2,连接BE,若∠ABE=40°,∠ACF=60°,求∠BEC的度数;
(3)如图3,在(2)的条件下,点G是线段FC延长线上一点,若∠EBC:∠ECB=7:13,BE平分∠ABG,求∠CBG的度数.
15.已知:如图,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图①所示,求证:OB∥AC.(注意证明过程要写依据)
(2)如图②,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.
(ⅰ)求∠EOC的度数;
(ⅱ)求∠OCB:∠OFB的比值;
(ⅲ)如图③,若∠OEB=∠OCA.此时∠OCA度数等于 .(在横线上填上答案即可)
16.(1)如图1,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在线段AB上,则∠1,∠2,∠3之间的等量关系是 ;如图2,点A在B处北偏东40°方向,在C处的北偏西45°方向,则∠BAC= °.
(2)如图3,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°,试说明:AB∥CD;并探究∠2与∠3的数量关系.
17.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC度数.
小明的思路是:过P作PE∥AB,如图2,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为 ;请说明理由;
问题迁移:
(2)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β,则∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
18.如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°.
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?
(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?
(2、3小题只需选一题说明理由)
19.如图1,CE平分∠ACD,AE平分∠BAC,且∠EAC+∠ACE=90°.
(1)请判断AB与CD的位置关系,并说明理由;
(2)如图2,当∠E=90°且AB与CD的位置关系保持不变,当直角顶点E点移动时,写出∠BAE与∠ECD的数量关系,并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点,且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外),∠CPQ+∠CQP与∠BAC有何数量关系?写出结论,并加以证明.
20.如图1,点A、B分别在直线GH、MN上,∠GAC=∠NBD,∠C=∠D.
(1)求证:GH∥MN;
(2)如图2,AE平分∠GAC,DE平分∠BDC,若∠AED=∠GAC,求∠GAC与∠ACD之间的数量关系;
(3)在(2)的条件下,如图3,BF平分∠DBM,点K在射线BF上,∠KAG=∠GAC,若∠AKB=∠ACD,直接写出∠GAC的度数 .
参考答案
1.解:∠1=∠2,
理由是:
∵∠ABC+∠ECB=180°,
∴AB∥CD,
∴∠ABC=∠BCD,
∵∠P=∠Q,
∴∠PBC=∠QCB,
∴∠ABC﹣∠PBC=∠BCD﹣∠QCB,
即∠1=∠2.
2.解:(1)∵BE平分∠ABC,
∴∠ABC=2∠ABE,
∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF;
(2)AF与BE的位置关系是垂直,理由如下:
∵∠ADE=∠BCD.
∴AD∥BC,
∴∠DAB+∠CBA=180°,
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABC=2∠ABE,∠BAD=2∠BAF,
∴2∠ABE+2∠BAF=180°,
∴∠ABE+∠BAF=90°,
∴∠AOB=90°,
∴AF⊥BE.
3.解:①猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴CD∥EF,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+∠CDP=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②猜想∠BPD=∠B+∠D
理由:过点P作EP∥AB,
∴∠B=∠BPE(两直线平行,同位角相等)
∵AB∥CD,EF∥AB,
∴CD∥EF,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD=∠D
∴∠BPD=∠B+∠D
③与②的作法相同,过点P作EP∥AB,可得:(3)∠BPD+∠B=∠D,(4)∠BPD=∠B﹣∠D
4.解:(1)过点A作ED∥BC,
∴∠B=∠EAB,∠C=∠DCA,
又∵∠EAB+∠BAC+∠DAC=180°,
∴∠B+∠BAC+∠C=180°.
(2)过点C作CF∥AB,
∵AB∥ED,
∴AB∥ED∥CF,
∴∠B=∠BCF,∠C=∠DCF,
∴∠B+∠BCD+∠D=∠BCF+∠BCD+∠DCF=360°.
(3)如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=60°,∠ADC=70°,
∴∠ABE=∠ABC=30°,∠CDE=∠ADC=35°,
∴∠BED=∠BEF+∠DEF=30°+35°=65°
故答案为:65;
5.解:(1)如图1,作EF∥AB,,
∵AB∥CD,
∴∠B=∠1,
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠D=∠2,
∴∠B+∠D=∠1+∠2,
又∵∠1+∠2=∠E,
∴∠B+∠D=∠E.
(2)如图2,作EF∥AB,,
∵EF∥AB,
∴∠B=∠1,
∵∠E=∠1+∠2=∠B+∠D,
∴∠D=∠2,
∴EF∥CD,
又∵EF∥AB,
∴AB∥CD.
(3)如图3,过E作EF∥AB,,
∵EF∥AB,
∴∠BEF+∠B=180°,
∵EF∥CD,
∴∠D+∠DEF=180°,
∵∠BEF+∠DEF=∠E,
∴∠E+∠B+∠D=180°+180°=360°.
(4)如图4,,
∵AB∥CD,
∴∠B=∠BFD,
∵∠D+∠E=∠BFD,
∴∠D+∠E=∠B.
(5)如图5,作EM∥AB,FN∥AB,GP∥AB,,
又∵AB∥CD,
∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,
∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;
∵∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,
∴∠E+∠G=∠B+∠F+∠D.
6.解:(1)证明:过P作PM∥AB,
∴∠A=∠APM,(两直线平行,内错角相等),
∵PM∥AB,AB∥CD(已知),
∴PM∥CD,(平行于同一直线的两直线平行),
∴∠C=∠CPM( 两直线平行,内错角相等),
∵∠APC=∠APM+∠CPM,
∴∠APC=∠A+∠C(等量代换),
故答案为:两直线平行,内错角相等,平行于同一直线的两直线平行,∠CPM,两直线平行,内错角相等;
(2)∠A+∠P+∠Q+∠C=540°,
故答案为:540°;
(3)m=x+z﹣y,
理由是:如图③,过P作PM∥AB,过Q作QN∥AB,
∵AB∥CD,
∴AB∥PM∥QN∥CD,
∴∠ABP=∠BPM=x,∠C=∠CQN,∠QPM=∠PQN,
∴∠C=∠CPQ﹣∠NPQ=∠CPQ﹣∠QPM=∠CQP﹣(∠BPQ﹣∠B)=z﹣(y﹣x)=x+z﹣y.
7.解:(1)∠PEQ=∠APE+∠CQE,
如图1,过点E作EH∥AB,则EH∥AB∥CD,
∵AB∥EH,
∴∠APE=∠PEH,
又∵CD∥EH,
∴∠CQE=∠HEQ,
∵∠PEQ=∠PEH+HEQ,
∴∠PEQ=∠APE+∠CQE;
(2)如图2,由(1)得,∠PEQ=∠APE+∠CQE=130°;
∵∠APE+∠BPE=180°,∠CQE+∠DQE=180°,
∴∠BPE+∠DQE=360°﹣130°=230°,
又∵PF平分∠BPE,QF平分∠EQD,
∴∠1=∠2,∠3=∠4,
∴∠1+∠3=(∠BPE+∠DQE)=×230°=115°,
在四边形PEQF中,
∠PFQ=360°﹣(∠1+∠2+∠PEQ)=360°﹣(115°+130°)=115°;
(3)140°,如图3,延长PF交CD与点M,
∵PF平分∠BPE,QH平分∠EQD,
∴∠1=∠2,∠3=∠4,
∵AB∥CD,
∴∠BPE=∠DNE,∠2=∠PMC=∠1,
又∵∠DQE=∠DNE+∠E,即2∠4=2∠1+80°,
∴∠4﹣∠1=40°,
∴∠PFQ=∠FQD+∠PMC=180°﹣∠4+∠1=180°﹣(∠4﹣∠1)=180°﹣40°=140°.
8.(1)证明:∵∠AGE+∠BGE=180°,∠AGE+∠DHE=180°,
∴∠BGE=∠DHE,
∴AB∥CD.
(2)解:∵AB∥CD,
∴∠AGH+∠CHG=180°,即∠AGM+∠MGH+∠MHG+∠MHC=180°,
∵∠MGH+∠MHG+∠GMH=180°,
∴∠GMH=∠AGM+∠MHC,
∵∠AGM=32°,∠MHC=68°,
∴∠GMH=100°.
(3)解:∠QHN的度数不发生改变,理由如下,
由(2)得,∠AGM+∠MHC=∠GMH=100°,
∴∠MGH+∠MHG=80°,
∵GP、HQ分别平分∠MGA和∠MHD,
∴∠MGP=∠MGA,∠MHQ=∠MHD=(180°﹣∠MHC)=90°﹣∠MHC,
∴∠PGH=∠MGP+∠MGH=∠MGA+∠MGH,
∵HN∥PG,
∴∠GHN=∠PGH=∠MGA+∠MGH,
∴∠QHN=∠GHN﹣∠GHQ=(∠MGA+∠MGH)﹣(∠MHQ﹣∠MHG)=∠MGA+∠MGH﹣∠MHQ+∠MHG=∠MGA+80°﹣∠MHQ,
∴∠QHN=∠MGA+80°﹣(90°﹣∠MHC)=﹣10°+(∠MGA+∠MHC)=﹣10°+×100°=40°.
9.解:(1)证明:∵AB∥CD,
∴∠2=∠3,
又∵∠1=∠2,
∴∠1=∠3,
∴EF∥GH;
(2)如图2,过点N作NK∥CD,
∴∠KNE=∠4,∠6=∠7,
设∠4=x,∠7=y,
∵EN、FN分别平分∠BEF、∠DFM,
∴∠ENK=∠5=∠4=x,∠6=∠8=∠7=y,
又∵AB∥CD,
∴∠EFD=180°﹣2x,
又∵FM⊥GH,
∴∠EFM=90°,
∴180°﹣2x+2y=90°,
∴x﹣y=45°,
∴∠ENF=∠ENK﹣∠6=x﹣y=45°,
(3)
∵3∠FEN=4∠HFM,即3x=4×2y,
∴x=,
∴x﹣y=﹣y=45°
∴y=27°,x=72°,
又∵EN和GQ是角平分线,
∴GQ⊥EN,
∴∠GQH=∠EGQ=180°﹣90°﹣72°=18°,
又∵∠MPN=∠FEN=x=72°,
∴,
故答案为.
10.证明:(1)∵∠1=∠HGB,∠1+∠2=180°,
∴∠HGB+∠2=180°,
∴AB∥CD,
(2)①过Q作QK∥AB,如图1,
∵AB∥CD,
∴QK∥AB∥CD,
∴∠BMQ=∠MQK,∠DNQ=∠KQN,
∴∠MQN=∠MQK+∠KQN=∠BMQ+∠DNQ,
同理,∠MPN=∠BMP+∠DNP,
设∠BMQ=x,∠DNQ=y,
则∠MQK=x,∠KQN=y,∠PMQ=2x,∠PNQ=2y,
∵∠MQN=30°,
∴x+y=30°,
∴∠MPN=3x+3y=90°,
∴PM⊥PN;
解:(2)②如图2,过L作IS∥AB,过P作PW′∥AB,过K作KW∥AB,
∵AB∥CD,
∴SI∥AB∥CD∥KW∥PW′,
∵GL平分∠EGB,
∴可设∠EGL=∠LGB=x,
同理,∠MPL=∠TPL=45°,可设∠CNK=∠KNP=y,
∵IS∥AB∥PW′,
∴∠ILG=∠LGB=x,
∠SLP=∠LPW′,
∵PW′∥CD,
∴∠W′PN=180°﹣∠CNP=180°﹣2y,
∴∠W′PL=180°﹣∠W′PN﹣∠LPT=2y﹣45°,
∴∠SLP=∠LPW′=2y﹣45°,
∴∠GLP=180°﹣∠ILG﹣∠SLP=225°﹣x﹣2y,
∵AB∥KW∥CD,
∴∠AGK=∠GKW=∠EGB=2x,∠WKN=∠KNC=y,
∴∠EKN=∠GKW+∠WKN=2x+y,
∵∠EKN+∠GLP=170°,
∴2x+y+225°﹣x﹣2y=170°,
∴y﹣x=55°,
∴∠PNH﹣∠EHD=2y﹣2x=110°.
11.证明:(1)∵∠MCD=∠BCM=α,
∴∠BCM=3α,
∴∠BCD=∠BCM+∠MCD=4α=∠B,
∴AB∥CD.
解:(2)过O做OF,使OF∥AB∥CD
∵AB∥CD,
∴∠D=∠A=∠B=3α,
∵AB∥OF,
∴∠B=∠BOF,
CD∥OF,
∴∠FOD=∠D,
∠BOD=∠BOF+∠FOD=∠B+∠D=4α+3α=7α.
证明:(3)过点P作AB、CD的平行线PQ,
∵AB∥PQ∥CD,
∴∠QPC=∠PCD=α,
∴∠BEP=∠EPQ=∠OEB,
∵∠COE=∠OEP+∠ENO,
且∠ENO=∠B+∠BEN=∠BNP,
∴∠COE=∠B+∠BEN+∠OEP=∠B+∠OEB,
又∵EP平分∠OEB,
∴∠COE=2∠EPC+∠B.
12.[探究]如图②,过点P作PM∥AB,
∴∠MPE=∠AEP=50°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠PFC=∠MPF=120°(两直线平行,内错角相等).
∴∠EPF=∠MPF﹣∠MPE=120°﹣50°=70°(等式的性质).
[应用]如图③所示,
∵EG是∠PEA的平分线,FG是∠PFC的平分线,
∴∠AEG=AEP=25°,∠GFC=PFC=60°,
过点G作GM∥AB,
∴∠MGE=∠AEG=25°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴GM∥CD(平行于同一条直线的两直线平行),
∴∠GFC=∠MGF=60°(两直线平行,内错角相等).
∴∠G=∠MGF﹣∠MGE=60°﹣25°=35°.
故答案为:35.
13.(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠GMH=∠GMR+∠RMH=∠AGM+∠CHM.
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点H作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CHG=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CHG=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
14.(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵∠BCF+∠ADE=180°.
∴∠BCF+∠B=180°.
∴CF∥AB;
(2)解:如图2,过点E作EK∥AB,
∴∠BEK=∠ABE=40°,
∵CF∥AB,
∴CF∥EK,
∴∠CEK=∠ACF=60°,
∴∠BEC=∠BEK+∠CEK=40°+60°=100°;
(3)∵BE平分∠ABG,
∴∠EBG=∠ABE=40°,
∵∠EBC:∠ECB=7:13,
∴设∠EBC=7x°,则∠ECB=13x°,
∵DE∥BC,
∴∠DEB=∠EBC=7x°,∠AED=∠ECB=13x°,
∵∠AED+∠DEB+∠BEC=180°,
∴13x+7x+100=180,
解得x=4,
∴∠EBC=7x°=28°,
∵∠EBG=∠EBC+∠CBG,
∴∠CBG=∠EBG﹣∠EBC=40°﹣28°=12°.
15.解:(1)∵BC∥OA,
∴∠B+∠O=180°,(两直线平行,同旁内角互补)
∵∠A=∠B,
∴∠A+∠O=180°,(等量代换)
∴OB∥AC.(同旁内角互补,两直线平行)
(2)(ⅰ)∵∠A=∠B=100°,
由(1)得∠BOA=180°﹣∠B=80°;
∵∠FOC=∠AOC,并且OE平分∠BOF,
∴∠EOF=∠BOF,∠FOC=∠FOA,
∴∠EOC=∠EOF+∠FOC=(∠BOF+∠FOA)=∠BOA=40°.
(ⅱ)∵BC∥OA,
∴∠FCO=∠COA,
又∵∠FOC=∠AOC,
∴∠FOC=∠FCO,
∴∠OFB=∠FOC+∠FCO=2∠OCB,
∴∠OCB:∠OFB=1:2.
(ⅲ)∵OB∥AC,
∴∠OCA=∠BOC,
设∠BOE=∠EOF=α,∠FOC=∠COA=β,
∴∠OCA=∠BOC=2α+β,
∠OEB=∠EOC+∠ECO=α+β+β=α+2β,
∵∠OEB=∠OCA,
∴2α+β=α+2β,
∴α=β,
∵∠AOB=80°,
∴α=β=20°,
∴∠OCA=2α+β=40°+20°=60°.
故答案是:60°.
16.解:(1)如图1中,作PM∥AC,
∵AC∥BD,
∴PM∥BD,
∴∠1=∠CPM,∠2=∠MPD,
∴∠1+∠2=∠CPM+∠MPD=∠CPD=∠3.
由题可知:∠BAC=∠B+∠C,
∵∠B=40°,∠C=45°,
∴∠BAC=40°+45°=85°.
故答案为:∠1+∠2=∠3,85°.
(2)证明:∵BE、DE平分∠ABD、∠BDC,
∴∠1=∠ABD,∠2=∠BDC;
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°;
∴AB∥CD;(同旁内角互补,两直线平行)
∵DE平分∠BDC,
∴∠2=∠FDE;
∵∠1+∠2=90°,
∴∠BED=∠DEF=90°;
∴∠3+∠FDE=90°;
∴∠2+∠3=90°.
17.解:(1)过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
故答案为110°.
(2)∠CPD=∠α+∠β,
理由是:如图3,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(3)当P在BA延长线时,
∠CPD=∠β﹣∠α;
当P在AB延长线时,
∠CPD=∠α﹣∠β.
18.解:(1)∵CE平分∠ACD,AE平分∠BAC,
∴∠BAC=2∠EAC,∠ACD=2∠ACE,
∵∠EAC+∠ACE=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAE+∠MCD=90°;
过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BAE=∠AEF,∠FEC=∠DCE,
∵∠E=90°,
∴∠BAE+∠ECD=90°,
∵∠MCE=∠ECD,
∴∠BAE+∠MCD=90°;
(3)∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠QPC+∠PQC+∠PCQ=180°,
∴∠BAC=∠PQC+∠QPC.
19.解:(1)AB∥CD,
理由:∵CE平分∠ACD,AE平分∠BAC,
∴∠ACD=2∠ACE,∠BAC=2∠EAC,
又∵∠EAC+∠ACE=90°,
∴∠ACD+∠BAC=180°,
∴AB∥CD;
(2)∠BAE+∠ECD=90°,
理由:延长AE交CD于点F,
∵AB∥CD,
∴∠BAE=∠AFC,
∵∠AEC是△EFC的一个外角,
∴∠AEC=∠AFC+∠ECD=90°,
∴∠BAE+∠ECD=90°;
(3)∠CPQ+∠CQP=∠BAC,
证明:∵AB∥CD,
∴∠BAC=∠ACG,
∵∠ACG是△PCQ的一个外角,
∴∠ACG=∠CPQ+∠CQP,
∴∠CPQ+∠CQP=∠BAC.
20.解:(1)如图1,延长AC交MN于点P,
∵∠ACD=∠D,
∴AP∥BD,
∴∠NBD=∠NPA,
∵∠GAC=∠NBD,
∴∠GAC=∠NPA,
∴GH∥MN;
(2)延长AC交MN于点P,交DE于点Q,
∵∠E+∠EAQ+∠AQE=180°,∠EQA+∠AQD=180°,
∴∠AQD=∠E+∠EAQ,
∵AC∥BD,
∴∠AQD=∠BDQ,
∴∠BDQ=∠E+∠EAQ,
∵AE平分∠GAC,DE平分∠BDC,
∴∠GAC=2∠EAQ,∠CDB=2∠BDQ,
∴∠CDB=2∠E+∠GAC,
∵∠AED=∠GAC,∠ACD=∠CDB,
∴∠ACD=2∠GAC+∠GAC=3∠GAC;
(3)当K在直线GH下方时,设射线BF交GH于I,
∵GH∥MN,
∴∠AIB=∠FBM,
∵BF平分∠MBD,
∴∠DBF=∠FBM=,
∴∠AIB=∠DBF,
∵∠AIB+∠KAG=∠AKB,∠AKB=∠ACD,
∴∠ACD=∠DBF+∠KAG,
∵∠KAG=∠GAC,∠GAC=∠NBD,
∴∠GAC+=∠ACD=3∠GAC,
即∠GAC+∠GAC=3∠GAC,
解得∠GAC=.
当K在直线GH上方时,同法可得∠GAC=()°.
故答案为或()°
1.如图,已知∠ABC+∠ECB=180°,∠P=∠Q,则∠1与∠2是否相等?说说你的理由.
2.如图,BE平分∠ABC交CD的延长线于E,∠ABC=2∠E,∠ADE=∠BCD.
(1)请说明AB∥EF的理由;
(2)若AF平分∠BAD交DC的延长线于F,判断AF与BE的位置关系,并说明理由.
3.如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说明理由.
(提示:三角形的内角和等于180°)
①填空或填写理由
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°
∵AB∥CD,EF∥AB,
∴ ∥ ,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+ =180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
③观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B、∠D的关系,不说明理由.
4.课题学行线的“等角转化”功能.
阅读理解:
如图1,已知点A是BC外一点,连接AB,AC.求∠BAC+∠B+∠C的度数.
(1)阅读并补充下面推理过程.
解:过点A作ED∥BC,所以∠B= ,∠C= .
又因为∠EAB+∠BAC+∠DAC=180°.所以∠B+∠BAC+∠C=180°.
解题反思:
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
方法运用:
(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.
提示:过点C作CF∥AB.
深化拓展:
(3)已知AB∥CD,点C在点D的右侧,∠ADC=70°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.
如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为 °.
5.(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?
(3)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(4)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?
6.(1)请在横线上填写合适的内容,完成下面的证明:
如图①,如果AB∥CD,求证:∠APC=∠A+∠C.
证明:过P作PM∥AB.
∴∠A=∠APM,( )
∵PM∥AB,AB∥CD(已知)
∴PM∥CD,( )
∴∠C= ( )
∵∠APC=∠APM+∠CPM,
∴∠APC=∠A+∠C(等量代换)
(2)如图②,AB∥CD,直接写出∠A+∠P+∠Q+∠C= .
(3)如图③,AB∥CD,若∠ABP=x,∠BPQ=y,∠PQC=z,∠QCD=m,你能用x,y,z表示m的大小吗?试说明理由.
7.某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论运用很广,请你利用这个结论解决以下问题:
已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.
(1)如图1,运用上述结论,探究∠PEQ与∠APE+∠CQE之间的数量关系.并说明理由;
(2)如图2,PF平分∠BPE,QF平分∠EQD,当∠PEQ=130°时,求出∠PFQ的度数;
(3)如图3,若点E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延长线交PF于点F,当∠PEQ=80°时,请直接写出∠PFQ的度数.
8.已知,直线EF分别与直线AB、CD相交于点G、H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD.
(2)如图2,点M在直线AB、CD之间,连接MG、HM,当∠AGM=32°,∠MHC=68°时,求∠GMH的度数.
(3)只保持(2)中所求∠GMH的度数不变,如图3,GP是∠AGM的平分线,HQ是∠MHD的平分线,作HN∥PG,则∠QHN的度数是否改变?若不发生改变,请求出它的度数.若发生改变,请说明理由.(本题中的角均为大于0°且小于180°的角)
9.已知:AB∥CD,E、G是AB上的点,F、H是CD上的点,∠1=∠2.
(1)如图1,求证:EF∥GH;
(2)如图2,过F点作FM⊥GH交GH延长线于点M,作∠BEF、∠DFM的角平分线交于点N,EN交GH于点P,求证:∠N=45°;
(3)如图3,在(2)的条件下,作∠AGH的角平分线交CD于点Q,若3∠FEN=4∠HFM,直接写出的值.
10.已知直线EF分别交直线AB、CD于点G、H,∠1+∠2=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,M、N分别为直线AB、CD上的点,P、Q为直线AB、CD之间不同的两点,∠PMQ=2∠BMQ,∠PNQ=2∠DNQ,∠MQN=30°.
①求证:PM⊥PN;
②如图3,∠EGB的平分线GL与∠MPN的邻补角∠MPT的平分线PL交于点L,∠PNH的平分线NK交EF于点K.若∠EKN+∠GLP=170°,直接写出∠PNH﹣∠EHD的大小.
11.如图,AD,BC相交于点O,∠MCD=∠BCM=α,∠B=4α.
(1)求证:AB∥CD;
(2)若∠A=∠B,求∠BOD的度数;(用含α的式子表示)
(3)若点E在AB上,连接OE,EP平分∠OEB交CM于点P,如备用图所示,求证:∠COE=2∠EPC+∠B.
12.[感知]如图①,AB∥CD,∠AEP=40°,∠PFD=130°,求∠EPF的度数.小明想到了以下方法:
解;(1)如图①,过点P作PM∥AB,
∴∠1=∠AEP=40°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠2+∠PFD=180°(两直线平行,同旁内角互补).
∵∠PFD=130°(已知),
∴∠2=180°﹣130°=50°(等式的性质),
∴∠1+∠2=40°+50°=90°(等式的性质).
即∠EPF=90°(等量代换).
[探究]如图②,AB∥CD,∠AEP=50°,∠PFC=120°,求∠EPF的度数.
[应用]如图③所示,在[探究]的条件下,∠PEA的平分线和∠PFC的平分线交于点G,则∠G的度数是 °.
13.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
14.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图1,求证:CF∥AB;
(2)如图2,连接BE,若∠ABE=40°,∠ACF=60°,求∠BEC的度数;
(3)如图3,在(2)的条件下,点G是线段FC延长线上一点,若∠EBC:∠ECB=7:13,BE平分∠ABG,求∠CBG的度数.
15.已知:如图,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图①所示,求证:OB∥AC.(注意证明过程要写依据)
(2)如图②,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.
(ⅰ)求∠EOC的度数;
(ⅱ)求∠OCB:∠OFB的比值;
(ⅲ)如图③,若∠OEB=∠OCA.此时∠OCA度数等于 .(在横线上填上答案即可)
16.(1)如图1,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在线段AB上,则∠1,∠2,∠3之间的等量关系是 ;如图2,点A在B处北偏东40°方向,在C处的北偏西45°方向,则∠BAC= °.
(2)如图3,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°,试说明:AB∥CD;并探究∠2与∠3的数量关系.
17.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC度数.
小明的思路是:过P作PE∥AB,如图2,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为 ;请说明理由;
问题迁移:
(2)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β,则∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
18.如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°.
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?
(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?
(2、3小题只需选一题说明理由)
19.如图1,CE平分∠ACD,AE平分∠BAC,且∠EAC+∠ACE=90°.
(1)请判断AB与CD的位置关系,并说明理由;
(2)如图2,当∠E=90°且AB与CD的位置关系保持不变,当直角顶点E点移动时,写出∠BAE与∠ECD的数量关系,并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点,且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外),∠CPQ+∠CQP与∠BAC有何数量关系?写出结论,并加以证明.
20.如图1,点A、B分别在直线GH、MN上,∠GAC=∠NBD,∠C=∠D.
(1)求证:GH∥MN;
(2)如图2,AE平分∠GAC,DE平分∠BDC,若∠AED=∠GAC,求∠GAC与∠ACD之间的数量关系;
(3)在(2)的条件下,如图3,BF平分∠DBM,点K在射线BF上,∠KAG=∠GAC,若∠AKB=∠ACD,直接写出∠GAC的度数 .
参考答案
1.解:∠1=∠2,
理由是:
∵∠ABC+∠ECB=180°,
∴AB∥CD,
∴∠ABC=∠BCD,
∵∠P=∠Q,
∴∠PBC=∠QCB,
∴∠ABC﹣∠PBC=∠BCD﹣∠QCB,
即∠1=∠2.
2.解:(1)∵BE平分∠ABC,
∴∠ABC=2∠ABE,
∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF;
(2)AF与BE的位置关系是垂直,理由如下:
∵∠ADE=∠BCD.
∴AD∥BC,
∴∠DAB+∠CBA=180°,
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABC=2∠ABE,∠BAD=2∠BAF,
∴2∠ABE+2∠BAF=180°,
∴∠ABE+∠BAF=90°,
∴∠AOB=90°,
∴AF⊥BE.
3.解:①猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴CD∥EF,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+∠CDP=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②猜想∠BPD=∠B+∠D
理由:过点P作EP∥AB,
∴∠B=∠BPE(两直线平行,同位角相等)
∵AB∥CD,EF∥AB,
∴CD∥EF,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD=∠D
∴∠BPD=∠B+∠D
③与②的作法相同,过点P作EP∥AB,可得:(3)∠BPD+∠B=∠D,(4)∠BPD=∠B﹣∠D
4.解:(1)过点A作ED∥BC,
∴∠B=∠EAB,∠C=∠DCA,
又∵∠EAB+∠BAC+∠DAC=180°,
∴∠B+∠BAC+∠C=180°.
(2)过点C作CF∥AB,
∵AB∥ED,
∴AB∥ED∥CF,
∴∠B=∠BCF,∠C=∠DCF,
∴∠B+∠BCD+∠D=∠BCF+∠BCD+∠DCF=360°.
(3)如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=60°,∠ADC=70°,
∴∠ABE=∠ABC=30°,∠CDE=∠ADC=35°,
∴∠BED=∠BEF+∠DEF=30°+35°=65°
故答案为:65;
5.解:(1)如图1,作EF∥AB,,
∵AB∥CD,
∴∠B=∠1,
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠D=∠2,
∴∠B+∠D=∠1+∠2,
又∵∠1+∠2=∠E,
∴∠B+∠D=∠E.
(2)如图2,作EF∥AB,,
∵EF∥AB,
∴∠B=∠1,
∵∠E=∠1+∠2=∠B+∠D,
∴∠D=∠2,
∴EF∥CD,
又∵EF∥AB,
∴AB∥CD.
(3)如图3,过E作EF∥AB,,
∵EF∥AB,
∴∠BEF+∠B=180°,
∵EF∥CD,
∴∠D+∠DEF=180°,
∵∠BEF+∠DEF=∠E,
∴∠E+∠B+∠D=180°+180°=360°.
(4)如图4,,
∵AB∥CD,
∴∠B=∠BFD,
∵∠D+∠E=∠BFD,
∴∠D+∠E=∠B.
(5)如图5,作EM∥AB,FN∥AB,GP∥AB,,
又∵AB∥CD,
∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D,
∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D;
∵∠1+∠2=∠E,∠5+∠6=∠G,∠3+∠4=∠F,
∴∠E+∠G=∠B+∠F+∠D.
6.解:(1)证明:过P作PM∥AB,
∴∠A=∠APM,(两直线平行,内错角相等),
∵PM∥AB,AB∥CD(已知),
∴PM∥CD,(平行于同一直线的两直线平行),
∴∠C=∠CPM( 两直线平行,内错角相等),
∵∠APC=∠APM+∠CPM,
∴∠APC=∠A+∠C(等量代换),
故答案为:两直线平行,内错角相等,平行于同一直线的两直线平行,∠CPM,两直线平行,内错角相等;
(2)∠A+∠P+∠Q+∠C=540°,
故答案为:540°;
(3)m=x+z﹣y,
理由是:如图③,过P作PM∥AB,过Q作QN∥AB,
∵AB∥CD,
∴AB∥PM∥QN∥CD,
∴∠ABP=∠BPM=x,∠C=∠CQN,∠QPM=∠PQN,
∴∠C=∠CPQ﹣∠NPQ=∠CPQ﹣∠QPM=∠CQP﹣(∠BPQ﹣∠B)=z﹣(y﹣x)=x+z﹣y.
7.解:(1)∠PEQ=∠APE+∠CQE,
如图1,过点E作EH∥AB,则EH∥AB∥CD,
∵AB∥EH,
∴∠APE=∠PEH,
又∵CD∥EH,
∴∠CQE=∠HEQ,
∵∠PEQ=∠PEH+HEQ,
∴∠PEQ=∠APE+∠CQE;
(2)如图2,由(1)得,∠PEQ=∠APE+∠CQE=130°;
∵∠APE+∠BPE=180°,∠CQE+∠DQE=180°,
∴∠BPE+∠DQE=360°﹣130°=230°,
又∵PF平分∠BPE,QF平分∠EQD,
∴∠1=∠2,∠3=∠4,
∴∠1+∠3=(∠BPE+∠DQE)=×230°=115°,
在四边形PEQF中,
∠PFQ=360°﹣(∠1+∠2+∠PEQ)=360°﹣(115°+130°)=115°;
(3)140°,如图3,延长PF交CD与点M,
∵PF平分∠BPE,QH平分∠EQD,
∴∠1=∠2,∠3=∠4,
∵AB∥CD,
∴∠BPE=∠DNE,∠2=∠PMC=∠1,
又∵∠DQE=∠DNE+∠E,即2∠4=2∠1+80°,
∴∠4﹣∠1=40°,
∴∠PFQ=∠FQD+∠PMC=180°﹣∠4+∠1=180°﹣(∠4﹣∠1)=180°﹣40°=140°.
8.(1)证明:∵∠AGE+∠BGE=180°,∠AGE+∠DHE=180°,
∴∠BGE=∠DHE,
∴AB∥CD.
(2)解:∵AB∥CD,
∴∠AGH+∠CHG=180°,即∠AGM+∠MGH+∠MHG+∠MHC=180°,
∵∠MGH+∠MHG+∠GMH=180°,
∴∠GMH=∠AGM+∠MHC,
∵∠AGM=32°,∠MHC=68°,
∴∠GMH=100°.
(3)解:∠QHN的度数不发生改变,理由如下,
由(2)得,∠AGM+∠MHC=∠GMH=100°,
∴∠MGH+∠MHG=80°,
∵GP、HQ分别平分∠MGA和∠MHD,
∴∠MGP=∠MGA,∠MHQ=∠MHD=(180°﹣∠MHC)=90°﹣∠MHC,
∴∠PGH=∠MGP+∠MGH=∠MGA+∠MGH,
∵HN∥PG,
∴∠GHN=∠PGH=∠MGA+∠MGH,
∴∠QHN=∠GHN﹣∠GHQ=(∠MGA+∠MGH)﹣(∠MHQ﹣∠MHG)=∠MGA+∠MGH﹣∠MHQ+∠MHG=∠MGA+80°﹣∠MHQ,
∴∠QHN=∠MGA+80°﹣(90°﹣∠MHC)=﹣10°+(∠MGA+∠MHC)=﹣10°+×100°=40°.
9.解:(1)证明:∵AB∥CD,
∴∠2=∠3,
又∵∠1=∠2,
∴∠1=∠3,
∴EF∥GH;
(2)如图2,过点N作NK∥CD,
∴∠KNE=∠4,∠6=∠7,
设∠4=x,∠7=y,
∵EN、FN分别平分∠BEF、∠DFM,
∴∠ENK=∠5=∠4=x,∠6=∠8=∠7=y,
又∵AB∥CD,
∴∠EFD=180°﹣2x,
又∵FM⊥GH,
∴∠EFM=90°,
∴180°﹣2x+2y=90°,
∴x﹣y=45°,
∴∠ENF=∠ENK﹣∠6=x﹣y=45°,
(3)
∵3∠FEN=4∠HFM,即3x=4×2y,
∴x=,
∴x﹣y=﹣y=45°
∴y=27°,x=72°,
又∵EN和GQ是角平分线,
∴GQ⊥EN,
∴∠GQH=∠EGQ=180°﹣90°﹣72°=18°,
又∵∠MPN=∠FEN=x=72°,
∴,
故答案为.
10.证明:(1)∵∠1=∠HGB,∠1+∠2=180°,
∴∠HGB+∠2=180°,
∴AB∥CD,
(2)①过Q作QK∥AB,如图1,
∵AB∥CD,
∴QK∥AB∥CD,
∴∠BMQ=∠MQK,∠DNQ=∠KQN,
∴∠MQN=∠MQK+∠KQN=∠BMQ+∠DNQ,
同理,∠MPN=∠BMP+∠DNP,
设∠BMQ=x,∠DNQ=y,
则∠MQK=x,∠KQN=y,∠PMQ=2x,∠PNQ=2y,
∵∠MQN=30°,
∴x+y=30°,
∴∠MPN=3x+3y=90°,
∴PM⊥PN;
解:(2)②如图2,过L作IS∥AB,过P作PW′∥AB,过K作KW∥AB,
∵AB∥CD,
∴SI∥AB∥CD∥KW∥PW′,
∵GL平分∠EGB,
∴可设∠EGL=∠LGB=x,
同理,∠MPL=∠TPL=45°,可设∠CNK=∠KNP=y,
∵IS∥AB∥PW′,
∴∠ILG=∠LGB=x,
∠SLP=∠LPW′,
∵PW′∥CD,
∴∠W′PN=180°﹣∠CNP=180°﹣2y,
∴∠W′PL=180°﹣∠W′PN﹣∠LPT=2y﹣45°,
∴∠SLP=∠LPW′=2y﹣45°,
∴∠GLP=180°﹣∠ILG﹣∠SLP=225°﹣x﹣2y,
∵AB∥KW∥CD,
∴∠AGK=∠GKW=∠EGB=2x,∠WKN=∠KNC=y,
∴∠EKN=∠GKW+∠WKN=2x+y,
∵∠EKN+∠GLP=170°,
∴2x+y+225°﹣x﹣2y=170°,
∴y﹣x=55°,
∴∠PNH﹣∠EHD=2y﹣2x=110°.
11.证明:(1)∵∠MCD=∠BCM=α,
∴∠BCM=3α,
∴∠BCD=∠BCM+∠MCD=4α=∠B,
∴AB∥CD.
解:(2)过O做OF,使OF∥AB∥CD
∵AB∥CD,
∴∠D=∠A=∠B=3α,
∵AB∥OF,
∴∠B=∠BOF,
CD∥OF,
∴∠FOD=∠D,
∠BOD=∠BOF+∠FOD=∠B+∠D=4α+3α=7α.
证明:(3)过点P作AB、CD的平行线PQ,
∵AB∥PQ∥CD,
∴∠QPC=∠PCD=α,
∴∠BEP=∠EPQ=∠OEB,
∵∠COE=∠OEP+∠ENO,
且∠ENO=∠B+∠BEN=∠BNP,
∴∠COE=∠B+∠BEN+∠OEP=∠B+∠OEB,
又∵EP平分∠OEB,
∴∠COE=2∠EPC+∠B.
12.[探究]如图②,过点P作PM∥AB,
∴∠MPE=∠AEP=50°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠PFC=∠MPF=120°(两直线平行,内错角相等).
∴∠EPF=∠MPF﹣∠MPE=120°﹣50°=70°(等式的性质).
[应用]如图③所示,
∵EG是∠PEA的平分线,FG是∠PFC的平分线,
∴∠AEG=AEP=25°,∠GFC=PFC=60°,
过点G作GM∥AB,
∴∠MGE=∠AEG=25°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴GM∥CD(平行于同一条直线的两直线平行),
∴∠GFC=∠MGF=60°(两直线平行,内错角相等).
∴∠G=∠MGF﹣∠MGE=60°﹣25°=35°.
故答案为:35.
13.(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠GMH=∠GMR+∠RMH=∠AGM+∠CHM.
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点H作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CHG=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CHG=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
14.(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵∠BCF+∠ADE=180°.
∴∠BCF+∠B=180°.
∴CF∥AB;
(2)解:如图2,过点E作EK∥AB,
∴∠BEK=∠ABE=40°,
∵CF∥AB,
∴CF∥EK,
∴∠CEK=∠ACF=60°,
∴∠BEC=∠BEK+∠CEK=40°+60°=100°;
(3)∵BE平分∠ABG,
∴∠EBG=∠ABE=40°,
∵∠EBC:∠ECB=7:13,
∴设∠EBC=7x°,则∠ECB=13x°,
∵DE∥BC,
∴∠DEB=∠EBC=7x°,∠AED=∠ECB=13x°,
∵∠AED+∠DEB+∠BEC=180°,
∴13x+7x+100=180,
解得x=4,
∴∠EBC=7x°=28°,
∵∠EBG=∠EBC+∠CBG,
∴∠CBG=∠EBG﹣∠EBC=40°﹣28°=12°.
15.解:(1)∵BC∥OA,
∴∠B+∠O=180°,(两直线平行,同旁内角互补)
∵∠A=∠B,
∴∠A+∠O=180°,(等量代换)
∴OB∥AC.(同旁内角互补,两直线平行)
(2)(ⅰ)∵∠A=∠B=100°,
由(1)得∠BOA=180°﹣∠B=80°;
∵∠FOC=∠AOC,并且OE平分∠BOF,
∴∠EOF=∠BOF,∠FOC=∠FOA,
∴∠EOC=∠EOF+∠FOC=(∠BOF+∠FOA)=∠BOA=40°.
(ⅱ)∵BC∥OA,
∴∠FCO=∠COA,
又∵∠FOC=∠AOC,
∴∠FOC=∠FCO,
∴∠OFB=∠FOC+∠FCO=2∠OCB,
∴∠OCB:∠OFB=1:2.
(ⅲ)∵OB∥AC,
∴∠OCA=∠BOC,
设∠BOE=∠EOF=α,∠FOC=∠COA=β,
∴∠OCA=∠BOC=2α+β,
∠OEB=∠EOC+∠ECO=α+β+β=α+2β,
∵∠OEB=∠OCA,
∴2α+β=α+2β,
∴α=β,
∵∠AOB=80°,
∴α=β=20°,
∴∠OCA=2α+β=40°+20°=60°.
故答案是:60°.
16.解:(1)如图1中,作PM∥AC,
∵AC∥BD,
∴PM∥BD,
∴∠1=∠CPM,∠2=∠MPD,
∴∠1+∠2=∠CPM+∠MPD=∠CPD=∠3.
由题可知:∠BAC=∠B+∠C,
∵∠B=40°,∠C=45°,
∴∠BAC=40°+45°=85°.
故答案为:∠1+∠2=∠3,85°.
(2)证明:∵BE、DE平分∠ABD、∠BDC,
∴∠1=∠ABD,∠2=∠BDC;
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°;
∴AB∥CD;(同旁内角互补,两直线平行)
∵DE平分∠BDC,
∴∠2=∠FDE;
∵∠1+∠2=90°,
∴∠BED=∠DEF=90°;
∴∠3+∠FDE=90°;
∴∠2+∠3=90°.
17.解:(1)过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
故答案为110°.
(2)∠CPD=∠α+∠β,
理由是:如图3,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(3)当P在BA延长线时,
∠CPD=∠β﹣∠α;
当P在AB延长线时,
∠CPD=∠α﹣∠β.
18.解:(1)∵CE平分∠ACD,AE平分∠BAC,
∴∠BAC=2∠EAC,∠ACD=2∠ACE,
∵∠EAC+∠ACE=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAE+∠MCD=90°;
过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BAE=∠AEF,∠FEC=∠DCE,
∵∠E=90°,
∴∠BAE+∠ECD=90°,
∵∠MCE=∠ECD,
∴∠BAE+∠MCD=90°;
(3)∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠QPC+∠PQC+∠PCQ=180°,
∴∠BAC=∠PQC+∠QPC.
19.解:(1)AB∥CD,
理由:∵CE平分∠ACD,AE平分∠BAC,
∴∠ACD=2∠ACE,∠BAC=2∠EAC,
又∵∠EAC+∠ACE=90°,
∴∠ACD+∠BAC=180°,
∴AB∥CD;
(2)∠BAE+∠ECD=90°,
理由:延长AE交CD于点F,
∵AB∥CD,
∴∠BAE=∠AFC,
∵∠AEC是△EFC的一个外角,
∴∠AEC=∠AFC+∠ECD=90°,
∴∠BAE+∠ECD=90°;
(3)∠CPQ+∠CQP=∠BAC,
证明:∵AB∥CD,
∴∠BAC=∠ACG,
∵∠ACG是△PCQ的一个外角,
∴∠ACG=∠CPQ+∠CQP,
∴∠CPQ+∠CQP=∠BAC.
20.解:(1)如图1,延长AC交MN于点P,
∵∠ACD=∠D,
∴AP∥BD,
∴∠NBD=∠NPA,
∵∠GAC=∠NBD,
∴∠GAC=∠NPA,
∴GH∥MN;
(2)延长AC交MN于点P,交DE于点Q,
∵∠E+∠EAQ+∠AQE=180°,∠EQA+∠AQD=180°,
∴∠AQD=∠E+∠EAQ,
∵AC∥BD,
∴∠AQD=∠BDQ,
∴∠BDQ=∠E+∠EAQ,
∵AE平分∠GAC,DE平分∠BDC,
∴∠GAC=2∠EAQ,∠CDB=2∠BDQ,
∴∠CDB=2∠E+∠GAC,
∵∠AED=∠GAC,∠ACD=∠CDB,
∴∠ACD=2∠GAC+∠GAC=3∠GAC;
(3)当K在直线GH下方时,设射线BF交GH于I,
∵GH∥MN,
∴∠AIB=∠FBM,
∵BF平分∠MBD,
∴∠DBF=∠FBM=,
∴∠AIB=∠DBF,
∵∠AIB+∠KAG=∠AKB,∠AKB=∠ACD,
∴∠ACD=∠DBF+∠KAG,
∵∠KAG=∠GAC,∠GAC=∠NBD,
∴∠GAC+=∠ACD=3∠GAC,
即∠GAC+∠GAC=3∠GAC,
解得∠GAC=.
当K在直线GH上方时,同法可得∠GAC=()°.
故答案为或()°
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
