2021-2022学年湘教版八年级数学下册 2.6菱形同步自主达标测试题 (word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学下册 2.6菱形同步自主达标测试题 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 279.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 21:24:58 | ||
图片预览




文档简介
2021-2022学年湘教版八年级数学下册《2-6菱形》同步自主达标测试题(附答案)
一.选择题(共8小题,满分32分)
1.如图,在菱形ABCD中,添加一个条件不能证明△ABE≌△CDF的是( )
A.∠BAE=∠FCD B.∠BEA=∠DFC C.AE=CF D.BE=DF
2.菱形ABCD的边长为8,有一个内角为120°,则较长的对角线的长为( )
A. B.8 C. D.4
3.如图,菱形OABC的边OA在平面直角坐标系中的x轴上,∠AOC=60°,OA=4,则点C的坐标为( )
A. B. C. D.(2,2)
4.如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=12,BD=16,则菱形的高AE为( )
A.9.6 B.4.8 C.10 D.5
5.如图,在菱形ABCD中,∠DAB=45°,DE⊥BC于点E,交对角线AC于点P,过点P作PF⊥CD于点F.若△PDF的周长为8.则菱形ABCD的面积为( )
A.16 B.16 C.32 D.32
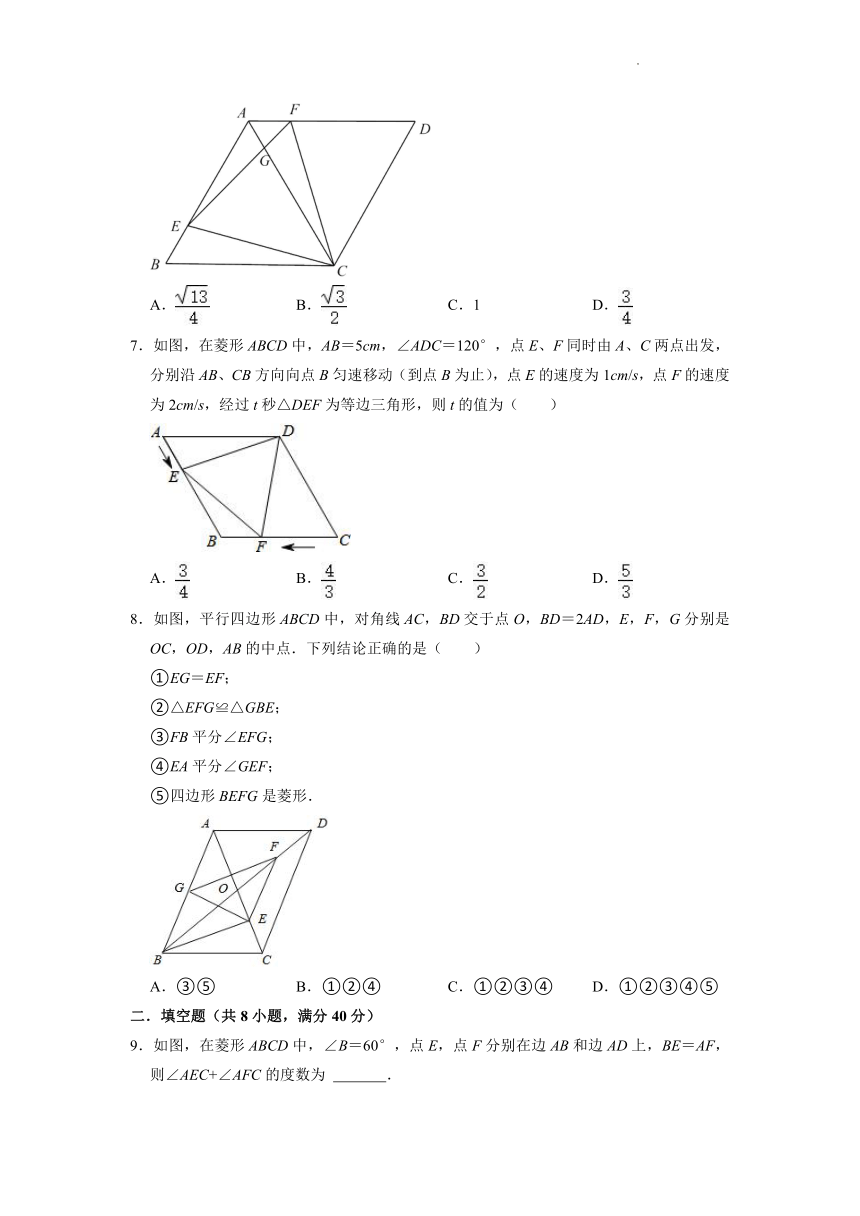
6.如图,菱形ABCD的边长为4,E、F分别是AB、AD.上的点,连接CE、CF、EF,AC与EF相交于点G,若BE=AF=1,∠BAD=120°,则FG的长为( )
A. B. C.1 D.
7.如图,在菱形ABCD中,AB=5cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
A. B. C. D.
8.如图,平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点.下列结论正确的是( )
①EG=EF;
②△EFG≌△GBE;
③FB平分∠EFG;
④EA平分∠GEF;
⑤四边形BEFG是菱形.
A.③⑤ B.①②④ C.①②③④ D.①②③④⑤
二.填空题(共8小题,满分40分)
9.如图,在菱形ABCD中,∠B=60°,点E,点F分别在边AB和边AD上,BE=AF,则∠AEC+∠AFC的度数为 .
10.菱形ABCD的面积为24,对角线AC的长为6,则对角线BD的长为 .
11.如图,四边形ABCD是边长为cm的菱形,其中对角线BD的长为2cm,则菱形ABCD的面积为 cm2.
12.已知菱形ABCD两条对角线的长分别为6和8,若另一个菱形EFGH的周长和面积分别是菱形ABCD周长和面积的2倍,则菱形EFGH两条对角线的长分别是 .
13.如图,菱形ABCD边长为4,∠B=60°,DE=AD,BF=BC,连接EF交菱形的对角线AC于点O,则图中阴影部分面积等于 .
14.在菱形ABCD中,对角线AC和BD相交于点O,OE为△BOC中BC边上的高.若△ABC的两条边长分别为8和6,则线段CE的长为 .
15.如图,在菱形ABCD外侧作等边△CBE,连接DE、AE.若∠ABC=100°,则∠DEA的大小为 .
16.如图,BD为边长为a的菱形ABCD的对角线,∠BAD=60°,点M,N分别从点A,B同时出发,以相同的速度沿AB,BD向终点B和D运动,连接DM和AN,DM和AN相交于点P,连接BP,则BP的最小值为 .
三.解答题(共7小题,满分48分)
17.如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF.
(1)求证:△ABE≌△CDF;
(2)连接BD,若∠1=32°,∠ADB=22°,请直接写出当∠ABE= °时,四边形BFDE是菱形.
18.已知,如图,四边形ABCD的对角线AC⊥BD于点E,点F为四边形ABCD外一点,且∠FCA=90°,BC平分∠DBF,∠CBF=∠DCB.求证:四边形DBFC是菱形.
19.已知:平行四边形ABCD,对角线AC,BD相交于点O.E是AD的中点,连接OE并延长至F使得OE=EF,连接FD,FC,FC交BD于点G.
求证:(1)△FGD≌△CGO;
(2)当AB与AC有怎样的数量关系时,四边形FOCD是菱形,并说明理由.
20.如图,在 ABCD中,对角线AC与BD相交于点O,过点O的直线EF与BA,DC的延长线分别交于点E,F,连接BF,DE.
(1)求证:AE=CF;
(2)请添加一个条件,使四边形BFDE是菱形,并说明理由.
21.如图,过 ABCD对角线AC与BD的交点E作两条互相垂直的直线,分别交边AB、BC、CD、DA于点P、M、Q、N.
(1)求证:△PBE≌△QDE;
(2)顺次连接点P,M,Q,N,求证:四边形PMQN是菱形.
22.如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
(1)求证:△ECG≌△GHD;
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论.
(3)若∠B=30°,判定四边形AEGF是否为菱形,并说明理由.
23.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,求OE的长.
参考答案
一.选择题(共8小题,满分32分)
1.解:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,∠ABE=∠CDF,
A、添加∠BAE=∠FCD,利用ASA能得出△ABE≌△CDF,不符合题意;
B、添加∠BEA=∠DFC,利用AAS能得出△ABE≌△CDF,不符合题意;
C、添加AE=CF,不能得出△ABE≌△CDF,符合题意;
D、添加BE=DF,利用SAS能得出△ABE≌△CDF,不符合题意;
故选:C.
2.解:在菱形ABCD中,∠BAO=∠BAD=×120°=60°,
又在△ABC中,AB=BC,
∴∠BCA=∠BAC=60°,
∠ABC=180°﹣∠BCA﹣∠BAC=60°,
∴△ABC为等边三角形,
∴AC=AB=8,
∴AO=4,
∴BO=,
∴BD=2BO=8,
故选:A.
3.解:过C作CD⊥OA于D,如图:
则∠ODC=90°,
∵四边形OABC是菱形,
∴OC=OA=4,
∵∠AOC=60°,
∴∠CDO=90°﹣∠AOC=30°,
∴DD=OC=2,
∴CD===2,
∴点C的坐标为(2,2),
故选:A.
4.解:在菱形ABCD中,AC=12,BD=16,
∴BO=BD=8,OC=AC=6,AC⊥BD,
∴BC===10,
∵AE⊥BC,
∴S菱形ABCD=AC BD=BC AE,
∴AE=×=9.6,
故选:A.
5.解:∵四边形ABCD是菱形,
∴BC=CD,∠BCD=∠BAD,∠ACB=∠ACD,AD∥BC,
∴∠BAD+∠B=180°,
∵∠DAB=45°,
∴∠BCD=∠BAD=45°,
∵DE⊥BC,
∴△CDE是等腰直角三角形,
∴∠CDE=45°,CD=DE,
∵PF⊥CD,
∴△DPF是等腰直角三角形,
∴PF=DF,PD=PF,
设PF=DF=x,则PD=x,
∵△PDF的周长为8,
∴x+x+x=8,
解得:x=8﹣4,
∵∠ACB=∠ACD,DE⊥BC,PF⊥CD,
∴PE=PF=x,
∴DE=x+x=(1+)×(8﹣4)=4,
∴BC=CD=DE=8,
∴菱形ABCD的面积=BC×DE=8×4=32,
故选:D.
6.解:过点E作EM∥BC交AC于M,EN⊥BC于N,如图所示:
∵菱形ABCD的边长为4,∠BAD=120°,
∴AB=BC=4,∠BAC=∠FAC=∠BAD=60°,AD∥BC,
∴△ABC是等边三角形,
∴∠B=∠ACB=60°,BC=AC,
∵EM∥BC,
∴EM∥AD,∠AEM=∠B=60°=∠BAC,
∴△AEM是等边三角形,
∴AM=AE=AB﹣BE=4﹣1=3,
∵EM∥AD,
∴FG=EF,
在△BCE和△ACF中,
,
∴△BCE≌△ACF(SAS),
∴CE=CF,∠BCE=∠ACF,
∴∠ACF+∠ACE=∠ACF+∠ACE=∠ACB=60°,
∴△CEF是等边三角形,
∴EF=CE,
∵EN⊥BC,∠B=60°,
∴∠BEN=30°,
∴BN=BE=,
∴EN=BN=,CN=BC﹣BN=4﹣=,
∴EF=CE===,
∴FG=EF=,
故选:A.
7.解:连接BD,
∵四边形ABCD是菱形,
∴AB=AD,∠ADB=∠ADC=60°,
∴△ABD是等边三角形,
∴AD=BD,
又∵△DEF是等边三角形,
∴∠EDF=∠DEF=60°,
又∵∠ADB=60°,
∴∠ADE=∠BDF,
在△ADE和△BDF中,,
∴△ADE≌△BDF(ASA),
∴AE=BF,
∵AE=t,CF=2t,
∴BF=BC﹣CF=5﹣2t,
∴t=5﹣2t
∴t=,
故选:D.
8.解:设GF和AC的交点为点P,如图:
∵E、F分别是OC、OD的中点,
∴EF∥CD,且EF=CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,且AB=CD,
∴∠FEG=∠BGE,
∵点G为AB的中点,
∴BG=AB=CD=FE,
在△EFG和△GBE中,,
∴△EFG≌△GBE(SAS),即②正确,
∴∠EGF=∠GEB,GF=BE,
∴GF∥BE,
∵BD=2BC,点O为平行四边形对角线交点,
∴BO=BD=BC,
∵E为OC中点,
∴BE⊥OC,
∴GP⊥AC,
∴∠APG=∠EPG=90°
∵GP∥BE,G为AB中点,
∴P为AE中点,即AP=PE,且GP=BE,
在△APG和△EGP中,,
∴△APG≌△EPG(SAS),
∴AG=EG=AB,
∴EG=EF,即①正确,
∵EF∥BG,GF∥BE,
∴四边形BGFE为平行四边形,
∴GF=BE,
∵GP=BE=GF,
∴GP=FP,
∵GF⊥AC,
∴∠GPE=∠FPE=90°
在△GPE和△FPE中,,
∴△GPE≌△FPE(SAS),
∴∠GEP=∠FEP,
∴EA平分∠GEF,即④正确.
∵BG=FE,GF=BE,
∴四边形BEFG是平行四边形,
没有条件得出BEFG是菱形,⑤③不正确;
故选:B.
二.填空题(共8小题,满分40分)
9.解:连接AC,如图所示:
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠D=∠B=60°,
∴△ABC是等边三角形,
∴AC=BC=CD,∠BAC=60°=∠D,
∵BE=AF,
∴AE=DF,
在△ACE和△DCF中,
,
∴△ACE≌△DCF(SAS),
∴∠AEC=∠DFC,
∵∠DFC+∠AFC=180°,
∴∠AEC+∠AFC=180°,
故答案为:180°.
10.解:菱形ABCD的面积S=AC BD=24,
∵AC=6,
∴BD==8,
故答案为8.
11.解:∵四边形ABCD是菱形,
∴BO=DO,AC⊥DB,AO=CO,
∵BD=2cm,
∴BO=1cm,
∵AB=cm,
∴AO===2(cm),
∴AC=2AO=4cm.
∴S菱形ABCD=(cm2).
故答案为:4.
12.解:如图,菱形ABCD中,AC=8,BD=6,
∴OA=AC=4,OB=BD=3,AC⊥BD,
∴AB==5,
∴菱形ABCD的周长是:5×4=20,面积是:×6×8=24.
∵另一个菱形EFGH的周长和面积分别是菱形ABCD周长和面积的2倍,
∴菱形EFGH的周长和面积分别是40,48,
∴菱形EFGH的边长是10,
设菱形EFGH的对角线为2a,2b,
∴a2+b2=100,×2a×2b=48,
∴a=﹣,b=+,
∴菱形EFGH两条对角线的长分别是2﹣2,2+2,
故答案为:2﹣2,2+2.
13.解:连接CE,
∵四边形ABCD是菱形,
∴AD=CD,AD∥BC,∠ABC=∠ADC=60°,
∴△ADC是等边三角形,∠DAC=∠ACB,
∴S△ADC=×AD2=4,
∵DE=AD,BF=BC,
∴AE=CF,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(AAS),
∴AO=CO,
∵DE=AD,
∴S△CDE=S△ADC=,S△ACE=3,
∵AO=CO,
∴S△AOE=S△COE=,
∴阴影部分面积=4﹣=,
故答案为:.
14.解:如图,
∵四边形ABCD是菱形,AC⊥BD,OE为△BOC中BC边上的高,
∴∠BOC=∠OBC=90°,
∵∠BCO=∠OCB,
①当对角线AC为8,菱形的边长BC为6时,
∵四边形ABCD是菱形,
∴OC=AC=4,
∴,
解得:CE=;
②当对角线AC为6,菱形的边长BC为8时,
∵四边形ABCD是菱形,
∴OC=AC=3,
∴,
解得:CE=,
故答案为:或.
15.解:∵四边形ABCD是菱形,
∴AB=BC=CD,AB∥CD,
∴∠BCD=180°﹣∠ABC=80°,
∵△CBE是等边三角形,
∴BC=BE=CE,∠CBE=∠BCE=∠BEC=60°,
∴AB=BE,CD=CE,∠DCE=140°,∠ABE=160°,
∴∠CED=∠CDE=(180°﹣∠DCE)=20°,∠BAE=∠BEA=(180°﹣160°)=10°,
∴∠DEA=∠BEC﹣∠DEC﹣∠BEA=30°,
故答案为:30°.
16.解:∵菱形ABCD中∠BAD=60°,
∴△ABD为等边三角形,AB=AD,
∴AB=AD=BD=a,∠DAM=∠ABN=60°,
∵点M和点N的时间和速度相同,
∴AM=BN,
∴△DAM≌△ABN(SAS),
∴∠ADM=∠BAN,
∵∠DAP+∠BAN=∠DAM=60°,
∴∠PDA+∠PAD=60°,
∴∠APD=120°,
延长CD至点E,使得ED=CD,连接AE,则△AED是等边三角形,
∴AE=ED=AD=a,∠EAD=∠EDA=∠AED=60°,
∴∠DEA+∠APD=180°,∠EAD+∠DAP+∠EDA+∠ADP=180°,
连接BO交⊙O于点P,此时BP最小,
过点O作OH⊥ED于点H,连接OD,则∠EOD=2∠EAD=120°,∠OHD=90°,DH=ED=a,
∴∠HDO=30°,
∴r=OD=,∠ODB=∠EDA+∠ADB﹣∠ODE=60°+60°﹣30°=90°,
∴OB===,
∴BP最小值=OB﹣r=﹣=,
故答案为:.
三.解答题(共7小题,满分48分)
17.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠BCD,
∴∠1=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:当∠ABE=12°时,四边形BFDE是菱形,理由如下:
∵△ABE≌△CDF,
∴BE=DF,AE=CF,
∴BF=DE,
∴四边形BFDE是平行四边形,
∵∠1=32°,∠ADB=22°,
∴∠ABD=∠1﹣∠ADB=10°,
∵∠ABE=12°,
∴∠DBE=∠ABD+∠ABE=22°,
∴∠DBE=∠ADB=22°,
∴BE=DE,
∴平行四边形BFDE是菱形,
故答案为:12.
18.证明:∵AC⊥BD,∠FCA=90°,
∴∠AEB=∠ACF,
∴BD∥CF,
∵∠CBF=∠DCB,
∴CD∥BF,
∴四边形DBFC是平行四边形,
∵BC平分∠DBF,
∴∠CBF=∠CBD,
∵∠CBF=∠DCB,
∴∠CBD=∠DCB,
∴CD=BD,
∴四边形DBFC是菱形.
19.(1)证明:在△ACD中,点O,E分别为边AC,AD中点,
∴OE为△ACD的中位线,
∴OE∥CD,,
又∵,
∴OF∥CD,OF=CD,
∴四边形OCDF为平行四边形,
∴FD∥OC,FD=OC,
∴∠GFD=∠GCO,∠GDF=∠GOC,
∴△FGD≌△HGO(ASA);
(2)解:当时,四边形FOCD是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,OC=AC,
∵AB=AC,
∴AB=CD=OC,
由(1)得:四边形OCDF为平行四边形,
∴平行四边形FOCD是菱形,
20.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,
∴∠AEO=∠CFO,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴AE=CF;
(2)解:添加一个条件:EF⊥BD,理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD,
由(1)点:△AOE≌△COF,
∴OE=OF,
∴四边形BFDE是平行四边形,
∵EF⊥BD,
∴四边形BFDE是菱形.
21.证明:(1)∵四边形ABCD是平行四边形,
∴EB=ED,AB∥CD,
∴∠EBP=∠EDQ,
在△PBE和△QDE中,
,
∴△PBE≌△QDE(ASA);
(2)如图所示:
由(1)得:△PBE≌△QDE,
∴EP=EQ,
同理:△BME≌△DNE(ASA),
∴EM=EN,
∴四边形PMQN是平行四边形,
∵PQ⊥MN,
∴平行四边形PMQN是菱形.
22.解:(1)∵AF=FG,
∴∠FAG=∠FGA,
∵AG平分∠CAB,
∴∠CAG=∠FAG,
∴∠CAG=∠FGA,
∴AC∥FG,
∵DE⊥AC,
∴FG⊥DE,
∵FG⊥BC,
∴DE∥BC,
∴AC⊥BC,
∴∠C=∠DHG=90°,∠CGE=∠GED,
∵F是AD的中点,FG∥AE,
∴H是ED的中点,
∴FG是线段ED的垂直平分线,
∴GE=GD,∠GDE=∠GED,
∵DE∥BC,
∴∠CGE=∠GED=∠GDE,
∴△ECG≌△GHD(AAS);
(2)证明:过点G作GP⊥AB于P,
∴GC=GP,而AG=AG,
∴△CAG≌△PAG,
∴AC=AP,
由(1)可得EG=DG,
∴Rt△ECG≌Rt△DPG,
∴EC=PD,
∴AD=AP+PD=AC+EC;
(3)四边形AEGF是菱形,
证明:∵∠B=30°,
∴∠ADE=30°,
∴AE=AD,
∴AE=AF=FG,
由(1)得AE∥FG,
∴四边形AEGF是平行四边形,
∴四边形AEGF是菱形.
23.(1)证明:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=BD=1,
在Rt△AOB中,AB=,OB=1,
∴OA==2,
∴OE=OA=2.
一.选择题(共8小题,满分32分)
1.如图,在菱形ABCD中,添加一个条件不能证明△ABE≌△CDF的是( )
A.∠BAE=∠FCD B.∠BEA=∠DFC C.AE=CF D.BE=DF
2.菱形ABCD的边长为8,有一个内角为120°,则较长的对角线的长为( )
A. B.8 C. D.4
3.如图,菱形OABC的边OA在平面直角坐标系中的x轴上,∠AOC=60°,OA=4,则点C的坐标为( )
A. B. C. D.(2,2)
4.如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=12,BD=16,则菱形的高AE为( )
A.9.6 B.4.8 C.10 D.5
5.如图,在菱形ABCD中,∠DAB=45°,DE⊥BC于点E,交对角线AC于点P,过点P作PF⊥CD于点F.若△PDF的周长为8.则菱形ABCD的面积为( )
A.16 B.16 C.32 D.32
6.如图,菱形ABCD的边长为4,E、F分别是AB、AD.上的点,连接CE、CF、EF,AC与EF相交于点G,若BE=AF=1,∠BAD=120°,则FG的长为( )
A. B. C.1 D.
7.如图,在菱形ABCD中,AB=5cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )
A. B. C. D.
8.如图,平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点.下列结论正确的是( )
①EG=EF;
②△EFG≌△GBE;
③FB平分∠EFG;
④EA平分∠GEF;
⑤四边形BEFG是菱形.
A.③⑤ B.①②④ C.①②③④ D.①②③④⑤
二.填空题(共8小题,满分40分)
9.如图,在菱形ABCD中,∠B=60°,点E,点F分别在边AB和边AD上,BE=AF,则∠AEC+∠AFC的度数为 .
10.菱形ABCD的面积为24,对角线AC的长为6,则对角线BD的长为 .
11.如图,四边形ABCD是边长为cm的菱形,其中对角线BD的长为2cm,则菱形ABCD的面积为 cm2.
12.已知菱形ABCD两条对角线的长分别为6和8,若另一个菱形EFGH的周长和面积分别是菱形ABCD周长和面积的2倍,则菱形EFGH两条对角线的长分别是 .
13.如图,菱形ABCD边长为4,∠B=60°,DE=AD,BF=BC,连接EF交菱形的对角线AC于点O,则图中阴影部分面积等于 .
14.在菱形ABCD中,对角线AC和BD相交于点O,OE为△BOC中BC边上的高.若△ABC的两条边长分别为8和6,则线段CE的长为 .
15.如图,在菱形ABCD外侧作等边△CBE,连接DE、AE.若∠ABC=100°,则∠DEA的大小为 .
16.如图,BD为边长为a的菱形ABCD的对角线,∠BAD=60°,点M,N分别从点A,B同时出发,以相同的速度沿AB,BD向终点B和D运动,连接DM和AN,DM和AN相交于点P,连接BP,则BP的最小值为 .
三.解答题(共7小题,满分48分)
17.如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF.
(1)求证:△ABE≌△CDF;
(2)连接BD,若∠1=32°,∠ADB=22°,请直接写出当∠ABE= °时,四边形BFDE是菱形.
18.已知,如图,四边形ABCD的对角线AC⊥BD于点E,点F为四边形ABCD外一点,且∠FCA=90°,BC平分∠DBF,∠CBF=∠DCB.求证:四边形DBFC是菱形.
19.已知:平行四边形ABCD,对角线AC,BD相交于点O.E是AD的中点,连接OE并延长至F使得OE=EF,连接FD,FC,FC交BD于点G.
求证:(1)△FGD≌△CGO;
(2)当AB与AC有怎样的数量关系时,四边形FOCD是菱形,并说明理由.
20.如图,在 ABCD中,对角线AC与BD相交于点O,过点O的直线EF与BA,DC的延长线分别交于点E,F,连接BF,DE.
(1)求证:AE=CF;
(2)请添加一个条件,使四边形BFDE是菱形,并说明理由.
21.如图,过 ABCD对角线AC与BD的交点E作两条互相垂直的直线,分别交边AB、BC、CD、DA于点P、M、Q、N.
(1)求证:△PBE≌△QDE;
(2)顺次连接点P,M,Q,N,求证:四边形PMQN是菱形.
22.如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
(1)求证:△ECG≌△GHD;
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论.
(3)若∠B=30°,判定四边形AEGF是否为菱形,并说明理由.
23.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,求OE的长.
参考答案
一.选择题(共8小题,满分32分)
1.解:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,∠ABE=∠CDF,
A、添加∠BAE=∠FCD,利用ASA能得出△ABE≌△CDF,不符合题意;
B、添加∠BEA=∠DFC,利用AAS能得出△ABE≌△CDF,不符合题意;
C、添加AE=CF,不能得出△ABE≌△CDF,符合题意;
D、添加BE=DF,利用SAS能得出△ABE≌△CDF,不符合题意;
故选:C.
2.解:在菱形ABCD中,∠BAO=∠BAD=×120°=60°,
又在△ABC中,AB=BC,
∴∠BCA=∠BAC=60°,
∠ABC=180°﹣∠BCA﹣∠BAC=60°,
∴△ABC为等边三角形,
∴AC=AB=8,
∴AO=4,
∴BO=,
∴BD=2BO=8,
故选:A.
3.解:过C作CD⊥OA于D,如图:
则∠ODC=90°,
∵四边形OABC是菱形,
∴OC=OA=4,
∵∠AOC=60°,
∴∠CDO=90°﹣∠AOC=30°,
∴DD=OC=2,
∴CD===2,
∴点C的坐标为(2,2),
故选:A.
4.解:在菱形ABCD中,AC=12,BD=16,
∴BO=BD=8,OC=AC=6,AC⊥BD,
∴BC===10,
∵AE⊥BC,
∴S菱形ABCD=AC BD=BC AE,
∴AE=×=9.6,
故选:A.
5.解:∵四边形ABCD是菱形,
∴BC=CD,∠BCD=∠BAD,∠ACB=∠ACD,AD∥BC,
∴∠BAD+∠B=180°,
∵∠DAB=45°,
∴∠BCD=∠BAD=45°,
∵DE⊥BC,
∴△CDE是等腰直角三角形,
∴∠CDE=45°,CD=DE,
∵PF⊥CD,
∴△DPF是等腰直角三角形,
∴PF=DF,PD=PF,
设PF=DF=x,则PD=x,
∵△PDF的周长为8,
∴x+x+x=8,
解得:x=8﹣4,
∵∠ACB=∠ACD,DE⊥BC,PF⊥CD,
∴PE=PF=x,
∴DE=x+x=(1+)×(8﹣4)=4,
∴BC=CD=DE=8,
∴菱形ABCD的面积=BC×DE=8×4=32,
故选:D.
6.解:过点E作EM∥BC交AC于M,EN⊥BC于N,如图所示:
∵菱形ABCD的边长为4,∠BAD=120°,
∴AB=BC=4,∠BAC=∠FAC=∠BAD=60°,AD∥BC,
∴△ABC是等边三角形,
∴∠B=∠ACB=60°,BC=AC,
∵EM∥BC,
∴EM∥AD,∠AEM=∠B=60°=∠BAC,
∴△AEM是等边三角形,
∴AM=AE=AB﹣BE=4﹣1=3,
∵EM∥AD,
∴FG=EF,
在△BCE和△ACF中,
,
∴△BCE≌△ACF(SAS),
∴CE=CF,∠BCE=∠ACF,
∴∠ACF+∠ACE=∠ACF+∠ACE=∠ACB=60°,
∴△CEF是等边三角形,
∴EF=CE,
∵EN⊥BC,∠B=60°,
∴∠BEN=30°,
∴BN=BE=,
∴EN=BN=,CN=BC﹣BN=4﹣=,
∴EF=CE===,
∴FG=EF=,
故选:A.
7.解:连接BD,
∵四边形ABCD是菱形,
∴AB=AD,∠ADB=∠ADC=60°,
∴△ABD是等边三角形,
∴AD=BD,
又∵△DEF是等边三角形,
∴∠EDF=∠DEF=60°,
又∵∠ADB=60°,
∴∠ADE=∠BDF,
在△ADE和△BDF中,,
∴△ADE≌△BDF(ASA),
∴AE=BF,
∵AE=t,CF=2t,
∴BF=BC﹣CF=5﹣2t,
∴t=5﹣2t
∴t=,
故选:D.
8.解:设GF和AC的交点为点P,如图:
∵E、F分别是OC、OD的中点,
∴EF∥CD,且EF=CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,且AB=CD,
∴∠FEG=∠BGE,
∵点G为AB的中点,
∴BG=AB=CD=FE,
在△EFG和△GBE中,,
∴△EFG≌△GBE(SAS),即②正确,
∴∠EGF=∠GEB,GF=BE,
∴GF∥BE,
∵BD=2BC,点O为平行四边形对角线交点,
∴BO=BD=BC,
∵E为OC中点,
∴BE⊥OC,
∴GP⊥AC,
∴∠APG=∠EPG=90°
∵GP∥BE,G为AB中点,
∴P为AE中点,即AP=PE,且GP=BE,
在△APG和△EGP中,,
∴△APG≌△EPG(SAS),
∴AG=EG=AB,
∴EG=EF,即①正确,
∵EF∥BG,GF∥BE,
∴四边形BGFE为平行四边形,
∴GF=BE,
∵GP=BE=GF,
∴GP=FP,
∵GF⊥AC,
∴∠GPE=∠FPE=90°
在△GPE和△FPE中,,
∴△GPE≌△FPE(SAS),
∴∠GEP=∠FEP,
∴EA平分∠GEF,即④正确.
∵BG=FE,GF=BE,
∴四边形BEFG是平行四边形,
没有条件得出BEFG是菱形,⑤③不正确;
故选:B.
二.填空题(共8小题,满分40分)
9.解:连接AC,如图所示:
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠D=∠B=60°,
∴△ABC是等边三角形,
∴AC=BC=CD,∠BAC=60°=∠D,
∵BE=AF,
∴AE=DF,
在△ACE和△DCF中,
,
∴△ACE≌△DCF(SAS),
∴∠AEC=∠DFC,
∵∠DFC+∠AFC=180°,
∴∠AEC+∠AFC=180°,
故答案为:180°.
10.解:菱形ABCD的面积S=AC BD=24,
∵AC=6,
∴BD==8,
故答案为8.
11.解:∵四边形ABCD是菱形,
∴BO=DO,AC⊥DB,AO=CO,
∵BD=2cm,
∴BO=1cm,
∵AB=cm,
∴AO===2(cm),
∴AC=2AO=4cm.
∴S菱形ABCD=(cm2).
故答案为:4.
12.解:如图,菱形ABCD中,AC=8,BD=6,
∴OA=AC=4,OB=BD=3,AC⊥BD,
∴AB==5,
∴菱形ABCD的周长是:5×4=20,面积是:×6×8=24.
∵另一个菱形EFGH的周长和面积分别是菱形ABCD周长和面积的2倍,
∴菱形EFGH的周长和面积分别是40,48,
∴菱形EFGH的边长是10,
设菱形EFGH的对角线为2a,2b,
∴a2+b2=100,×2a×2b=48,
∴a=﹣,b=+,
∴菱形EFGH两条对角线的长分别是2﹣2,2+2,
故答案为:2﹣2,2+2.
13.解:连接CE,
∵四边形ABCD是菱形,
∴AD=CD,AD∥BC,∠ABC=∠ADC=60°,
∴△ADC是等边三角形,∠DAC=∠ACB,
∴S△ADC=×AD2=4,
∵DE=AD,BF=BC,
∴AE=CF,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(AAS),
∴AO=CO,
∵DE=AD,
∴S△CDE=S△ADC=,S△ACE=3,
∵AO=CO,
∴S△AOE=S△COE=,
∴阴影部分面积=4﹣=,
故答案为:.
14.解:如图,
∵四边形ABCD是菱形,AC⊥BD,OE为△BOC中BC边上的高,
∴∠BOC=∠OBC=90°,
∵∠BCO=∠OCB,
①当对角线AC为8,菱形的边长BC为6时,
∵四边形ABCD是菱形,
∴OC=AC=4,
∴,
解得:CE=;
②当对角线AC为6,菱形的边长BC为8时,
∵四边形ABCD是菱形,
∴OC=AC=3,
∴,
解得:CE=,
故答案为:或.
15.解:∵四边形ABCD是菱形,
∴AB=BC=CD,AB∥CD,
∴∠BCD=180°﹣∠ABC=80°,
∵△CBE是等边三角形,
∴BC=BE=CE,∠CBE=∠BCE=∠BEC=60°,
∴AB=BE,CD=CE,∠DCE=140°,∠ABE=160°,
∴∠CED=∠CDE=(180°﹣∠DCE)=20°,∠BAE=∠BEA=(180°﹣160°)=10°,
∴∠DEA=∠BEC﹣∠DEC﹣∠BEA=30°,
故答案为:30°.
16.解:∵菱形ABCD中∠BAD=60°,
∴△ABD为等边三角形,AB=AD,
∴AB=AD=BD=a,∠DAM=∠ABN=60°,
∵点M和点N的时间和速度相同,
∴AM=BN,
∴△DAM≌△ABN(SAS),
∴∠ADM=∠BAN,
∵∠DAP+∠BAN=∠DAM=60°,
∴∠PDA+∠PAD=60°,
∴∠APD=120°,
延长CD至点E,使得ED=CD,连接AE,则△AED是等边三角形,
∴AE=ED=AD=a,∠EAD=∠EDA=∠AED=60°,
∴∠DEA+∠APD=180°,∠EAD+∠DAP+∠EDA+∠ADP=180°,
连接BO交⊙O于点P,此时BP最小,
过点O作OH⊥ED于点H,连接OD,则∠EOD=2∠EAD=120°,∠OHD=90°,DH=ED=a,
∴∠HDO=30°,
∴r=OD=,∠ODB=∠EDA+∠ADB﹣∠ODE=60°+60°﹣30°=90°,
∴OB===,
∴BP最小值=OB﹣r=﹣=,
故答案为:.
三.解答题(共7小题,满分48分)
17.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠BCD,
∴∠1=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:当∠ABE=12°时,四边形BFDE是菱形,理由如下:
∵△ABE≌△CDF,
∴BE=DF,AE=CF,
∴BF=DE,
∴四边形BFDE是平行四边形,
∵∠1=32°,∠ADB=22°,
∴∠ABD=∠1﹣∠ADB=10°,
∵∠ABE=12°,
∴∠DBE=∠ABD+∠ABE=22°,
∴∠DBE=∠ADB=22°,
∴BE=DE,
∴平行四边形BFDE是菱形,
故答案为:12.
18.证明:∵AC⊥BD,∠FCA=90°,
∴∠AEB=∠ACF,
∴BD∥CF,
∵∠CBF=∠DCB,
∴CD∥BF,
∴四边形DBFC是平行四边形,
∵BC平分∠DBF,
∴∠CBF=∠CBD,
∵∠CBF=∠DCB,
∴∠CBD=∠DCB,
∴CD=BD,
∴四边形DBFC是菱形.
19.(1)证明:在△ACD中,点O,E分别为边AC,AD中点,
∴OE为△ACD的中位线,
∴OE∥CD,,
又∵,
∴OF∥CD,OF=CD,
∴四边形OCDF为平行四边形,
∴FD∥OC,FD=OC,
∴∠GFD=∠GCO,∠GDF=∠GOC,
∴△FGD≌△HGO(ASA);
(2)解:当时,四边形FOCD是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,OC=AC,
∵AB=AC,
∴AB=CD=OC,
由(1)得:四边形OCDF为平行四边形,
∴平行四边形FOCD是菱形,
20.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,
∴∠AEO=∠CFO,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴AE=CF;
(2)解:添加一个条件:EF⊥BD,理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD,
由(1)点:△AOE≌△COF,
∴OE=OF,
∴四边形BFDE是平行四边形,
∵EF⊥BD,
∴四边形BFDE是菱形.
21.证明:(1)∵四边形ABCD是平行四边形,
∴EB=ED,AB∥CD,
∴∠EBP=∠EDQ,
在△PBE和△QDE中,
,
∴△PBE≌△QDE(ASA);
(2)如图所示:
由(1)得:△PBE≌△QDE,
∴EP=EQ,
同理:△BME≌△DNE(ASA),
∴EM=EN,
∴四边形PMQN是平行四边形,
∵PQ⊥MN,
∴平行四边形PMQN是菱形.
22.解:(1)∵AF=FG,
∴∠FAG=∠FGA,
∵AG平分∠CAB,
∴∠CAG=∠FAG,
∴∠CAG=∠FGA,
∴AC∥FG,
∵DE⊥AC,
∴FG⊥DE,
∵FG⊥BC,
∴DE∥BC,
∴AC⊥BC,
∴∠C=∠DHG=90°,∠CGE=∠GED,
∵F是AD的中点,FG∥AE,
∴H是ED的中点,
∴FG是线段ED的垂直平分线,
∴GE=GD,∠GDE=∠GED,
∵DE∥BC,
∴∠CGE=∠GED=∠GDE,
∴△ECG≌△GHD(AAS);
(2)证明:过点G作GP⊥AB于P,
∴GC=GP,而AG=AG,
∴△CAG≌△PAG,
∴AC=AP,
由(1)可得EG=DG,
∴Rt△ECG≌Rt△DPG,
∴EC=PD,
∴AD=AP+PD=AC+EC;
(3)四边形AEGF是菱形,
证明:∵∠B=30°,
∴∠ADE=30°,
∴AE=AD,
∴AE=AF=FG,
由(1)得AE∥FG,
∴四边形AEGF是平行四边形,
∴四边形AEGF是菱形.
23.(1)证明:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=BD=1,
在Rt△AOB中,AB=,OB=1,
∴OA==2,
∴OE=OA=2.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
