2021-2022学年北师大版八年级数学下册3.2图形的旋转同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册3.2图形的旋转同步练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 493.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 00:00:00 | ||
图片预览



文档简介
3.2图形的旋转 北师大版
一、单选题
1.下列道路交通标志图中,是中心对称图形的是( )
A. B. C.D.
2.下列图形中,是中心对称图形,但不是轴对称图形的是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
3.在平面直角坐标系中,已知,现将A点绕原点O顺时针旋转90°得到,则的坐标是( )
A. B. C. D.
4.如图,在△ABC中,AB=4,AC=3,∠BAC=30°,将△ABC绕点A按逆时针旋转60°得到△A1B1C1连接BC1,则BC1的长为( )
A.3 B.4 C.5 D.6
5.如图,将绕点顺时针旋转60°得到,若,则等于( )
A.2cm B.3cm C.4cm D.5cm
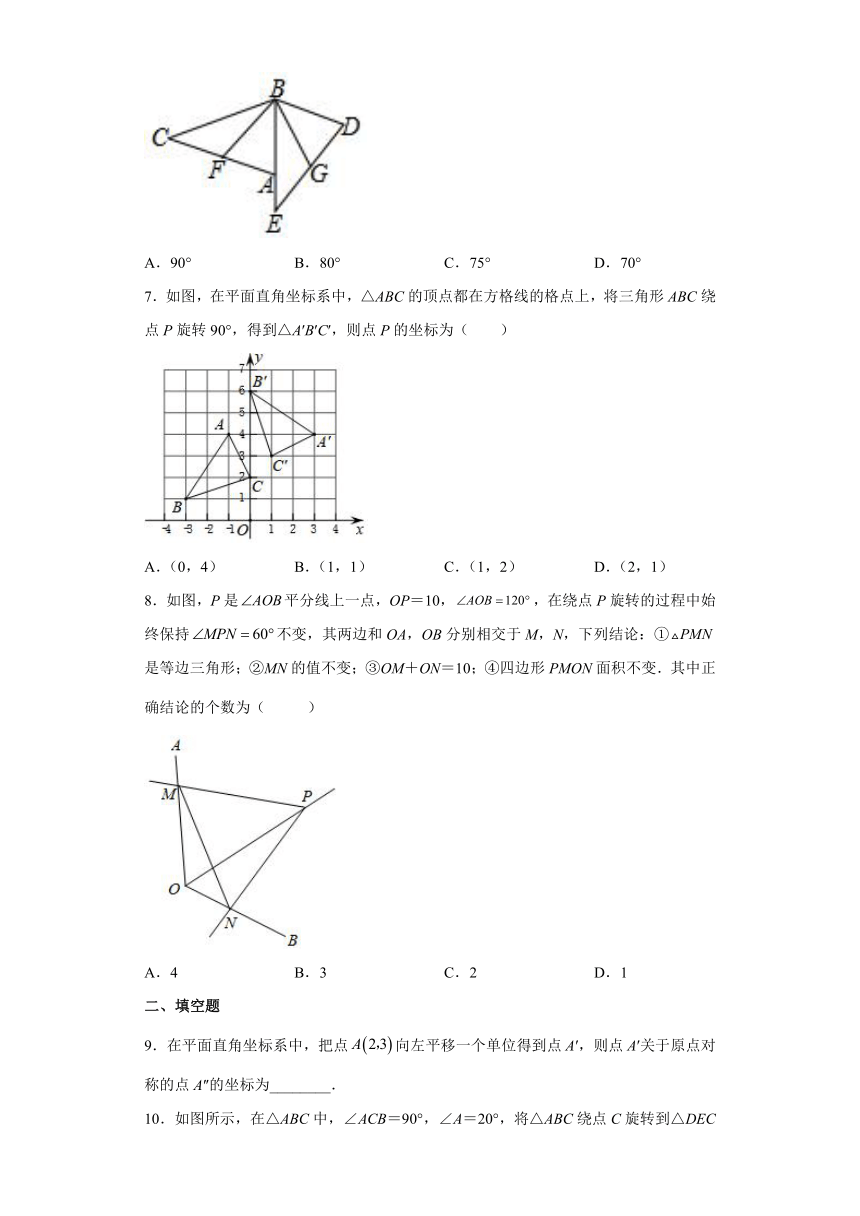
6.如图,在△ABC中,AC=BC,∠C=40°.将△ABC绕着点B逆时针方向旋转得△DBE,其中AC∥BD,BF、BG分别为△ABC与△DBE的中线,则∠FBG=( )
A.90° B.80° C.75° D.70°
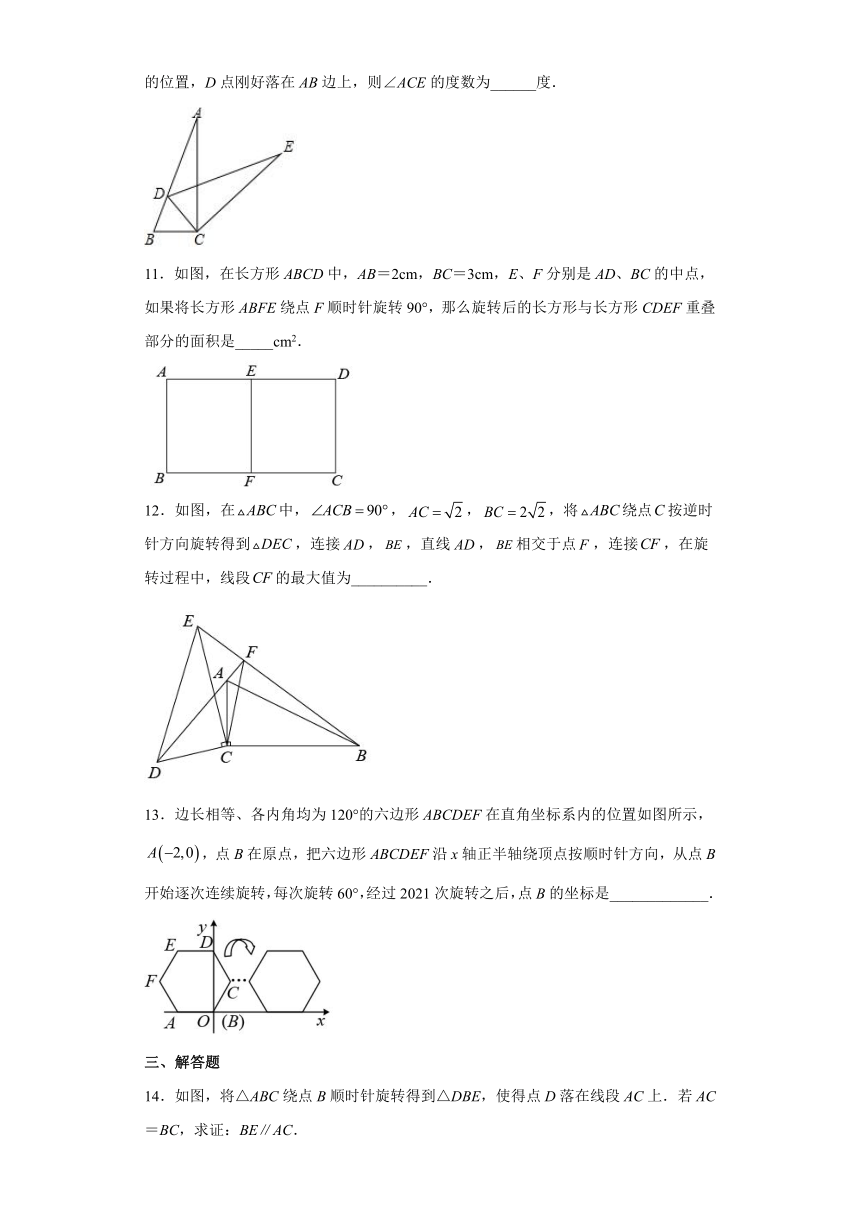
7.如图,在平面直角坐标系中,△ABC的顶点都在方格线的格点上,将三角形ABC绕点P旋转90°,得到△A′B′C′,则点P的坐标为( )
A.(0,4) B.(1,1) C.(1,2) D.(2,1)
8.如图,P是平分线上一点,OP=10,,在绕点P旋转的过程中始终保持不变,其两边和OA,OB分别相交于M,N,下列结论:①是等边三角形;②MN的值不变;③OM+ON=10;④四边形PMON面积不变.其中正确结论的个数为( )
A.4 B.3 C.2 D.1
二、填空题
9.在平面直角坐标系中,把点向左平移一个单位得到点A′,则点A′关于原点对称的点A″的坐标为________.
10.如图所示,在△ABC中,∠ACB=90°,∠A=20°,将△ABC绕点C旋转到△DEC的位置,D点刚好落在AB边上,则∠ACE的度数为______度.
11.如图,在长方形ABCD中,AB=2cm,BC=3cm,E、F分别是AD、BC的中点,如果将长方形ABFE绕点F顺时针旋转90°,那么旋转后的长方形与长方形CDEF重叠部分的面积是_____cm2.
12.如图,在中,,,,将绕点按逆时针方向旋转得到,连接,,直线,相交于点,连接,在旋转过程中,线段的最大值为__________.
13.边长相等、各内角均为120°的六边形ABCDEF在直角坐标系内的位置如图所示,,点B在原点,把六边形ABCDEF沿x轴正半轴绕顶点按顺时针方向,从点B开始逐次连续旋转,每次旋转60°,经过2021次旋转之后,点B的坐标是_____________.
三、解答题
14.如图,将△ABC绕点B顺时针旋转得到△DBE,使得点D落在线段AC上.若AC=BC,求证:BE∥AC.
15.如图,在平面直角坐标系xOy中,是由ABC平移得到,已知,,三点的坐标分别为,,,点A的坐标为.
(1)画出ABC.
(2)描述ABC到的平移过程.
(3)已知点P(0,b)为ABC内的一点,求点P在内的对应点的坐标.
16.如图,在Rt△ABC中,∠BAC=90°,∠ACB=30°,将△ABC绕点C逆时针旋转60°得到△CDE,点A、B的对应点分别是D、E,点F是边BC中点,连结AD、EF.
(1)求证:△ACD是等边三角形;
(2)判断AD与EF有怎样的数量关系,并说明理由.
17.在平面直角坐标系中,已知点,,连接AB,将AB向下平移5个单位得线段CD,其中点A的对应点为点C.
(1)填空:点C的坐标为______,线段AB平移到CD扫过的面积为______;
(2)若点P是y轴上的动点,连接PD.
①如图(1),当点P在y轴正半轴时,线段PD与线段AC相交于点E,用等式表示三角形PEC的面积与三角形ECD的面积之间的关系,并说明理由;
②当PD将四边形ACDB的面积分成2:3两部分时,求点P的坐标.
试卷第1页,共3页
参考答案:
1.C
【解析】
解:A、不是中心对称图形,本选项不符合题意;
B、不是中心对称图形,本选项不符合题意;
C、是中心对称图形,本选项符合题意;
D、不是中心对称图形,本选项不符合题意.
故选:C.
2.D
【解析】
解:A中正方形既是中心对称图形又是轴对称图形,不符合题意;
B中矩形既是中心对称图形又是轴对称图形,不符合题意;
C中菱形既是中心对称图形又是轴对称图形,不符合题意;
D平行四边形是中心对称图形但不是轴对称图形,符合题意;
故选D.
3.B
【解析】
解:,现将A点绕原点O顺时针旋转90°得到,则的坐标是
故选B
4.C
【解析】
解:由旋转的定义和性质可得AC1=AC=3,∠B1AC1=∠BAC=30°,∠BAB1=60°.
∴∠BAC1=90°.
∴在Rt△BAC1中,利用勾股定理可得BC1==5.
故选:C.
5.B
【解析】
解:∵△ABC绕点A顺时针旋转60°得到△AED,
∴AB=AE,∠BAE=60°,
∴△AEB是等边三角形,
∴BE=AB,
∵AB=3cm,
∴BE=3cm.
故选:B.
6.D
【解析】
解:,
,
,
,
由旋转可知,点绕点旋转后的对应点分别为点,
,
故选:D.
7.C
【解析】
解:选两组对应点,连接后作其中垂线,两中垂线的交点即为点P,由图知,旋转中心P的坐标为(1,2)
故选:C.
8.B
【解析】
如图作PE⊥OA于E,PF⊥OB于F.
∵∠PEO=∠PFO=90°,
∴∠EPF+∠AOB=180°,
∵∠MPN+∠AOB=180°,
∴∠EPF=∠MPN,
∴∠EPM=∠FPN,
∵OP平分∠AOB,PE⊥OA于E,PF⊥OB于F,
∴PE=PF,
在Rt△POE和Rt△POF中,
,
∴Rt△POE≌Rt△POF(HL),
∴OE=OF,
在△PEM和△PFN中,
,
∴△PEM≌△PFN(ASA),
∴EM=NF,PM=PN,S△PEM=S△PNF,
∵
∴是等边三角形,故①正确;
∵S△PEM=S△PNF,
∴S四边形PMON=S四边形PEOF=定值,故④正确;
∵OM+ON=OE+ME+OF-NF=2OE=10,故③正确;
∵M,N的位置变化,
∴MN的长度是变化的,故②错误;
故选:B.
9.(-1,-3)
【解析】
根据平移方式可知点的坐标为(1,3),
∴点关于原点对称的点的坐标为(-1,-3).
故答案为:(-1,-3).
10.40
【解析】
解:∵∠ACB=90°,∠A=20°,
∴∠B=70°;
由题意得:BC=DC,
∴∠CDB=∠B=70°,
∴∠BCD=180°-40°,
∴∠ACE=∠BCD=40°.
故答案为:40
11.2.25
【解析】
解:如图,将长方形ABFE绕点F顺时针旋转90度,得到长方形A′B′FE′,设A′B′与DC交于点G,
则FC=FB=FB′=BC=1.5cm,
所以旋转后的长方形A′B′FE′与长方形CDEF重叠部分B′FCG是正方形,边长为1.5cm,
所以,面积S=1.5×1.5=2.25(cm2).
故答案是:2.25.
12.
【解析】
解:取AB的中点H,连接CH、FH,设EC,DF交于点G,
在△ABC中,∠ACB=90 ,
∵AC=,BC=2,
∴AB=,
由旋转可知:△DCE≌△ACB,
∴∠DCE=∠ACB,DC=AC,CE=CB,
∴∠DCA=∠BCE,
∵∠ADC=(180 -∠ACD) ,∠BEC= (180 -∠BCE),
∴∠ADC=∠BEC,
∵∠DGC=∠EGF,
∴∠DCG=∠EFG=90 ,
∴∠AFB=90 ,
∵H是AB的中点,
∴FH=AB,
∵∠ACB=90 ,
∴CH=AB,
∴FH=CH=AB=,
在△FCH中,FH+CH>CF,
当F、C、H在一条直线上时,CF有最大值,
∴线段CF的最大值为.
故答案为:
13.
【解析】
∵正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,
∴每6次翻转为一个循环组循环,
∵,
∴经过2021次翻转为第337循环组的第5次翻转,点B在开始时点C的位置,
∵,
∴,
∴翻转前进的距离为:,
如图,过点B作BG⊥x于G,
则∠BAG=60°,
∴,
,
∴,
∴点B的坐标为.
故答案为:.
14.证明见解析.
【解析】
证明:,
,
由旋转的性质得:,,
,
,
.
15.(1)见解析
(2)向下平移3个单位长度
(3)
【解析】
(1)
解:根据题意可得:,,得出点A到向下移动三个单位长度,
∴,,
依次连接各点,作图如下:
(2)
解:根据图形及坐标可得:向下平移3个单位长度得;
(3)
解:∵由(2)可得:向下平移3个单位长度得,点P的坐标为,
∴根据平移的性质得对应点P的坐标为.
16.(1)见解析过程;
(2)AD=EF,理由见解析过程.
【解析】
(1)
证明:∵将△ABC绕点C逆时针旋转60°得到△CDE,
∴AC=CD,∠ACD=60°,
∴△ACD是等边三角形;
(2)
解:AD=EF,理由如下:
∵将△ABC绕点C逆时针旋转60°得到△CDE,
∴∠BCE=60°,BC=CE,
∵△ACD是等边三角形,
∴AD=AC,
∵点F是边BC中点,
∴BC=2CF,
∵∠BAC=90°,∠ACB=30°,
∴BC=2AB,∠ABC=60°=∠BCE,
∴AB=CF,
在△ABC和△DEC中,
,
∴△ABC≌△FCE(SAS),
∴EF=AC,
∴AD=EF.
17.(1)
(2)①S△PEC=S△ECD,理由见解析;②点P坐标为(0,5)或(0,).
【解析】
(1)
解:将AB向下平移5个单位得线段CD,
线段AB平移到CD扫过的面积为:
故答案为:
(2)
①如图1,过P点作PF⊥AC于F,
由平移知,轴,
∵A(2,4),
∴PF=2,
由平移知,CD=AB=4,
∴S△PEC=CE PF=CE×2=CE,S△ECD=CE CD=CE×4=2CE,
∴S△ECD=2S△PEC,
即:S△PEC=S△ECD;
②(ⅰ)如图2,当PD交线段AC于E,且PD将四边形ACDB分成面积为2:3两部分时,
连接PC,延长DC交y轴于点M,则M(0,﹣1),
∴OM=1,
连接AC,则S△ACD=S长方形ABDC=10,
∵PD将四边形ACDB的面积分成2:3两部分,
∴S△CDE=S矩形ABDC=×20=8,
由①知,S△PEC=S△ECD=×8=4,
∴S△PCD=S△PEC+S△ECD=4+8=12,
∵S△PCD=CD PM=×4PM=12,
∴PM=6,
∴PO=PM﹣OM=6﹣1=5,
∴P(0,5).
(ⅱ)如图3,当PD交AB于点F,PD将四边形ACDB分成面积为2:3两部分时,
连接PB,延长BA交y轴于点G,则G(0,4),
∴OG=4,连接AC,则S△ABD=S长方形ABDC=10,
∵PD将四边形ACDB的面积分成2:3两部分,
∴S△BDE=S矩形ABDC=×20=8,
∵S△BDE=BD BE=×5BE=8,
∴BE=
过P点作PH⊥BD交DB的延长线于点H,
∵B(6,4),
∴PH=6
S△PDB=BD×PH=×5×6=15,
∴S△PBE=S△PDB﹣S△BDE=15﹣8=7,
∵S△PBE=BE PG=PG=7,
∴PG=,
∴PO=PG+OG=+4=,
∴P(0,),
即:点P坐标为(0,5)或(0,).
答案第1页,共2页
答案第1页,共2页
一、单选题
1.下列道路交通标志图中,是中心对称图形的是( )
A. B. C.D.
2.下列图形中,是中心对称图形,但不是轴对称图形的是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
3.在平面直角坐标系中,已知,现将A点绕原点O顺时针旋转90°得到,则的坐标是( )
A. B. C. D.
4.如图,在△ABC中,AB=4,AC=3,∠BAC=30°,将△ABC绕点A按逆时针旋转60°得到△A1B1C1连接BC1,则BC1的长为( )
A.3 B.4 C.5 D.6
5.如图,将绕点顺时针旋转60°得到,若,则等于( )
A.2cm B.3cm C.4cm D.5cm
6.如图,在△ABC中,AC=BC,∠C=40°.将△ABC绕着点B逆时针方向旋转得△DBE,其中AC∥BD,BF、BG分别为△ABC与△DBE的中线,则∠FBG=( )
A.90° B.80° C.75° D.70°
7.如图,在平面直角坐标系中,△ABC的顶点都在方格线的格点上,将三角形ABC绕点P旋转90°,得到△A′B′C′,则点P的坐标为( )
A.(0,4) B.(1,1) C.(1,2) D.(2,1)
8.如图,P是平分线上一点,OP=10,,在绕点P旋转的过程中始终保持不变,其两边和OA,OB分别相交于M,N,下列结论:①是等边三角形;②MN的值不变;③OM+ON=10;④四边形PMON面积不变.其中正确结论的个数为( )
A.4 B.3 C.2 D.1
二、填空题
9.在平面直角坐标系中,把点向左平移一个单位得到点A′,则点A′关于原点对称的点A″的坐标为________.
10.如图所示,在△ABC中,∠ACB=90°,∠A=20°,将△ABC绕点C旋转到△DEC的位置,D点刚好落在AB边上,则∠ACE的度数为______度.
11.如图,在长方形ABCD中,AB=2cm,BC=3cm,E、F分别是AD、BC的中点,如果将长方形ABFE绕点F顺时针旋转90°,那么旋转后的长方形与长方形CDEF重叠部分的面积是_____cm2.
12.如图,在中,,,,将绕点按逆时针方向旋转得到,连接,,直线,相交于点,连接,在旋转过程中,线段的最大值为__________.
13.边长相等、各内角均为120°的六边形ABCDEF在直角坐标系内的位置如图所示,,点B在原点,把六边形ABCDEF沿x轴正半轴绕顶点按顺时针方向,从点B开始逐次连续旋转,每次旋转60°,经过2021次旋转之后,点B的坐标是_____________.
三、解答题
14.如图,将△ABC绕点B顺时针旋转得到△DBE,使得点D落在线段AC上.若AC=BC,求证:BE∥AC.
15.如图,在平面直角坐标系xOy中,是由ABC平移得到,已知,,三点的坐标分别为,,,点A的坐标为.
(1)画出ABC.
(2)描述ABC到的平移过程.
(3)已知点P(0,b)为ABC内的一点,求点P在内的对应点的坐标.
16.如图,在Rt△ABC中,∠BAC=90°,∠ACB=30°,将△ABC绕点C逆时针旋转60°得到△CDE,点A、B的对应点分别是D、E,点F是边BC中点,连结AD、EF.
(1)求证:△ACD是等边三角形;
(2)判断AD与EF有怎样的数量关系,并说明理由.
17.在平面直角坐标系中,已知点,,连接AB,将AB向下平移5个单位得线段CD,其中点A的对应点为点C.
(1)填空:点C的坐标为______,线段AB平移到CD扫过的面积为______;
(2)若点P是y轴上的动点,连接PD.
①如图(1),当点P在y轴正半轴时,线段PD与线段AC相交于点E,用等式表示三角形PEC的面积与三角形ECD的面积之间的关系,并说明理由;
②当PD将四边形ACDB的面积分成2:3两部分时,求点P的坐标.
试卷第1页,共3页
参考答案:
1.C
【解析】
解:A、不是中心对称图形,本选项不符合题意;
B、不是中心对称图形,本选项不符合题意;
C、是中心对称图形,本选项符合题意;
D、不是中心对称图形,本选项不符合题意.
故选:C.
2.D
【解析】
解:A中正方形既是中心对称图形又是轴对称图形,不符合题意;
B中矩形既是中心对称图形又是轴对称图形,不符合题意;
C中菱形既是中心对称图形又是轴对称图形,不符合题意;
D平行四边形是中心对称图形但不是轴对称图形,符合题意;
故选D.
3.B
【解析】
解:,现将A点绕原点O顺时针旋转90°得到,则的坐标是
故选B
4.C
【解析】
解:由旋转的定义和性质可得AC1=AC=3,∠B1AC1=∠BAC=30°,∠BAB1=60°.
∴∠BAC1=90°.
∴在Rt△BAC1中,利用勾股定理可得BC1==5.
故选:C.
5.B
【解析】
解:∵△ABC绕点A顺时针旋转60°得到△AED,
∴AB=AE,∠BAE=60°,
∴△AEB是等边三角形,
∴BE=AB,
∵AB=3cm,
∴BE=3cm.
故选:B.
6.D
【解析】
解:,
,
,
,
由旋转可知,点绕点旋转后的对应点分别为点,
,
故选:D.
7.C
【解析】
解:选两组对应点,连接后作其中垂线,两中垂线的交点即为点P,由图知,旋转中心P的坐标为(1,2)
故选:C.
8.B
【解析】
如图作PE⊥OA于E,PF⊥OB于F.
∵∠PEO=∠PFO=90°,
∴∠EPF+∠AOB=180°,
∵∠MPN+∠AOB=180°,
∴∠EPF=∠MPN,
∴∠EPM=∠FPN,
∵OP平分∠AOB,PE⊥OA于E,PF⊥OB于F,
∴PE=PF,
在Rt△POE和Rt△POF中,
,
∴Rt△POE≌Rt△POF(HL),
∴OE=OF,
在△PEM和△PFN中,
,
∴△PEM≌△PFN(ASA),
∴EM=NF,PM=PN,S△PEM=S△PNF,
∵
∴是等边三角形,故①正确;
∵S△PEM=S△PNF,
∴S四边形PMON=S四边形PEOF=定值,故④正确;
∵OM+ON=OE+ME+OF-NF=2OE=10,故③正确;
∵M,N的位置变化,
∴MN的长度是变化的,故②错误;
故选:B.
9.(-1,-3)
【解析】
根据平移方式可知点的坐标为(1,3),
∴点关于原点对称的点的坐标为(-1,-3).
故答案为:(-1,-3).
10.40
【解析】
解:∵∠ACB=90°,∠A=20°,
∴∠B=70°;
由题意得:BC=DC,
∴∠CDB=∠B=70°,
∴∠BCD=180°-40°,
∴∠ACE=∠BCD=40°.
故答案为:40
11.2.25
【解析】
解:如图,将长方形ABFE绕点F顺时针旋转90度,得到长方形A′B′FE′,设A′B′与DC交于点G,
则FC=FB=FB′=BC=1.5cm,
所以旋转后的长方形A′B′FE′与长方形CDEF重叠部分B′FCG是正方形,边长为1.5cm,
所以,面积S=1.5×1.5=2.25(cm2).
故答案是:2.25.
12.
【解析】
解:取AB的中点H,连接CH、FH,设EC,DF交于点G,
在△ABC中,∠ACB=90 ,
∵AC=,BC=2,
∴AB=,
由旋转可知:△DCE≌△ACB,
∴∠DCE=∠ACB,DC=AC,CE=CB,
∴∠DCA=∠BCE,
∵∠ADC=(180 -∠ACD) ,∠BEC= (180 -∠BCE),
∴∠ADC=∠BEC,
∵∠DGC=∠EGF,
∴∠DCG=∠EFG=90 ,
∴∠AFB=90 ,
∵H是AB的中点,
∴FH=AB,
∵∠ACB=90 ,
∴CH=AB,
∴FH=CH=AB=,
在△FCH中,FH+CH>CF,
当F、C、H在一条直线上时,CF有最大值,
∴线段CF的最大值为.
故答案为:
13.
【解析】
∵正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,
∴每6次翻转为一个循环组循环,
∵,
∴经过2021次翻转为第337循环组的第5次翻转,点B在开始时点C的位置,
∵,
∴,
∴翻转前进的距离为:,
如图,过点B作BG⊥x于G,
则∠BAG=60°,
∴,
,
∴,
∴点B的坐标为.
故答案为:.
14.证明见解析.
【解析】
证明:,
,
由旋转的性质得:,,
,
,
.
15.(1)见解析
(2)向下平移3个单位长度
(3)
【解析】
(1)
解:根据题意可得:,,得出点A到向下移动三个单位长度,
∴,,
依次连接各点,作图如下:
(2)
解:根据图形及坐标可得:向下平移3个单位长度得;
(3)
解:∵由(2)可得:向下平移3个单位长度得,点P的坐标为,
∴根据平移的性质得对应点P的坐标为.
16.(1)见解析过程;
(2)AD=EF,理由见解析过程.
【解析】
(1)
证明:∵将△ABC绕点C逆时针旋转60°得到△CDE,
∴AC=CD,∠ACD=60°,
∴△ACD是等边三角形;
(2)
解:AD=EF,理由如下:
∵将△ABC绕点C逆时针旋转60°得到△CDE,
∴∠BCE=60°,BC=CE,
∵△ACD是等边三角形,
∴AD=AC,
∵点F是边BC中点,
∴BC=2CF,
∵∠BAC=90°,∠ACB=30°,
∴BC=2AB,∠ABC=60°=∠BCE,
∴AB=CF,
在△ABC和△DEC中,
,
∴△ABC≌△FCE(SAS),
∴EF=AC,
∴AD=EF.
17.(1)
(2)①S△PEC=S△ECD,理由见解析;②点P坐标为(0,5)或(0,).
【解析】
(1)
解:将AB向下平移5个单位得线段CD,
线段AB平移到CD扫过的面积为:
故答案为:
(2)
①如图1,过P点作PF⊥AC于F,
由平移知,轴,
∵A(2,4),
∴PF=2,
由平移知,CD=AB=4,
∴S△PEC=CE PF=CE×2=CE,S△ECD=CE CD=CE×4=2CE,
∴S△ECD=2S△PEC,
即:S△PEC=S△ECD;
②(ⅰ)如图2,当PD交线段AC于E,且PD将四边形ACDB分成面积为2:3两部分时,
连接PC,延长DC交y轴于点M,则M(0,﹣1),
∴OM=1,
连接AC,则S△ACD=S长方形ABDC=10,
∵PD将四边形ACDB的面积分成2:3两部分,
∴S△CDE=S矩形ABDC=×20=8,
由①知,S△PEC=S△ECD=×8=4,
∴S△PCD=S△PEC+S△ECD=4+8=12,
∵S△PCD=CD PM=×4PM=12,
∴PM=6,
∴PO=PM﹣OM=6﹣1=5,
∴P(0,5).
(ⅱ)如图3,当PD交AB于点F,PD将四边形ACDB分成面积为2:3两部分时,
连接PB,延长BA交y轴于点G,则G(0,4),
∴OG=4,连接AC,则S△ABD=S长方形ABDC=10,
∵PD将四边形ACDB的面积分成2:3两部分,
∴S△BDE=S矩形ABDC=×20=8,
∵S△BDE=BD BE=×5BE=8,
∴BE=
过P点作PH⊥BD交DB的延长线于点H,
∵B(6,4),
∴PH=6
S△PDB=BD×PH=×5×6=15,
∴S△PBE=S△PDB﹣S△BDE=15﹣8=7,
∵S△PBE=BE PG=PG=7,
∴PG=,
∴PO=PG+OG=+4=,
∴P(0,),
即:点P坐标为(0,5)或(0,).
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
