2021-2022学年湘教版数学八年级下册2.2.2平行四边形的判定课后提升练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版数学八年级下册2.2.2平行四边形的判定课后提升练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 848.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 00:00:00 | ||
图片预览



文档简介
平行四边形的判定
一、单选题
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD B.AB=CD,AO=CO
C.AB=CD,AD=BC D.∠BAD=∠BCD,AB∥CD
2.如图,在四边形中,,要使四边形成为平行四边形,则应增加的条件是( )
A. B.
C. D.
3.如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O.下列条件:①AD∥BC,②AB=CD,③AD=BC,④∠ADC=∠ABC,⑤BO=DO,⑥∠DBA=∠CAB.若添加其中一个,可得到该四边形是平行四边形,则添加的条件可以是( )
A.①②③⑤ B.①②④⑤ C.①②④⑥ D.①③④⑥
4.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是( )
A.①② B.①④ C.②③ D.②④
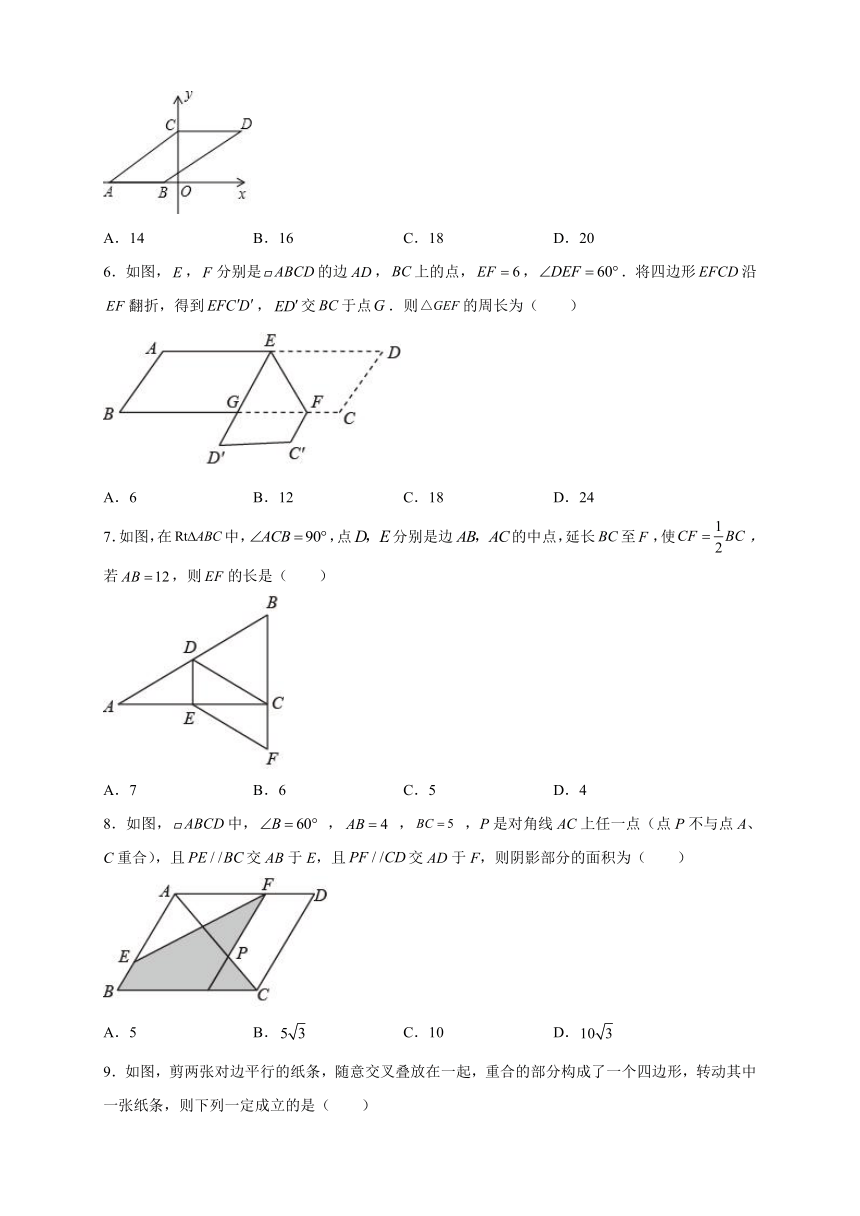
5.已知:如图,点A(,0),B(,0),将线段AB平移后得到线段CD,点A的对应点C恰好落在y轴上,且四边形ABDC的面积为9,则四边形ABDC的周长是( )
A.14 B.16 C.18 D.20
6.如图,,分别是的边,上的点,,.将四边形沿翻折,得到,交于点.则的周长为( )
A.6 B.12 C.18 D.24
7.如图,在中,,点分别是边的中点,延长至,使,若,则的长是( )
A.7 B.6 C.5 D.4
8.如图,中, , , ,P是对角线AC上任一点(点P不与点A、C重合),且交AB于E,且交AD于F,则阴影部分的面积为( )
A.5 B. C.10 D.
9.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,则下列一定成立的是( )
A. B. C. D.
10.如图,点A,B,C在同一直线上,点D,E,F,G在同一直线上,且.图中平行四边形有( )个
A.4 B.5 C.3 D.6
11.如图,在平面直角坐标系中,点,,的坐标分别是,,,再找一点,使它与点,,构成的四边形是平行四边形,则点的坐标不可能是( )
A. B. C. D.
12.如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧相交于点D,分别连接AB,AD,CD,则四边形ABCD的( )
A.四条边相等 B.四个角相等 C.对角线互相垂直 D.对角线互相平分
13.如图1,中,,为锐角.要在对角线上找点,,使四边形为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( )
图2
A.甲、乙、丙都是 B.只有甲、乙才是
C.只有甲、丙才是 D.只有乙、丙才是
14.如图,将绕边的中点O顺时针旋转.嘉淇发现,旋转后的与构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵,”和“∴四边形…”之间作补充,下列补充不正确的是( )
点A,C分别转到了点C,A处, 而点B转到了点D处. ∵, ∴四边形是平行四边形.
A.应补充:且 B.应补充:且
C.应补充:且 D.应补充:且
15.如图,在等边△ABC中,BC=8cm,射线AGBC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以3cm/s的速度运动.设运动时间为t(s),当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形.
A.1或2 B.2 C.2或3 D.2或4
二、填空题
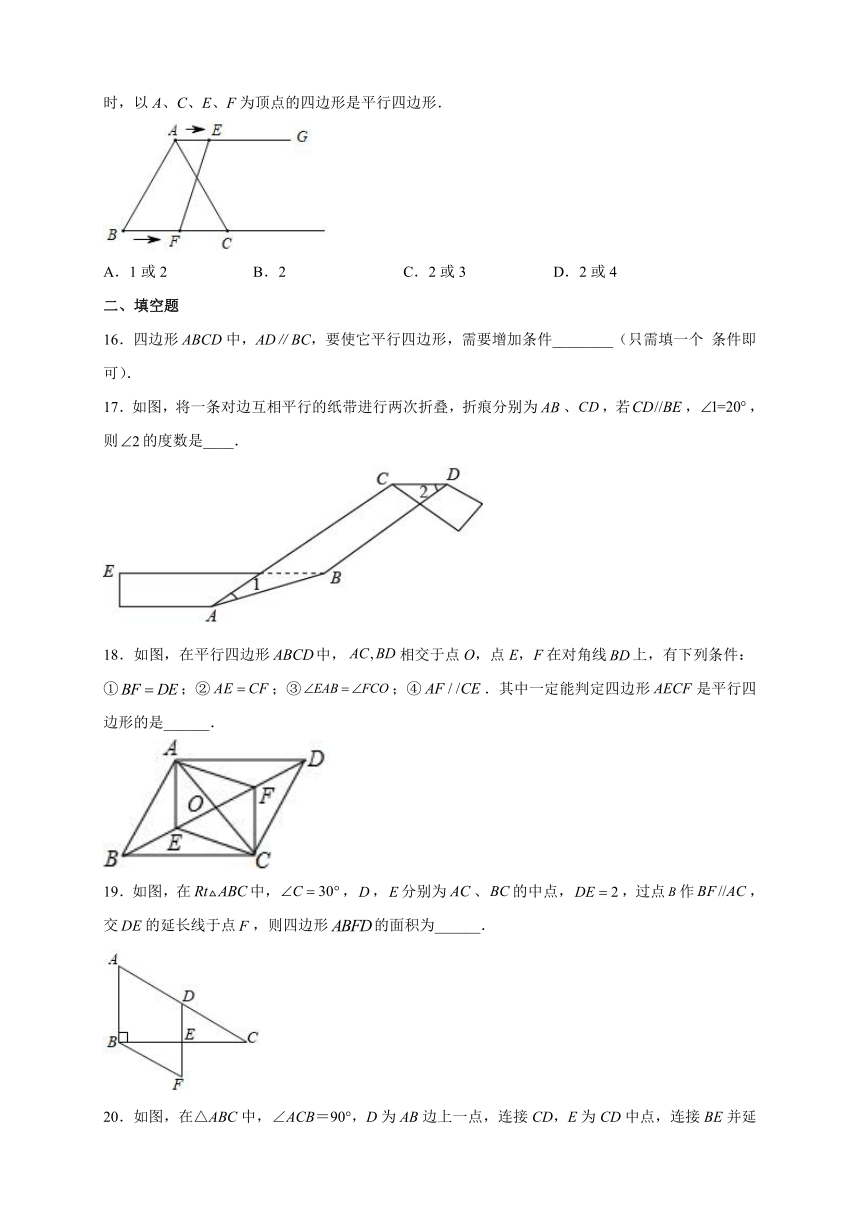
16.四边形ABCD中,AD∥BC,要使它平行四边形,需要增加条件________(只需填一个 条件即可).
17.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、,若,,则的度数是____.
18.如图,在平行四边形中,相交于点O,点E,F在对角线上,有下列条件:①;②;③;④.其中一定能判定四边形是平行四边形的是______.
19.如图,在中,,,分别为、的中点,,过点作,交的延长线于点,则四边形的面积为______.
20.如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.若∠A=30°,BC=2,CF=3,则CD=__.
三、解答题
21.如图,和均为等腰三角形,且,点是的中点,求证;四边形是平行四边形 .
22.如图,平行四边形中,是它的一条对角线,过、两点作,,垂足分别为、,延长、分别交、于、.
(1)求证:四边形是平行四边形;
(2)求证:.
23.如图,的对角线与相交于点O,E,F是上的两点.
(1)当满足什么条件时,四边形是平行四边形?请说明理由;
(2)当与满足什么条件时,四边形是平行四边形?请说明理由.
24.如图,在△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°能与△DEC重合,点F是边AC中点.
(1)求证:△CFD≌△ABC;
(2)连接BE,求证:四边形BEDF是平行四边形.
25.如图,在中,,,将绕点C顺时针旋转一定的角度得到,点A,B的对应点分别是点D,E.
(1)如图①,当点E恰好在AC边上时,连接AD,求∠ADE的度数;
(2)如图②,当时,若点F为AC边上的动点,当∠FBC为何值时,四边形BFDE为平行四边形?请说出你的结论并加以证明
试卷第1页,共3页
参考答案:
1.B
解:略
2.B
解:A.错误,当四边形是等腰梯形时,也满足条件.
B.正确,∵,
∴,
∵,
∴四边形是平行四边形.
C.错误,当四边形是等腰梯形时,也满足条件.
D.错误,∵,
∴,与题目条件重复,无法判断四边形是不是平行四边形.
故选:B.
3.B
解:①∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,故①正确;
②∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,故②正确;
③∵AB∥CD,AD=BC无法得出四边形ABCD是平行四边形,故③不正确;
④∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ADC=∠ABC,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形,故④正确;
⑤∵AB∥CD,
∴∠ABO=∠CDO,
在△AOB和△COD中,
,
∴△AOB≌△COD(ASA),
∴AO=CO,
又∵OB=OD,
∴四边形ABCD为平行四边形,故⑤正确;
∵∠BCD+∠ADC=180°,
∴AD∥BC,
又∵AB∥CD,
∴四边形ABCD是平行四边形,故选项C不符合题意;
⑥∵∠DBA=∠CAB,
∴OA=OB,
∵AB∥CD,
∴∠DBA=∠CDB,∠CAB=∠ACD,
∵∠DBA=∠CAB,
∴∠CDB=∠ACD,
∴OC=OD,
不能得出四边形ABCD是平行四边形,故⑥不正确;
故选:B.
4.C
解:∵只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故选:C.
5.B
解:由题意可知:,
∴四边形ABDC为平行四边形
四边形ABDC的面积为9,即
解得
由勾股定理可得:
四边形ABDC的周长
故选B.
6.C
解:由折叠得:∠DEF=∠D′EF=60°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DEF=∠EFG=60°,
∴△GEF是等边三角形,
∴EF=FG=GE=6,
∴△GEF的周长为6×3=18,
故选:C.
7.B
解:分别是边的中点,
,
,
,
四边形是平行四边形,
,
,
故选:B.
8.B
解:∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC
∵PE∥BC,
∴PE∥AD
∵PF∥CD,
∴PF∥AB,
∴四边形AEPF为平行四边形.
设平行四边形AEPF的对角线AP、EF相交于O,则AO=PO,EO=FO,∠AOE=∠POF
∴△POF≌△AOE,
∴图中阴影部分的面积等于△ABC的面积,
过A作AM⊥BC交BC于M,
∵∠B=60°,AB=4,
∴BM=2
∴AM= =2,
S△ABC5×25,即阴影部分的面积等于5.
故答案选:B.
9.B
解:由题意得:,
四边形是平行四边形,
,即选项一定成立,
四边形不一定是菱形,也不一定是矩形,
∴选项不一定成立,
故选:B.
10.B
解:如图,
图中的平行四边形有: ABED, ABGF, BCFE, ACFD, PBQF,
故选B.
11.D
解:如图所示,若以AC、BC为邻边平构成平行四边形,可得此时D1点的坐标为(2,4);若以AB、AC为邻边构成平行四边形,可得此时D2点的坐标为(-4,2),以AB、BC为邻边构成平行四边形,可得此时D3点的坐标(0,-4),故点D的坐标不可能是.
故选:D.
12.D
解:∵分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,
∴AD=BC,AB=CD,
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形),
∴平行四边形ABCD的对角线互相平分,
故选:D.
13.A
解:连接交于点
甲方案:四边形是平行四边形
四边形为平行四边形.
乙方案:
四边形是平行四边形
,,
又
(AAS)
四边形为平行四边形.
丙方案:
四边形是平行四边形
,,,
又分别平分
, 即
(ASA)
四边形为平行四边形.
所以甲、乙、丙三种方案都可以.
故选A.
14.C
解:A.加上,可证得时间△ABC和△CDA全等,可得AB=CD,可得四边形是平行四边形;
B.加上,根据“两组对边分别相等的四边形是平行四边形”,可得四边形是平行四边形;
C.加上,一组对边平行,另一组对边相等的四边形可能是等腰梯形;
D.加上,根据“一组对边平行且相等的四边形是平行四边形”,可得四边形是平行四边形.
故选:C
15.D
解:当点F在C的左侧时,根据题意得:AE=tcm,BF=3tcm,
则CF=BC﹣BF=(8﹣3t)cm,
∵AG∥BC,
∴当AE=CF时,四边形AECF是平行四边形,
即t=8﹣3t,
解得:t=2;
当点F在C的右侧时,根据题意得:AE=tcm,BF=3tcm,
则CF=BF﹣BC=(3t﹣8)cm,
∵AG∥BC,
∴当AE=CF时,四边形AEFC是平行四边形,
即t=3t﹣8,
解得:t=4;
综上可得:当t=2或4s时,以A、C、E、F为顶点四边形是平行四边形,
故选:D.
16.AD=BC
解:略
17.40°
解:如图所示:
∵,
由折叠的性质可得,
∵,
∴,
∴,
∵,
∴四边形是平行四边形,
∴;
故答案为40°.
18.①④
解:①∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,OB=OD,OA=OC,
∵BF=DE,
∴BF-OB=DE-OD,
即OF=OE,
∴四边形AECF是平行四边形;
②∵AE=CF,不能判定△ABE≌△CDF,
∴不能判定四边形AECF是平行四边形;
③∠EAB=∠FCO不能判定四边形AECF是平行四边形;
④∵AF∥CE,
∴∠AFB=∠CED,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(AAS),
∴BF=DE,
∴BF-OB=DE-OD,
即OF=OE,
又∵OA=OC,
∴四边形AECF是平行四边形;
故答案为:①④.
19.
解:∵,分别为、的中点,,
∴AB=2DE=4,,
∵在中,,
∴AC=2AB=8,
∴BC===,
又∵点E为BC中点,
∴BE=BC=,
∵,,
∴四边形ABFD为平行四边形,
∴四边形的面积=AB×BE=4×=,
故答案为:.
20.
解:∵点E为CD中点,
∴CE=DE.
∵EF=BE,
∴四边形DBCF是平行四边形.
∴CF∥AB,DF∥BC.
∴∠FCG=∠A=30°,∠CGF=∠CGD=∠ACB=90°.
在Rt△FCG中,CF=3,
∴FG=,CG=.
∵DF=BC=2,
∴DG=.
在Rt△DCG中,CD==.
故答案为:.
21.证明见解析.
证明:为等腰三角形,,是的中点,
,,
是等腰三角形,,
,,
,,
四边形是平行四边形.
22.(1)见解析;(2)见解析
证明:(1)∵四边形是平行四边形,
∴,
即,
∵,,
∴,
∴四边形是平行四边形;
(2)∵四边形是平行四边形,
∴,,
∴,
∵四边形是平行四边形,
∴,
∴,
∵,,
∴,
∴.
23.(1),理由见解析;(2),理由见解析
解:(1),理由如下,
四边形是平行四边形
,
四边形是平行四边形;
(2),理由如下,
四边形是平行四边形
又
四边形是平行四边形.
24.(1)见解析 (2)见解析
(1)
证明:点是边中点,
,
,
,,
,
将绕点顺时针旋转得到,
,,
,
在和中,
,
;
(2)
延长交于点,
由(1)得,,
,
,
,
,
,
,,
,
四边形是平行四边形.
25.(1)15° (2)∠FBC=30°,理由见详解
(1)
解:∵将绕点C顺时针旋转一定的角度α得到△DEC,E点在AC上,
∴CA=CD,∠ECD=∠BCA=30,
∴∠CAD=∠CDA=(180 30)=75,
又∵∠DEC=∠ABC=90,
∴∠ADE=90°-75=15;
(2)
∠FBC=30时,四边形BFDE为平行四边形,
∴∠FBC=∠ACB=30,
∴∠ABF=∠A=60,
∴BF=CF=AF,
∴是等边三角形,
∴BF=AB,
∵将ABC绕点C顺时针旋转60得到,
∴DE=AB,是等边三角形,∠DEC=∠ABC=90,
∴∠CBE=∠BEC=60,
∴∠EBF=∠EBC-∠FBC=30,
∴∠DEB+∠EBF=180,
∴DE=BF,,
∴四边形BFDE为平行四边形.
答案第1页,共2页
一、单选题
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD B.AB=CD,AO=CO
C.AB=CD,AD=BC D.∠BAD=∠BCD,AB∥CD
2.如图,在四边形中,,要使四边形成为平行四边形,则应增加的条件是( )
A. B.
C. D.
3.如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O.下列条件:①AD∥BC,②AB=CD,③AD=BC,④∠ADC=∠ABC,⑤BO=DO,⑥∠DBA=∠CAB.若添加其中一个,可得到该四边形是平行四边形,则添加的条件可以是( )
A.①②③⑤ B.①②④⑤ C.①②④⑥ D.①③④⑥
4.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是( )
A.①② B.①④ C.②③ D.②④
5.已知:如图,点A(,0),B(,0),将线段AB平移后得到线段CD,点A的对应点C恰好落在y轴上,且四边形ABDC的面积为9,则四边形ABDC的周长是( )
A.14 B.16 C.18 D.20
6.如图,,分别是的边,上的点,,.将四边形沿翻折,得到,交于点.则的周长为( )
A.6 B.12 C.18 D.24
7.如图,在中,,点分别是边的中点,延长至,使,若,则的长是( )
A.7 B.6 C.5 D.4
8.如图,中, , , ,P是对角线AC上任一点(点P不与点A、C重合),且交AB于E,且交AD于F,则阴影部分的面积为( )
A.5 B. C.10 D.
9.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,则下列一定成立的是( )
A. B. C. D.
10.如图,点A,B,C在同一直线上,点D,E,F,G在同一直线上,且.图中平行四边形有( )个
A.4 B.5 C.3 D.6
11.如图,在平面直角坐标系中,点,,的坐标分别是,,,再找一点,使它与点,,构成的四边形是平行四边形,则点的坐标不可能是( )
A. B. C. D.
12.如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧相交于点D,分别连接AB,AD,CD,则四边形ABCD的( )
A.四条边相等 B.四个角相等 C.对角线互相垂直 D.对角线互相平分
13.如图1,中,,为锐角.要在对角线上找点,,使四边形为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( )
图2
A.甲、乙、丙都是 B.只有甲、乙才是
C.只有甲、丙才是 D.只有乙、丙才是
14.如图,将绕边的中点O顺时针旋转.嘉淇发现,旋转后的与构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵,”和“∴四边形…”之间作补充,下列补充不正确的是( )
点A,C分别转到了点C,A处, 而点B转到了点D处. ∵, ∴四边形是平行四边形.
A.应补充:且 B.应补充:且
C.应补充:且 D.应补充:且
15.如图,在等边△ABC中,BC=8cm,射线AGBC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以3cm/s的速度运动.设运动时间为t(s),当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形.
A.1或2 B.2 C.2或3 D.2或4
二、填空题
16.四边形ABCD中,AD∥BC,要使它平行四边形,需要增加条件________(只需填一个 条件即可).
17.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、,若,,则的度数是____.
18.如图,在平行四边形中,相交于点O,点E,F在对角线上,有下列条件:①;②;③;④.其中一定能判定四边形是平行四边形的是______.
19.如图,在中,,,分别为、的中点,,过点作,交的延长线于点,则四边形的面积为______.
20.如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.若∠A=30°,BC=2,CF=3,则CD=__.
三、解答题
21.如图,和均为等腰三角形,且,点是的中点,求证;四边形是平行四边形 .
22.如图,平行四边形中,是它的一条对角线,过、两点作,,垂足分别为、,延长、分别交、于、.
(1)求证:四边形是平行四边形;
(2)求证:.
23.如图,的对角线与相交于点O,E,F是上的两点.
(1)当满足什么条件时,四边形是平行四边形?请说明理由;
(2)当与满足什么条件时,四边形是平行四边形?请说明理由.
24.如图,在△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°能与△DEC重合,点F是边AC中点.
(1)求证:△CFD≌△ABC;
(2)连接BE,求证:四边形BEDF是平行四边形.
25.如图,在中,,,将绕点C顺时针旋转一定的角度得到,点A,B的对应点分别是点D,E.
(1)如图①,当点E恰好在AC边上时,连接AD,求∠ADE的度数;
(2)如图②,当时,若点F为AC边上的动点,当∠FBC为何值时,四边形BFDE为平行四边形?请说出你的结论并加以证明
试卷第1页,共3页
参考答案:
1.B
解:略
2.B
解:A.错误,当四边形是等腰梯形时,也满足条件.
B.正确,∵,
∴,
∵,
∴四边形是平行四边形.
C.错误,当四边形是等腰梯形时,也满足条件.
D.错误,∵,
∴,与题目条件重复,无法判断四边形是不是平行四边形.
故选:B.
3.B
解:①∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,故①正确;
②∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,故②正确;
③∵AB∥CD,AD=BC无法得出四边形ABCD是平行四边形,故③不正确;
④∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ADC=∠ABC,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形,故④正确;
⑤∵AB∥CD,
∴∠ABO=∠CDO,
在△AOB和△COD中,
,
∴△AOB≌△COD(ASA),
∴AO=CO,
又∵OB=OD,
∴四边形ABCD为平行四边形,故⑤正确;
∵∠BCD+∠ADC=180°,
∴AD∥BC,
又∵AB∥CD,
∴四边形ABCD是平行四边形,故选项C不符合题意;
⑥∵∠DBA=∠CAB,
∴OA=OB,
∵AB∥CD,
∴∠DBA=∠CDB,∠CAB=∠ACD,
∵∠DBA=∠CAB,
∴∠CDB=∠ACD,
∴OC=OD,
不能得出四边形ABCD是平行四边形,故⑥不正确;
故选:B.
4.C
解:∵只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故选:C.
5.B
解:由题意可知:,
∴四边形ABDC为平行四边形
四边形ABDC的面积为9,即
解得
由勾股定理可得:
四边形ABDC的周长
故选B.
6.C
解:由折叠得:∠DEF=∠D′EF=60°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DEF=∠EFG=60°,
∴△GEF是等边三角形,
∴EF=FG=GE=6,
∴△GEF的周长为6×3=18,
故选:C.
7.B
解:分别是边的中点,
,
,
,
四边形是平行四边形,
,
,
故选:B.
8.B
解:∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC
∵PE∥BC,
∴PE∥AD
∵PF∥CD,
∴PF∥AB,
∴四边形AEPF为平行四边形.
设平行四边形AEPF的对角线AP、EF相交于O,则AO=PO,EO=FO,∠AOE=∠POF
∴△POF≌△AOE,
∴图中阴影部分的面积等于△ABC的面积,
过A作AM⊥BC交BC于M,
∵∠B=60°,AB=4,
∴BM=2
∴AM= =2,
S△ABC5×25,即阴影部分的面积等于5.
故答案选:B.
9.B
解:由题意得:,
四边形是平行四边形,
,即选项一定成立,
四边形不一定是菱形,也不一定是矩形,
∴选项不一定成立,
故选:B.
10.B
解:如图,
图中的平行四边形有: ABED, ABGF, BCFE, ACFD, PBQF,
故选B.
11.D
解:如图所示,若以AC、BC为邻边平构成平行四边形,可得此时D1点的坐标为(2,4);若以AB、AC为邻边构成平行四边形,可得此时D2点的坐标为(-4,2),以AB、BC为邻边构成平行四边形,可得此时D3点的坐标(0,-4),故点D的坐标不可能是.
故选:D.
12.D
解:∵分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,
∴AD=BC,AB=CD,
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形),
∴平行四边形ABCD的对角线互相平分,
故选:D.
13.A
解:连接交于点
甲方案:四边形是平行四边形
四边形为平行四边形.
乙方案:
四边形是平行四边形
,,
又
(AAS)
四边形为平行四边形.
丙方案:
四边形是平行四边形
,,,
又分别平分
, 即
(ASA)
四边形为平行四边形.
所以甲、乙、丙三种方案都可以.
故选A.
14.C
解:A.加上,可证得时间△ABC和△CDA全等,可得AB=CD,可得四边形是平行四边形;
B.加上,根据“两组对边分别相等的四边形是平行四边形”,可得四边形是平行四边形;
C.加上,一组对边平行,另一组对边相等的四边形可能是等腰梯形;
D.加上,根据“一组对边平行且相等的四边形是平行四边形”,可得四边形是平行四边形.
故选:C
15.D
解:当点F在C的左侧时,根据题意得:AE=tcm,BF=3tcm,
则CF=BC﹣BF=(8﹣3t)cm,
∵AG∥BC,
∴当AE=CF时,四边形AECF是平行四边形,
即t=8﹣3t,
解得:t=2;
当点F在C的右侧时,根据题意得:AE=tcm,BF=3tcm,
则CF=BF﹣BC=(3t﹣8)cm,
∵AG∥BC,
∴当AE=CF时,四边形AEFC是平行四边形,
即t=3t﹣8,
解得:t=4;
综上可得:当t=2或4s时,以A、C、E、F为顶点四边形是平行四边形,
故选:D.
16.AD=BC
解:略
17.40°
解:如图所示:
∵,
由折叠的性质可得,
∵,
∴,
∴,
∵,
∴四边形是平行四边形,
∴;
故答案为40°.
18.①④
解:①∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,OB=OD,OA=OC,
∵BF=DE,
∴BF-OB=DE-OD,
即OF=OE,
∴四边形AECF是平行四边形;
②∵AE=CF,不能判定△ABE≌△CDF,
∴不能判定四边形AECF是平行四边形;
③∠EAB=∠FCO不能判定四边形AECF是平行四边形;
④∵AF∥CE,
∴∠AFB=∠CED,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(AAS),
∴BF=DE,
∴BF-OB=DE-OD,
即OF=OE,
又∵OA=OC,
∴四边形AECF是平行四边形;
故答案为:①④.
19.
解:∵,分别为、的中点,,
∴AB=2DE=4,,
∵在中,,
∴AC=2AB=8,
∴BC===,
又∵点E为BC中点,
∴BE=BC=,
∵,,
∴四边形ABFD为平行四边形,
∴四边形的面积=AB×BE=4×=,
故答案为:.
20.
解:∵点E为CD中点,
∴CE=DE.
∵EF=BE,
∴四边形DBCF是平行四边形.
∴CF∥AB,DF∥BC.
∴∠FCG=∠A=30°,∠CGF=∠CGD=∠ACB=90°.
在Rt△FCG中,CF=3,
∴FG=,CG=.
∵DF=BC=2,
∴DG=.
在Rt△DCG中,CD==.
故答案为:.
21.证明见解析.
证明:为等腰三角形,,是的中点,
,,
是等腰三角形,,
,,
,,
四边形是平行四边形.
22.(1)见解析;(2)见解析
证明:(1)∵四边形是平行四边形,
∴,
即,
∵,,
∴,
∴四边形是平行四边形;
(2)∵四边形是平行四边形,
∴,,
∴,
∵四边形是平行四边形,
∴,
∴,
∵,,
∴,
∴.
23.(1),理由见解析;(2),理由见解析
解:(1),理由如下,
四边形是平行四边形
,
四边形是平行四边形;
(2),理由如下,
四边形是平行四边形
又
四边形是平行四边形.
24.(1)见解析 (2)见解析
(1)
证明:点是边中点,
,
,
,,
,
将绕点顺时针旋转得到,
,,
,
在和中,
,
;
(2)
延长交于点,
由(1)得,,
,
,
,
,
,
,,
,
四边形是平行四边形.
25.(1)15° (2)∠FBC=30°,理由见详解
(1)
解:∵将绕点C顺时针旋转一定的角度α得到△DEC,E点在AC上,
∴CA=CD,∠ECD=∠BCA=30,
∴∠CAD=∠CDA=(180 30)=75,
又∵∠DEC=∠ABC=90,
∴∠ADE=90°-75=15;
(2)
∠FBC=30时,四边形BFDE为平行四边形,
∴∠FBC=∠ACB=30,
∴∠ABF=∠A=60,
∴BF=CF=AF,
∴是等边三角形,
∴BF=AB,
∵将ABC绕点C顺时针旋转60得到,
∴DE=AB,是等边三角形,∠DEC=∠ABC=90,
∴∠CBE=∠BEC=60,
∴∠EBF=∠EBC-∠FBC=30,
∴∠DEB+∠EBF=180,
∴DE=BF,,
∴四边形BFDE为平行四边形.
答案第1页,共2页
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
