2021--2022学年苏科版九年级数学下册7.1正切(1)培优训练(Word版含答案)
文档属性
| 名称 | 2021--2022学年苏科版九年级数学下册7.1正切(1)培优训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 428.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 21:33:23 | ||
图片预览




文档简介
7.1正切(1)-苏科版九年级数学下册 培优训练
一、选择题
1、在Rt△ABC中,若∠C=90°,AC=4,AB=5,则tanB=( )
A、 B、 C、 D、
2.在中,,若,则( )
A. B. C. D.
3、如图,已知Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长是( )
A.2 B.8 C.2 D.
4、如图,一个斜坡长130 m,坡顶离水平地面的距离为50 m,
那么这个斜坡与水平地面夹角的正切值等于( )
A. B. C. D.
5、在Rt△ABC中,∠C=90°,AB=5,BC=3,则tanA的值是( )
A. B. C. D.
6、如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=16,tan∠ABD=,则线段AB的长为( )
A. B.10 C.5 D.2
7、如图,四边形ABCD内接于⊙O,AB为直径,AD=CD.过点D作DE⊥AB于点E.连结AC交DE于点F.
若sin∠CAB=,DF=5,则BC的长为( )
A.8 B.10 C.12 D.16
8、直角三角形纸片ABC的两直角边长分别为6,8,现将△ABC按图7中所示的方式折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
A. B. C. D.
二、填空题
9、如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是___.
10、如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,
则tan∠BCD的值是___ _____.
11、在△ABC中,∠C=90°,△ABC的面积为6,斜边长为6,则tan A+tan B的值为____.
12、如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处.若AB=4,BC=5,则tan∠AFE的值为____.
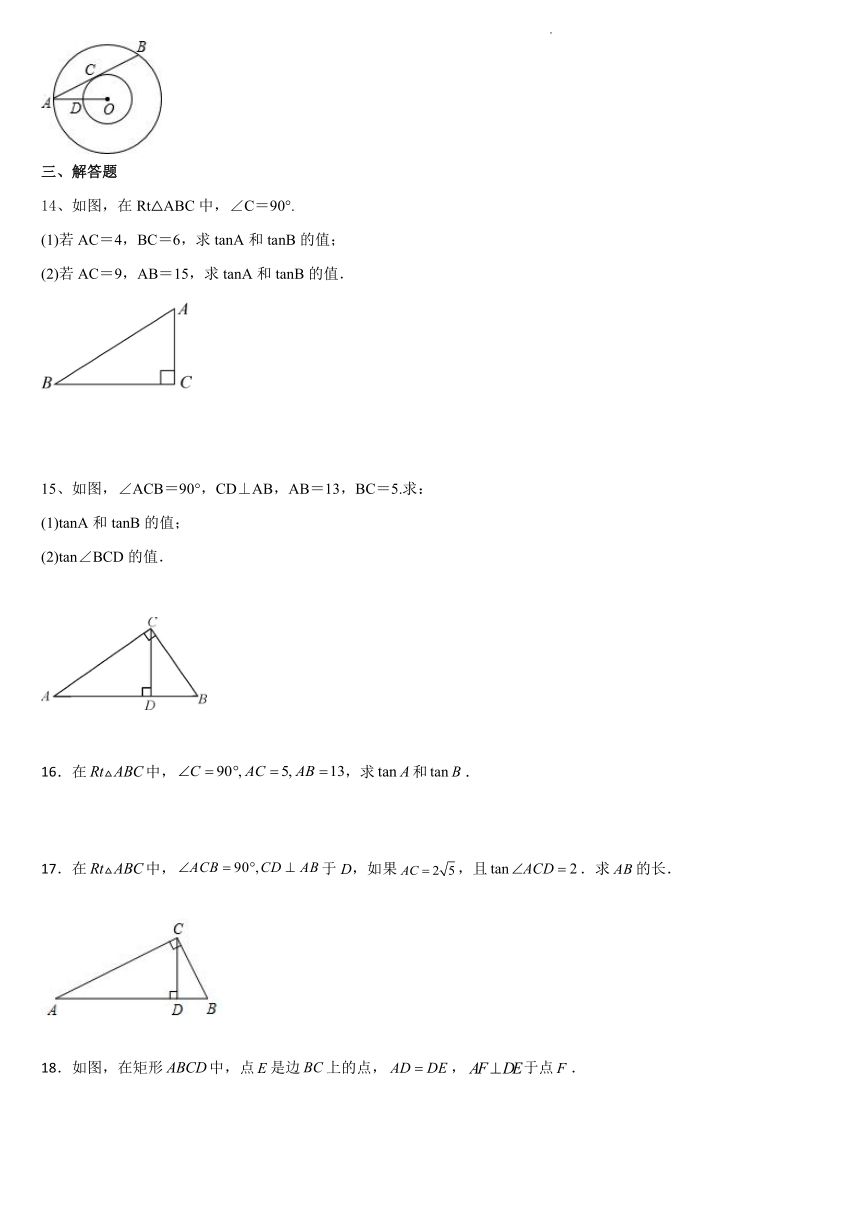
13、如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,大圆的半径OA交小圆于点D,
若OD=3,tan∠OAB=,则AB的长是 .
三、解答题
14、如图,在Rt△ABC中,∠C=90°.
(1)若AC=4,BC=6,求tanA和tanB的值;
(2)若AC=9,AB=15,求tanA和tanB的值.
15、如图,∠ACB=90°,CD⊥AB,AB=13,BC=5.求:
(1)tanA和tanB的值;
(2)tan∠BCD的值.
16.在中,,求和.
17.在中,于D,如果,且.求的长.
18.如图,在矩形中,点是边上的点,,于点.
(1)求证:;
(2)若,,求的长.
7.1正切(1)-苏科版九年级数学下册 培优训练(答案)
一、选择题
1、在Rt△ABC中,若∠C=90°,AC=4,AB=5,则tanB=( A )
A、 B、 C、 D、
2.A
【解析】如图,在中,,
,
设,则,
由勾股定理可得,
.
故选A.
3、如图,已知Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长是( )
A.2 B.8 C.2 D.
【解析】 ∵tanA==,AC=4,∴BC=2.故选A
4、如图,一个斜坡长130 m,坡顶离水平地面的距离为50 m,
那么这个斜坡与水平地面夹角的正切值等于(C )
A. B. C. D.
5、在Rt△ABC中,∠C=90°,AB=5,BC=3,则tanA的值是( )
A. B. C. D.
【解析】 Rt△ABC中,根据勾股定理,得AC===4,
再根据正切函数的定义,得tanA==.故选A.
6、如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=16,tan∠ABD=,则线段AB的长为( )
A. B.10 C.5 D.2
【解析】∵四边形ABCD是菱形,∴AC⊥BD,BO=DO=8,
∵tan∠ABD,∴AO=6,
∴AB10, 故选:B.
7、如图,四边形ABCD内接于⊙O,AB为直径,AD=CD.过点D作DE⊥AB于点E.连结AC交DE于点F.
若sin∠CAB=,DF=5,则BC的长为( )
A.8 B.10 C.12 D.16
【解析】 如答图,连结BD.∵AD=CD,∴∠DAC=∠ACD.∵AB为直径,
∴∠ADB=∠ACB=90°.∴∠DAB+∠ABD=90°.
∵DE⊥AB,∴∠DAB+∠ADE=90°.∴∠ADE=∠ABD.
∵∠ABD=∠ACD,∴∠DAC=∠ADE.
∴AF=DF=5.在Rt△AEF中,sin∠CAB==,∴EF=3,AE=4.
∴DE=3+5=8.由DE2=AE·EB,得BE===16.
∴AB=16+4=20.在Rt△ABC中,sin∠CAB==,∴BC=12.故选C
8、直角三角形纸片ABC的两直角边长分别为6,8,现将△ABC按图7中所示的方式折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
A. B. C. D.
[解析] C 设CE=x,根据折叠的性质,得BE=AE=8-x.在Rt△BCE中,根据勾股定理列出关于x的方程,得x2+62=(8-x)2,解得x=(负值已舍去),即可计算出tan∠CBE=.
二、填空题
9、如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是__ _.
10、如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,
则tan∠BCD的值是___ ______.
11、在△ABC中,∠C=90°,△ABC的面积为6,斜边长为6,则tan A+tan B的值为__3__.
【解】 ∵△ABC的面积为6,∴AC·BC=12.
在Rt△ABC中,∵∠C=90°,AB=6,
∴AC2+BC2=62=36,
∴tan A+tan B=+===3.
12、如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处.若AB=4,BC=5,则tan∠AFE的值为____.
13、如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,大圆的半径OA交小圆于点D,
若OD=3,tan∠OAB=,则AB的长是 .
【解析】连接OC,
∵大圆的弦AB切小圆于点C,∴OC⊥AB,∴AB=2AC,
∵OD=3,∴OC=3,
∵tan∠OAB,∴AC=6,∴AB=12.故答案为:12.
三、解答题
14、如图,在Rt△ABC中,∠C=90°.
(1)若AC=4,BC=6,求tanA和tanB的值;
(2)若AC=9,AB=15,求tanA和tanB的值.
解:(1)tanA===.
tanB===.
(2)BC===12.
tanA===.tanB===.
15、如图,∠ACB=90°,CD⊥AB,AB=13,BC=5.求:
(1)tanA和tanB的值;
(2)tan∠BCD的值.
解:(1)根据勾股定理可知,AC=12. ∴tanA==,tanB==.
(2)tan∠BCD=tanA==.
16.,
【解析】解:如图,
17.5
【解析】解:在中,
,,
∴,
,
,
,
∵,
,
∴在中,.
18(1)见详解;(2)
【解析】(1)证明:∵四边形是矩形,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴;
(2)解:由(1)得:,
∵,
∴,
∵,
∴,
∴,
∴在中,,
设,则有,
∴,即,
解得:,
∴.
一、选择题
1、在Rt△ABC中,若∠C=90°,AC=4,AB=5,则tanB=( )
A、 B、 C、 D、
2.在中,,若,则( )
A. B. C. D.
3、如图,已知Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长是( )
A.2 B.8 C.2 D.
4、如图,一个斜坡长130 m,坡顶离水平地面的距离为50 m,
那么这个斜坡与水平地面夹角的正切值等于( )
A. B. C. D.
5、在Rt△ABC中,∠C=90°,AB=5,BC=3,则tanA的值是( )
A. B. C. D.
6、如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=16,tan∠ABD=,则线段AB的长为( )
A. B.10 C.5 D.2
7、如图,四边形ABCD内接于⊙O,AB为直径,AD=CD.过点D作DE⊥AB于点E.连结AC交DE于点F.
若sin∠CAB=,DF=5,则BC的长为( )
A.8 B.10 C.12 D.16
8、直角三角形纸片ABC的两直角边长分别为6,8,现将△ABC按图7中所示的方式折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
A. B. C. D.
二、填空题
9、如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是___.
10、如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,
则tan∠BCD的值是___ _____.
11、在△ABC中,∠C=90°,△ABC的面积为6,斜边长为6,则tan A+tan B的值为____.
12、如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处.若AB=4,BC=5,则tan∠AFE的值为____.
13、如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,大圆的半径OA交小圆于点D,
若OD=3,tan∠OAB=,则AB的长是 .
三、解答题
14、如图,在Rt△ABC中,∠C=90°.
(1)若AC=4,BC=6,求tanA和tanB的值;
(2)若AC=9,AB=15,求tanA和tanB的值.
15、如图,∠ACB=90°,CD⊥AB,AB=13,BC=5.求:
(1)tanA和tanB的值;
(2)tan∠BCD的值.
16.在中,,求和.
17.在中,于D,如果,且.求的长.
18.如图,在矩形中,点是边上的点,,于点.
(1)求证:;
(2)若,,求的长.
7.1正切(1)-苏科版九年级数学下册 培优训练(答案)
一、选择题
1、在Rt△ABC中,若∠C=90°,AC=4,AB=5,则tanB=( A )
A、 B、 C、 D、
2.A
【解析】如图,在中,,
,
设,则,
由勾股定理可得,
.
故选A.
3、如图,已知Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长是( )
A.2 B.8 C.2 D.
【解析】 ∵tanA==,AC=4,∴BC=2.故选A
4、如图,一个斜坡长130 m,坡顶离水平地面的距离为50 m,
那么这个斜坡与水平地面夹角的正切值等于(C )
A. B. C. D.
5、在Rt△ABC中,∠C=90°,AB=5,BC=3,则tanA的值是( )
A. B. C. D.
【解析】 Rt△ABC中,根据勾股定理,得AC===4,
再根据正切函数的定义,得tanA==.故选A.
6、如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=16,tan∠ABD=,则线段AB的长为( )
A. B.10 C.5 D.2
【解析】∵四边形ABCD是菱形,∴AC⊥BD,BO=DO=8,
∵tan∠ABD,∴AO=6,
∴AB10, 故选:B.
7、如图,四边形ABCD内接于⊙O,AB为直径,AD=CD.过点D作DE⊥AB于点E.连结AC交DE于点F.
若sin∠CAB=,DF=5,则BC的长为( )
A.8 B.10 C.12 D.16
【解析】 如答图,连结BD.∵AD=CD,∴∠DAC=∠ACD.∵AB为直径,
∴∠ADB=∠ACB=90°.∴∠DAB+∠ABD=90°.
∵DE⊥AB,∴∠DAB+∠ADE=90°.∴∠ADE=∠ABD.
∵∠ABD=∠ACD,∴∠DAC=∠ADE.
∴AF=DF=5.在Rt△AEF中,sin∠CAB==,∴EF=3,AE=4.
∴DE=3+5=8.由DE2=AE·EB,得BE===16.
∴AB=16+4=20.在Rt△ABC中,sin∠CAB==,∴BC=12.故选C
8、直角三角形纸片ABC的两直角边长分别为6,8,现将△ABC按图7中所示的方式折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )
A. B. C. D.
[解析] C 设CE=x,根据折叠的性质,得BE=AE=8-x.在Rt△BCE中,根据勾股定理列出关于x的方程,得x2+62=(8-x)2,解得x=(负值已舍去),即可计算出tan∠CBE=.
二、填空题
9、如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是__ _.
10、如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,
则tan∠BCD的值是___ ______.
11、在△ABC中,∠C=90°,△ABC的面积为6,斜边长为6,则tan A+tan B的值为__3__.
【解】 ∵△ABC的面积为6,∴AC·BC=12.
在Rt△ABC中,∵∠C=90°,AB=6,
∴AC2+BC2=62=36,
∴tan A+tan B=+===3.
12、如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处.若AB=4,BC=5,则tan∠AFE的值为____.
13、如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,大圆的半径OA交小圆于点D,
若OD=3,tan∠OAB=,则AB的长是 .
【解析】连接OC,
∵大圆的弦AB切小圆于点C,∴OC⊥AB,∴AB=2AC,
∵OD=3,∴OC=3,
∵tan∠OAB,∴AC=6,∴AB=12.故答案为:12.
三、解答题
14、如图,在Rt△ABC中,∠C=90°.
(1)若AC=4,BC=6,求tanA和tanB的值;
(2)若AC=9,AB=15,求tanA和tanB的值.
解:(1)tanA===.
tanB===.
(2)BC===12.
tanA===.tanB===.
15、如图,∠ACB=90°,CD⊥AB,AB=13,BC=5.求:
(1)tanA和tanB的值;
(2)tan∠BCD的值.
解:(1)根据勾股定理可知,AC=12. ∴tanA==,tanB==.
(2)tan∠BCD=tanA==.
16.,
【解析】解:如图,
17.5
【解析】解:在中,
,,
∴,
,
,
,
∵,
,
∴在中,.
18(1)见详解;(2)
【解析】(1)证明:∵四边形是矩形,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴;
(2)解:由(1)得:,
∵,
∴,
∵,
∴,
∴,
∴在中,,
设,则有,
∴,即,
解得:,
∴.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
