2021-2022学年人教版八年级下册数学18.2.3正方形巩固练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级下册数学18.2.3正方形巩固练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 588.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 21:36:36 | ||
图片预览

文档简介
2021-2022学年八年级下册数学巩固练习(人教版)
18.2.3正方形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在菱形ABCD中,对角线AC、BD交于点O,添加下列条件中的一个,能使菱形ABCD成为正方形的是( )
A. B. C. D.
2.在四边形ABCD中,,若要使该四边形是正方形,则添加的一个条件可以是( )
A. B. C. D.
3.已知四边形ABCD是平行四边形,再从
①,
②,
③,
④四个条件中,
选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①② B.选②③ C.选①③ D.选②④
4.正方形具有而矩形不一定具有的性质是( )
A.四个角都是直角 B.对角线互相平分 C.对角线互相垂直 D.对角线相等
5.正方形的对角线长为a则它的两条对角线的交点到它的一边的距离为( )
A. B. C. D.
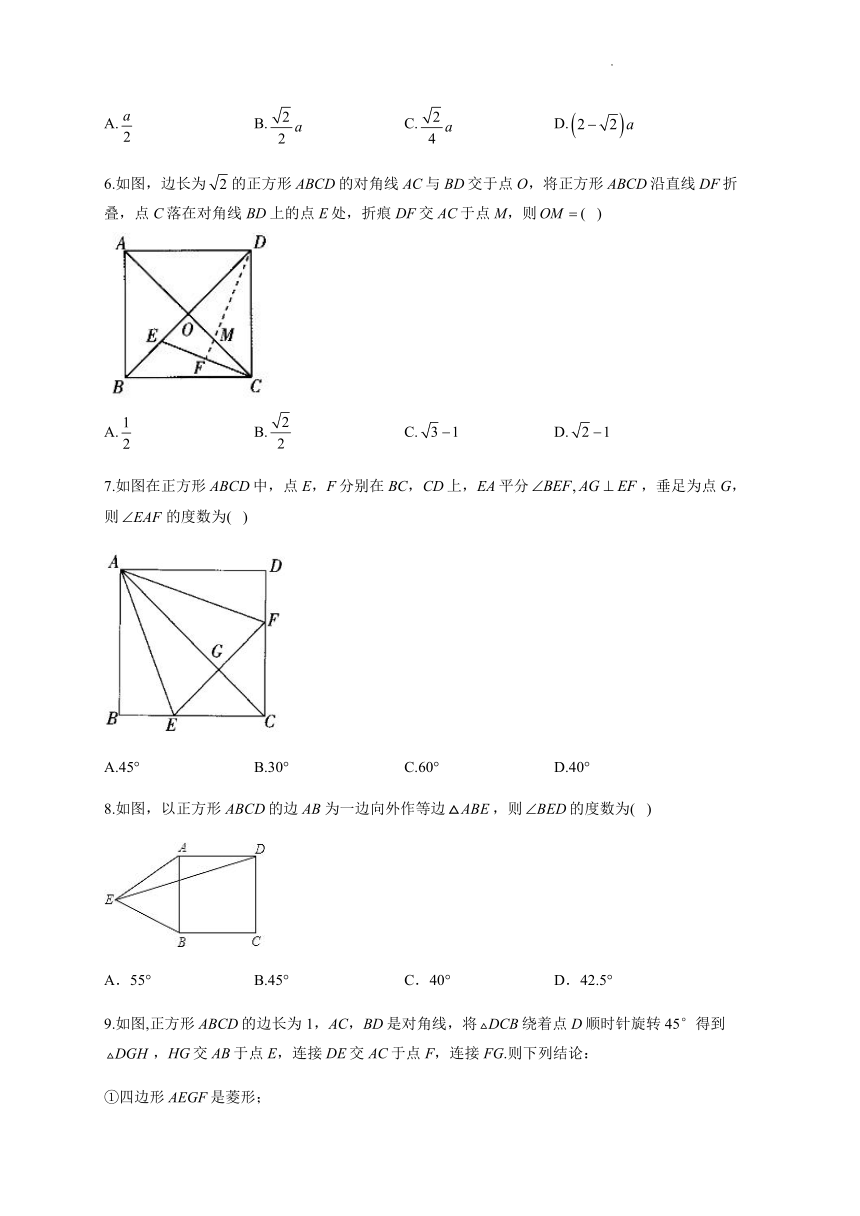
6.如图,边长为的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则( )
A. B. C. D.
7.如图在正方形ABCD中,点E,F分别在BC,CD上,EA平分,垂足为点G,则的度数为( )
A.45° B.30° C.60° D.40°
8.如图,以正方形的边为一边向外作等边,则的度数为( )
A.55° B.45° C.40° D.42.5°
9.如图,正方形ABCD的边长为1,AC,BD是对角线,将绕着点D顺时针旋转45°得到,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形;
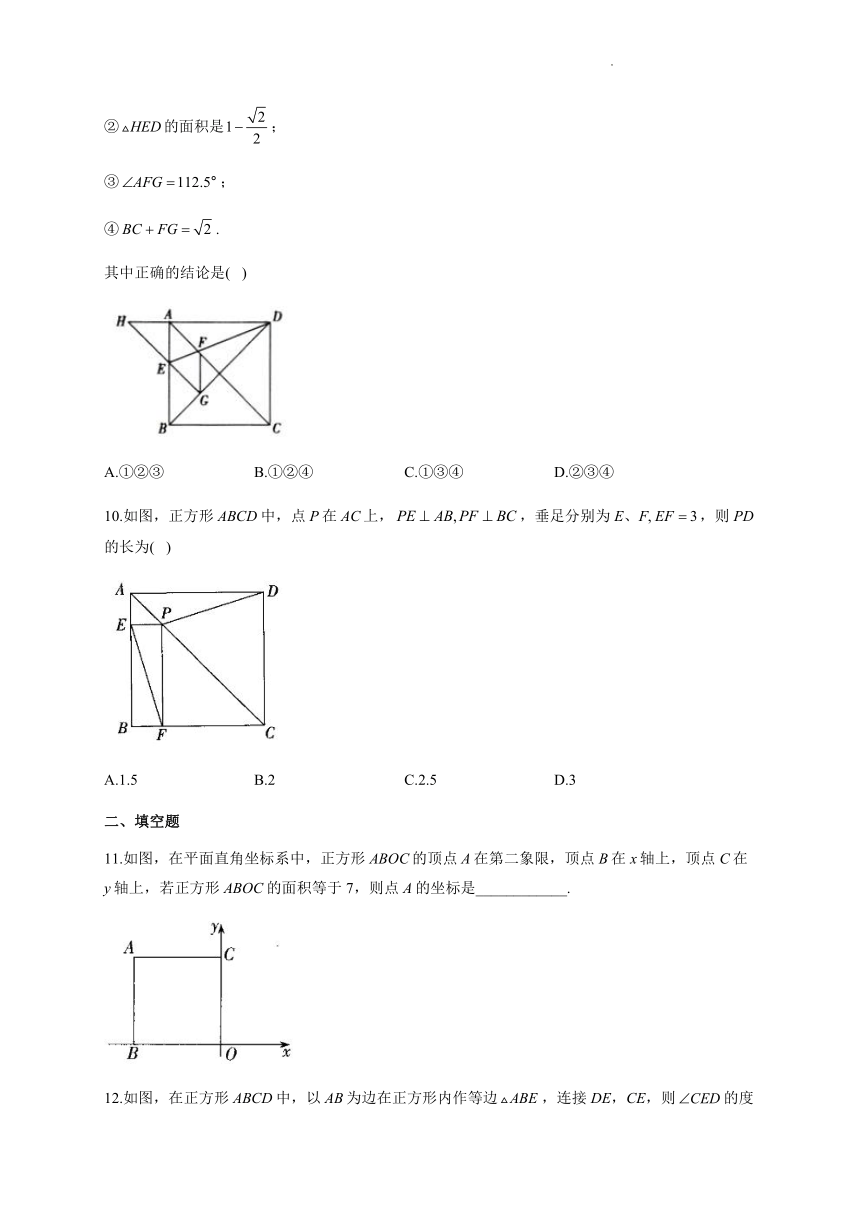
②的面积是;
③;
④.
其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.②③④
10.如图,正方形ABCD中,点P在AC上,,垂足分别为E、F,,则PD的长为( )
A.1.5 B.2 C.2.5 D.3
二、填空题
11.如图,在平面直角坐标系中,正方形ABOC的顶点A在第二象限,顶点B在x轴上,顶点C在y轴上,若正方形ABOC的面积等于7,则点A的坐标是____________.
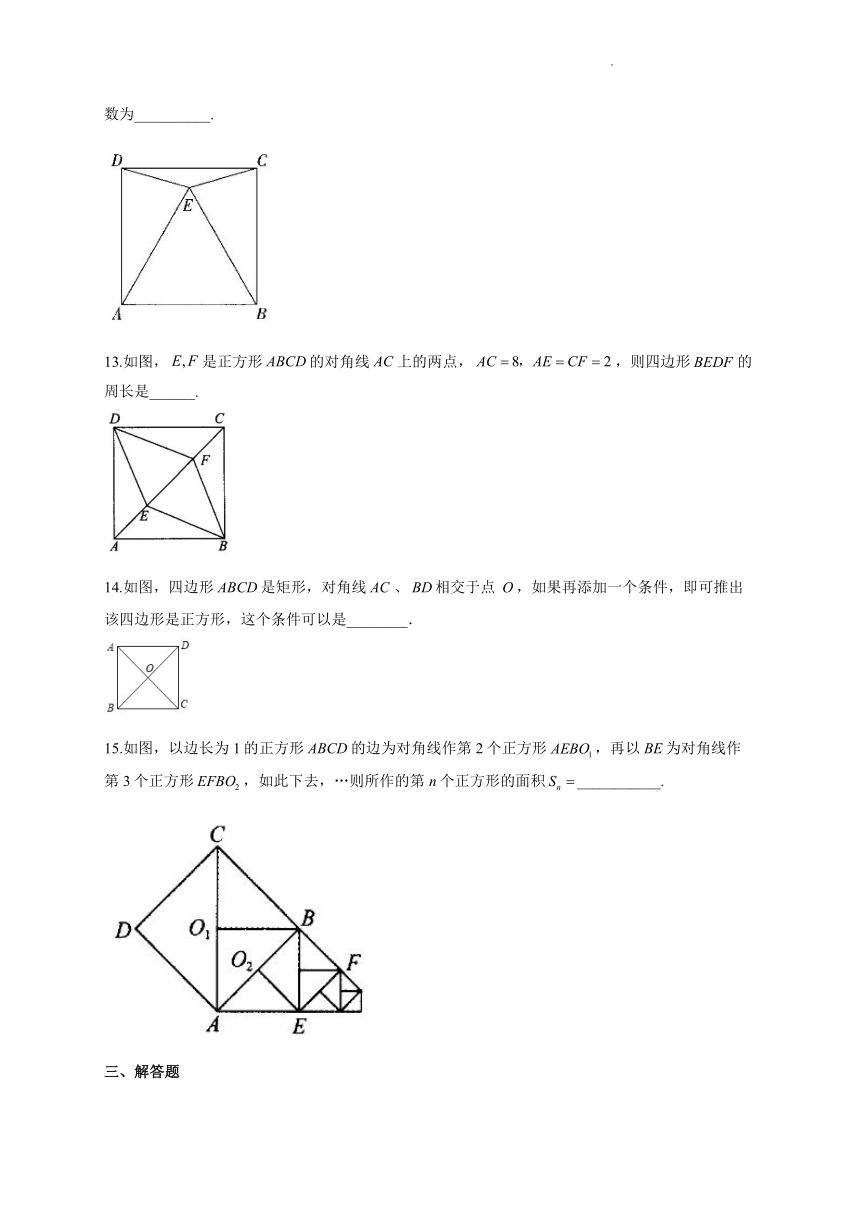
12.如图,在正方形ABCD中,以AB为边在正方形内作等边,连接DE,CE,则的度数为__________.
13.如图,是正方形的对角线上的两点,,则四边形的周长是______.
14.如图,四边形是矩形,对角线、相交于点,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是________.
15.如图,以边长为1的正方形ABCD的边为对角线作第2个正方形,再以BE为对角线作第3个正方形,如此下去,…则所作的第n个正方形的面积___________.
三、解答题
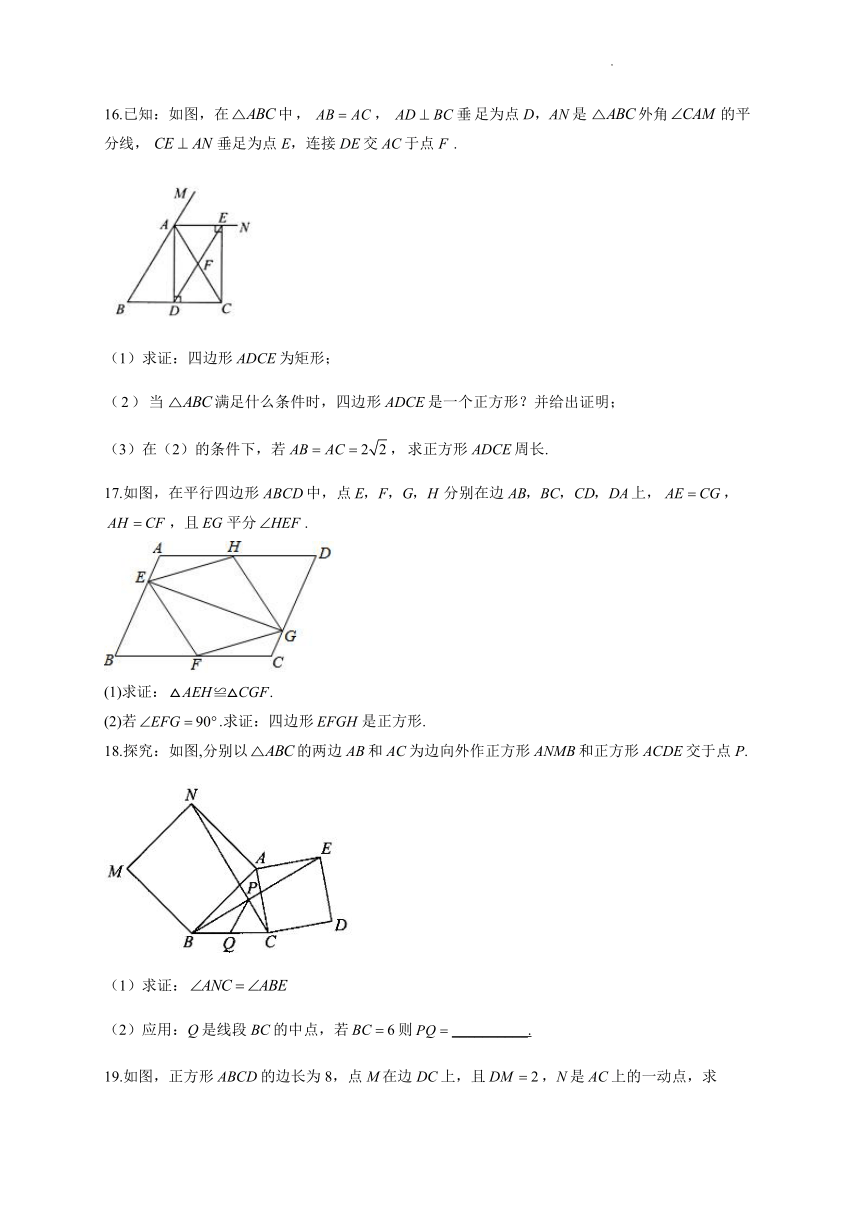
16.已知:如图,在中,,垂足为点D,AN是外角的平分线,垂足为点E,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
(2)当满足什么条件时,四边形ADCE是一个正方形?并给出证明;
(3)在(2)的条件下,若,求正方形ADCE周长.
17.如图,在平行四边形中,点分别在边上,,,且平分.
(1)求证:
(2)若.求证:四边形是正方形.
18.探究:如图,分别以的两边AB和AC为边向外作正方形ANMB和正方形ACDE交于点P.
(1)求证:
(2)应用:Q是线段BC的中点,若则__________.
19.如图,正方形ABCD的边长为8,点M在边DC上,且,N是AC上的一动点,求的最小值.
20.如图,点分别在正方形ABCD的边BC,CD上,且.把绕点A顺时针旋转90°得到.
(1)求证:.
(2)若,求正方形ABCD的边长.
参考答案
1.答案:C
解析:要使菱形成为正方形,只要菱形满足以下条件之一即可:(1)有一个内角是直角;(2)对角线相等,即或.故选C.
2.答案:D
解析:,四边形ABCD是矩形,当时,四边形ABCD是正方形,故选D.
3.答案:B
解析:由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,故选②③不能得出四边形ABCD是正方形.故选B.
4.答案:C
解析:A.正方形和矩形的四个角都是直角,故本选项不符合题意;B.正方形和矩形的对角线都互相平分,故本选项不符合题意;C.正方形的对角线互相垂直,矩形的对角线不一定互相垂直,故本选项符合题意;D.正方形和矩形的对角线都相等,故本选项不符合题意.故选C.
5.答案:C
6.答案:D
解析:本题考查全等三角形的判定、图形折叠的性质.
四边形ABCD是边长为的正方形,,.
由折叠的性质知:,,,.
.在与中,
,
,故选D.
7.答案:A
解析:在正方形ABCD中,,
,
,
EA平分,,
.
在与中,,
,
,
,
故选A.
8.答案:B
9.答案:B
解析:四边形ABCD是正方形,,,.
由旋转得到,,
在和中,,,,
同理,,四边形AEGF是菱形,①正确,,③错误.
根据题意可求得,
在等腰直角三角形EGB中,可求得,故,所以,即可得的面积是,②正确.
由①的证明过程可得,所以,即可得,④正确.
综上,正确的结论为①②④.故选B.
10.答案:D
解析:如图,连接PB,
在正方形ABCD中,,又,.,四边形BFPE是矩形,,故选D.
11.答案:
解析:正方形ABOC的面积等于7,正方形ABOC的边长为,正方形ABOC的顶点A在第二象限,点A的坐标是.
12.答案:150°
解析:四边形ABCD是正方形,
.
是等边三角形,
,
,
,
.
13.答案:
解析:本题考查正方形的性质、菱形的判定及性质、勾股定理.如图,连接交于点O,在正方形中,,,,,∴四边形是菱形.又与互相垂直平分,,在中,由勾股定理得四边形的周长为
14.答案:
解析:∵四边形是矩形,
∴当时,四边形是正方形,
故答案为:
15.答案:
解析:第1个正方形的边长为1,面积;第2个正方形的边长为,面积;第3个正方形的边长为,面积;第4个正方形的边长为,面积,…,则第n个正方形的面积.
16.答案:(1),,
,AN是外角的平分线,
.与互为补角,,
,
,,
,
四边形ADCE为矩形.
(2)当时,四边形ADCE是一个正方形.证明如下:
且,.
,.
,.
四边形ADCE为矩形,四边形ADCE为正方形.
(3)由勾股定理,得.
,即,,
正方形ADCE周长.
17.答案:(1)∵四边形是平行四边形
∴
(2) ∵四边形是平行四边形
又
∴四边形为平行四边形
∵EG平分
又∵
∴平行四边形是正方形
18.答案:(1)四边形ANMB和ACDE是正方形,,.
,,
.
在和中,
,
.
(2)设AB与NC相交于点O.四边形NABM是正方形,
.,,
,,
Q为BC中点,,.
19.答案:如答图,连接BN,BD.
因为正方形是轴对称图形,点B与点D关于直线AC对称,
所以由对称性可知,
所以.
连接BM交AC于点P.
因为N为AC上的一动点,
所以由三角形两边之和大于第三边知,当点N运动到点P时,取得最小值,即BM的长.
因为四边形ABCD为正方形,
所以,,,
所以,所以(负值已舍去),
即的最小值为10.
20.答案:(1)证明:如图,由旋转知,
.
。,
.
在和中
(2)由(1)知即
.
.
设正方形的边长为a,
则
在中,
.
解得(舍去).
故正方形的边长为6.
18.2.3正方形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在菱形ABCD中,对角线AC、BD交于点O,添加下列条件中的一个,能使菱形ABCD成为正方形的是( )
A. B. C. D.
2.在四边形ABCD中,,若要使该四边形是正方形,则添加的一个条件可以是( )
A. B. C. D.
3.已知四边形ABCD是平行四边形,再从
①,
②,
③,
④四个条件中,
选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①② B.选②③ C.选①③ D.选②④
4.正方形具有而矩形不一定具有的性质是( )
A.四个角都是直角 B.对角线互相平分 C.对角线互相垂直 D.对角线相等
5.正方形的对角线长为a则它的两条对角线的交点到它的一边的距离为( )
A. B. C. D.
6.如图,边长为的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则( )
A. B. C. D.
7.如图在正方形ABCD中,点E,F分别在BC,CD上,EA平分,垂足为点G,则的度数为( )
A.45° B.30° C.60° D.40°
8.如图,以正方形的边为一边向外作等边,则的度数为( )
A.55° B.45° C.40° D.42.5°
9.如图,正方形ABCD的边长为1,AC,BD是对角线,将绕着点D顺时针旋转45°得到,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形;
②的面积是;
③;
④.
其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.②③④
10.如图,正方形ABCD中,点P在AC上,,垂足分别为E、F,,则PD的长为( )
A.1.5 B.2 C.2.5 D.3
二、填空题
11.如图,在平面直角坐标系中,正方形ABOC的顶点A在第二象限,顶点B在x轴上,顶点C在y轴上,若正方形ABOC的面积等于7,则点A的坐标是____________.
12.如图,在正方形ABCD中,以AB为边在正方形内作等边,连接DE,CE,则的度数为__________.
13.如图,是正方形的对角线上的两点,,则四边形的周长是______.
14.如图,四边形是矩形,对角线、相交于点,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是________.
15.如图,以边长为1的正方形ABCD的边为对角线作第2个正方形,再以BE为对角线作第3个正方形,如此下去,…则所作的第n个正方形的面积___________.
三、解答题
16.已知:如图,在中,,垂足为点D,AN是外角的平分线,垂足为点E,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
(2)当满足什么条件时,四边形ADCE是一个正方形?并给出证明;
(3)在(2)的条件下,若,求正方形ADCE周长.
17.如图,在平行四边形中,点分别在边上,,,且平分.
(1)求证:
(2)若.求证:四边形是正方形.
18.探究:如图,分别以的两边AB和AC为边向外作正方形ANMB和正方形ACDE交于点P.
(1)求证:
(2)应用:Q是线段BC的中点,若则__________.
19.如图,正方形ABCD的边长为8,点M在边DC上,且,N是AC上的一动点,求的最小值.
20.如图,点分别在正方形ABCD的边BC,CD上,且.把绕点A顺时针旋转90°得到.
(1)求证:.
(2)若,求正方形ABCD的边长.
参考答案
1.答案:C
解析:要使菱形成为正方形,只要菱形满足以下条件之一即可:(1)有一个内角是直角;(2)对角线相等,即或.故选C.
2.答案:D
解析:,四边形ABCD是矩形,当时,四边形ABCD是正方形,故选D.
3.答案:B
解析:由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,故选②③不能得出四边形ABCD是正方形.故选B.
4.答案:C
解析:A.正方形和矩形的四个角都是直角,故本选项不符合题意;B.正方形和矩形的对角线都互相平分,故本选项不符合题意;C.正方形的对角线互相垂直,矩形的对角线不一定互相垂直,故本选项符合题意;D.正方形和矩形的对角线都相等,故本选项不符合题意.故选C.
5.答案:C
6.答案:D
解析:本题考查全等三角形的判定、图形折叠的性质.
四边形ABCD是边长为的正方形,,.
由折叠的性质知:,,,.
.在与中,
,
,故选D.
7.答案:A
解析:在正方形ABCD中,,
,
,
EA平分,,
.
在与中,,
,
,
,
故选A.
8.答案:B
9.答案:B
解析:四边形ABCD是正方形,,,.
由旋转得到,,
在和中,,,,
同理,,四边形AEGF是菱形,①正确,,③错误.
根据题意可求得,
在等腰直角三角形EGB中,可求得,故,所以,即可得的面积是,②正确.
由①的证明过程可得,所以,即可得,④正确.
综上,正确的结论为①②④.故选B.
10.答案:D
解析:如图,连接PB,
在正方形ABCD中,,又,.,四边形BFPE是矩形,,故选D.
11.答案:
解析:正方形ABOC的面积等于7,正方形ABOC的边长为,正方形ABOC的顶点A在第二象限,点A的坐标是.
12.答案:150°
解析:四边形ABCD是正方形,
.
是等边三角形,
,
,
,
.
13.答案:
解析:本题考查正方形的性质、菱形的判定及性质、勾股定理.如图,连接交于点O,在正方形中,,,,,∴四边形是菱形.又与互相垂直平分,,在中,由勾股定理得四边形的周长为
14.答案:
解析:∵四边形是矩形,
∴当时,四边形是正方形,
故答案为:
15.答案:
解析:第1个正方形的边长为1,面积;第2个正方形的边长为,面积;第3个正方形的边长为,面积;第4个正方形的边长为,面积,…,则第n个正方形的面积.
16.答案:(1),,
,AN是外角的平分线,
.与互为补角,,
,
,,
,
四边形ADCE为矩形.
(2)当时,四边形ADCE是一个正方形.证明如下:
且,.
,.
,.
四边形ADCE为矩形,四边形ADCE为正方形.
(3)由勾股定理,得.
,即,,
正方形ADCE周长.
17.答案:(1)∵四边形是平行四边形
∴
(2) ∵四边形是平行四边形
又
∴四边形为平行四边形
∵EG平分
又∵
∴平行四边形是正方形
18.答案:(1)四边形ANMB和ACDE是正方形,,.
,,
.
在和中,
,
.
(2)设AB与NC相交于点O.四边形NABM是正方形,
.,,
,,
Q为BC中点,,.
19.答案:如答图,连接BN,BD.
因为正方形是轴对称图形,点B与点D关于直线AC对称,
所以由对称性可知,
所以.
连接BM交AC于点P.
因为N为AC上的一动点,
所以由三角形两边之和大于第三边知,当点N运动到点P时,取得最小值,即BM的长.
因为四边形ABCD为正方形,
所以,,,
所以,所以(负值已舍去),
即的最小值为10.
20.答案:(1)证明:如图,由旋转知,
.
。,
.
在和中
(2)由(1)知即
.
.
设正方形的边长为a,
则
在中,
.
解得(舍去).
故正方形的边长为6.
