2021-2022学年北师大数学八年级下册1.4角平分线+课后训练A(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大数学八年级下册1.4角平分线+课后训练A(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 458.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 21:36:37 | ||
图片预览



文档简介
北师大数学八年级下册第一章 三角形的证明 1.3角平分线 课后训练A(含答案)
姓名:___________班级:___________
一、单选题
1.下列命题是真命题的是( )
A.同旁内角互补 B.任意一个等腰三角形一定是钝角三角形
C.两边及一角对应相等的两个三角形全等 D.角平分线上的点到角两边的距离相等
2.如图,已知,求作射线,使平分,那么作法的合理顺序是( )
①作射线;②在射线和上分别截取、,使;③分别以、为圆心,大于的长为半径在内作弧,两弧交于点.
A.①②③ B.②①③ C.②③① D.③①②
3.如图,的三边,,长分别是,,,其三条角平分线将分为三个三角形,则::等于( )
A.:: B.::
C.:: D.::
4.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
5.△ABC的两条角平分线AD,BE相交于点F,下列结论一定正确的是( )
A.BD = DC B.BE⊥AC
C.FA = FB D.点F到三角形三边的距离都相等
6.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A.15 B.30 C.45 D.60
7.如图,在△ABC中,BC=10,CD是∠ACB的平分线.若P,Q分别是CD和AC上的动点,且△ABC的面积为24,则PA+PQ的最小值是( )
A. B.4 C. D.5
8.如图,∠BAC=30°,AD平分∠BAC,DF⊥AB交AB于F,DE⊥DF交AC于E,若AE=8,则DF等于( )
A.5 B.4 C.3 D.2
9.如图,,BP和CP分别平分∠ABC和∠BCD,AD过点P,且与AB垂直.若,,则BCP的面积为( )
A.16 B.20 C.40 D.80
10.如图,钝角三角形△ABC的面积是20,最长边BC=10,CD平分∠ACB,点P,Q分别是CD,AC上的动点,则AP+PQ的最小值为( )
A.2 B.3 C.4 D.5
11.如图,在中,,,以点为圆心,适当长为半径画弧,分别交,于点和,再分别以点和为圆心,大于的长为半径画弧,两弧交于点,作射线交于点则下列结论:①是的角平分线;②点在线段的垂直平分线上;③;④::;⑤,其中正确结论的个数是( )
A.个 B.个 C.个 D.个
12.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交B于点D,则下列说法中正确的个数是( )
①是的平分线;
②;
③点D在AB的中垂线上;
④::.
A. B. C. D.
二、填空题
13.如图,已知的周长是22,PB、PC分别平分和,于D,且,的面积是________.
14.如图,在中,,平分,,点到的距离为5.6,则___.
15.如图,在中,是边上的高,平分,交于点E,且EFBC,垂足为点F,,则EF的值为___________.
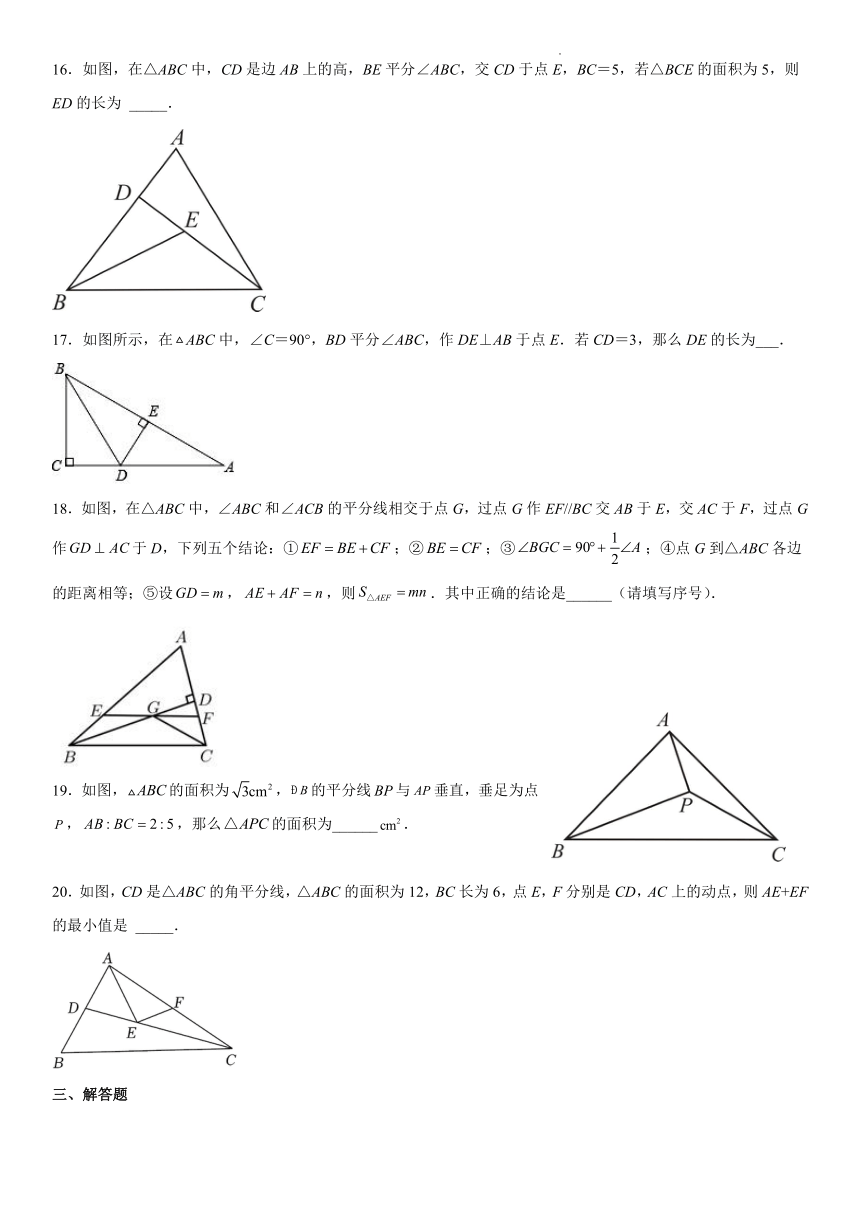
16.如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=5,若△BCE的面积为5,则ED的长为 _____.
17.如图所示,在ABC中,∠C=90°,BD平分∠ABC,作DE⊥AB于点E.若CD=3,那么DE的长为___.
18.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF//BC交AB于E,交AC于F,过点G作于D,下列五个结论:①;②;③;④点G到△ABC各边的距离相等;⑤设,,则.其中正确的结论是______(请填写序号).
19.如图,的面积为,的平分线与垂直,垂足为点,,那么的面积为______.
20.如图,CD是△ABC的角平分线,△ABC的面积为12,BC长为6,点E,F分别是CD,AC上的动点,则AE+EF的最小值是 _____.
三、解答题
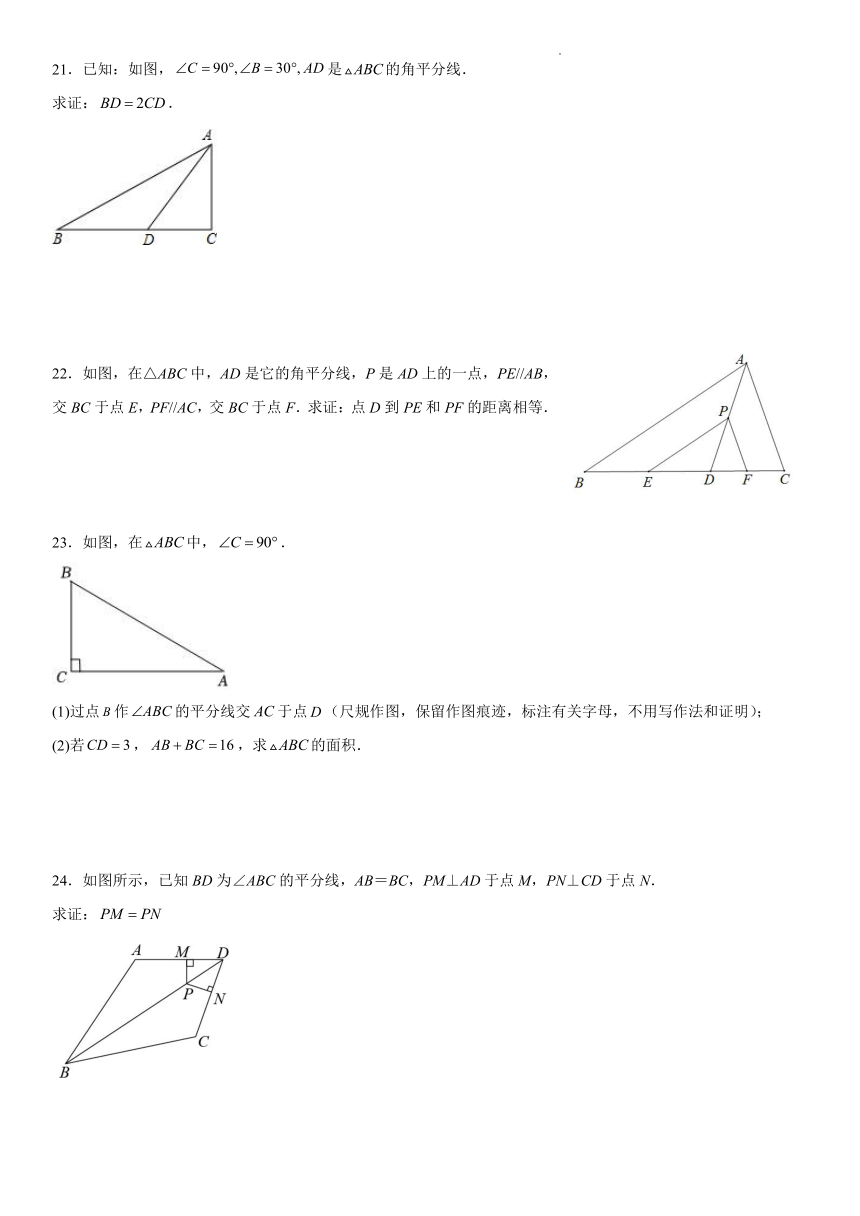
21.已知:如图,是的角平分线.
求证:.
22.如图,在△ABC中,AD是它的角平分线,P是AD上的一点,PE//AB,交BC于点E,PF//AC,交BC于点F.求证:点D到PE和PF的距离相等.
23.如图,在中,.
(1)过点作的平分线交于点(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);
(2)若,,求的面积.
24.如图所示,已知BD为∠ABC的平分线,AB=BC,PM⊥AD于点M,PN⊥CD于点N.
求证:
25.如图,在梯形ABCD中,∠A=∠B=90°,点E为AB的中点,DE平分∠ADC.
(1)求证:CE平分∠BCD;
(2)求证:AD+BC=CD.
26.在中,,,于D,过C点引射线交延长线于F点.过B点作于E点、分别交、于点G,H.
(1)求证:;
(2)若;
①判断是否是的角平分线,并说明理由;
②说明.
27.如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证:DE=DF;
(2)若AB=5,BC=8,求DE的长.
参考答案:
1.D 2.C 3.C 4.C 5.D 6.B 7.C 8.B 9.B 10.C 11.D 12.D
13.33
14.
15.4
16.2
17.3
18.①③④
19.
20.4
21.证明:如图,过点D作DE⊥AB于点E,
∵AD平分,DE⊥AB,,
∴DE=DC,
∵在直角三角形BED中,,
∴,
∴.
22.证明:∵PE∥AB,PF∥AC,
∴∠EPD=∠BAD,∠DPF=∠CAD,
∵△ABC中,AD是它的角平分线,
∴∠BAD=∠CAD,
∴∠EPD=∠DPF,
即PD平分∠EPF,
∴D到PE的距离与D到PF的距离相等.
23.(1)∠ABC的平分线如图所示.
(2)作DH⊥AB于H.
∵BD平分∠ABC,DC⊥BC,DH⊥AB,
∴CD=DH=3,
∴△ABC的面积=S△BCD+S△ABD=BC CD+AB DH=×3BC+×3AB=×3(BC+AB)=×3×16=24.
24.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∴BD平分∠ADC,
∵PM⊥AD,PN⊥CD,
∴PM=PN.
25.(1)证明:如图,作EM⊥CD垂足为M,
∵ED平分∠ADM,EA⊥AD,EM⊥CD,
∴AE=EM,
∵AE=EB,
∴EM=EB,
∵EB⊥BC,EM⊥CD,
∴EC平分∠BCD.
(2)证明:由(1)可知:AE=EM=EB,
在Rt△DEA和Rt△DEM中,
,
∴Rt△DEA≌Rt△DEM(HL),
∴DA=DM,
同理可证:Rt△BEC≌Rt△BMC(HL),
∴CB=CM,
∴CD=DM+MC=AD+BC.
26.(1)证明:∵BE⊥CF于E点,
∴∠BEC=90°,
∴∠BAC=90°=∠BEC
∵∠ABH+∠BHA=90°,∠ACF+∠CHE=90°,∠BHA=∠CHE,
∴∠ABH=∠ACF
在△ABH和△ACF中
∵
∴△ABH≌△ACF(AAS).
(2)解:①BE是CBF是角平分线.
理由如下:∵AG=AH,
∴∠AGH=∠AHG,
∵∠AGH=∠BGD,
∴∠AHG=∠BGD
∵AD⊥BC于D点,
∴∠GBD+∠BGD=90°,
∵∠BAC=90°,
∴∠ABH+∠AHB=90°,
∴∠GBD=∠ABH,
∴BE是△CBF是角平分线.
②证明:∵△ABH≌△ACF,
∴BH=CF,
∵BE是△CBF是角平分线,
∴,
在△BCE和△BFE中
∵
∴△BCE≌△BFE,
∴EF=CE=,
∴BH=2CE.
27.(1)证明:如图,连接AD,
∵∠B=∠C,
∴AB=AC,
∵D是BC的中点,
∴AD平分∠BAC,
∵DE⊥AB,DF⊥AC,
∴DE=DF;
(2)解:∵AB=AC,
∵D是BC的中点,
∴AD⊥BC,BD=CD=BC=4,
∴AD===3,
∴S△ABD=AB DE=BD AD,
∴5DE=4×3,
∴DE=.
答案第1页,共2页
姓名:___________班级:___________
一、单选题
1.下列命题是真命题的是( )
A.同旁内角互补 B.任意一个等腰三角形一定是钝角三角形
C.两边及一角对应相等的两个三角形全等 D.角平分线上的点到角两边的距离相等
2.如图,已知,求作射线,使平分,那么作法的合理顺序是( )
①作射线;②在射线和上分别截取、,使;③分别以、为圆心,大于的长为半径在内作弧,两弧交于点.
A.①②③ B.②①③ C.②③① D.③①②
3.如图,的三边,,长分别是,,,其三条角平分线将分为三个三角形,则::等于( )
A.:: B.::
C.:: D.::
4.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
5.△ABC的两条角平分线AD,BE相交于点F,下列结论一定正确的是( )
A.BD = DC B.BE⊥AC
C.FA = FB D.点F到三角形三边的距离都相等
6.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A.15 B.30 C.45 D.60
7.如图,在△ABC中,BC=10,CD是∠ACB的平分线.若P,Q分别是CD和AC上的动点,且△ABC的面积为24,则PA+PQ的最小值是( )
A. B.4 C. D.5
8.如图,∠BAC=30°,AD平分∠BAC,DF⊥AB交AB于F,DE⊥DF交AC于E,若AE=8,则DF等于( )
A.5 B.4 C.3 D.2
9.如图,,BP和CP分别平分∠ABC和∠BCD,AD过点P,且与AB垂直.若,,则BCP的面积为( )
A.16 B.20 C.40 D.80
10.如图,钝角三角形△ABC的面积是20,最长边BC=10,CD平分∠ACB,点P,Q分别是CD,AC上的动点,则AP+PQ的最小值为( )
A.2 B.3 C.4 D.5
11.如图,在中,,,以点为圆心,适当长为半径画弧,分别交,于点和,再分别以点和为圆心,大于的长为半径画弧,两弧交于点,作射线交于点则下列结论:①是的角平分线;②点在线段的垂直平分线上;③;④::;⑤,其中正确结论的个数是( )
A.个 B.个 C.个 D.个
12.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交B于点D,则下列说法中正确的个数是( )
①是的平分线;
②;
③点D在AB的中垂线上;
④::.
A. B. C. D.
二、填空题
13.如图,已知的周长是22,PB、PC分别平分和,于D,且,的面积是________.
14.如图,在中,,平分,,点到的距离为5.6,则___.
15.如图,在中,是边上的高,平分,交于点E,且EFBC,垂足为点F,,则EF的值为___________.
16.如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=5,若△BCE的面积为5,则ED的长为 _____.
17.如图所示,在ABC中,∠C=90°,BD平分∠ABC,作DE⊥AB于点E.若CD=3,那么DE的长为___.
18.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF//BC交AB于E,交AC于F,过点G作于D,下列五个结论:①;②;③;④点G到△ABC各边的距离相等;⑤设,,则.其中正确的结论是______(请填写序号).
19.如图,的面积为,的平分线与垂直,垂足为点,,那么的面积为______.
20.如图,CD是△ABC的角平分线,△ABC的面积为12,BC长为6,点E,F分别是CD,AC上的动点,则AE+EF的最小值是 _____.
三、解答题
21.已知:如图,是的角平分线.
求证:.
22.如图,在△ABC中,AD是它的角平分线,P是AD上的一点,PE//AB,交BC于点E,PF//AC,交BC于点F.求证:点D到PE和PF的距离相等.
23.如图,在中,.
(1)过点作的平分线交于点(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);
(2)若,,求的面积.
24.如图所示,已知BD为∠ABC的平分线,AB=BC,PM⊥AD于点M,PN⊥CD于点N.
求证:
25.如图,在梯形ABCD中,∠A=∠B=90°,点E为AB的中点,DE平分∠ADC.
(1)求证:CE平分∠BCD;
(2)求证:AD+BC=CD.
26.在中,,,于D,过C点引射线交延长线于F点.过B点作于E点、分别交、于点G,H.
(1)求证:;
(2)若;
①判断是否是的角平分线,并说明理由;
②说明.
27.如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证:DE=DF;
(2)若AB=5,BC=8,求DE的长.
参考答案:
1.D 2.C 3.C 4.C 5.D 6.B 7.C 8.B 9.B 10.C 11.D 12.D
13.33
14.
15.4
16.2
17.3
18.①③④
19.
20.4
21.证明:如图,过点D作DE⊥AB于点E,
∵AD平分,DE⊥AB,,
∴DE=DC,
∵在直角三角形BED中,,
∴,
∴.
22.证明:∵PE∥AB,PF∥AC,
∴∠EPD=∠BAD,∠DPF=∠CAD,
∵△ABC中,AD是它的角平分线,
∴∠BAD=∠CAD,
∴∠EPD=∠DPF,
即PD平分∠EPF,
∴D到PE的距离与D到PF的距离相等.
23.(1)∠ABC的平分线如图所示.
(2)作DH⊥AB于H.
∵BD平分∠ABC,DC⊥BC,DH⊥AB,
∴CD=DH=3,
∴△ABC的面积=S△BCD+S△ABD=BC CD+AB DH=×3BC+×3AB=×3(BC+AB)=×3×16=24.
24.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∴BD平分∠ADC,
∵PM⊥AD,PN⊥CD,
∴PM=PN.
25.(1)证明:如图,作EM⊥CD垂足为M,
∵ED平分∠ADM,EA⊥AD,EM⊥CD,
∴AE=EM,
∵AE=EB,
∴EM=EB,
∵EB⊥BC,EM⊥CD,
∴EC平分∠BCD.
(2)证明:由(1)可知:AE=EM=EB,
在Rt△DEA和Rt△DEM中,
,
∴Rt△DEA≌Rt△DEM(HL),
∴DA=DM,
同理可证:Rt△BEC≌Rt△BMC(HL),
∴CB=CM,
∴CD=DM+MC=AD+BC.
26.(1)证明:∵BE⊥CF于E点,
∴∠BEC=90°,
∴∠BAC=90°=∠BEC
∵∠ABH+∠BHA=90°,∠ACF+∠CHE=90°,∠BHA=∠CHE,
∴∠ABH=∠ACF
在△ABH和△ACF中
∵
∴△ABH≌△ACF(AAS).
(2)解:①BE是CBF是角平分线.
理由如下:∵AG=AH,
∴∠AGH=∠AHG,
∵∠AGH=∠BGD,
∴∠AHG=∠BGD
∵AD⊥BC于D点,
∴∠GBD+∠BGD=90°,
∵∠BAC=90°,
∴∠ABH+∠AHB=90°,
∴∠GBD=∠ABH,
∴BE是△CBF是角平分线.
②证明:∵△ABH≌△ACF,
∴BH=CF,
∵BE是△CBF是角平分线,
∴,
在△BCE和△BFE中
∵
∴△BCE≌△BFE,
∴EF=CE=,
∴BH=2CE.
27.(1)证明:如图,连接AD,
∵∠B=∠C,
∴AB=AC,
∵D是BC的中点,
∴AD平分∠BAC,
∵DE⊥AB,DF⊥AC,
∴DE=DF;
(2)解:∵AB=AC,
∵D是BC的中点,
∴AD⊥BC,BD=CD=BC=4,
∴AD===3,
∴S△ABD=AB DE=BD AD,
∴5DE=4×3,
∴DE=.
答案第1页,共2页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
