2021-2022学年人教版八年级下册数学18.2.1矩形巩固练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级下册数学18.2.1矩形巩固练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 537.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 21:39:56 | ||
图片预览

文档简介
2021-2022学年八年级下册数学巩固练习(人教版)
18.2.1矩形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列关于矩形的说法中正确的是( )
A.矩形的对角线互相垂直且平分 B.矩形的对角线相等且互相平分
C.对角线相等的四边形是矩形 D.对角线互相平分的四边形是矩形
2.如图,四边形ABCD的对角线相交于点O,且互相平分,若添加下列条件中的一个,不能判定四边形ABCD为矩形的是( )
A. B. C. D.
3.已知平行四边形ABCD中,下列条件:
①;
②;
③;
④AC平分,
其中能说明平行四边形ABCD是矩形的是( )
A.① B.② C.③ D.④
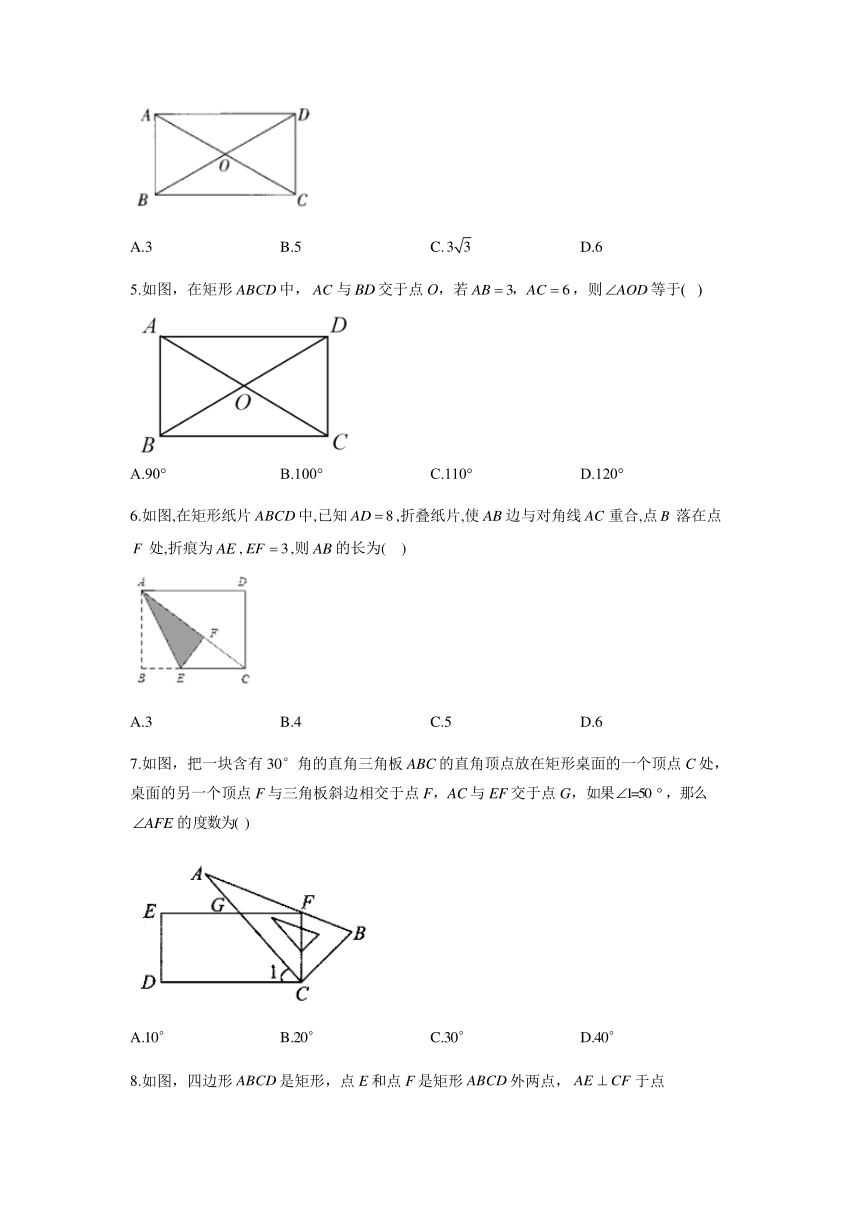
4.如图,矩形ABCD中,,则BD的长是( )
A.3 B.5 C. D.6
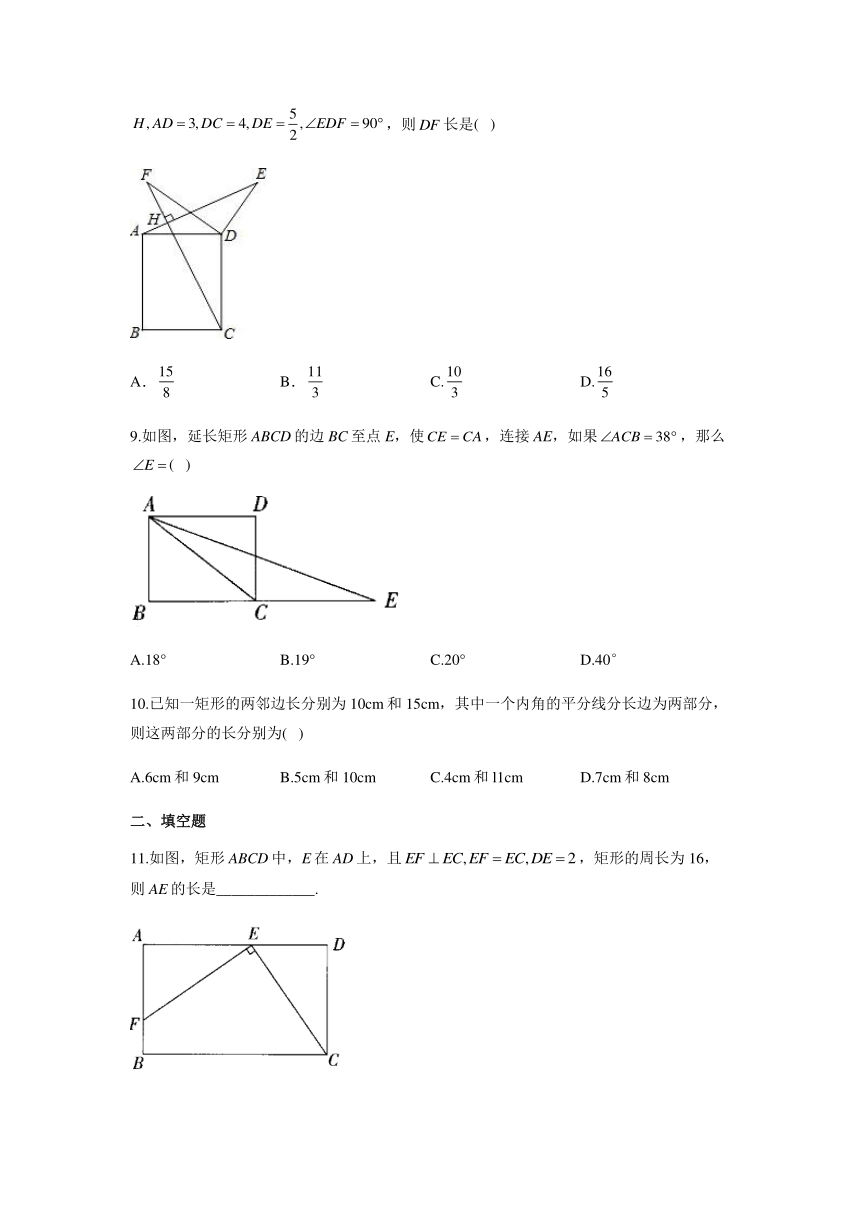
5.如图,在矩形中,与交于点O,若,则等于( )
A.90° B.100° C.110° D.120°
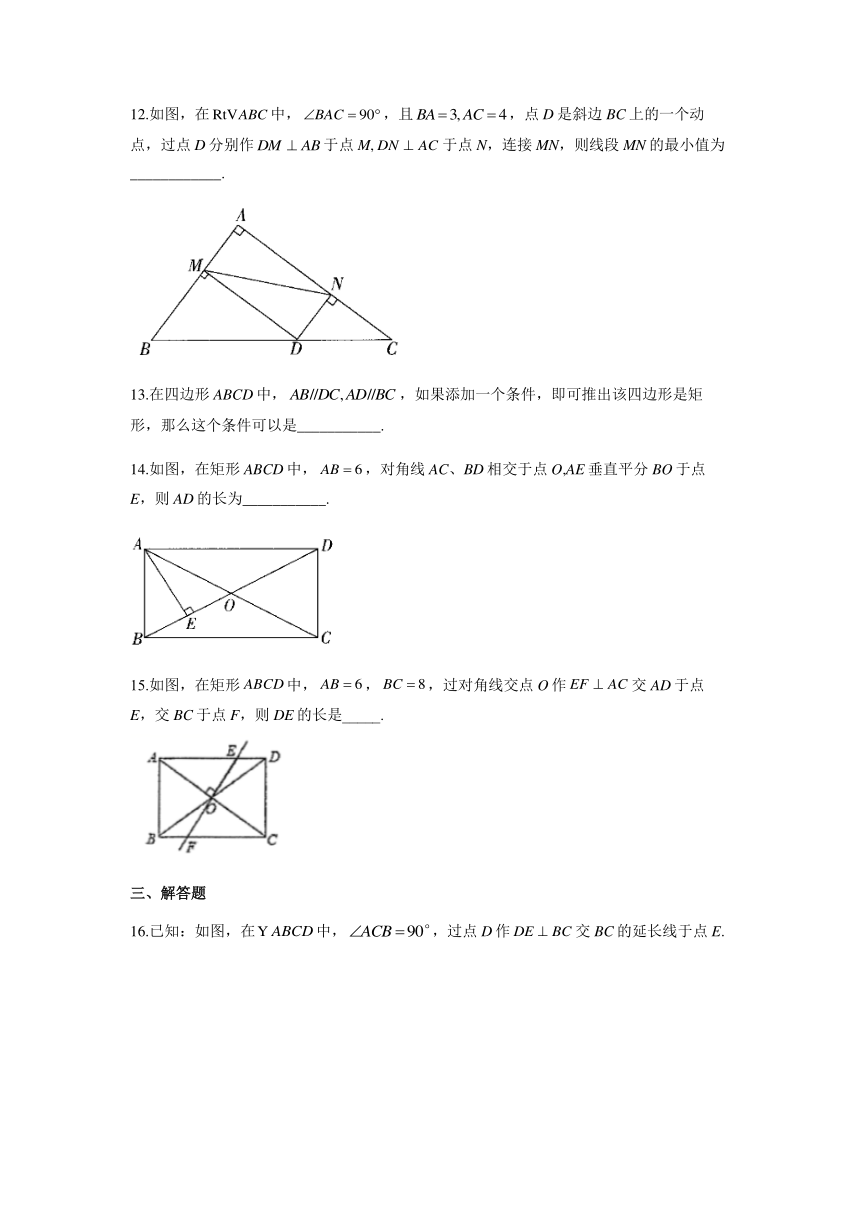
6.如图,在矩形纸片中,已知,折叠纸片,使边与对角线重合,点落在点处,折痕为,,则的长为( )
A.3 B.4 C.5 D.6
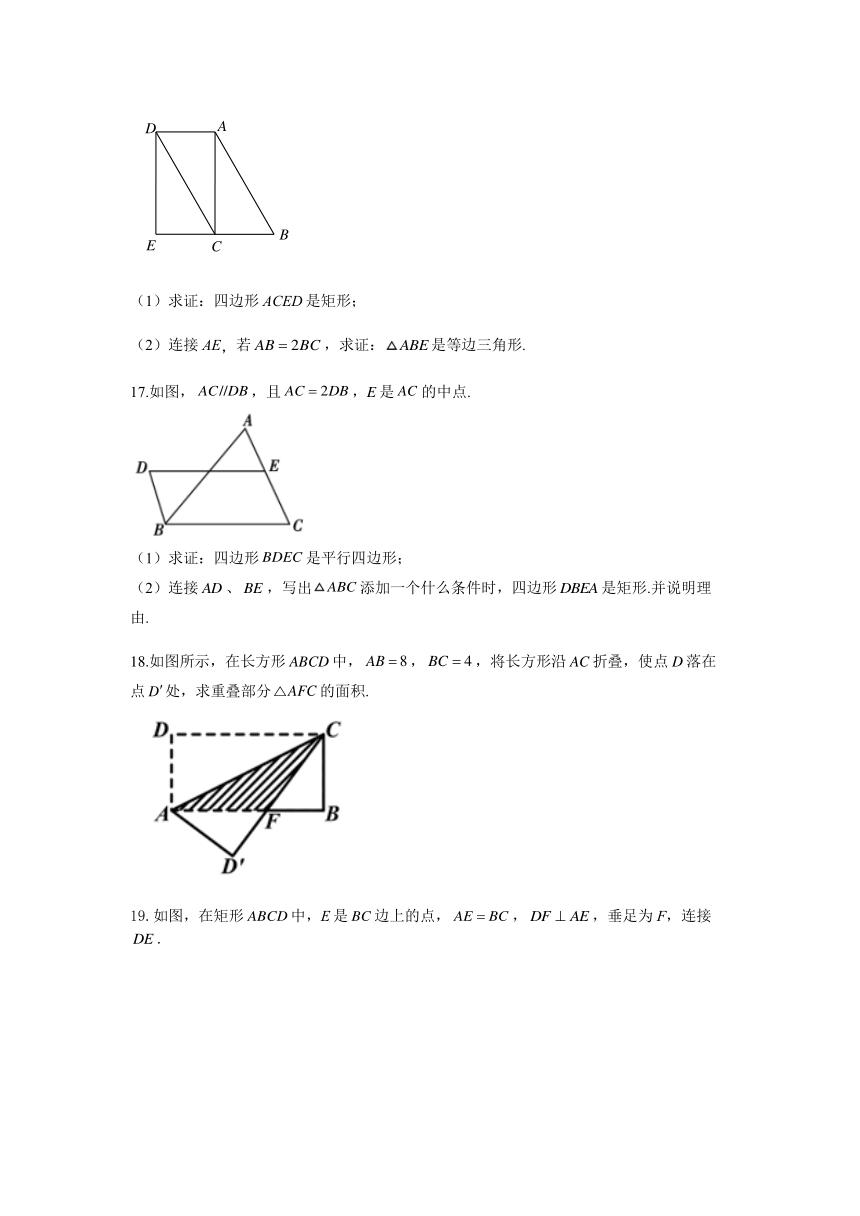
7.如图,把一块含有30°角的直角三角板ABC的直角顶点放在矩形桌面的一个顶点C处,桌面的另一个顶点F与三角板斜边相交于点F,AC与EF交于点G,如果,那么的 度数为( )
A.10° B.20° C.30° D.40°
8.如图,四边形是矩形,点E和点F是矩形外两点,于点,则长是( )
A. B. C. D.
9.如图,延长矩形ABCD的边BC至点E,使,连接AE,如果,那么( )
A.18° B.19° C.20° D.40°
10.已知一矩形的两邻边长分别为10cm和15cm,其中一个内角的平分线分长边为两部分,则这两部分的长分别为( )
A.6cm和9cm B.5cm和10cm C.4cm和l1cm D.7cm和8cm
二、填空题
11.如图,矩形ABCD中,E在AD上,且,矩形的周长为16,则AE的长是_____________.
12.如图,在中,,且,点D是斜边BC上的一个动点,过点D分别作于点M,于点N,连接MN,则线段MN的最小值为____________.
13.在四边形ABCD中,,如果添加一个条件,即可推出该四边形是矩形,那么这个条件可以是___________.
14.如图,在矩形ABCD中,,对角线AC、BD相交于点O,AE垂直平分BO于点E,则AD的长为___________.
15.如图,在矩形中,,,过对角线交点O作交AD于点E,交BC于点F,则DE的长是_____.
三、解答题
16.已知:如图,在中,,过点D作交BC的延长线于点E.
(1)求证:四边形ACED是矩形;
(2)连接AE,若,求证:是等边三角形.
17.如图,,且,E是的中点.
(1)求证:四边形是平行四边形;
(2)连接、,写出添加一个什么条件时,四边形是矩形.并说明理由.
18.如图所示,在长方形ABCD中,,,将长方形沿AC折叠,使点D落在点处,求重叠部分的面积.
19.如图,在矩形中,E是边上的点,,,垂足为F,连接.
(1)求证:;
(2)若,求矩形的面积.
20.如图点E,F分别是矩形ABCD的边AD,AB上一点,若,且
(1)求证:点F为AB的中点.
(2)延长EF与CB的延长线相交于点H,连接AH,已知,求AH的值.
参考答案
1.答案:B
解析:矩形的对角线互相平分且相等,但不一定互相垂直,故选项A错误,B正确;对角线相等的四边形不一定为矩形,故选项C错误;对角线互相平分的四边形为平行四边形,不一定为矩形,故选项D错误.
2.答案:C
解析:四边形ABCD的对角线相交于点O,且互相平分,四边形ABCD是平行四边形,
若,则四边形ABCD是矩形,
故选项A不符合题意;
若,则四边形ABCD是矩形,故选项B不符合题意;
若,则四边形ABCD是菱形,故选项C符合题意;
四边形ABCD是平行四边形,
。
若,则,则四边形ABCD是矩形,故选项D不符合题意.故选C.
3.答案:B
解析:A.邻边相等的平行四边形不一定是矩形,故A错误;B.对角线相等的平行四边形是矩形,故B正确;C.对角线互相垂直的平行四边形不一定是矩形,故C错误;D.对角线平分每一组对角的平行四边形不一定是矩形,故D错误.故选B.
4.答案:D
解析:四边形ABCD是矩形,,
为等边三角形,
.故选D.
5.答案:D
6.答案:D
解析:由折叠可知,,,
根据矩形的性质得,,所以.
因为,所以.
在中,根据勾股定理得,
在中,设,则,
由勾股定理得,
解得.
7.答案:B
解析:四边形CDEF为矩形,,.为的外角,且,.故选B.
8.答案:C
9.答案:B
解析:,,.故选B.
10.答案:B
解析:如图,在矩形ABCD中,BE是角平分线,
.
,
,
,
.
点E分长边为两部分,
,
,
,
则0.故选B.
11.答案:3
解析:设,四边形ABCD是矩形,
,
,
,
,
,
在和中,,
,
,
,
矩形ABCD的周长为16,
,解得,即.
12.答案:
解析:,且,
,
,
,
四边形DMAN是矩形,连接AD,则,
当时,AD的值最小,
此时的面积,
,
MN的最小值为.
13.答案:或或或(填一个即可)
解析:四边形ABCD是平行四边形,根据定义若加条件,需要加一个直角,即或或或,则可由定义:有一个角是直角的平行四边形是矩形,推出四边形ABCD是矩形.
14.答案:
解析:四边形ABCD是矩形,
.
AE垂直平分OB,
,
,
,
.
15.答案:.
16.答案:(1)证明:中,
,,,
,
,
,
四边形ACED是距形.
(2)证明:四边形ACED是距形
,
,
是等边三角形.
解析:
17.答案:(1)证明:∵E是中点,
∴.
∵,
∴.
又∵,
∴四边形是平行四边形.
(2)解:添加,理由如下:
连接、,如图,
∵,,
∴四边形是平行四边形.
∵,,
∴.
∴四边形是矩形.
解析:
18.答案:面积为10.
解析:在长方形ABCD中,
,.
又由折叠的性质可得,
,.
设,则.
在中, ,,,,
.解得.
.
19.答案:(1)见解析;(2)60
解析:(1)∵四边形为矩形,
(2)
,
得
20.答案:(1)证明见解析;(2)
解析:(1)证明:∵,
,
,
四边形是矩形,
,
,
,
,
,
,
,
,
为的中点;
(2)由(1)知,且,
,
,
,
,且,
,
,
∴,
∴,
故答案为:.
18.2.1矩形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列关于矩形的说法中正确的是( )
A.矩形的对角线互相垂直且平分 B.矩形的对角线相等且互相平分
C.对角线相等的四边形是矩形 D.对角线互相平分的四边形是矩形
2.如图,四边形ABCD的对角线相交于点O,且互相平分,若添加下列条件中的一个,不能判定四边形ABCD为矩形的是( )
A. B. C. D.
3.已知平行四边形ABCD中,下列条件:
①;
②;
③;
④AC平分,
其中能说明平行四边形ABCD是矩形的是( )
A.① B.② C.③ D.④
4.如图,矩形ABCD中,,则BD的长是( )
A.3 B.5 C. D.6
5.如图,在矩形中,与交于点O,若,则等于( )
A.90° B.100° C.110° D.120°
6.如图,在矩形纸片中,已知,折叠纸片,使边与对角线重合,点落在点处,折痕为,,则的长为( )
A.3 B.4 C.5 D.6
7.如图,把一块含有30°角的直角三角板ABC的直角顶点放在矩形桌面的一个顶点C处,桌面的另一个顶点F与三角板斜边相交于点F,AC与EF交于点G,如果,那么的 度数为( )
A.10° B.20° C.30° D.40°
8.如图,四边形是矩形,点E和点F是矩形外两点,于点,则长是( )
A. B. C. D.
9.如图,延长矩形ABCD的边BC至点E,使,连接AE,如果,那么( )
A.18° B.19° C.20° D.40°
10.已知一矩形的两邻边长分别为10cm和15cm,其中一个内角的平分线分长边为两部分,则这两部分的长分别为( )
A.6cm和9cm B.5cm和10cm C.4cm和l1cm D.7cm和8cm
二、填空题
11.如图,矩形ABCD中,E在AD上,且,矩形的周长为16,则AE的长是_____________.
12.如图,在中,,且,点D是斜边BC上的一个动点,过点D分别作于点M,于点N,连接MN,则线段MN的最小值为____________.
13.在四边形ABCD中,,如果添加一个条件,即可推出该四边形是矩形,那么这个条件可以是___________.
14.如图,在矩形ABCD中,,对角线AC、BD相交于点O,AE垂直平分BO于点E,则AD的长为___________.
15.如图,在矩形中,,,过对角线交点O作交AD于点E,交BC于点F,则DE的长是_____.
三、解答题
16.已知:如图,在中,,过点D作交BC的延长线于点E.
(1)求证:四边形ACED是矩形;
(2)连接AE,若,求证:是等边三角形.
17.如图,,且,E是的中点.
(1)求证:四边形是平行四边形;
(2)连接、,写出添加一个什么条件时,四边形是矩形.并说明理由.
18.如图所示,在长方形ABCD中,,,将长方形沿AC折叠,使点D落在点处,求重叠部分的面积.
19.如图,在矩形中,E是边上的点,,,垂足为F,连接.
(1)求证:;
(2)若,求矩形的面积.
20.如图点E,F分别是矩形ABCD的边AD,AB上一点,若,且
(1)求证:点F为AB的中点.
(2)延长EF与CB的延长线相交于点H,连接AH,已知,求AH的值.
参考答案
1.答案:B
解析:矩形的对角线互相平分且相等,但不一定互相垂直,故选项A错误,B正确;对角线相等的四边形不一定为矩形,故选项C错误;对角线互相平分的四边形为平行四边形,不一定为矩形,故选项D错误.
2.答案:C
解析:四边形ABCD的对角线相交于点O,且互相平分,四边形ABCD是平行四边形,
若,则四边形ABCD是矩形,
故选项A不符合题意;
若,则四边形ABCD是矩形,故选项B不符合题意;
若,则四边形ABCD是菱形,故选项C符合题意;
四边形ABCD是平行四边形,
。
若,则,则四边形ABCD是矩形,故选项D不符合题意.故选C.
3.答案:B
解析:A.邻边相等的平行四边形不一定是矩形,故A错误;B.对角线相等的平行四边形是矩形,故B正确;C.对角线互相垂直的平行四边形不一定是矩形,故C错误;D.对角线平分每一组对角的平行四边形不一定是矩形,故D错误.故选B.
4.答案:D
解析:四边形ABCD是矩形,,
为等边三角形,
.故选D.
5.答案:D
6.答案:D
解析:由折叠可知,,,
根据矩形的性质得,,所以.
因为,所以.
在中,根据勾股定理得,
在中,设,则,
由勾股定理得,
解得.
7.答案:B
解析:四边形CDEF为矩形,,.为的外角,且,.故选B.
8.答案:C
9.答案:B
解析:,,.故选B.
10.答案:B
解析:如图,在矩形ABCD中,BE是角平分线,
.
,
,
,
.
点E分长边为两部分,
,
,
,
则0.故选B.
11.答案:3
解析:设,四边形ABCD是矩形,
,
,
,
,
,
在和中,,
,
,
,
矩形ABCD的周长为16,
,解得,即.
12.答案:
解析:,且,
,
,
,
四边形DMAN是矩形,连接AD,则,
当时,AD的值最小,
此时的面积,
,
MN的最小值为.
13.答案:或或或(填一个即可)
解析:四边形ABCD是平行四边形,根据定义若加条件,需要加一个直角,即或或或,则可由定义:有一个角是直角的平行四边形是矩形,推出四边形ABCD是矩形.
14.答案:
解析:四边形ABCD是矩形,
.
AE垂直平分OB,
,
,
,
.
15.答案:.
16.答案:(1)证明:中,
,,,
,
,
,
四边形ACED是距形.
(2)证明:四边形ACED是距形
,
,
是等边三角形.
解析:
17.答案:(1)证明:∵E是中点,
∴.
∵,
∴.
又∵,
∴四边形是平行四边形.
(2)解:添加,理由如下:
连接、,如图,
∵,,
∴四边形是平行四边形.
∵,,
∴.
∴四边形是矩形.
解析:
18.答案:面积为10.
解析:在长方形ABCD中,
,.
又由折叠的性质可得,
,.
设,则.
在中, ,,,,
.解得.
.
19.答案:(1)见解析;(2)60
解析:(1)∵四边形为矩形,
(2)
,
得
20.答案:(1)证明见解析;(2)
解析:(1)证明:∵,
,
,
四边形是矩形,
,
,
,
,
,
,
,
,
为的中点;
(2)由(1)知,且,
,
,
,
,且,
,
,
∴,
∴,
故答案为:.
