8.1认识不等式 课件(共10张PPT)
文档属性
| 名称 | 8.1认识不等式 课件(共10张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 00:00:00 | ||
图片预览




文档简介
(共10张PPT)
8.1 认识不等式
1
新课讲授
1元
问题 1
世纪公园的票价是:每人 5 元;一次购票满 30 张,每张票可少收 1 元. 某班有 27 名少先队员去世纪公园进行活动. 当领队王小华准备好了零钱到售票处买 27 张票时,爱动脑筋的李敏同学喊住了王小华,提议买 30 张票.但有的同学不明白,明明我们只有 27 个人,买 30 张票,岂不是“浪费”吗?
那么,究竟李敏的提议对不对呢?
是不是真的“浪费”呢?
思考
(1)27人每人付5元门票钱合算,还是按30人(多算3人)每人付4元合算呢
解:买 27 张票,要付款:5×27 = 135(元)
买 30 张票,要付款:4×30 = 120(元)
因为120<135
所以买 30 张票比买 27张票便宜。
表面上看是“浪费”
了 3 张票,实际上
反而节省了
(2) 设有x人要去世纪公园.
①如果x≥30,则按实际人数买票,则每张票只付______元;
②如果x<30,那么按实际人数买票x张,则要付款______元;
买30张票,要付款______。如果买30张票合算,则______<______
5x
4
120
120
5x
x 取哪些数值时,上式成立?
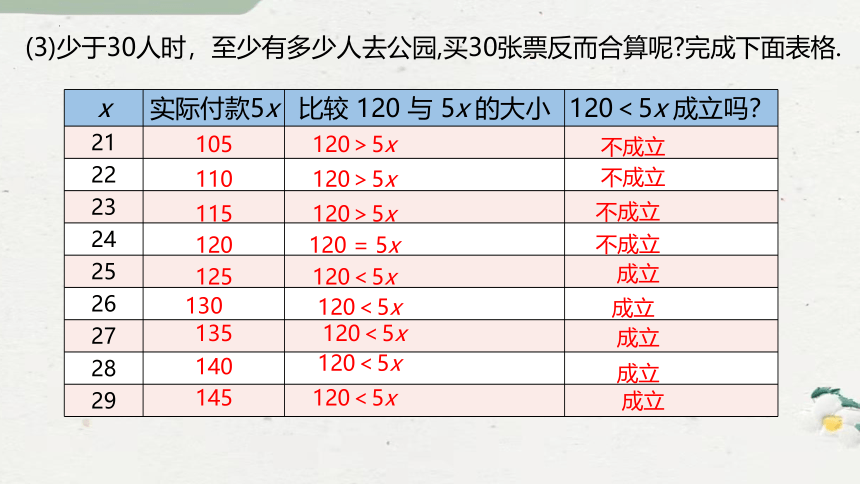
(3)少于30人时,至少有多少人去公园,买30张票反而合算呢 完成下面表格.
x 实际付款5x 比较 120 与 5x 的大小 120<5x 成立吗?
21
22
23
24
25
26
27
28
29
105
120>5x
不成立
110
120>5x
不成立
115
120>5x
不成立
120
120 = 5x
不成立
125
120<5x
成立
130
120<5x
成立
135
120<5x
成立
140
120<5x
成立
145
120<5x
成立
由上表可知,当 x =_________________________时, 120<5x 成立. 也就是说,少于 30 人时,至少要有_______人进公园,买 30 张票反而
合算.
25、26、27、28、29
25
1.不等式的定义:用不等号表示______________关系的式子,叫做不等式.表示不等关系的符号有>、 <、 ≥、≤、≠.
2.不等式的解: _____________________________叫做不等式的解.
如上例中,x=___________________________都是不等式120<5x的解。
概括
不等关系
使不等式成立的未知数的值
25、26、27、28、29
注意:实际问题不等式的解不仅要满足不等式,还要符合实际意义。
例 用不等式表示下列关系,
并分别写出两个满足不等式的数:
(1)x 的一半小于 – 1;
(2)y 与 4 的和大于 0.5;
(3)a 是负数;
(4)b 是非负数.
2
典例分析
分析:小于要用“____”号,大于要用“____”号,负数比0____
非负数指的是____________。
>
<
小
正数和0
解:(1) 如 x = – 3,– 4.
(2)y + 4>0.5. 如 y = 0,1.
(3)a < 0.如 a = – 3,– 4.
(4)b 是非负数,即 b 不是负数,
所以b > 0 或 b = 0. 如 b = 0, 2.
b > 0 或 b = 0,通常可以表示成 b ≥ 0.
3
课堂练习
1.下列式子:① 3x = 5;② a>2;③ 3m – 1 ≤ 4;④ 5x + 6y;⑤ – 1>2中. 不等式有( )个.
A.2 B.3 C.4 D.5
B
2.下列各数中,哪些是不等式3x-1<2的解 哪些不是
-2, -1, -0.5, 0, 0.4, 1, 1.5, 2, 3 .
-2, -1, -0.5, 0, 0.4
思考:不等式的解有什么特别之处
(一元一次方程若有解,则只有一个解,而一个不等式若有解,一般有多个解或无数解)
5
课堂小结
1.不等式的定义:用不等号表示______________关系的式子,叫做不等式.表示不等关系的符号有>、 <、 ≥、≤、≠.
2.不等式的解: _____________________________叫做不等式的解.
不等关系
使不等式成立的未知数的值
3.一元一次方程若有解,则只有一个解;
而一个不等式若有解,一般有多个解或无数解.
8.1 认识不等式
1
新课讲授
1元
问题 1
世纪公园的票价是:每人 5 元;一次购票满 30 张,每张票可少收 1 元. 某班有 27 名少先队员去世纪公园进行活动. 当领队王小华准备好了零钱到售票处买 27 张票时,爱动脑筋的李敏同学喊住了王小华,提议买 30 张票.但有的同学不明白,明明我们只有 27 个人,买 30 张票,岂不是“浪费”吗?
那么,究竟李敏的提议对不对呢?
是不是真的“浪费”呢?
思考
(1)27人每人付5元门票钱合算,还是按30人(多算3人)每人付4元合算呢
解:买 27 张票,要付款:5×27 = 135(元)
买 30 张票,要付款:4×30 = 120(元)
因为120<135
所以买 30 张票比买 27张票便宜。
表面上看是“浪费”
了 3 张票,实际上
反而节省了
(2) 设有x人要去世纪公园.
①如果x≥30,则按实际人数买票,则每张票只付______元;
②如果x<30,那么按实际人数买票x张,则要付款______元;
买30张票,要付款______。如果买30张票合算,则______<______
5x
4
120
120
5x
x 取哪些数值时,上式成立?
(3)少于30人时,至少有多少人去公园,买30张票反而合算呢 完成下面表格.
x 实际付款5x 比较 120 与 5x 的大小 120<5x 成立吗?
21
22
23
24
25
26
27
28
29
105
120>5x
不成立
110
120>5x
不成立
115
120>5x
不成立
120
120 = 5x
不成立
125
120<5x
成立
130
120<5x
成立
135
120<5x
成立
140
120<5x
成立
145
120<5x
成立
由上表可知,当 x =_________________________时, 120<5x 成立. 也就是说,少于 30 人时,至少要有_______人进公园,买 30 张票反而
合算.
25、26、27、28、29
25
1.不等式的定义:用不等号表示______________关系的式子,叫做不等式.表示不等关系的符号有>、 <、 ≥、≤、≠.
2.不等式的解: _____________________________叫做不等式的解.
如上例中,x=___________________________都是不等式120<5x的解。
概括
不等关系
使不等式成立的未知数的值
25、26、27、28、29
注意:实际问题不等式的解不仅要满足不等式,还要符合实际意义。
例 用不等式表示下列关系,
并分别写出两个满足不等式的数:
(1)x 的一半小于 – 1;
(2)y 与 4 的和大于 0.5;
(3)a 是负数;
(4)b 是非负数.
2
典例分析
分析:小于要用“____”号,大于要用“____”号,负数比0____
非负数指的是____________。
>
<
小
正数和0
解:(1) 如 x = – 3,– 4.
(2)y + 4>0.5. 如 y = 0,1.
(3)a < 0.如 a = – 3,– 4.
(4)b 是非负数,即 b 不是负数,
所以b > 0 或 b = 0. 如 b = 0, 2.
b > 0 或 b = 0,通常可以表示成 b ≥ 0.
3
课堂练习
1.下列式子:① 3x = 5;② a>2;③ 3m – 1 ≤ 4;④ 5x + 6y;⑤ – 1>2中. 不等式有( )个.
A.2 B.3 C.4 D.5
B
2.下列各数中,哪些是不等式3x-1<2的解 哪些不是
-2, -1, -0.5, 0, 0.4, 1, 1.5, 2, 3 .
-2, -1, -0.5, 0, 0.4
思考:不等式的解有什么特别之处
(一元一次方程若有解,则只有一个解,而一个不等式若有解,一般有多个解或无数解)
5
课堂小结
1.不等式的定义:用不等号表示______________关系的式子,叫做不等式.表示不等关系的符号有>、 <、 ≥、≤、≠.
2.不等式的解: _____________________________叫做不等式的解.
不等关系
使不等式成立的未知数的值
3.一元一次方程若有解,则只有一个解;
而一个不等式若有解,一般有多个解或无数解.
