2021-2022学年广东省佛山市顺德区九年级(下)开学数学试卷(Word版含解析)
文档属性
| 名称 | 2021-2022学年广东省佛山市顺德区九年级(下)开学数学试卷(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 858.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 21:50:08 | ||
图片预览




文档简介
2021-2022学年广东省佛山市顺德区九年级(下)开学数学试卷
一、选择题(12个题,每题3分,共36分)
1.下列关系式能表示y关于x的反比例函数的是( )
A. B. C.y=2022x+1 D.y=2022x2+1
2.如图是由两个大小不一样的圆柱组成的几何体,几何体的左视图是( )
A. B. C. D.
3.在四边形ABCD中,∠A=∠B=∠C=90°.如果再添加一个条件可推出四边形是正方形,那么这个条件可以是( )
A.AB=CD B.BC=CD C.∠D=90° D.AC=BD
4.方程x2﹣6x+4=0的根是( )
A. B. C. D.
5.直角三角形两条直角边长分别是6和8,则斜边上的中线长为( )
A.3 B.4 C.5 D.6
6.如图,在平行四边形ABCD中,DE:EC=4:1,连接AE交BD于点F,则S△DEF:S△BAF为( )
A.3:4 B.9:16 C.16:25 D.4:1
7.若关于x的方程x2﹣5x+k=0有两个不相等的实数根,则k的取值范围是( )
A. B. C. D.
8.某班学生做“用频率估计概率”的实验时,某一结果出现如图所示的统计图,符合这一结果的实验可能是( )
A.从标有1,2,3,4,5,6的卡片中任抽一张是偶数
B.同时抛掷两枚相同硬币出现的结果是一正一反
C.从一副去掉大小王的扑克中任抽一张牌的花色是红桃
D.掷一个质地均匀的正六面体骰子得到向上的面点数小于3
9.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件不能满足△ADE∽△ACB的条件是( )
A.∠AED=∠B B.
C.AD BC=DE AC D.∠ADE=∠C
10.探索一元二次方程ax2+bx+c=0(a≠0)的一个正数解的过程如表:可以看出方程的一个正数解的取值范围为( )
x ﹣1 0 1 2 3 4
ax2+bx+c ﹣7 ﹣5 ﹣1 5 13 23
A.﹣1<x<0 B.0<x<1 C.1<x<2 D.﹣1<x<5
11.若A(﹣2,a),B(1,b),c(2,c)为反比例函数(k为常数)的图象上的三点,则a,b,c的大小关系是( )
A.a<b<c B.c<b<a C.a<c<b D.b<c<a
12.如图,∠ABD=∠CBE=90°,AB=BD,∠CAB=∠E.若BE=10,AD=4,则的值为( )
A. B. C. D.
二、填空题(5个题,每题4分,共20分)
13.四边形ABCD∽四边形A'B'C'D'.若∠D=90°,∠B'=108°,∠C'=92°,则∠A= °.
14.在Rt△ABC中,∠C=90°,BC=2,sinA=,则边AB的长为 .
15.在一个不透明的布袋里装有1个红球和2个白球,它们除颜色外其余都相同,若先摸出1个球,记下颜色后不放回,再摸出1个球,则两次摸出的球恰好一红一白的概率是 .
16.某商场出售一批商品,在销售中发现日销售量y(件)与销售价x(元)的变化关系如下表,写出y与x之间的函数关系式 .
售价x(元) 200 240 250 400
日销售量y(件) 30 25 24 15
17.如图,在Rt△ABC中,∠ACB=90°,AC=6,tanA=,将△ABC绕点C顺时针旋转得到△A'B'C,点A的对应点为A',若P为A'B'的中点,连接BP,则线段BP长度的最大值为 .
三、解答题(6个题,共64分)
18.某校园有旗杆AB在阳光下某一时刻的影子长为AG.高1.6米的标杆EF在同一时刻的影子为EM(其中AB,EF都与地面垂直).通过测量获得数据AG=7.5,EM=1米.
(1)在图中画出旗杆的影子;
(2)求旗杆AB的高度.
19.如图,一次函数y=ax+b与反比例函数y=(k≠0)的图象相交于点A(1,﹣3)和B(m,﹣1),连接OA、OB.
(1)求一次函数的解析式;
(2)求△OAB的面积.
20.如图,在菱形ABCD中,两条对角线相交于点O,F是边CD的中点,连接OF并延长到E,使FE=OF,连接CE,DE.
(1)求证:四边形OCED是矩形;
(2)若∠DAB=60°,菱形ABCD的面积为,求矩形OCED的周长.
21.某商品的进价是每件40元,当售价每件60元时,当天可售出300件.进行不同程度的涨价后,发现每涨价1元,当天销售量减少10件.设商品售价每件涨价x元(x为正整数)时,当天售出商品的利润为y元.
(1)求y与x之间的函数关系式;
(2)如何定价,才能使商品当天的销售利润达到6250元?
22.如图,在△ABC中,cos∠BAC=,AB=26,AC=15,BD⊥AC,垂足为D,E是BD的中点,AE与BC交于点F.
(1)求∠CBD的正切值;
(2)求的值.
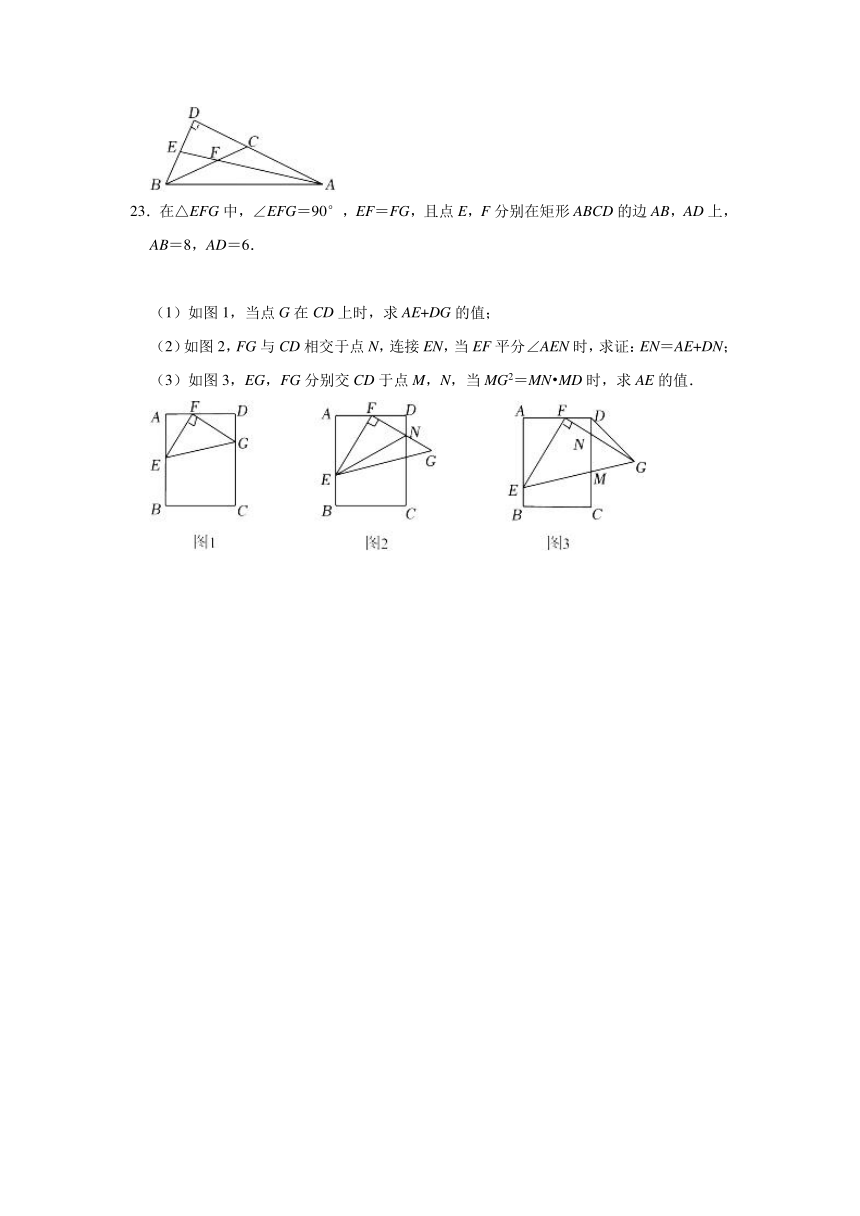
23.在△EFG中,∠EFG=90°,EF=FG,且点E,F分别在矩形ABCD的边AB,AD上,AB=8,AD=6.
(1)如图1,当点G在CD上时,求AE+DG的值;
(2)如图2,FG与CD相交于点N,连接EN,当EF平分∠AEN时,求证:EN=AE+DN;
(3)如图3,EG,FG分别交CD于点M,N,当MG2=MN MD时,求AE的值.
参考答案
一、选择题(12个题,每题3分,共36分)
1.下列关系式能表示y关于x的反比例函数的是( )
A. B. C.y=2022x+1 D.y=2022x2+1
【分析】根据反比例函数的定义直接解答即可.
解:A、y2是x的正比例函数,故本选项不合题意;
B、y是x的反比例函数,故本选项符合题意;
C、y是x的一次函数,故本选项不合题意;
D、y是x的二次函数,故本选项不合题意.
故选:B.
2.如图是由两个大小不一样的圆柱组成的几何体,几何体的左视图是( )
A. B. C. D.
【分析】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.
解:从左面看,底层是较大的矩形,上层中间是一个较小的矩形.
故选:A.
3.在四边形ABCD中,∠A=∠B=∠C=90°.如果再添加一个条件可推出四边形是正方形,那么这个条件可以是( )
A.AB=CD B.BC=CD C.∠D=90° D.AC=BD
【分析】先判断四边形ABCD是矩形,由正方形的判定可直接判断B正确.
解:∵四边形ABCD中,∠A=∠B=∠C=90°,
∴四边形ABCD是矩形,
∴AD=CD,∠D=90°,AC=BD,
故A,C,D不符合题意,
当AB=AD时,即一组邻边相等时,矩形ABCD为正方形,
故C符合题意,
故选:B.
4.方程x2﹣6x+4=0的根是( )
A. B. C. D.
【分析】将常数项移到方程的右边,两边都加上一次项系数一半的平方配成完全平方式后,再开方即可得.
解:∵x2﹣6x+4=0,
∴x2﹣6x=﹣4,
∴x2﹣6x+9=﹣4+9,即(x﹣3)2=5,
∴x﹣3=±,
∴x1=3+,x2=3﹣.
故选:C.
5.直角三角形两条直角边长分别是6和8,则斜边上的中线长为( )
A.3 B.4 C.5 D.6
【分析】利用勾股定理求出斜边,再根据直角三角形斜边上的中线等于斜边的一半解答.
解:∵直角三角形两条直角边长分别是6和8,
∴斜边==10,
∴斜边上的中线长=×10=5.
故选:C.
6.如图,在平行四边形ABCD中,DE:EC=4:1,连接AE交BD于点F,则S△DEF:S△BAF为( )
A.3:4 B.9:16 C.16:25 D.4:1
【分析】根据相似三角形的面积比等于相似比的平方即可求解.
解:∵DE:EC=4:1,
∴DE:CD=4:5,
∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,
∴△DEF∽△BAF,
∴,
故选:C.
7.若关于x的方程x2﹣5x+k=0有两个不相等的实数根,则k的取值范围是( )
A. B. C. D.
【分析】利用根的判别式的意义得到Δ=(﹣5)2﹣4k>0,然后解不等式即可.
解:根据题意得Δ=(﹣5)2﹣4k>0,
解得k<.
故选:A.
8.某班学生做“用频率估计概率”的实验时,某一结果出现如图所示的统计图,符合这一结果的实验可能是( )
A.从标有1,2,3,4,5,6的卡片中任抽一张是偶数
B.同时抛掷两枚相同硬币出现的结果是一正一反
C.从一副去掉大小王的扑克中任抽一张牌的花色是红桃
D.掷一个质地均匀的正六面体骰子得到向上的面点数小于3
【分析】根据频率估计概率分别对每一项进行分析,即可得出答案.
解:A、从标有1,2,3,4,5,6的六张卡片中任抽一张,出现偶数的概率是=,不符合这一结果,故此选项不符合题意;
B、同时抛掷两枚相同硬币出现的结果是一正一反的概率是,不符合这一结果,故此选项符合题意;
C、一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率是=0.25,不符合这一结果,故此选项不符合题意;
D、掷一个质地均匀的正六面体骰子得到向上的面点数小于3:=,符合这一结果,故此选项符合题意;
故选:D.
9.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件不能满足△ADE∽△ACB的条件是( )
A.∠AED=∠B B.
C.AD BC=DE AC D.∠ADE=∠C
【分析】根据相似三角形的判定逐一判断即可.
解:∵∠AED=∠B,∠A=∠A,
∴△ADE∽△ACB,
故A正确,不符合题意;
∵,∠A=∠A,
∴△ADE∽△ACB,
故B正确,不符合题意;
∵AD BC=DE AC,
∴,无法判断△ADE∽△ACB,
故C符合题意,
∵∠ADE=∠C,∠A=∠A,
∴△ADE∽△ABC,
故D正确,不符合题意;
故选:C.
10.探索一元二次方程ax2+bx+c=0(a≠0)的一个正数解的过程如表:可以看出方程的一个正数解的取值范围为( )
x ﹣1 0 1 2 3 4
ax2+bx+c ﹣7 ﹣5 ﹣1 5 13 23
A.﹣1<x<0 B.0<x<1 C.1<x<2 D.﹣1<x<5
【分析】根据表格中的数据,可以发现当x=1时,ax2+bx+c=﹣1<0,当x=2时,ax2+bx+c=5>0,从而可以得到整数a、b的值.
解:由表格可得,
当x=1时,ax2+bx+c=﹣1<0,当x=2时,ax2+bx+c=5>0,
∴x2+3x﹣5=0的一个正数解为1和2之间,
即方程的一个正数解的取值范围为1<x<2,
故选:C.
11.若A(﹣2,a),B(1,b),c(2,c)为反比例函数(k为常数)的图象上的三点,则a,b,c的大小关系是( )
A.a<b<c B.c<b<a C.a<c<b D.b<c<a
【分析】根据k的值确定双曲线所在的象限,进而明确函数的增减性,再根据点A(﹣1,a),B(1,b),C(2,c)所在的象限,确定a、b、c大小关系.
解:∵k为常数,
∴k2+1>0,
∴反比例函数(k为常数)的图象位于一三象限,且在每个象限内,y随x的增大而减小,
因此点A(﹣2,a)在第三象限,而B(1,b),C(2,c)在第一象限,
∴a<0,b>c>0,
∴a<c<b,
故选:C.
12.如图,∠ABD=∠CBE=90°,AB=BD,∠CAB=∠E.若BE=10,AD=4,则的值为( )
A. B. C. D.
【分析】先由AB=BD,∠ABD=90°,根据勾股定理求出AB的长为4,再证明△ABC∽△EBD,则===,得出问题的答案.
解:如图,∵AB=BD,∠ABD=90°,
∴AD2=AB2+BD2=2AB2,
∵AD=4,
∴(4)2=2AB2,
∴AB=4,
∵∠CBE=90°,
∴∠ABC=∠DBE=90°﹣∠CBD,
∵∠CAB=∠E,
∴△ABC∽△EBD,
∵BE=10,
∴===,
∴的值为,
故选:D.
二、填空题(5个题,每题4分,共20分)
13.四边形ABCD∽四边形A'B'C'D'.若∠D=90°,∠B'=108°,∠C'=92°,则∠A= 70 °.
【分析】根据相似多边形的对应角相等可得.
解:四边形ABCD∽四边形A′B′C′D′,
则∠B=∠B′=108°,∠C=∠C′=92′
四边形ABCD的内角和是360°,
因而∠A=360°﹣90°﹣108°﹣92°=70°.
故答案为:70.
14.在Rt△ABC中,∠C=90°,BC=2,sinA=,则边AB的长为 8 .
【分析】在直角三角形中,利用∠A的正弦、BC与AB间关系,计算得结论.
解:Rt△ABC中,
∵sinA==,BC=2,
∴AB=2×4=8.
故答案为:8.
15.在一个不透明的布袋里装有1个红球和2个白球,它们除颜色外其余都相同,若先摸出1个球,记下颜色后不放回,再摸出1个球,则两次摸出的球恰好一红一白的概率是 .
【分析】画树状图,共有6种等可能的结果,其中两次摸出的球恰好一红一白的结果有4种,再由概率公式求解即可.
解:画树状图如下:
共有6种等可能的结果,其中两次摸出的球恰好一红一白的结果有4种,
∴两次摸出的球恰好一红一白的概率为=,
故答案为:.
16.某商场出售一批商品,在销售中发现日销售量y(件)与销售价x(元)的变化关系如下表,写出y与x之间的函数关系式 .
售价x(元) 200 240 250 400
日销售量y(件) 30 25 24 15
【分析】根据表格数据可得日销售量y(件)与销售价x(元)的乘积总为6000,则可求得此题结果.
解:由题意得,日销售量y(件)与销售价x(元)的乘积总为6000,
即xy=6000,
变形得,y=,
故答案为:y=.
17.如图,在Rt△ABC中,∠ACB=90°,AC=6,tanA=,将△ABC绕点C顺时针旋转得到△A'B'C,点A的对应点为A',若P为A'B'的中点,连接BP,则线段BP长度的最大值为 4+ .
【分析】连接CP,由勾股定理求出AB=2,由旋转的性质得出A'B'=AB=2,∠A'CB'=∠ACB=90°,由直角三角形的性质求出CP=A'B'=,由题意得出点P在以C为圆心,4为半径的圆上运动,则可求出答案.
解:连接CP,
∵∠ACB=90°,AC=6,tanA=,
∴BC=4,
∴AB===2,
∵将△ABC绕点C旋转,得到△A'B'C,
∴A'B'=AB=2,∠A'CB'=∠ACB=90°,
∵P为A'B′的中点,
∴CP=A'B'=,
∴在旋转的过程中,点P在以C为圆心,4为半径的圆上运动,
∴当B,C,P三点共线时,BP有最大值,
∴BP的最大值为4+.
故答案为:4+.
三、解答题(6个题,共64分)
18.某校园有旗杆AB在阳光下某一时刻的影子长为AG.高1.6米的标杆EF在同一时刻的影子为EM(其中AB,EF都与地面垂直).通过测量获得数据AG=7.5,EM=1米.
(1)在图中画出旗杆的影子;
(2)求旗杆AB的高度.
【分析】(1)根点B作BG∥FM交ZM于点G,线段AG即为所求;
(2)利用相似三角形的性质求解即可.
解:(1)如图,线段AG即为所求;
(2)∵AB,EF在同一时刻的阳光下,
∴BG∥FM,故∠BGA=∠FME.
∵∠BAG=∠FEM=90°,
∴△BAG∽△FEM,
∴=,即=,
∴AB=12(米).
答:旗杆AB的高度为12米.
19.如图,一次函数y=ax+b与反比例函数y=(k≠0)的图象相交于点A(1,﹣3)和B(m,﹣1),连接OA、OB.
(1)求一次函数的解析式;
(2)求△OAB的面积.
【分析】(1)把A点的坐标代入反例函数解析式即可求出反比例函数解析式,进而得出B的坐标,把A、B的坐标代入一次函数解析式即可求出一次函数解析式;
(2)△AOB的面积=△BOD的面积﹣△AOD的面积.
解:(1)∵反比例函数y=(k≠0)的图象经过A(1,﹣3),
∴﹣3=.
∴k=﹣3,
∴反比例函数的表达式为y=﹣.
∵B(m,﹣1)在y=﹣上,
∴m=3.
∴B点坐标为(3,﹣1);
把A,B两点的坐标代入y=ax+b,得,
解得:,
∴一次函数的表达式为:y=x﹣4;
(2)当x=0时,y=﹣4.
∴D点坐标为(0,﹣4).
∴S△AOB=S△BOD﹣S△AOD=﹣=4.
20.如图,在菱形ABCD中,两条对角线相交于点O,F是边CD的中点,连接OF并延长到E,使FE=OF,连接CE,DE.
(1)求证:四边形OCED是矩形;
(2)若∠DAB=60°,菱形ABCD的面积为,求矩形OCED的周长.
【分析】(1)由已知CF=DF,EF=OF,得到四边形OCED是平行四边形,由菱形的性质得到AC⊥BD,即可证得四边形OCED是矩形;
(2)由已知及菱形的性质证得△ABD是等边三角形,由含30度直角三角形的性质得到AD=2OD,设OD=k,则AD=2k,由勾股定理求得AO=k,由菱形的面积公式求出k,进而可求出矩形OCED的周长.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∵CF=DF,EF=OF,
∴四边形OCED是平行四边形,
∵∠DOC=90°,
∴四边形OCED是矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=AD,AC⊥BD,AO=CO,BO=DO,
∵∠DAB=60°,
∴△ABD是等边三角形,
∴AD=BD=AB,∠DAO=∠BAO=30°,
∴AD=2OD,
设OD=k,则AD=2k,
∴BD=2k,
在Rt△AOD中,
AO===k,AC=2k.
∵S菱形ABCD=AC BD,
∴×2k×2k=8,
∴k2=4,
∵k>0,
∴k=2,
∴CO=2,OD=2,
∴矩形OCED的周长=2(OD+OC)=2(2+2)=4+4.
21.某商品的进价是每件40元,当售价每件60元时,当天可售出300件.进行不同程度的涨价后,发现每涨价1元,当天销售量减少10件.设商品售价每件涨价x元(x为正整数)时,当天售出商品的利润为y元.
(1)求y与x之间的函数关系式;
(2)如何定价,才能使商品当天的销售利润达到6250元?
【分析】(1)根据总利润=每件利润×销售量,即可列出函数关系式;
(2)令y=6250,解关于x的方程即可得答案.
解:(1)根据题意得:y=(60+x﹣40)(300﹣10x)
=﹣10x2+100x+6000.
∴y与x之间的函数关系式为y=﹣10x2+100x+6000.
(2)令y=6250,则﹣10x2+100x+6000=6250,
解得x1=x2=5,
此时60+x=60+565(元),
∴当售价为65元时,当天的利润达到6250元.
22.如图,在△ABC中,cos∠BAC=,AB=26,AC=15,BD⊥AC,垂足为D,E是BD的中点,AE与BC交于点F.
(1)求∠CBD的正切值;
(2)求的值.
【分析】(1)由根据余弦的定义以及勾股定理分别求出AD与BD的长,再由AC=15求得CD的长即可求解;
(2)过E作EM∥DC交BC于M,由EM∥CA得△EMF∽△ACF,从而得出比例式求解即可.
解:(1)Rt△ADB中,AB=26,cos∠BAC=,
∴AD=24,
由勾股定理,得BD==10,
∵AC=15,
∴CD=9,
∴tan∠CBD==,
∴∠CBD的正切值为;
(2)过E作EM∥DC交BC于M,
∵E是BD的中点,
∴EM=DC=4.5,DE=5,
∵EM∥CA,
∴△EMF∽△ACF,
∴===,
∴=,
23.在△EFG中,∠EFG=90°,EF=FG,且点E,F分别在矩形ABCD的边AB,AD上,AB=8,AD=6.
(1)如图1,当点G在CD上时,求AE+DG的值;
(2)如图2,FG与CD相交于点N,连接EN,当EF平分∠AEN时,求证:EN=AE+DN;
(3)如图3,EG,FG分别交CD于点M,N,当MG2=MN MD时,求AE的值.
【分析】(1)利用矩形的性质证明△DFG≌△AEF(AAS),得AF=DG,AE=DF,可得答案;
(2)延长NF,EA相交于H,首先利用ASA证明△HFE≌△NFE,得FH=FN,HE=NE,再利用AAS证明△HFA≌△NFD,得AH=DN,可得结论;
(3)过点G作GP⊥AD交AD的延长线于P,利用△MGN∽△MDG,得∠GDM=45°,∠PDG=45°,再利用AAS证明△PFG≌△AEF,得AF=PG,AE=PF即可.
【解答】(1)解:∵四边形ABCD是矩形,
∴∠A=∠D=90°,EF=FG,
∵∠EFG=90°,
∴∠AFE+∠DFN=90°,∠AFE+∠AEF=90°,
∴∠DFN=∠AEF.
∴△DFG≌△AEF(AAS),
∴AF=DG,AE=DF,
∴AE+DG=AF+DF=AD=6;
(2)证明:如图,延长NF,EA相交于H,
∴∠HFE=90°,∠HAF=90°,
∵∠HFE=∠NFE,EF=EF,∠HEF=∠NEF,
∴△HFE≌△NFE(ASA),
∴FH=FN,HE=NE,
∵∠AFH=∠DFN,∠HAF=∠D,
∴△HFA≌△NFD(AAS),
∴AH=DN,
∵EH=AE+AH=AE+DN,
∴EN=AE+DN;
(3)解:如图,过点G作GP⊥AD交AD的延长线于P,
∴∠P=90°,
∵MG2=MN MD,
∴=,
∵∠GMN=∠DMG,
∴△MGN∽△MDG,
∴∠GDM=45°,∠PDG=45°,
∴△PDG是等腰直角三角形,PG=PD,
∵∠AFE+∠PFG=90°,∠AFE+∠AEF=90°,
∴∠PFG=∠AEF,
∵∠A=∠P=90°,EF=FG,
∴△PFG≌△AEF(AAS),
∴AF=PG,AE=PF,
∴AE=PD+DF=AF+DF=AD=6.
一、选择题(12个题,每题3分,共36分)
1.下列关系式能表示y关于x的反比例函数的是( )
A. B. C.y=2022x+1 D.y=2022x2+1
2.如图是由两个大小不一样的圆柱组成的几何体,几何体的左视图是( )
A. B. C. D.
3.在四边形ABCD中,∠A=∠B=∠C=90°.如果再添加一个条件可推出四边形是正方形,那么这个条件可以是( )
A.AB=CD B.BC=CD C.∠D=90° D.AC=BD
4.方程x2﹣6x+4=0的根是( )
A. B. C. D.
5.直角三角形两条直角边长分别是6和8,则斜边上的中线长为( )
A.3 B.4 C.5 D.6
6.如图,在平行四边形ABCD中,DE:EC=4:1,连接AE交BD于点F,则S△DEF:S△BAF为( )
A.3:4 B.9:16 C.16:25 D.4:1
7.若关于x的方程x2﹣5x+k=0有两个不相等的实数根,则k的取值范围是( )
A. B. C. D.
8.某班学生做“用频率估计概率”的实验时,某一结果出现如图所示的统计图,符合这一结果的实验可能是( )
A.从标有1,2,3,4,5,6的卡片中任抽一张是偶数
B.同时抛掷两枚相同硬币出现的结果是一正一反
C.从一副去掉大小王的扑克中任抽一张牌的花色是红桃
D.掷一个质地均匀的正六面体骰子得到向上的面点数小于3
9.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件不能满足△ADE∽△ACB的条件是( )
A.∠AED=∠B B.
C.AD BC=DE AC D.∠ADE=∠C
10.探索一元二次方程ax2+bx+c=0(a≠0)的一个正数解的过程如表:可以看出方程的一个正数解的取值范围为( )
x ﹣1 0 1 2 3 4
ax2+bx+c ﹣7 ﹣5 ﹣1 5 13 23
A.﹣1<x<0 B.0<x<1 C.1<x<2 D.﹣1<x<5
11.若A(﹣2,a),B(1,b),c(2,c)为反比例函数(k为常数)的图象上的三点,则a,b,c的大小关系是( )
A.a<b<c B.c<b<a C.a<c<b D.b<c<a
12.如图,∠ABD=∠CBE=90°,AB=BD,∠CAB=∠E.若BE=10,AD=4,则的值为( )
A. B. C. D.
二、填空题(5个题,每题4分,共20分)
13.四边形ABCD∽四边形A'B'C'D'.若∠D=90°,∠B'=108°,∠C'=92°,则∠A= °.
14.在Rt△ABC中,∠C=90°,BC=2,sinA=,则边AB的长为 .
15.在一个不透明的布袋里装有1个红球和2个白球,它们除颜色外其余都相同,若先摸出1个球,记下颜色后不放回,再摸出1个球,则两次摸出的球恰好一红一白的概率是 .
16.某商场出售一批商品,在销售中发现日销售量y(件)与销售价x(元)的变化关系如下表,写出y与x之间的函数关系式 .
售价x(元) 200 240 250 400
日销售量y(件) 30 25 24 15
17.如图,在Rt△ABC中,∠ACB=90°,AC=6,tanA=,将△ABC绕点C顺时针旋转得到△A'B'C,点A的对应点为A',若P为A'B'的中点,连接BP,则线段BP长度的最大值为 .
三、解答题(6个题,共64分)
18.某校园有旗杆AB在阳光下某一时刻的影子长为AG.高1.6米的标杆EF在同一时刻的影子为EM(其中AB,EF都与地面垂直).通过测量获得数据AG=7.5,EM=1米.
(1)在图中画出旗杆的影子;
(2)求旗杆AB的高度.
19.如图,一次函数y=ax+b与反比例函数y=(k≠0)的图象相交于点A(1,﹣3)和B(m,﹣1),连接OA、OB.
(1)求一次函数的解析式;
(2)求△OAB的面积.
20.如图,在菱形ABCD中,两条对角线相交于点O,F是边CD的中点,连接OF并延长到E,使FE=OF,连接CE,DE.
(1)求证:四边形OCED是矩形;
(2)若∠DAB=60°,菱形ABCD的面积为,求矩形OCED的周长.
21.某商品的进价是每件40元,当售价每件60元时,当天可售出300件.进行不同程度的涨价后,发现每涨价1元,当天销售量减少10件.设商品售价每件涨价x元(x为正整数)时,当天售出商品的利润为y元.
(1)求y与x之间的函数关系式;
(2)如何定价,才能使商品当天的销售利润达到6250元?
22.如图,在△ABC中,cos∠BAC=,AB=26,AC=15,BD⊥AC,垂足为D,E是BD的中点,AE与BC交于点F.
(1)求∠CBD的正切值;
(2)求的值.
23.在△EFG中,∠EFG=90°,EF=FG,且点E,F分别在矩形ABCD的边AB,AD上,AB=8,AD=6.
(1)如图1,当点G在CD上时,求AE+DG的值;
(2)如图2,FG与CD相交于点N,连接EN,当EF平分∠AEN时,求证:EN=AE+DN;
(3)如图3,EG,FG分别交CD于点M,N,当MG2=MN MD时,求AE的值.
参考答案
一、选择题(12个题,每题3分,共36分)
1.下列关系式能表示y关于x的反比例函数的是( )
A. B. C.y=2022x+1 D.y=2022x2+1
【分析】根据反比例函数的定义直接解答即可.
解:A、y2是x的正比例函数,故本选项不合题意;
B、y是x的反比例函数,故本选项符合题意;
C、y是x的一次函数,故本选项不合题意;
D、y是x的二次函数,故本选项不合题意.
故选:B.
2.如图是由两个大小不一样的圆柱组成的几何体,几何体的左视图是( )
A. B. C. D.
【分析】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.
解:从左面看,底层是较大的矩形,上层中间是一个较小的矩形.
故选:A.
3.在四边形ABCD中,∠A=∠B=∠C=90°.如果再添加一个条件可推出四边形是正方形,那么这个条件可以是( )
A.AB=CD B.BC=CD C.∠D=90° D.AC=BD
【分析】先判断四边形ABCD是矩形,由正方形的判定可直接判断B正确.
解:∵四边形ABCD中,∠A=∠B=∠C=90°,
∴四边形ABCD是矩形,
∴AD=CD,∠D=90°,AC=BD,
故A,C,D不符合题意,
当AB=AD时,即一组邻边相等时,矩形ABCD为正方形,
故C符合题意,
故选:B.
4.方程x2﹣6x+4=0的根是( )
A. B. C. D.
【分析】将常数项移到方程的右边,两边都加上一次项系数一半的平方配成完全平方式后,再开方即可得.
解:∵x2﹣6x+4=0,
∴x2﹣6x=﹣4,
∴x2﹣6x+9=﹣4+9,即(x﹣3)2=5,
∴x﹣3=±,
∴x1=3+,x2=3﹣.
故选:C.
5.直角三角形两条直角边长分别是6和8,则斜边上的中线长为( )
A.3 B.4 C.5 D.6
【分析】利用勾股定理求出斜边,再根据直角三角形斜边上的中线等于斜边的一半解答.
解:∵直角三角形两条直角边长分别是6和8,
∴斜边==10,
∴斜边上的中线长=×10=5.
故选:C.
6.如图,在平行四边形ABCD中,DE:EC=4:1,连接AE交BD于点F,则S△DEF:S△BAF为( )
A.3:4 B.9:16 C.16:25 D.4:1
【分析】根据相似三角形的面积比等于相似比的平方即可求解.
解:∵DE:EC=4:1,
∴DE:CD=4:5,
∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,
∴△DEF∽△BAF,
∴,
故选:C.
7.若关于x的方程x2﹣5x+k=0有两个不相等的实数根,则k的取值范围是( )
A. B. C. D.
【分析】利用根的判别式的意义得到Δ=(﹣5)2﹣4k>0,然后解不等式即可.
解:根据题意得Δ=(﹣5)2﹣4k>0,
解得k<.
故选:A.
8.某班学生做“用频率估计概率”的实验时,某一结果出现如图所示的统计图,符合这一结果的实验可能是( )
A.从标有1,2,3,4,5,6的卡片中任抽一张是偶数
B.同时抛掷两枚相同硬币出现的结果是一正一反
C.从一副去掉大小王的扑克中任抽一张牌的花色是红桃
D.掷一个质地均匀的正六面体骰子得到向上的面点数小于3
【分析】根据频率估计概率分别对每一项进行分析,即可得出答案.
解:A、从标有1,2,3,4,5,6的六张卡片中任抽一张,出现偶数的概率是=,不符合这一结果,故此选项不符合题意;
B、同时抛掷两枚相同硬币出现的结果是一正一反的概率是,不符合这一结果,故此选项符合题意;
C、一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率是=0.25,不符合这一结果,故此选项不符合题意;
D、掷一个质地均匀的正六面体骰子得到向上的面点数小于3:=,符合这一结果,故此选项符合题意;
故选:D.
9.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件不能满足△ADE∽△ACB的条件是( )
A.∠AED=∠B B.
C.AD BC=DE AC D.∠ADE=∠C
【分析】根据相似三角形的判定逐一判断即可.
解:∵∠AED=∠B,∠A=∠A,
∴△ADE∽△ACB,
故A正确,不符合题意;
∵,∠A=∠A,
∴△ADE∽△ACB,
故B正确,不符合题意;
∵AD BC=DE AC,
∴,无法判断△ADE∽△ACB,
故C符合题意,
∵∠ADE=∠C,∠A=∠A,
∴△ADE∽△ABC,
故D正确,不符合题意;
故选:C.
10.探索一元二次方程ax2+bx+c=0(a≠0)的一个正数解的过程如表:可以看出方程的一个正数解的取值范围为( )
x ﹣1 0 1 2 3 4
ax2+bx+c ﹣7 ﹣5 ﹣1 5 13 23
A.﹣1<x<0 B.0<x<1 C.1<x<2 D.﹣1<x<5
【分析】根据表格中的数据,可以发现当x=1时,ax2+bx+c=﹣1<0,当x=2时,ax2+bx+c=5>0,从而可以得到整数a、b的值.
解:由表格可得,
当x=1时,ax2+bx+c=﹣1<0,当x=2时,ax2+bx+c=5>0,
∴x2+3x﹣5=0的一个正数解为1和2之间,
即方程的一个正数解的取值范围为1<x<2,
故选:C.
11.若A(﹣2,a),B(1,b),c(2,c)为反比例函数(k为常数)的图象上的三点,则a,b,c的大小关系是( )
A.a<b<c B.c<b<a C.a<c<b D.b<c<a
【分析】根据k的值确定双曲线所在的象限,进而明确函数的增减性,再根据点A(﹣1,a),B(1,b),C(2,c)所在的象限,确定a、b、c大小关系.
解:∵k为常数,
∴k2+1>0,
∴反比例函数(k为常数)的图象位于一三象限,且在每个象限内,y随x的增大而减小,
因此点A(﹣2,a)在第三象限,而B(1,b),C(2,c)在第一象限,
∴a<0,b>c>0,
∴a<c<b,
故选:C.
12.如图,∠ABD=∠CBE=90°,AB=BD,∠CAB=∠E.若BE=10,AD=4,则的值为( )
A. B. C. D.
【分析】先由AB=BD,∠ABD=90°,根据勾股定理求出AB的长为4,再证明△ABC∽△EBD,则===,得出问题的答案.
解:如图,∵AB=BD,∠ABD=90°,
∴AD2=AB2+BD2=2AB2,
∵AD=4,
∴(4)2=2AB2,
∴AB=4,
∵∠CBE=90°,
∴∠ABC=∠DBE=90°﹣∠CBD,
∵∠CAB=∠E,
∴△ABC∽△EBD,
∵BE=10,
∴===,
∴的值为,
故选:D.
二、填空题(5个题,每题4分,共20分)
13.四边形ABCD∽四边形A'B'C'D'.若∠D=90°,∠B'=108°,∠C'=92°,则∠A= 70 °.
【分析】根据相似多边形的对应角相等可得.
解:四边形ABCD∽四边形A′B′C′D′,
则∠B=∠B′=108°,∠C=∠C′=92′
四边形ABCD的内角和是360°,
因而∠A=360°﹣90°﹣108°﹣92°=70°.
故答案为:70.
14.在Rt△ABC中,∠C=90°,BC=2,sinA=,则边AB的长为 8 .
【分析】在直角三角形中,利用∠A的正弦、BC与AB间关系,计算得结论.
解:Rt△ABC中,
∵sinA==,BC=2,
∴AB=2×4=8.
故答案为:8.
15.在一个不透明的布袋里装有1个红球和2个白球,它们除颜色外其余都相同,若先摸出1个球,记下颜色后不放回,再摸出1个球,则两次摸出的球恰好一红一白的概率是 .
【分析】画树状图,共有6种等可能的结果,其中两次摸出的球恰好一红一白的结果有4种,再由概率公式求解即可.
解:画树状图如下:
共有6种等可能的结果,其中两次摸出的球恰好一红一白的结果有4种,
∴两次摸出的球恰好一红一白的概率为=,
故答案为:.
16.某商场出售一批商品,在销售中发现日销售量y(件)与销售价x(元)的变化关系如下表,写出y与x之间的函数关系式 .
售价x(元) 200 240 250 400
日销售量y(件) 30 25 24 15
【分析】根据表格数据可得日销售量y(件)与销售价x(元)的乘积总为6000,则可求得此题结果.
解:由题意得,日销售量y(件)与销售价x(元)的乘积总为6000,
即xy=6000,
变形得,y=,
故答案为:y=.
17.如图,在Rt△ABC中,∠ACB=90°,AC=6,tanA=,将△ABC绕点C顺时针旋转得到△A'B'C,点A的对应点为A',若P为A'B'的中点,连接BP,则线段BP长度的最大值为 4+ .
【分析】连接CP,由勾股定理求出AB=2,由旋转的性质得出A'B'=AB=2,∠A'CB'=∠ACB=90°,由直角三角形的性质求出CP=A'B'=,由题意得出点P在以C为圆心,4为半径的圆上运动,则可求出答案.
解:连接CP,
∵∠ACB=90°,AC=6,tanA=,
∴BC=4,
∴AB===2,
∵将△ABC绕点C旋转,得到△A'B'C,
∴A'B'=AB=2,∠A'CB'=∠ACB=90°,
∵P为A'B′的中点,
∴CP=A'B'=,
∴在旋转的过程中,点P在以C为圆心,4为半径的圆上运动,
∴当B,C,P三点共线时,BP有最大值,
∴BP的最大值为4+.
故答案为:4+.
三、解答题(6个题,共64分)
18.某校园有旗杆AB在阳光下某一时刻的影子长为AG.高1.6米的标杆EF在同一时刻的影子为EM(其中AB,EF都与地面垂直).通过测量获得数据AG=7.5,EM=1米.
(1)在图中画出旗杆的影子;
(2)求旗杆AB的高度.
【分析】(1)根点B作BG∥FM交ZM于点G,线段AG即为所求;
(2)利用相似三角形的性质求解即可.
解:(1)如图,线段AG即为所求;
(2)∵AB,EF在同一时刻的阳光下,
∴BG∥FM,故∠BGA=∠FME.
∵∠BAG=∠FEM=90°,
∴△BAG∽△FEM,
∴=,即=,
∴AB=12(米).
答:旗杆AB的高度为12米.
19.如图,一次函数y=ax+b与反比例函数y=(k≠0)的图象相交于点A(1,﹣3)和B(m,﹣1),连接OA、OB.
(1)求一次函数的解析式;
(2)求△OAB的面积.
【分析】(1)把A点的坐标代入反例函数解析式即可求出反比例函数解析式,进而得出B的坐标,把A、B的坐标代入一次函数解析式即可求出一次函数解析式;
(2)△AOB的面积=△BOD的面积﹣△AOD的面积.
解:(1)∵反比例函数y=(k≠0)的图象经过A(1,﹣3),
∴﹣3=.
∴k=﹣3,
∴反比例函数的表达式为y=﹣.
∵B(m,﹣1)在y=﹣上,
∴m=3.
∴B点坐标为(3,﹣1);
把A,B两点的坐标代入y=ax+b,得,
解得:,
∴一次函数的表达式为:y=x﹣4;
(2)当x=0时,y=﹣4.
∴D点坐标为(0,﹣4).
∴S△AOB=S△BOD﹣S△AOD=﹣=4.
20.如图,在菱形ABCD中,两条对角线相交于点O,F是边CD的中点,连接OF并延长到E,使FE=OF,连接CE,DE.
(1)求证:四边形OCED是矩形;
(2)若∠DAB=60°,菱形ABCD的面积为,求矩形OCED的周长.
【分析】(1)由已知CF=DF,EF=OF,得到四边形OCED是平行四边形,由菱形的性质得到AC⊥BD,即可证得四边形OCED是矩形;
(2)由已知及菱形的性质证得△ABD是等边三角形,由含30度直角三角形的性质得到AD=2OD,设OD=k,则AD=2k,由勾股定理求得AO=k,由菱形的面积公式求出k,进而可求出矩形OCED的周长.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∵CF=DF,EF=OF,
∴四边形OCED是平行四边形,
∵∠DOC=90°,
∴四边形OCED是矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=AD,AC⊥BD,AO=CO,BO=DO,
∵∠DAB=60°,
∴△ABD是等边三角形,
∴AD=BD=AB,∠DAO=∠BAO=30°,
∴AD=2OD,
设OD=k,则AD=2k,
∴BD=2k,
在Rt△AOD中,
AO===k,AC=2k.
∵S菱形ABCD=AC BD,
∴×2k×2k=8,
∴k2=4,
∵k>0,
∴k=2,
∴CO=2,OD=2,
∴矩形OCED的周长=2(OD+OC)=2(2+2)=4+4.
21.某商品的进价是每件40元,当售价每件60元时,当天可售出300件.进行不同程度的涨价后,发现每涨价1元,当天销售量减少10件.设商品售价每件涨价x元(x为正整数)时,当天售出商品的利润为y元.
(1)求y与x之间的函数关系式;
(2)如何定价,才能使商品当天的销售利润达到6250元?
【分析】(1)根据总利润=每件利润×销售量,即可列出函数关系式;
(2)令y=6250,解关于x的方程即可得答案.
解:(1)根据题意得:y=(60+x﹣40)(300﹣10x)
=﹣10x2+100x+6000.
∴y与x之间的函数关系式为y=﹣10x2+100x+6000.
(2)令y=6250,则﹣10x2+100x+6000=6250,
解得x1=x2=5,
此时60+x=60+565(元),
∴当售价为65元时,当天的利润达到6250元.
22.如图,在△ABC中,cos∠BAC=,AB=26,AC=15,BD⊥AC,垂足为D,E是BD的中点,AE与BC交于点F.
(1)求∠CBD的正切值;
(2)求的值.
【分析】(1)由根据余弦的定义以及勾股定理分别求出AD与BD的长,再由AC=15求得CD的长即可求解;
(2)过E作EM∥DC交BC于M,由EM∥CA得△EMF∽△ACF,从而得出比例式求解即可.
解:(1)Rt△ADB中,AB=26,cos∠BAC=,
∴AD=24,
由勾股定理,得BD==10,
∵AC=15,
∴CD=9,
∴tan∠CBD==,
∴∠CBD的正切值为;
(2)过E作EM∥DC交BC于M,
∵E是BD的中点,
∴EM=DC=4.5,DE=5,
∵EM∥CA,
∴△EMF∽△ACF,
∴===,
∴=,
23.在△EFG中,∠EFG=90°,EF=FG,且点E,F分别在矩形ABCD的边AB,AD上,AB=8,AD=6.
(1)如图1,当点G在CD上时,求AE+DG的值;
(2)如图2,FG与CD相交于点N,连接EN,当EF平分∠AEN时,求证:EN=AE+DN;
(3)如图3,EG,FG分别交CD于点M,N,当MG2=MN MD时,求AE的值.
【分析】(1)利用矩形的性质证明△DFG≌△AEF(AAS),得AF=DG,AE=DF,可得答案;
(2)延长NF,EA相交于H,首先利用ASA证明△HFE≌△NFE,得FH=FN,HE=NE,再利用AAS证明△HFA≌△NFD,得AH=DN,可得结论;
(3)过点G作GP⊥AD交AD的延长线于P,利用△MGN∽△MDG,得∠GDM=45°,∠PDG=45°,再利用AAS证明△PFG≌△AEF,得AF=PG,AE=PF即可.
【解答】(1)解:∵四边形ABCD是矩形,
∴∠A=∠D=90°,EF=FG,
∵∠EFG=90°,
∴∠AFE+∠DFN=90°,∠AFE+∠AEF=90°,
∴∠DFN=∠AEF.
∴△DFG≌△AEF(AAS),
∴AF=DG,AE=DF,
∴AE+DG=AF+DF=AD=6;
(2)证明:如图,延长NF,EA相交于H,
∴∠HFE=90°,∠HAF=90°,
∵∠HFE=∠NFE,EF=EF,∠HEF=∠NEF,
∴△HFE≌△NFE(ASA),
∴FH=FN,HE=NE,
∵∠AFH=∠DFN,∠HAF=∠D,
∴△HFA≌△NFD(AAS),
∴AH=DN,
∵EH=AE+AH=AE+DN,
∴EN=AE+DN;
(3)解:如图,过点G作GP⊥AD交AD的延长线于P,
∴∠P=90°,
∵MG2=MN MD,
∴=,
∵∠GMN=∠DMG,
∴△MGN∽△MDG,
∴∠GDM=45°,∠PDG=45°,
∴△PDG是等腰直角三角形,PG=PD,
∵∠AFE+∠PFG=90°,∠AFE+∠AEF=90°,
∴∠PFG=∠AEF,
∵∠A=∠P=90°,EF=FG,
∴△PFG≌△AEF(AAS),
∴AF=PG,AE=PF,
∴AE=PD+DF=AF+DF=AD=6.
同课章节目录
