2021-2022学年青岛版九年级数学下册 第7章 空间图形的初步认识 复习测试(word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版九年级数学下册 第7章 空间图形的初步认识 复习测试(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 397.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 08:27:30 | ||
图片预览


文档简介
复习测试
(时间:120分钟 满分:120分)
一.选择题(每题3分,共30分)
1.下列说法中,正确的个数是( ).
①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体; A.2个 B.3个 C.4个 D.5个
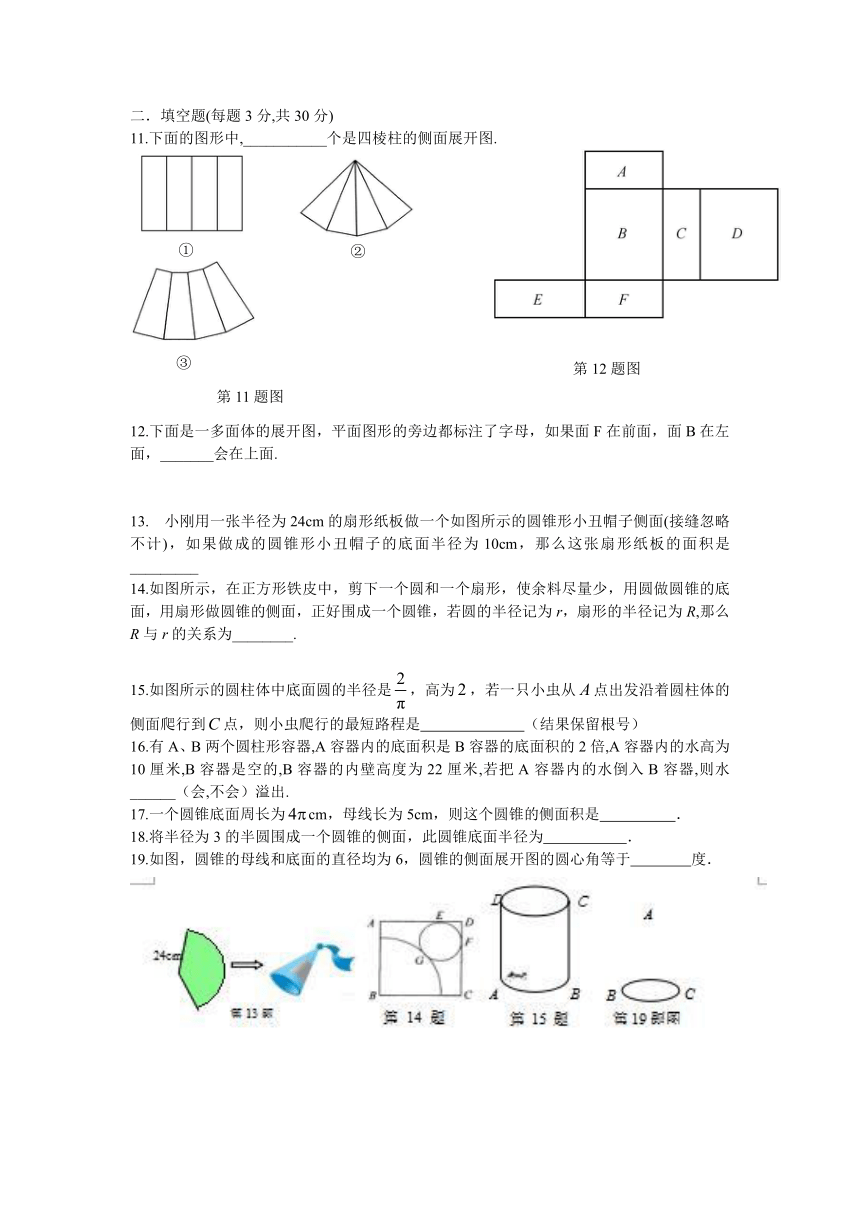
2.小丽制作了一个如下左图所示的正方体礼品盒,其对面图案都相同,那么这个正方体的平面展开图可能是 ( )
3.列图形中,不属于三棱柱的展开图的是 ( )
4.
请根据图中给出的信息,可得正确的方程是( )
A. B.
C. D.
5.将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度与注水时间的函数图象
大致为( )
6.某抗震蓬的顶部是圆锥形,这个圆锥的底面直径为10米,母线长为6米,为了防阴,需要在它的顶部铺上油毡,所需油毡的面积至少是( )
A.30米2 B.60米2 C.30米2 D.60米2
7. 将直径为60cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为( )
A.10cm B.30cm C.45cm D.300cm
8. 如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( ).
A.20cm B.10cm C.14cm (
第5题图
A
.
B
.
C
.
D
.
) D.无法确定
(
第9题图
B
A
Cc
O
第10题图
)
9. 在综合实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面半径高则这个圆锥漏斗的侧面积是( )
A. B. C. D.
10. 已知圆锥的底面半径为5cm,侧面积为cm2,设圆锥的母线与高的夹角为(如图5所示),则的值为( )
A. B.
C. D.
二.填空题(每题3分,共30分)
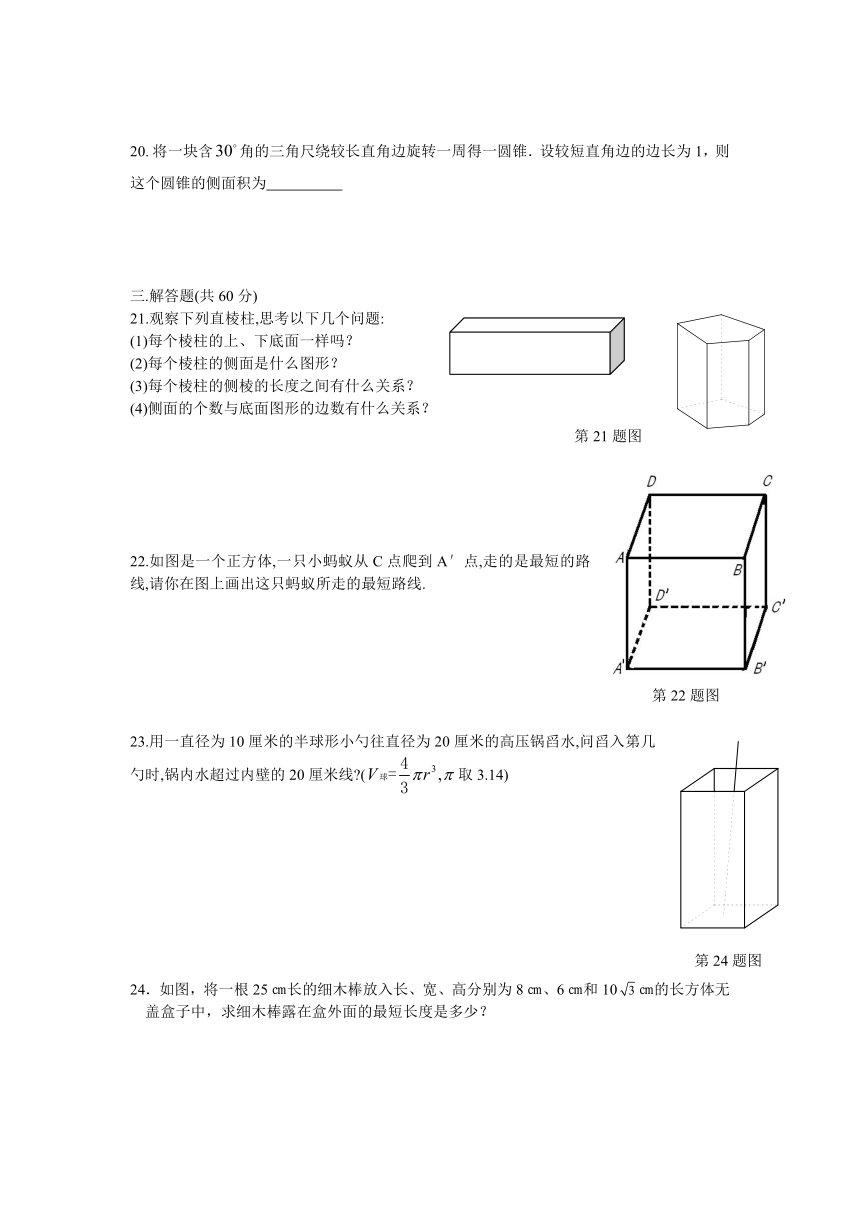
11.下面的图形中,___________个是四棱柱的侧面展开图.
12.下面是一多面体的展开图,平面图形的旁边都标注了字母,如果面F在前面,面B在左面,_______会在上面.
13. 小刚用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的面积是_________
14.如图所示,在正方形铁皮中,剪下一个圆和一个扇形,使余料尽量少,用圆做圆锥的底面,用扇形做圆锥的侧面,正好围成一个圆锥,若圆的半径记为r,扇形的半径记为R,那么R与r的关系为________.
15.如图所示的圆柱体中底面圆的半径是,高为,若一只小虫从点出发沿着圆柱体的侧面爬行到点,则小虫爬行的最短路程是 (结果保留根号)
16.有A、B两个圆柱形容器,A容器内的底面积是B容器的底面积的2倍,A容器内的水高为10厘米,B容器是空的,B容器的内壁高度为22厘米,若把A容器内的水倒入B容器,则水______(会,不会)溢出.
17.一个圆锥底面周长为cm,母线长为5cm,则这个圆锥的侧面积是 .
18.将半径为3的半圆围成一个圆锥的侧面,此圆锥底面半径为 .
19.如图,圆锥的母线和底面的直径均为6,圆锥的侧面展开图的圆心角等于 度.
将一块含角的三角尺绕较长直角边旋转一周得一圆锥.设较短直角边的边长为1,则这个圆锥的侧面积为
三.解答题(共60分)
21.观察下列直棱柱,思考以下几个问题:
(1)每个棱柱的上、下底面一样吗?
(2)每个棱柱的侧面是什么图形?
(3)每个棱柱的侧棱的长度之间有什么关系?
(4)侧面的个数与底面图形的边数有什么关系?
22.如图是一个正方体,一只小蚂蚁从C点爬到A′点,走的是最短的路线,请你在图上画出这只蚂蚁所走的最短路线.
23.用一直径为10厘米的半球形小勺往直径为20厘米的高压锅舀水,问舀入第几勺时,锅内水超过内壁的20厘米线 (取3.14)
24.如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体无盖盒子中,求细木棒露在盒外面的最短长度是多少?
25.如图,一个直角三角形两条直角边分别为3cm和4cm,以斜边所在直线为轴旋转一周得到一个几何体,在虚线框内画出这个几何体的草图,求这个几何体的表面积.
26.在一次数学探究性学习活动中,某学习小组要制作一个圆锥体模型,操作规则是:在一块边长为16cm的正方形纸片上剪出一个扇形和一个圆,使得扇形围成圆锥的侧面时,圆恰好是该圆锥的底面.他们首先设计了如图所示的方案一,发现这种方案不可行,于是他们调整了扇形和圆的半径,设计了如图所示的方案二.(两个方案的图中,圆与正方形相邻两边及扇形的弧均相切.方案一中扇形的弧与正方形的两边相切)
(1)请说明方案一不可行的理由;
(2)判断方案二是否可行?若可行,请确定圆锥的母线长及其底面圆半径;若不可行,请说明理由.
(
方案一
A
B
C
D
方案二
A
B
C
D
·
O
1
·
O
2
第26题图
)
27. 问题探究:
(1)如图①所示是一个半径为,高为4的圆柱体和它的侧面展开图,是圆柱的一条母线,一只蚂蚁从点出发沿圆柱的侧面爬行一周到达点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线剪开,它的侧面展开图如图①中的矩形则蚂蚁爬行的最短路程即为线段的长)
(2)如图②所示是一个底面半径为,母线长为4的圆锥和它的侧面展开图,是它的一条母线,一只蚂蚁从点出发沿圆锥的侧面爬行一周后回到点,求蚂蚁爬行的最短路程.
(3)如图③所示,在②的条件下,一只蚂蚁从点出发沿圆锥的侧面爬行一周到达母线上的一点,求蚂蚁爬行的最短路程.
复习测试
1. B 2. A 3. B 4. A 5. B 6. C 7. A 8. B 9. C 10. B 11. ① 12. C 13. 240πcm2 14. R=4r 15. 16. 不会 17. 18. 19. 180 20. 21. (1)一样 (2)长方形 (3)相等 (4)相等
22.
23. 设舀第勺时锅内水达到内壁20厘米线,由题意得:
故舀入第几25勺时锅内水超过内壁的20厘米线.
24. 5cm
25. 如图作交于,则为两个圆锥共同的底面的半径
(
A
O
C
B
)
以为母线的圆锥侧面积
以为母线的圆锥侧面积
表面积为
26. (1)理由如下:
∵扇形的弧长=16×=8π,圆锥底面周长=2πr,∴圆的半径为4cm.
由于所给正方形纸片的对角线长为cm,而制作这样的圆锥实际需要正方形纸片的对角线长为cm,,
∴方案一不可行.
(2)方案二可行.求解过程如下:
设圆锥底面圆的半径为rcm,圆锥的母线长为Rcm,则
, ① . ②
由①②,可得,.
故所求圆锥的母线长为cm,底面圆的半径为cm.
27. (1)易知
即蚂蚁爬行的最短路程为5.
(2)连结则的长为蚂蚁爬行的最短路程,设为圆锥底面半径,为侧面展开图(扇形)的半径,则由题意得:
即
是等边三角形
最短路程为
(3)如图③所示是圆锥的侧面展开图,过作于点则线段的长就是蚂蚁爬行的最短路程.
蚂蚁爬行的最短距离为
(
B
A
图①
图③
P
C
A
60
°
图②
P
A
)
(时间:120分钟 满分:120分)
一.选择题(每题3分,共30分)
1.下列说法中,正确的个数是( ).
①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体; A.2个 B.3个 C.4个 D.5个
2.小丽制作了一个如下左图所示的正方体礼品盒,其对面图案都相同,那么这个正方体的平面展开图可能是 ( )
3.列图形中,不属于三棱柱的展开图的是 ( )
4.
请根据图中给出的信息,可得正确的方程是( )
A. B.
C. D.
5.将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度与注水时间的函数图象
大致为( )
6.某抗震蓬的顶部是圆锥形,这个圆锥的底面直径为10米,母线长为6米,为了防阴,需要在它的顶部铺上油毡,所需油毡的面积至少是( )
A.30米2 B.60米2 C.30米2 D.60米2
7. 将直径为60cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为( )
A.10cm B.30cm C.45cm D.300cm
8. 如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( ).
A.20cm B.10cm C.14cm (
第5题图
A
.
B
.
C
.
D
.
) D.无法确定
(
第9题图
B
A
Cc
O
第10题图
)
9. 在综合实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面半径高则这个圆锥漏斗的侧面积是( )
A. B. C. D.
10. 已知圆锥的底面半径为5cm,侧面积为cm2,设圆锥的母线与高的夹角为(如图5所示),则的值为( )
A. B.
C. D.
二.填空题(每题3分,共30分)
11.下面的图形中,___________个是四棱柱的侧面展开图.
12.下面是一多面体的展开图,平面图形的旁边都标注了字母,如果面F在前面,面B在左面,_______会在上面.
13. 小刚用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的面积是_________
14.如图所示,在正方形铁皮中,剪下一个圆和一个扇形,使余料尽量少,用圆做圆锥的底面,用扇形做圆锥的侧面,正好围成一个圆锥,若圆的半径记为r,扇形的半径记为R,那么R与r的关系为________.
15.如图所示的圆柱体中底面圆的半径是,高为,若一只小虫从点出发沿着圆柱体的侧面爬行到点,则小虫爬行的最短路程是 (结果保留根号)
16.有A、B两个圆柱形容器,A容器内的底面积是B容器的底面积的2倍,A容器内的水高为10厘米,B容器是空的,B容器的内壁高度为22厘米,若把A容器内的水倒入B容器,则水______(会,不会)溢出.
17.一个圆锥底面周长为cm,母线长为5cm,则这个圆锥的侧面积是 .
18.将半径为3的半圆围成一个圆锥的侧面,此圆锥底面半径为 .
19.如图,圆锥的母线和底面的直径均为6,圆锥的侧面展开图的圆心角等于 度.
将一块含角的三角尺绕较长直角边旋转一周得一圆锥.设较短直角边的边长为1,则这个圆锥的侧面积为
三.解答题(共60分)
21.观察下列直棱柱,思考以下几个问题:
(1)每个棱柱的上、下底面一样吗?
(2)每个棱柱的侧面是什么图形?
(3)每个棱柱的侧棱的长度之间有什么关系?
(4)侧面的个数与底面图形的边数有什么关系?
22.如图是一个正方体,一只小蚂蚁从C点爬到A′点,走的是最短的路线,请你在图上画出这只蚂蚁所走的最短路线.
23.用一直径为10厘米的半球形小勺往直径为20厘米的高压锅舀水,问舀入第几勺时,锅内水超过内壁的20厘米线 (取3.14)
24.如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体无盖盒子中,求细木棒露在盒外面的最短长度是多少?
25.如图,一个直角三角形两条直角边分别为3cm和4cm,以斜边所在直线为轴旋转一周得到一个几何体,在虚线框内画出这个几何体的草图,求这个几何体的表面积.
26.在一次数学探究性学习活动中,某学习小组要制作一个圆锥体模型,操作规则是:在一块边长为16cm的正方形纸片上剪出一个扇形和一个圆,使得扇形围成圆锥的侧面时,圆恰好是该圆锥的底面.他们首先设计了如图所示的方案一,发现这种方案不可行,于是他们调整了扇形和圆的半径,设计了如图所示的方案二.(两个方案的图中,圆与正方形相邻两边及扇形的弧均相切.方案一中扇形的弧与正方形的两边相切)
(1)请说明方案一不可行的理由;
(2)判断方案二是否可行?若可行,请确定圆锥的母线长及其底面圆半径;若不可行,请说明理由.
(
方案一
A
B
C
D
方案二
A
B
C
D
·
O
1
·
O
2
第26题图
)
27. 问题探究:
(1)如图①所示是一个半径为,高为4的圆柱体和它的侧面展开图,是圆柱的一条母线,一只蚂蚁从点出发沿圆柱的侧面爬行一周到达点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线剪开,它的侧面展开图如图①中的矩形则蚂蚁爬行的最短路程即为线段的长)
(2)如图②所示是一个底面半径为,母线长为4的圆锥和它的侧面展开图,是它的一条母线,一只蚂蚁从点出发沿圆锥的侧面爬行一周后回到点,求蚂蚁爬行的最短路程.
(3)如图③所示,在②的条件下,一只蚂蚁从点出发沿圆锥的侧面爬行一周到达母线上的一点,求蚂蚁爬行的最短路程.
复习测试
1. B 2. A 3. B 4. A 5. B 6. C 7. A 8. B 9. C 10. B 11. ① 12. C 13. 240πcm2 14. R=4r 15. 16. 不会 17. 18. 19. 180 20. 21. (1)一样 (2)长方形 (3)相等 (4)相等
22.
23. 设舀第勺时锅内水达到内壁20厘米线,由题意得:
故舀入第几25勺时锅内水超过内壁的20厘米线.
24. 5cm
25. 如图作交于,则为两个圆锥共同的底面的半径
(
A
O
C
B
)
以为母线的圆锥侧面积
以为母线的圆锥侧面积
表面积为
26. (1)理由如下:
∵扇形的弧长=16×=8π,圆锥底面周长=2πr,∴圆的半径为4cm.
由于所给正方形纸片的对角线长为cm,而制作这样的圆锥实际需要正方形纸片的对角线长为cm,,
∴方案一不可行.
(2)方案二可行.求解过程如下:
设圆锥底面圆的半径为rcm,圆锥的母线长为Rcm,则
, ① . ②
由①②,可得,.
故所求圆锥的母线长为cm,底面圆的半径为cm.
27. (1)易知
即蚂蚁爬行的最短路程为5.
(2)连结则的长为蚂蚁爬行的最短路程,设为圆锥底面半径,为侧面展开图(扇形)的半径,则由题意得:
即
是等边三角形
最短路程为
(3)如图③所示是圆锥的侧面展开图,过作于点则线段的长就是蚂蚁爬行的最短路程.
蚂蚁爬行的最短距离为
(
B
A
图①
图③
P
C
A
60
°
图②
P
A
)
