2021-2022学年青岛版九年级数学下册第五章 对函数的再探究 单元检测试卷(word版、含答案)
文档属性
| 名称 | 2021-2022学年青岛版九年级数学下册第五章 对函数的再探究 单元检测试卷(word版、含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 115.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 09:42:58 | ||
图片预览


文档简介
对函数的再探究 单元检测试卷
一、单选题(共10题;共30分)
1.反比例函数y=﹣ 的图象在( )
A. 第一、三象限 B. 第一、二象限 C. 第二、四象限 D. 第三、四象限
2.如图,
已知抛物线y=x2-bx+c的对称轴为x=2,点A , B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为
A. (2,3) B. (3,2) C. (3,3) D. (4,3)
3.如图坐标平面上有一透明片,透明片上有一拋物线及一点P , 且拋物线为二次函数y=x2的图形,P的坐标(2,4)。若将此透明片向右、向上移动后,得拋物线的顶点坐标为(7,2),则此时P的坐标为 ( )
A. (9,4) B. (9,6) C. (10,4) D. (10,6)
4.已知反比例函数的图象经过点(﹣1,2),则它的解析式是( )
A. y=﹣ B. y=﹣ C. y= D. y=
5.把抛物线 的图象向左平移1个单位,再向上平移6个单位,所得的抛物线的函数关系式是( )
A. B.
C. D.
6.已知抛物线y=ax2+bx+c如图所示,则下列结论中,正确的是( )
A. a>0 B. a-b+c>0 C. b2-4ac<0 D. 2a+b=0
7.根据科学研究表明,在弹簧的承受范围内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下表的关系:下列说法不正确的是( )
x/kg 0 1 2 3 4 5
y/cm 20 20.5 21 21.5 22 22.5
A.弹簧不挂重物时的长度为0cm
B.x与y都是变量,且x是自变量,y是因变量
C.随着所挂物体的重量增加,弹簧长度逐渐边长
D.所挂物体的重量每增加1kg,弹簧长度增加0.5cm
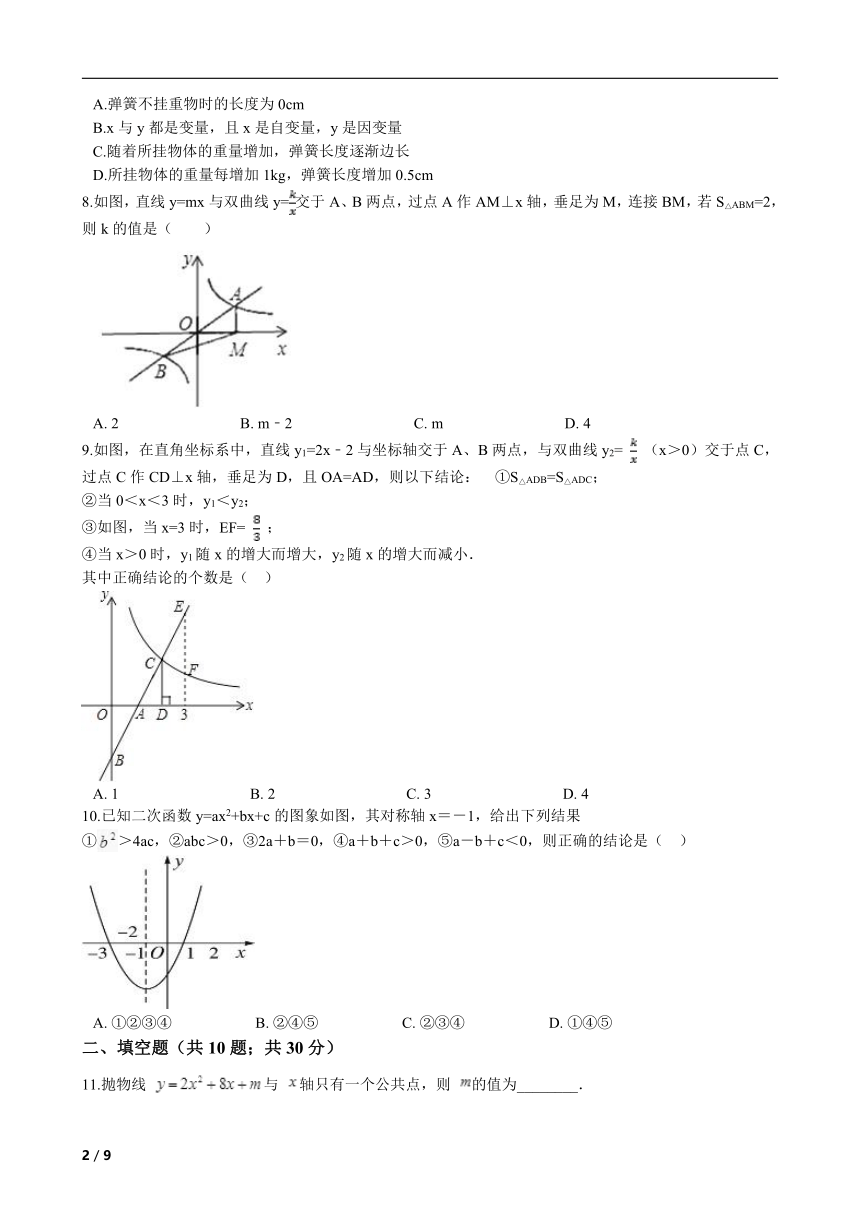
8.如图,直线y=mx与双曲线y=交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=2,则k的值是( )
A. 2 B. m﹣2 C. m D. 4
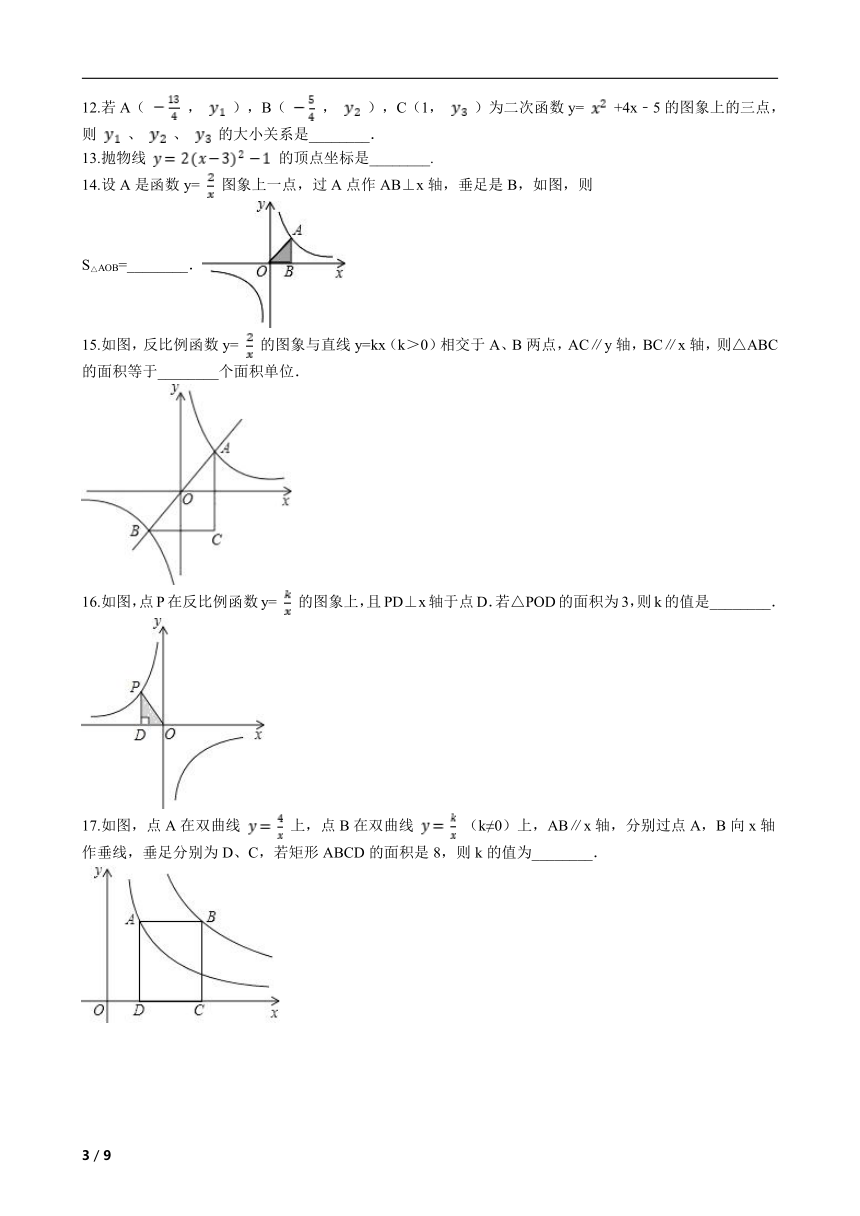
9.如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2= (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论: ①S△ADB=S△ADC;
②当0<x<3时,y1<y2;
③如图,当x=3时,EF= ;
④当x>0时,y1随x的增大而增大,y2随x的增大而减小.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
10.已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果
①>4ac,②abc>0,③2a+b=0,④a+b+c>0,⑤a-b+c<0,则正确的结论是( )
A. ①②③④ B. ②④⑤ C. ②③④ D. ①④⑤
二、填空题(共10题;共30分)
11.抛物线 与 轴只有一个公共点,则 的值为________.
12.若A( , ),B( , ),C(1, )为二次函数y= +4x﹣5的图象上的三点,则 、 、 的大小关系是________.
13.抛物线 的顶点坐标是________.
14.设A是函数y= 图象上一点,过A点作AB⊥x轴,垂足是B,如图,则S△AOB=________.
15.如图,反比例函数y= 的图象与直线y=kx(k>0)相交于A、B两点,AC∥y轴,BC∥x轴,则△ABC的面积等于________个面积单位.
16.如图,点P在反比例函数y= 的图象上,且PD⊥x轴于点D.若△POD的面积为3,则k的值是________.
17.如图,点A在双曲线 上,点B在双曲线 (k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为________.
18.如图,已知函数y=﹣与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+=0的解是________
19.竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t=________.
20.如图,在平面直角坐标系中,反比例函数 (x>0)与正比例函数y=kx、 (k>1)的图像分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
三、解答题(共7题;共60分)
21.如图,等腰梯形的周长为60,底角为30°,腰长为x,面积为y,试写出y与x的函数表达式.
22.已知:二次函数y=(n﹣1)x2+2mx+1图象的顶点在x轴上.
(1)请写出m与n的关系式,并判断已知中函数图象的开口方向;
(2)是否存在整数m,n的值,使函数图象的对称轴与x轴的交点横坐标为整数?若存在,请求出m,n的值;若不存在,请说明理由;
(3)若y关于x的函数关系式为y=nx2﹣m2x﹣2n﹣2
①当n≠0时,求该函数必过的定点坐标;
②探索这个函数图象与坐标轴有两个交点时n的值.
23.如图,已知抛物线y=ax2+bx+3的图象与x轴交于A、B两点,与y轴交于点C,且点C、D是抛物线上的一对对称点
(1)求抛物线的解析式
(2)求点D的坐标,并在图中画出直线BD
(3)求出直线BD的一次函数解析式,并根据图象回答:当x满足什么条件时,上述二次函数的值大于该一次函数的值
24.某商人如果将进货单价为8元的商品按每件10元出售,每天可售出100件,现在他采用提高售出价,减少进货量的办法增加利润,已知这种商品每提高1元,其销售量就要减少10件,如果他每天所赚利润为y元,试求出y与售出价x之间的函数关系式.
25.如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.
26.如图,边长为2的正方形ABCD的中心在直角坐标系的原点O,AD∥x轴,以O为顶点且过A、D两点的抛物线与以O为顶点且过B、C两点的抛物线将正方形分割成几部分.则图中阴影部分的面积是多少?
27.如图,抛物线 与 轴交于 、 两点(点 在点 的左侧),点 的坐标为 ,与 轴交于点 ,作直线 .动点 在 轴上运动,过点 作 轴,交抛物线于点 ,交直线 于点 ,设点 的横坐标为 .
(Ⅰ)求抛物线的解析式和直线 的解析式;
(Ⅱ)当点 在线段 上运动时,求线段 的最大值;
(Ⅲ)当以 、 、 、 为顶点的四边形是平行四边形时,直接写出 的值.
答案解析部分
一、单选题
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】A
8.【答案】A
9.【答案】C
10.【答案】D
二、填空题
11.【答案】8
12.【答案】 < <
13.【答案】(3,-1)
14.【答案】1
15.【答案】4
16.【答案】﹣6
17.【答案】12
18.【答案】x=﹣3
19.【答案】1.6
20.【答案】2
三、解答题
21.【答案】解:作AE⊥BC, 在Rt△ABE中,∠B=30°,
则AE= AB= x,
∵四边形ABCD是等腰梯形,
∴AD+BC=60﹣AB﹣CD=60﹣2x,
∴S= (AD+BC)×AE= (60﹣2x)× x=﹣ x2+15x(0<x<60).
22.【答案】解:(1)∵二次函数y=(n﹣1)x2+2mx+1图象的顶点在x轴上,
∴4m2﹣4(n﹣1)=0,
∴n﹣1=m2 ,
∴n=m2+1,
∵n﹣1≠0,且m2≥0
∴n﹣1>0,
∴图象开口向上;
(2)∵y=(n﹣1)x2+2mx+1,
∴对称轴x=,
要使为整数,
∵m,n为整数,
∴只要m=±1,此时n=2,
∴存在m=±1,n=2,符合要求;
(3)①y=nx2﹣(n﹣1)x﹣2n﹣2=n(x2﹣x﹣2)+x﹣2,
令x2﹣x﹣2=0,得x=﹣1或2,所以必过的定点为(2,0),(﹣1,﹣3),
②若n=0,则y=x﹣2,直线与坐标轴有两个交点,
若n≠0:b2﹣4ac=(n﹣1)2+4n(2n+2)=(3n+1)2≥0,
当抛物线过原点时,n=﹣1,此时图象与坐标轴有两个交点,
当抛物线不过原点时,n=时,b2﹣4ac=0,图象与x轴,y轴各有1个交点,
综上,当n=0或﹣1或时,函数图象与坐标轴有两个交点.
23.【答案】解:(1)二次函数y=ax2+bx+3的图象经过点A(-3,0),B(1,0)
∴9a-3b+3="0" ,a+b+3=0;解得a=-1 、b=-2;
∴二次函数图象的解析式为y=-x2-2x+3;
(2)∵y=-x2-2x+3,
∴图象与y轴的交点坐标为(0,3)
∵点C、D是抛物线上的一对对称点.对称轴x=-b/2a=-1,
∴D点的坐标为(-2,3).
(3)设直线BD的一次函数解析式为y=kx+b
把B(1,0),D(-2,3)分别代入得:0=k+b、3=-2k+b
解得:k=-1,b=1。
∴BD的解析式为y=-x+1。
由图象可知二次函数的值大于该一次函数的值时:-2<x<1。
24.【答案】解:由题意得:每件利润为(x﹣8)元,销量为[100﹣10(x﹣10)]件, 所以y=(x﹣8) [100﹣10(x﹣10)]=﹣10x2+280x﹣1600(10≤x<20)
25.【答案】解:△PBQ的面积S随出发时间t(s)成二次函数关系变化, ∵在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,
动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,
∴BP=12﹣2t,BQ=4t,
∴△PBQ的面积S随出发时间t(s)的解析式为:y= (12﹣2t)×4t=﹣4t2+24t,(0<t<6)
26.【答案】解:由图象知,图中两个二次函数关于x轴对称,故把x轴下半部分阴影部分面积移到x轴上半部分,则所有的阴影部分面积是半个正方形的面积,故为2.
27.【答案】解:(I)∵抛物线过A、C两点,
∴代入抛物线解析式可得 ,解得 ,
∴抛物线解析式为y=﹣x2+2x+3,
令y=0可得,﹣x2+2x+3=0,解x1=﹣1,x2=3,
∵B点在A点右侧,
∴B点坐标为(3,0),
设直线BC解析式为y=kx+s,
把B、C坐标代入可得 ,解得 ,
∴直线BC解析式为y=﹣x+3;
(Ⅱ)∵PM⊥x轴,点P的横坐标为m,
∴M(m,﹣m2+2m+3),N(m,- m+3),
∵P在线段OB上运动,
∴M点在N点上方,
∴MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣ )2+ ,
∴当m= 时,MN有最大值,MN的最大值为 ;
(Ⅲ)∵PM⊥x轴,
∴MN∥OC,
当以C、O、M、N为顶点的四边形是平行四边形时,则有OC=MN,
当点P在线段OB上时,则有MN=﹣m2+3m,
∴﹣m2+3m=3,此方程无实数根,
当点P不在线段OB上时,则有MN=﹣m+3﹣(﹣m2+2m+3)=m2﹣3m,
∴m2﹣3m=3,解得m= 或m= ,
综上可知当以C、O、M、N为顶点的四边形是平行四边形时,m的值为 或
第11页 共18页 ◎ 第12页 共18页
7 / 9
一、单选题(共10题;共30分)
1.反比例函数y=﹣ 的图象在( )
A. 第一、三象限 B. 第一、二象限 C. 第二、四象限 D. 第三、四象限
2.如图,
已知抛物线y=x2-bx+c的对称轴为x=2,点A , B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为
A. (2,3) B. (3,2) C. (3,3) D. (4,3)
3.如图坐标平面上有一透明片,透明片上有一拋物线及一点P , 且拋物线为二次函数y=x2的图形,P的坐标(2,4)。若将此透明片向右、向上移动后,得拋物线的顶点坐标为(7,2),则此时P的坐标为 ( )
A. (9,4) B. (9,6) C. (10,4) D. (10,6)
4.已知反比例函数的图象经过点(﹣1,2),则它的解析式是( )
A. y=﹣ B. y=﹣ C. y= D. y=
5.把抛物线 的图象向左平移1个单位,再向上平移6个单位,所得的抛物线的函数关系式是( )
A. B.
C. D.
6.已知抛物线y=ax2+bx+c如图所示,则下列结论中,正确的是( )
A. a>0 B. a-b+c>0 C. b2-4ac<0 D. 2a+b=0
7.根据科学研究表明,在弹簧的承受范围内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下表的关系:下列说法不正确的是( )
x/kg 0 1 2 3 4 5
y/cm 20 20.5 21 21.5 22 22.5
A.弹簧不挂重物时的长度为0cm
B.x与y都是变量,且x是自变量,y是因变量
C.随着所挂物体的重量增加,弹簧长度逐渐边长
D.所挂物体的重量每增加1kg,弹簧长度增加0.5cm
8.如图,直线y=mx与双曲线y=交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=2,则k的值是( )
A. 2 B. m﹣2 C. m D. 4
9.如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2= (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论: ①S△ADB=S△ADC;
②当0<x<3时,y1<y2;
③如图,当x=3时,EF= ;
④当x>0时,y1随x的增大而增大,y2随x的增大而减小.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
10.已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果
①>4ac,②abc>0,③2a+b=0,④a+b+c>0,⑤a-b+c<0,则正确的结论是( )
A. ①②③④ B. ②④⑤ C. ②③④ D. ①④⑤
二、填空题(共10题;共30分)
11.抛物线 与 轴只有一个公共点,则 的值为________.
12.若A( , ),B( , ),C(1, )为二次函数y= +4x﹣5的图象上的三点,则 、 、 的大小关系是________.
13.抛物线 的顶点坐标是________.
14.设A是函数y= 图象上一点,过A点作AB⊥x轴,垂足是B,如图,则S△AOB=________.
15.如图,反比例函数y= 的图象与直线y=kx(k>0)相交于A、B两点,AC∥y轴,BC∥x轴,则△ABC的面积等于________个面积单位.
16.如图,点P在反比例函数y= 的图象上,且PD⊥x轴于点D.若△POD的面积为3,则k的值是________.
17.如图,点A在双曲线 上,点B在双曲线 (k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为________.
18.如图,已知函数y=﹣与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+=0的解是________
19.竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t=________.
20.如图,在平面直角坐标系中,反比例函数 (x>0)与正比例函数y=kx、 (k>1)的图像分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
三、解答题(共7题;共60分)
21.如图,等腰梯形的周长为60,底角为30°,腰长为x,面积为y,试写出y与x的函数表达式.
22.已知:二次函数y=(n﹣1)x2+2mx+1图象的顶点在x轴上.
(1)请写出m与n的关系式,并判断已知中函数图象的开口方向;
(2)是否存在整数m,n的值,使函数图象的对称轴与x轴的交点横坐标为整数?若存在,请求出m,n的值;若不存在,请说明理由;
(3)若y关于x的函数关系式为y=nx2﹣m2x﹣2n﹣2
①当n≠0时,求该函数必过的定点坐标;
②探索这个函数图象与坐标轴有两个交点时n的值.
23.如图,已知抛物线y=ax2+bx+3的图象与x轴交于A、B两点,与y轴交于点C,且点C、D是抛物线上的一对对称点
(1)求抛物线的解析式
(2)求点D的坐标,并在图中画出直线BD
(3)求出直线BD的一次函数解析式,并根据图象回答:当x满足什么条件时,上述二次函数的值大于该一次函数的值
24.某商人如果将进货单价为8元的商品按每件10元出售,每天可售出100件,现在他采用提高售出价,减少进货量的办法增加利润,已知这种商品每提高1元,其销售量就要减少10件,如果他每天所赚利润为y元,试求出y与售出价x之间的函数关系式.
25.如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.
26.如图,边长为2的正方形ABCD的中心在直角坐标系的原点O,AD∥x轴,以O为顶点且过A、D两点的抛物线与以O为顶点且过B、C两点的抛物线将正方形分割成几部分.则图中阴影部分的面积是多少?
27.如图,抛物线 与 轴交于 、 两点(点 在点 的左侧),点 的坐标为 ,与 轴交于点 ,作直线 .动点 在 轴上运动,过点 作 轴,交抛物线于点 ,交直线 于点 ,设点 的横坐标为 .
(Ⅰ)求抛物线的解析式和直线 的解析式;
(Ⅱ)当点 在线段 上运动时,求线段 的最大值;
(Ⅲ)当以 、 、 、 为顶点的四边形是平行四边形时,直接写出 的值.
答案解析部分
一、单选题
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】A
8.【答案】A
9.【答案】C
10.【答案】D
二、填空题
11.【答案】8
12.【答案】 < <
13.【答案】(3,-1)
14.【答案】1
15.【答案】4
16.【答案】﹣6
17.【答案】12
18.【答案】x=﹣3
19.【答案】1.6
20.【答案】2
三、解答题
21.【答案】解:作AE⊥BC, 在Rt△ABE中,∠B=30°,
则AE= AB= x,
∵四边形ABCD是等腰梯形,
∴AD+BC=60﹣AB﹣CD=60﹣2x,
∴S= (AD+BC)×AE= (60﹣2x)× x=﹣ x2+15x(0<x<60).
22.【答案】解:(1)∵二次函数y=(n﹣1)x2+2mx+1图象的顶点在x轴上,
∴4m2﹣4(n﹣1)=0,
∴n﹣1=m2 ,
∴n=m2+1,
∵n﹣1≠0,且m2≥0
∴n﹣1>0,
∴图象开口向上;
(2)∵y=(n﹣1)x2+2mx+1,
∴对称轴x=,
要使为整数,
∵m,n为整数,
∴只要m=±1,此时n=2,
∴存在m=±1,n=2,符合要求;
(3)①y=nx2﹣(n﹣1)x﹣2n﹣2=n(x2﹣x﹣2)+x﹣2,
令x2﹣x﹣2=0,得x=﹣1或2,所以必过的定点为(2,0),(﹣1,﹣3),
②若n=0,则y=x﹣2,直线与坐标轴有两个交点,
若n≠0:b2﹣4ac=(n﹣1)2+4n(2n+2)=(3n+1)2≥0,
当抛物线过原点时,n=﹣1,此时图象与坐标轴有两个交点,
当抛物线不过原点时,n=时,b2﹣4ac=0,图象与x轴,y轴各有1个交点,
综上,当n=0或﹣1或时,函数图象与坐标轴有两个交点.
23.【答案】解:(1)二次函数y=ax2+bx+3的图象经过点A(-3,0),B(1,0)
∴9a-3b+3="0" ,a+b+3=0;解得a=-1 、b=-2;
∴二次函数图象的解析式为y=-x2-2x+3;
(2)∵y=-x2-2x+3,
∴图象与y轴的交点坐标为(0,3)
∵点C、D是抛物线上的一对对称点.对称轴x=-b/2a=-1,
∴D点的坐标为(-2,3).
(3)设直线BD的一次函数解析式为y=kx+b
把B(1,0),D(-2,3)分别代入得:0=k+b、3=-2k+b
解得:k=-1,b=1。
∴BD的解析式为y=-x+1。
由图象可知二次函数的值大于该一次函数的值时:-2<x<1。
24.【答案】解:由题意得:每件利润为(x﹣8)元,销量为[100﹣10(x﹣10)]件, 所以y=(x﹣8) [100﹣10(x﹣10)]=﹣10x2+280x﹣1600(10≤x<20)
25.【答案】解:△PBQ的面积S随出发时间t(s)成二次函数关系变化, ∵在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,
动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,
∴BP=12﹣2t,BQ=4t,
∴△PBQ的面积S随出发时间t(s)的解析式为:y= (12﹣2t)×4t=﹣4t2+24t,(0<t<6)
26.【答案】解:由图象知,图中两个二次函数关于x轴对称,故把x轴下半部分阴影部分面积移到x轴上半部分,则所有的阴影部分面积是半个正方形的面积,故为2.
27.【答案】解:(I)∵抛物线过A、C两点,
∴代入抛物线解析式可得 ,解得 ,
∴抛物线解析式为y=﹣x2+2x+3,
令y=0可得,﹣x2+2x+3=0,解x1=﹣1,x2=3,
∵B点在A点右侧,
∴B点坐标为(3,0),
设直线BC解析式为y=kx+s,
把B、C坐标代入可得 ,解得 ,
∴直线BC解析式为y=﹣x+3;
(Ⅱ)∵PM⊥x轴,点P的横坐标为m,
∴M(m,﹣m2+2m+3),N(m,- m+3),
∵P在线段OB上运动,
∴M点在N点上方,
∴MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣ )2+ ,
∴当m= 时,MN有最大值,MN的最大值为 ;
(Ⅲ)∵PM⊥x轴,
∴MN∥OC,
当以C、O、M、N为顶点的四边形是平行四边形时,则有OC=MN,
当点P在线段OB上时,则有MN=﹣m2+3m,
∴﹣m2+3m=3,此方程无实数根,
当点P不在线段OB上时,则有MN=﹣m+3﹣(﹣m2+2m+3)=m2﹣3m,
∴m2﹣3m=3,解得m= 或m= ,
综上可知当以C、O、M、N为顶点的四边形是平行四边形时,m的值为 或
第11页 共18页 ◎ 第12页 共18页
7 / 9
