2021-2022学年华东师大版数学九年级下册26.1 二次函数 单元练习一-(word版、含答案)
文档属性
| 名称 | 2021-2022学年华东师大版数学九年级下册26.1 二次函数 单元练习一-(word版、含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 372.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 09:47:46 | ||
图片预览





文档简介
二次函数单元练习一
1.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
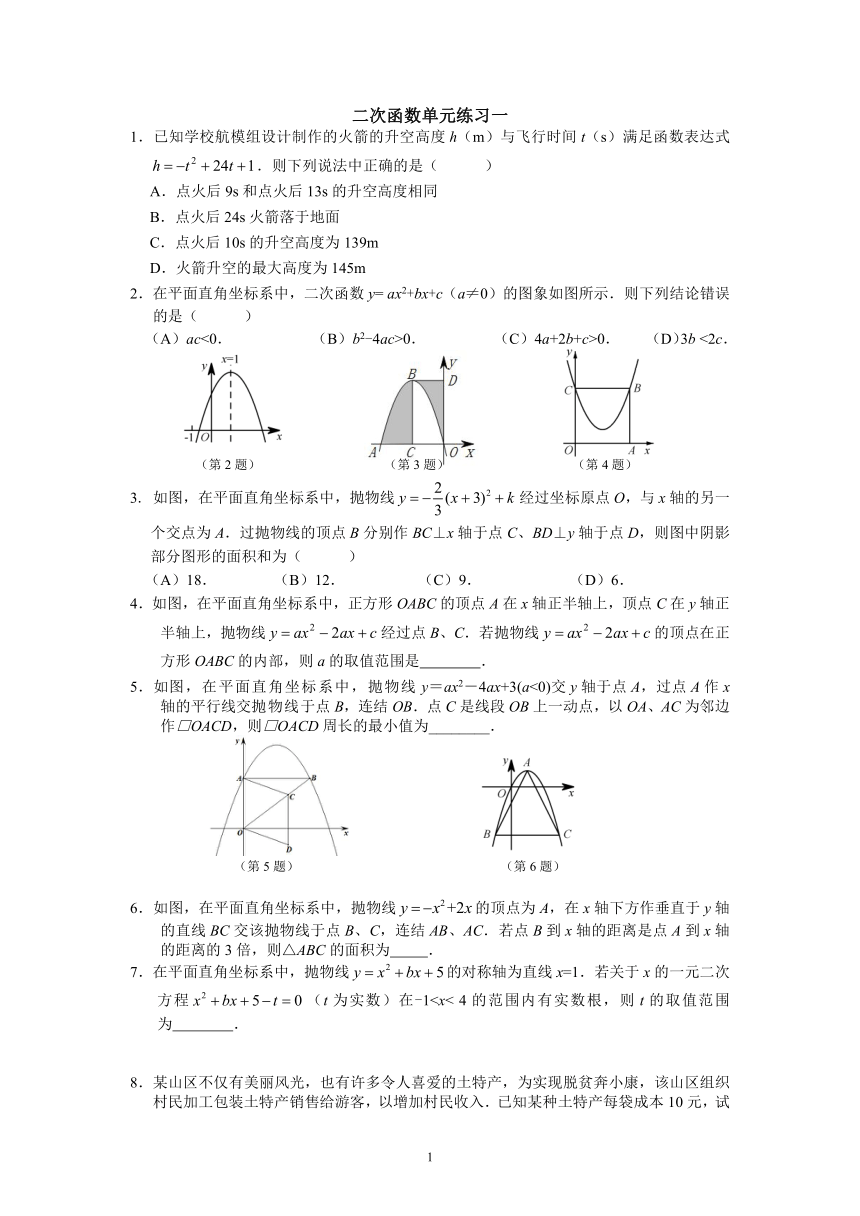
2.在平面直角坐标系中,二次函数y= ax2+bx+c(a≠0)的图象如图所示.则下列结论错误的是( )
(A)ac<0. (B)b2-4ac>0. (C)4a+2b+c>0. (D)3b <2c.
3. 如图,在平面直角坐标系中,抛物线经过坐标原点O,与x轴的另一个交点为A.过抛物线的顶点B分别作BC⊥x轴于点C、BD⊥y轴于点D,则图中阴影部分图形的面积和为( )
(A)18. (B)12. (C)9. (D)6.
4.如图,在平面直角坐标系中,正方形OABC的顶点A在x轴正半轴上,顶点C在y轴正半轴上,抛物线经过点B、C.若抛物线的顶点在正方形OABC的内部,则a的取值范围是 .
5.如图,在平面直角坐标系中,抛物线y=ax2-4ax+3(a<0)交y轴于点A,过点A作x轴的平行线交抛物线于点B,连结OB.点C是线段OB上一动点,以OA、AC为邻边作□OACD,则□OACD周长的最小值为________.
6.如图,在平面直角坐标系中,抛物线的顶点为A,在x轴下方作垂直于y轴的直线BC交该抛物线于点B、C,连结AB、AC.若点B到x轴的距离是点A到x轴的距离的3倍,则△ABC的面积为 .
7.在平面直角坐标系中,抛物线的对称轴为直线x=1.若关于x的一元二次方程(t为实数)在-18.某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,该山区组织村民加工包装土特产销售给游客,以增加村民收入.已知某种土特产每袋成本10元,试销阶段每袋的销售价x(元)与该土特产的日销售量y(袋)之间的关系如下表:
x(元) 15 20 30 …
y(袋) 25 20 10 …
(1)若日销售量y(袋)是销售价x(元)的一次函数,求y与x之间的函数表达式.
(2)假设后续销售情况与试销阶段效果相同,设每日销售土特产的利润为w(元).
①求w与x之间的函数表达式.
②要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元 每日销售的最大利润是多少元
9.已知抛物线与x轴交于点A和B,第一象限内的点C在该抛物线上.
(1)直接写出A、B两点的坐标.
(2)若△ABC的面积为12,求点C坐标.
(3)在(2)问的条件下,直线经过点A、C.当>时,直接写出x的取值范围.
10.如图①,一个横截面为抛物线形的隧道,其底部的宽AB为8 m,拱高为4 m.该隧道为双向车道,且两车道之间有0.4 m的隔离带.一辆宽为2 m的货车要安全通过这条隧道,需保持其顶部与隧道有不少于0.5 m的空隙.按如图②所示建立平面直角坐标系.
(1)求该抛物线对应的函数关系式.
(2)通过计算说明该货车能够安全通行的最大高度.
11.如图,隧道的横截面由抛物线形和矩形OABC构成.矩形一边OA的长是12m,另一边OC的长是1m.抛物线上的最高点D到地面OA的距离为7m.以OA所在直线为x轴,以OC所在直线为y轴,建立平面直角坐标系.
(1)求该抛物线所对应的函数表达式.
(2)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度为5m,求两排灯之间的水平距离.
(3)隧道内车辆双向通行,规定车辆必须在中心线两侧行驶,并保持车辆顶部与隧道有不少于m的空隙.现有一辆货运汽车,在隧道内距离道路边缘2m处行驶,求这辆货运汽车载物后的最大高度.
(第11题)
12.某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合,如图所示,以水平方向为x轴,喷水池中心为原点建立平面直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
13.在平面直角坐标系中,抛物线经过点(6,7),其对称轴为直线x=2.
(1)求这条抛物线所对应的函数表达式.
(2)当时,求函数值y的取值范围.
(3)当时,函数值y先随x的增大而减小,后随x的增大而增大,且y的最大值为7,则k的取值范围是 .
(4)已知A、B两点均在抛物线上,点A的横坐标为m,点B的横坐标为m+2.将抛物线上A、B两点之间(含A、B两点)的图象记为M,当图象M的最高点与最低点的纵坐标之差为2时,求m的值.
14.在平面直角坐标系中,将函数(为常数)的图象记为,图象
的最低点为(,).
(1)当时,写出这个函数的表达式,并在所给坐标系中画出对应的图象.
(2)当时,求的值.
(3)求的最大值.
(4)当,且当图象与轴有两个交点时,设左边交点的横坐标为,直接写出的取值范围.
15.在平面直角坐标系中,函数(x≤2)的图象记为.
(1)图象过定点 .
(2)若图象的最高点到x轴的距离为1,求此时m的值.
(3)将图象沿直线x=2翻折,翻折后的图象记为,和合称为图象G.
①当m=0时,在如图的平面直角坐标系中画出图象G.
②点A(,)、B(,),当图象G和线段AB有且只有两
个公共点时,直接写出m的取值范围.
16.如图,在平面直角坐标系中,抛物线与x轴正半轴交于点A,过点A的直线与该抛物线的另一个交点B的横坐标为2.P是该抛物线上的任意一点,其横坐标为m+1,过点P作x轴的垂线,交直线AB于点C,在该垂线的点P上方取一点D,使PD=1,以CD为边作矩形CDEF.设点E的横坐标为2m.
(1)求直线AB对应的函数关系式.
(2)当点P与点A重合时,求点E的坐标.
(3)当点E在该抛物线上时,求抛物线的顶点到EF的距离.
(4)当矩形CDEF的一组邻边与该抛物线相交,且该抛物线在矩形CDEF内的部分所对应的函数值y随x的增大而增大时,直接写出m的取值范围.
二次函数单元练习一
1.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式.则下列说法中正确的是D
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
2.在平面直角坐标系中,二次函数y= ax2+bx+c(a≠0)的图象如图所示.则下列结论错误的是D
(A)ac<0. (B)b2-4ac>0. (C)4a+2b+c>0. (D)3b <2c.
3. 如图,在平面直角坐标系中,抛物线经过坐标原点O,与x轴的另一个交点为A.过抛物线的顶点B分别作BC⊥x轴于点C、BD⊥y轴于点D,则图中阴影部分图形的面积和为A
(A)18. (B)12. (C)9. (D)6.
4.如图,在平面直角坐标系中,正方形OABC的顶点A在x轴正半轴上,顶点C在y轴正半轴上,抛物线经过点B、C.若抛物线的顶点在正方形OABC的内部,则a的取值范围是 .
5.如图,在平面直角坐标系中,抛物线y=ax2-4ax+3(a<0)交y轴于点A,过点A作x轴的平行线交抛物线于点B,连结OB.点C是线段OB上一动点,以OA、AC为邻边作□OACD,则□OACD周长的最小值为________.
6.如图,在平面直角坐标系中,抛物线的顶点为A,在x轴下方作垂直于y轴的直线BC交该抛物线于点B、C,连结AB、AC.若点B到x轴的距离是点A到x轴的距离的3倍,则△ABC的面积为 .8
7.在平面直角坐标系中,抛物线的对称轴为直线x=1.若关于x的一元二次方程(t为实数)在-18.某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,该山区组织村民加工包装土特产销售给游客,以增加村民收入.已知某种土特产每袋成本10元,试销阶段每袋的销售价x(元)与该土特产的日销售量y(袋)之间的关系如下表:
x(元) 15 20 30 …
y(袋) 25 20 10 …
(1)若日销售量y(袋)是销售价x(元)的一次函数,求y与x之间的函数表达式.
(2)假设后续销售情况与试销阶段效果相同,设每日销售土特产的利润为w(元).
①求w与x之间的函数表达式.
②要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元 每日销售的最大利润是多少元
8.(1)设y与x之间的函数表达式为y=kx+b(k≠0),
根据题意,得解得
∴y与x之间的函数表达式为y=- x+40.
(2)①w=(x-10)(- x+40)=.
②w=.当x=25时,w取得最大值,最大值为w=225.
∴每袋的销售价应定为25元时,每日销售的利润最大是225元.
9.已知抛物线与x轴交于点A和B,第一象限内的点C在该抛物线上.
(1)直接写出A、B两点的坐标.
(2)若△ABC的面积为12,求点C坐标.
(3)在(2)问的条件下,直线经过点A、C.当>时,直接写出x的取值范围.
9.(1)A(-1,0) B(3,0)
(2)∵A(-1,0) B(3,0)∴AB=4
∵ ∴,
∴ ∴ (不符题意,舍去)∴ C(5,6)
(3)或 .
10.如图①,一个横截面为抛物线形的隧道,其底部的宽AB为8 m,拱高为4 m.该隧道为双向车道,且两车道之间有0.4 m的隔离带.一辆宽为2 m的货车要安全通过这条隧道,需保持其顶部与隧道有不少于0.5 m的空隙.按如图②所示建立平面直角坐标系.
(1)求该抛物线对应的函数关系式.
(2)通过计算说明该货车能够安全通行的最大高度.
10.(1)设抛物线解析式为y=ax2+k.
由题意,得解得∴抛物线表达式为.
(2)当时,y=2.79.当y=2.79时,2.79﹣0.5=2.29 m.
答:该货车能够通行的最大高度为2.29 m.
11.如图,隧道的横截面由抛物线形和矩形OABC构成.矩形一边OA的长是12m,另一边OC的长是1m.抛物线上的最高点D到地面OA的距离为7m.以OA所在直线为x轴,以OC所在直线为y轴,建立平面直角坐标系.
(1)求该抛物线所对应的函数表达式.
(2)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度为5m,求两排灯之间的水平距离.
(3)隧道内车辆双向通行,规定车辆必须在中心线两侧行驶,并保持车辆顶部与隧道有不少于m的空隙.现有一辆货运汽车,在隧道内距离道路边缘2m处行驶,求这辆货运汽车载物后的最大高度.
(第11题)
11.(1)由题意设抛物线所对应的函数表达式为.
将点C(0,1)代入上式,,解得.
∴该抛物线所对应的函数表达式为.(或)
(2)把y=5代入中,
,解得,.
.
所以两排灯之间的水平距离为m.
(3)把x=2代入中, .
.所以这辆货运汽车载物后的最大高度为4m.
12.某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合,如图所示,以水平方向为x轴,喷水池中心为原点建立平面直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
12.(1)设右侧抛物线的函数关系式为.
把代入,得. 解得.
所以函数表达式为.
(2)令.解得 (舍去).
所以王师傅要站在离水池中心7米内.
13.在平面直角坐标系中,抛物线经过点(6,7),其对称轴为直线x=2.
(1)求这条抛物线所对应的函数表达式.
(2)当时,求函数值y的取值范围.
(3)当时,函数值y先随x的增大而减小,后随x的增大而增大,且y的最大值为7,则k的取值范围是 .
(4)已知A、B两点均在抛物线上,点A的横坐标为m,点B的横坐标为m+2.将抛物线上A、B两点之间(含A、B两点)的图象记为M,当图象M的最高点与最低点的纵坐标之差为2时,求m的值.
13. (1)由题意,得 解得
∴抛物线所对应的函数表达式为.
(2)∵,对称轴为直线x=2,
∴当x=2时,.
当时,.
当时,.
∴当时,y的取值范围是.
(3)
(4)点A、B的坐标分别为、.
当时,,解得(不合题意,舍去).
当时,,
解得,(不合题意,舍去).
当时,,解得,(不合题意,舍去).
当时,,解得(不合题意,舍去).
综上,m的值为或.
14.在平面直角坐标系中,将函数(为常数)的图象记为,图象的最低点为(,).
(1)当时,写出这个函数的表达式,并在所给坐标系中画出对应的图象.
(2)当时,求的值.
(3)求的最大值.
(4)当,且当图象与轴有两个交点时,设左边交点的横坐标为,直接写出的取值范围.
14.(1)当时,这个函数的表达式为,
(2).∵时,∴.
∴,.
(3)∵,∴当m=2时,的最大值是4.
(4).
15.在平面直角坐标系中,函数(x≤2)的图象记为.
(1)图象过定点 .
(2)若图象的最高点到x轴的距离为1,求此时m的值.
(3)将图象沿直线x=2翻折,翻折后的图象记为,和合称为图象G.
①当m=0时,在如图的平面直角坐标系中画出图象G.
②点A(,)、B(,),当图象G和线段AB有且只有两
个公共点时,直接写出m的取值范围.
15.(1)
(2)当时,最高点为.
1°.解得(舍),.
2°. 解得.
当时,最高点为. .解得.
所以m的值为或或.
(3)① 如图.
②且或或.
16.如图,在平面直角坐标系中,抛物线与x轴正半轴交于点A,过点A的直线与该抛物线的另一个交点B的横坐标为2.P是该抛物线上的任意一点,其横坐标为m+1,过点P作x轴的垂线,交直线AB于点C,在该垂线的点P上方取一点D,使PD=1,以CD为边作矩形CDEF.设点E的横坐标为2m.
(1)求直线AB对应的函数关系式.
(2)当点P与点A重合时,求点E的坐标.
(3)当点E在该抛物线上时,求抛物线的顶点到EF的距离.
(4)当矩形CDEF的一组邻边与该抛物线相交,且该抛物线在矩形CDEF内的部分所对应的函数值y随x的增大而增大时,直接写出m的取值范围.
16.(1)当x=2时,. ∴点B的坐标为(2,)
当y=0时,.解得x1=-1,x2=3.
∵抛物线与x轴正半轴交于点A,∴点A的坐标为(3,0).
由题意,得解得∴直线AB对应的函数关系式为.
(2)如图①,当点P与点A重合时,m+1=3.解得m=2.∴2m=4.
∵点D的纵坐标为1.∴点E的坐标为(4,1).
(3)将配方,得.∴抛物线的顶点坐标为(1,-2).
由题意,得点E的坐标为.∵点E在该抛物线上,
∴.解得,.
如图②,当2m<1时,即,顶点(1,-2)在EF的右边.∵,
∴抛物线的顶点到EF的距离为.
如图③,当2m>1时,即,顶点(1,-2)在EF的左边. ∵,
∴抛物线的顶点到EF的距离为.
(4)当或或时,矩形CDEF的一组邻边与该抛物线相交.
也可以写成:当或或时,矩形CDEF的一组邻边与该抛物线相交.
【提示】如图④、图⑤、图⑥.
(第2题) (第3题) (第4题)
(第5题) (第6题)
x
O
A
B
C
y
(第9题)
图① 图②
(第10题)
(第12题)
-3
-2
-2
-1
1
1
2
2
3
3
-1
y
x
O
4
(第14题)
(第15题)
(第16题)
(第2题) (第3题) (第4题)
(第5题) (第6题)
x
O
A
B
C
y
(第9题)
图① 图②
(第10题)
(第12题)
-3
-2
-2
-1
1
1
2
2
3
3
-1
y
x
O
4
(第14题)
(第15题)
(第16题)
图①
图② 图③
图④ 图⑤ 图⑥
PAGE
1
1.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
2.在平面直角坐标系中,二次函数y= ax2+bx+c(a≠0)的图象如图所示.则下列结论错误的是( )
(A)ac<0. (B)b2-4ac>0. (C)4a+2b+c>0. (D)3b <2c.
3. 如图,在平面直角坐标系中,抛物线经过坐标原点O,与x轴的另一个交点为A.过抛物线的顶点B分别作BC⊥x轴于点C、BD⊥y轴于点D,则图中阴影部分图形的面积和为( )
(A)18. (B)12. (C)9. (D)6.
4.如图,在平面直角坐标系中,正方形OABC的顶点A在x轴正半轴上,顶点C在y轴正半轴上,抛物线经过点B、C.若抛物线的顶点在正方形OABC的内部,则a的取值范围是 .
5.如图,在平面直角坐标系中,抛物线y=ax2-4ax+3(a<0)交y轴于点A,过点A作x轴的平行线交抛物线于点B,连结OB.点C是线段OB上一动点,以OA、AC为邻边作□OACD,则□OACD周长的最小值为________.
6.如图,在平面直角坐标系中,抛物线的顶点为A,在x轴下方作垂直于y轴的直线BC交该抛物线于点B、C,连结AB、AC.若点B到x轴的距离是点A到x轴的距离的3倍,则△ABC的面积为 .
7.在平面直角坐标系中,抛物线的对称轴为直线x=1.若关于x的一元二次方程(t为实数)在-1
x(元) 15 20 30 …
y(袋) 25 20 10 …
(1)若日销售量y(袋)是销售价x(元)的一次函数,求y与x之间的函数表达式.
(2)假设后续销售情况与试销阶段效果相同,设每日销售土特产的利润为w(元).
①求w与x之间的函数表达式.
②要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元 每日销售的最大利润是多少元
9.已知抛物线与x轴交于点A和B,第一象限内的点C在该抛物线上.
(1)直接写出A、B两点的坐标.
(2)若△ABC的面积为12,求点C坐标.
(3)在(2)问的条件下,直线经过点A、C.当>时,直接写出x的取值范围.
10.如图①,一个横截面为抛物线形的隧道,其底部的宽AB为8 m,拱高为4 m.该隧道为双向车道,且两车道之间有0.4 m的隔离带.一辆宽为2 m的货车要安全通过这条隧道,需保持其顶部与隧道有不少于0.5 m的空隙.按如图②所示建立平面直角坐标系.
(1)求该抛物线对应的函数关系式.
(2)通过计算说明该货车能够安全通行的最大高度.
11.如图,隧道的横截面由抛物线形和矩形OABC构成.矩形一边OA的长是12m,另一边OC的长是1m.抛物线上的最高点D到地面OA的距离为7m.以OA所在直线为x轴,以OC所在直线为y轴,建立平面直角坐标系.
(1)求该抛物线所对应的函数表达式.
(2)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度为5m,求两排灯之间的水平距离.
(3)隧道内车辆双向通行,规定车辆必须在中心线两侧行驶,并保持车辆顶部与隧道有不少于m的空隙.现有一辆货运汽车,在隧道内距离道路边缘2m处行驶,求这辆货运汽车载物后的最大高度.
(第11题)
12.某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合,如图所示,以水平方向为x轴,喷水池中心为原点建立平面直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
13.在平面直角坐标系中,抛物线经过点(6,7),其对称轴为直线x=2.
(1)求这条抛物线所对应的函数表达式.
(2)当时,求函数值y的取值范围.
(3)当时,函数值y先随x的增大而减小,后随x的增大而增大,且y的最大值为7,则k的取值范围是 .
(4)已知A、B两点均在抛物线上,点A的横坐标为m,点B的横坐标为m+2.将抛物线上A、B两点之间(含A、B两点)的图象记为M,当图象M的最高点与最低点的纵坐标之差为2时,求m的值.
14.在平面直角坐标系中,将函数(为常数)的图象记为,图象
的最低点为(,).
(1)当时,写出这个函数的表达式,并在所给坐标系中画出对应的图象.
(2)当时,求的值.
(3)求的最大值.
(4)当,且当图象与轴有两个交点时,设左边交点的横坐标为,直接写出的取值范围.
15.在平面直角坐标系中,函数(x≤2)的图象记为.
(1)图象过定点 .
(2)若图象的最高点到x轴的距离为1,求此时m的值.
(3)将图象沿直线x=2翻折,翻折后的图象记为,和合称为图象G.
①当m=0时,在如图的平面直角坐标系中画出图象G.
②点A(,)、B(,),当图象G和线段AB有且只有两
个公共点时,直接写出m的取值范围.
16.如图,在平面直角坐标系中,抛物线与x轴正半轴交于点A,过点A的直线与该抛物线的另一个交点B的横坐标为2.P是该抛物线上的任意一点,其横坐标为m+1,过点P作x轴的垂线,交直线AB于点C,在该垂线的点P上方取一点D,使PD=1,以CD为边作矩形CDEF.设点E的横坐标为2m.
(1)求直线AB对应的函数关系式.
(2)当点P与点A重合时,求点E的坐标.
(3)当点E在该抛物线上时,求抛物线的顶点到EF的距离.
(4)当矩形CDEF的一组邻边与该抛物线相交,且该抛物线在矩形CDEF内的部分所对应的函数值y随x的增大而增大时,直接写出m的取值范围.
二次函数单元练习一
1.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式.则下列说法中正确的是D
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
2.在平面直角坐标系中,二次函数y= ax2+bx+c(a≠0)的图象如图所示.则下列结论错误的是D
(A)ac<0. (B)b2-4ac>0. (C)4a+2b+c>0. (D)3b <2c.
3. 如图,在平面直角坐标系中,抛物线经过坐标原点O,与x轴的另一个交点为A.过抛物线的顶点B分别作BC⊥x轴于点C、BD⊥y轴于点D,则图中阴影部分图形的面积和为A
(A)18. (B)12. (C)9. (D)6.
4.如图,在平面直角坐标系中,正方形OABC的顶点A在x轴正半轴上,顶点C在y轴正半轴上,抛物线经过点B、C.若抛物线的顶点在正方形OABC的内部,则a的取值范围是 .
5.如图,在平面直角坐标系中,抛物线y=ax2-4ax+3(a<0)交y轴于点A,过点A作x轴的平行线交抛物线于点B,连结OB.点C是线段OB上一动点,以OA、AC为邻边作□OACD,则□OACD周长的最小值为________.
6.如图,在平面直角坐标系中,抛物线的顶点为A,在x轴下方作垂直于y轴的直线BC交该抛物线于点B、C,连结AB、AC.若点B到x轴的距离是点A到x轴的距离的3倍,则△ABC的面积为 .8
7.在平面直角坐标系中,抛物线的对称轴为直线x=1.若关于x的一元二次方程(t为实数)在-1
x(元) 15 20 30 …
y(袋) 25 20 10 …
(1)若日销售量y(袋)是销售价x(元)的一次函数,求y与x之间的函数表达式.
(2)假设后续销售情况与试销阶段效果相同,设每日销售土特产的利润为w(元).
①求w与x之间的函数表达式.
②要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元 每日销售的最大利润是多少元
8.(1)设y与x之间的函数表达式为y=kx+b(k≠0),
根据题意,得解得
∴y与x之间的函数表达式为y=- x+40.
(2)①w=(x-10)(- x+40)=.
②w=.当x=25时,w取得最大值,最大值为w=225.
∴每袋的销售价应定为25元时,每日销售的利润最大是225元.
9.已知抛物线与x轴交于点A和B,第一象限内的点C在该抛物线上.
(1)直接写出A、B两点的坐标.
(2)若△ABC的面积为12,求点C坐标.
(3)在(2)问的条件下,直线经过点A、C.当>时,直接写出x的取值范围.
9.(1)A(-1,0) B(3,0)
(2)∵A(-1,0) B(3,0)∴AB=4
∵ ∴,
∴ ∴ (不符题意,舍去)∴ C(5,6)
(3)或 .
10.如图①,一个横截面为抛物线形的隧道,其底部的宽AB为8 m,拱高为4 m.该隧道为双向车道,且两车道之间有0.4 m的隔离带.一辆宽为2 m的货车要安全通过这条隧道,需保持其顶部与隧道有不少于0.5 m的空隙.按如图②所示建立平面直角坐标系.
(1)求该抛物线对应的函数关系式.
(2)通过计算说明该货车能够安全通行的最大高度.
10.(1)设抛物线解析式为y=ax2+k.
由题意,得解得∴抛物线表达式为.
(2)当时,y=2.79.当y=2.79时,2.79﹣0.5=2.29 m.
答:该货车能够通行的最大高度为2.29 m.
11.如图,隧道的横截面由抛物线形和矩形OABC构成.矩形一边OA的长是12m,另一边OC的长是1m.抛物线上的最高点D到地面OA的距离为7m.以OA所在直线为x轴,以OC所在直线为y轴,建立平面直角坐标系.
(1)求该抛物线所对应的函数表达式.
(2)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度为5m,求两排灯之间的水平距离.
(3)隧道内车辆双向通行,规定车辆必须在中心线两侧行驶,并保持车辆顶部与隧道有不少于m的空隙.现有一辆货运汽车,在隧道内距离道路边缘2m处行驶,求这辆货运汽车载物后的最大高度.
(第11题)
11.(1)由题意设抛物线所对应的函数表达式为.
将点C(0,1)代入上式,,解得.
∴该抛物线所对应的函数表达式为.(或)
(2)把y=5代入中,
,解得,.
.
所以两排灯之间的水平距离为m.
(3)把x=2代入中, .
.所以这辆货运汽车载物后的最大高度为4m.
12.某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合,如图所示,以水平方向为x轴,喷水池中心为原点建立平面直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
12.(1)设右侧抛物线的函数关系式为.
把代入,得. 解得.
所以函数表达式为.
(2)令.解得 (舍去).
所以王师傅要站在离水池中心7米内.
13.在平面直角坐标系中,抛物线经过点(6,7),其对称轴为直线x=2.
(1)求这条抛物线所对应的函数表达式.
(2)当时,求函数值y的取值范围.
(3)当时,函数值y先随x的增大而减小,后随x的增大而增大,且y的最大值为7,则k的取值范围是 .
(4)已知A、B两点均在抛物线上,点A的横坐标为m,点B的横坐标为m+2.将抛物线上A、B两点之间(含A、B两点)的图象记为M,当图象M的最高点与最低点的纵坐标之差为2时,求m的值.
13. (1)由题意,得 解得
∴抛物线所对应的函数表达式为.
(2)∵,对称轴为直线x=2,
∴当x=2时,.
当时,.
当时,.
∴当时,y的取值范围是.
(3)
(4)点A、B的坐标分别为、.
当时,,解得(不合题意,舍去).
当时,,
解得,(不合题意,舍去).
当时,,解得,(不合题意,舍去).
当时,,解得(不合题意,舍去).
综上,m的值为或.
14.在平面直角坐标系中,将函数(为常数)的图象记为,图象的最低点为(,).
(1)当时,写出这个函数的表达式,并在所给坐标系中画出对应的图象.
(2)当时,求的值.
(3)求的最大值.
(4)当,且当图象与轴有两个交点时,设左边交点的横坐标为,直接写出的取值范围.
14.(1)当时,这个函数的表达式为,
(2).∵时,∴.
∴,.
(3)∵,∴当m=2时,的最大值是4.
(4).
15.在平面直角坐标系中,函数(x≤2)的图象记为.
(1)图象过定点 .
(2)若图象的最高点到x轴的距离为1,求此时m的值.
(3)将图象沿直线x=2翻折,翻折后的图象记为,和合称为图象G.
①当m=0时,在如图的平面直角坐标系中画出图象G.
②点A(,)、B(,),当图象G和线段AB有且只有两
个公共点时,直接写出m的取值范围.
15.(1)
(2)当时,最高点为.
1°.解得(舍),.
2°. 解得.
当时,最高点为. .解得.
所以m的值为或或.
(3)① 如图.
②且或或.
16.如图,在平面直角坐标系中,抛物线与x轴正半轴交于点A,过点A的直线与该抛物线的另一个交点B的横坐标为2.P是该抛物线上的任意一点,其横坐标为m+1,过点P作x轴的垂线,交直线AB于点C,在该垂线的点P上方取一点D,使PD=1,以CD为边作矩形CDEF.设点E的横坐标为2m.
(1)求直线AB对应的函数关系式.
(2)当点P与点A重合时,求点E的坐标.
(3)当点E在该抛物线上时,求抛物线的顶点到EF的距离.
(4)当矩形CDEF的一组邻边与该抛物线相交,且该抛物线在矩形CDEF内的部分所对应的函数值y随x的增大而增大时,直接写出m的取值范围.
16.(1)当x=2时,. ∴点B的坐标为(2,)
当y=0时,.解得x1=-1,x2=3.
∵抛物线与x轴正半轴交于点A,∴点A的坐标为(3,0).
由题意,得解得∴直线AB对应的函数关系式为.
(2)如图①,当点P与点A重合时,m+1=3.解得m=2.∴2m=4.
∵点D的纵坐标为1.∴点E的坐标为(4,1).
(3)将配方,得.∴抛物线的顶点坐标为(1,-2).
由题意,得点E的坐标为.∵点E在该抛物线上,
∴.解得,.
如图②,当2m<1时,即,顶点(1,-2)在EF的右边.∵,
∴抛物线的顶点到EF的距离为.
如图③,当2m>1时,即,顶点(1,-2)在EF的左边. ∵,
∴抛物线的顶点到EF的距离为.
(4)当或或时,矩形CDEF的一组邻边与该抛物线相交.
也可以写成:当或或时,矩形CDEF的一组邻边与该抛物线相交.
【提示】如图④、图⑤、图⑥.
(第2题) (第3题) (第4题)
(第5题) (第6题)
x
O
A
B
C
y
(第9题)
图① 图②
(第10题)
(第12题)
-3
-2
-2
-1
1
1
2
2
3
3
-1
y
x
O
4
(第14题)
(第15题)
(第16题)
(第2题) (第3题) (第4题)
(第5题) (第6题)
x
O
A
B
C
y
(第9题)
图① 图②
(第10题)
(第12题)
-3
-2
-2
-1
1
1
2
2
3
3
-1
y
x
O
4
(第14题)
(第15题)
(第16题)
图①
图② 图③
图④ 图⑤ 图⑥
PAGE
1
