五年级下册数学课件-4.9表面积的变化 沪教版(共22张PPT)
文档属性
| 名称 | 五年级下册数学课件-4.9表面积的变化 沪教版(共22张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 08:10:00 | ||
图片预览





文档简介
(共22张PPT)
1cm
1cm
1cm
1cm
1cm
1cm
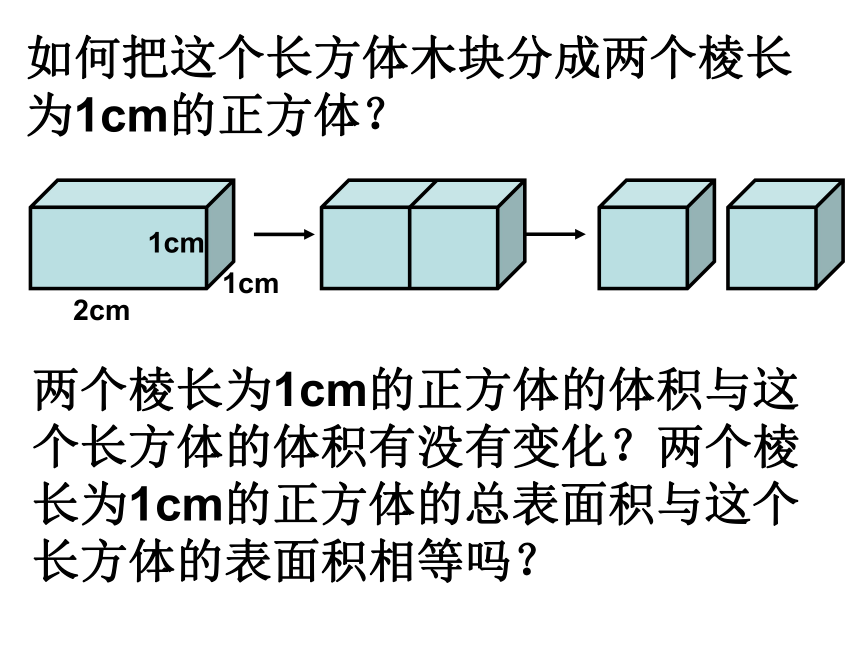
体积
V=a3
=1×1×1
=1(cm3)
表面积
S=6a2
=6×(1×1)
=6(cm2)
棱长是1cm的正方体,体积是多少?表面积是多少?
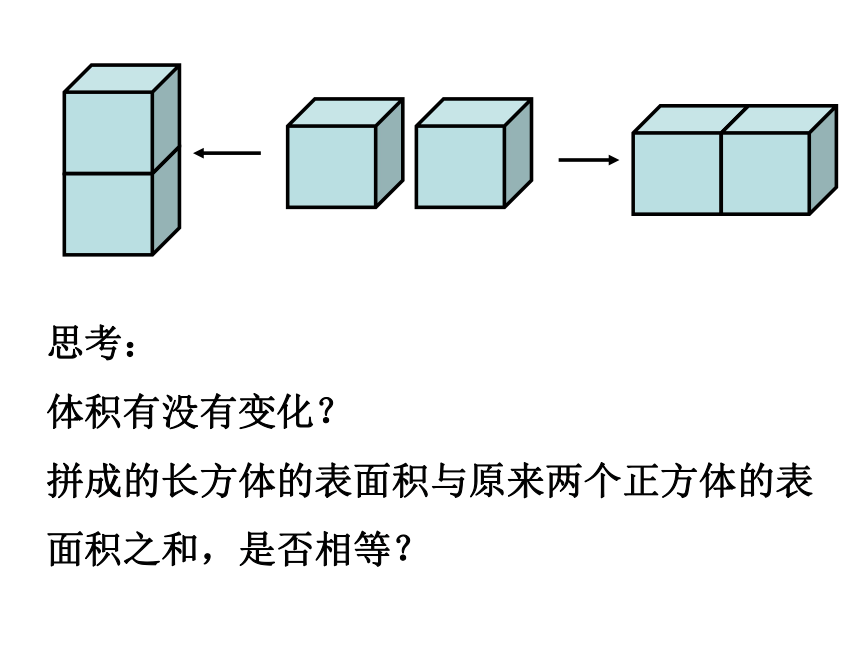
如何把这个长方体木块分成两个棱长为1cm的正方体?
两个棱长为1cm的正方体的体积与这个长方体的体积有没有变化?两个棱长为1cm的正方体的总表面积与这个长方体的表面积相等吗?
2cm
1cm
1cm
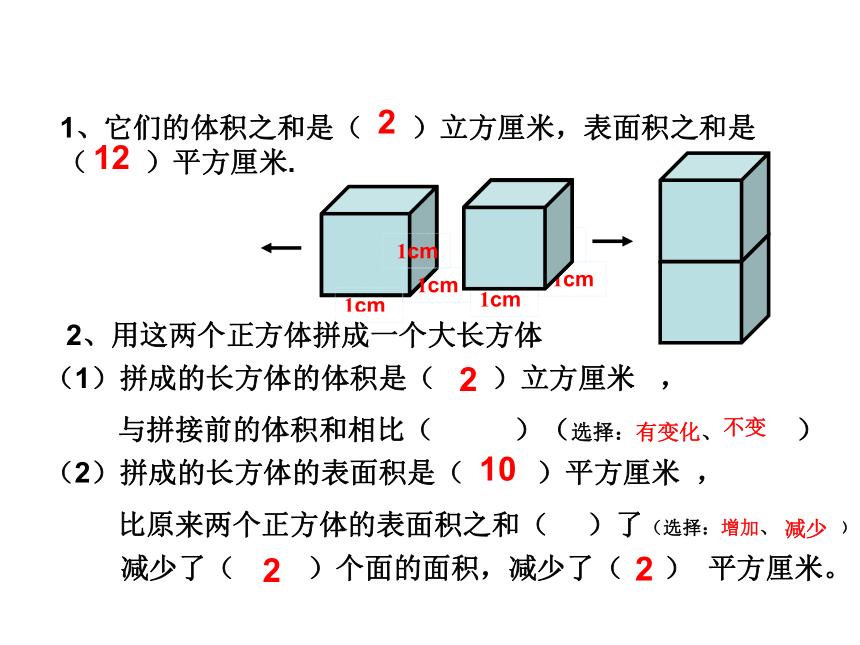
思考:
体积有没有变化?
拼成的长方体的表面积与原来两个正方体的表
面积之和,是否相等?
每重叠一次减少二个面。
1、它们的体积之和是( )立方厘米,表面积之和是 ( )平方厘米.
1cm
1cm
1cm
1cm
1cm
1cm
2、用这两个正方体拼成一个大长方体
(1)拼成的长方体的体积是( )立方厘米 ,
与拼接前的体积和相比( )(选择:有变化、不变 )
(2)拼成的长方体的表面积是( )平方厘米 ,
比原来两个正方体的表面积之和( )了(选择:增加、 减少 )
减少了( )个面的面积,减少了( ) 平方厘米。
2
12
2
10
减少
2
2
不变
如果用3个、4个、5个或更多个1立方厘米的正方体排成一行,拼成长方体,它们的表面积又有什么变化呢?
正方体的个数 2 3 4 5 ……
原来正方体的表面积之和(cm2) ……
拼接次数 ……
拼成长方体后减少了原来几个面的面积 ……
拼成的长方体的表面积( cm2) ……
……
12
1
2
10
18
2
4
14
24
3
6
18
30
4
8
22
原来正方体的表面积之和 - 拼成长方
体后减少的正方形面的面积 = 拼成的
长方体的表面积。
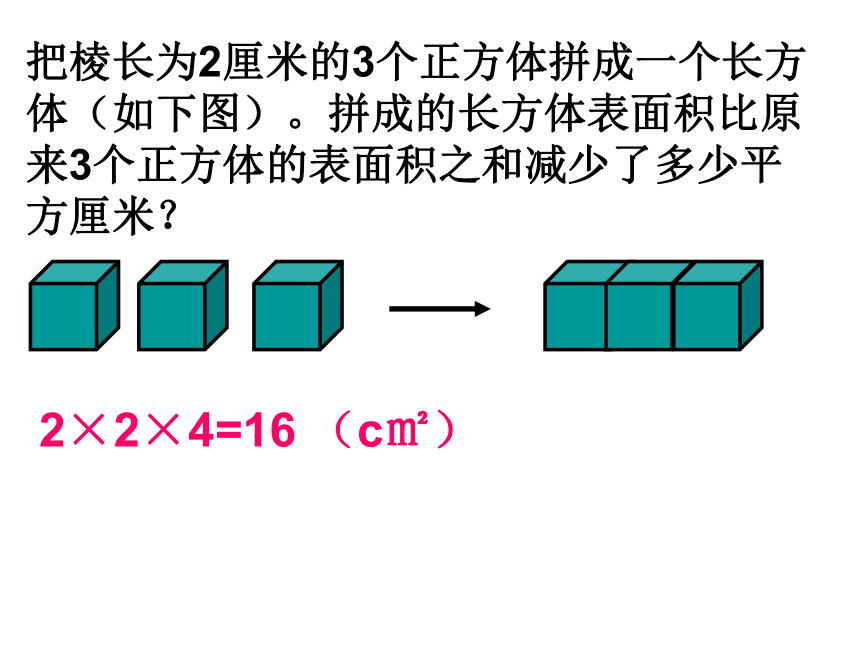
把棱长为2厘米的3个正方体拼成一个长方体(如下图)。拼成的长方体表面积比原来3个正方体的表面积之和减少了多少平方厘米?
2×2×4=16 (c㎡)
重叠面越多,表面积减少越多。
2cm
1cm
1cm
切成的长方体个数 2 3 4 5 …
切割次数 …
增加了几个面 …
1
2
2
4
3
6
4
8
每切割一次增加二个面。
把一个长为6分米的长方体切成两个大小相等的正方体,这2个正方体的表面积的总和比原来长方体的表面积增加了多少平方分米?
6dm
3dm
3dm
把一个长为6分米的长方体切成两个大小相等的正方体,这2个正方体的表面积的总和比原来长方体的表面积增加了多少平方分米?
3dm
3dm
3dm
把一个长为6分米的长方体切成两个大小相等的正方体,这2个正方体的表面积的总和比原来长方体的表面积增加了多少平方分米?
3dm
3dm
3dm
3×3×2=18(c㎡)
①用两个棱长是1厘米的小正方体拼成一个长方体,
( )没有变化,( )有变化;
②用5个棱长是1厘米的小正方体拼成一个长方体,
表面积减少( )个面的面积;
③把三个棱长都是5厘米的正方体拼成一个长方体,
这个长方体的表面积是( )平方厘米;
A、350 B、450 C、550
④判断:把3个棱长1厘米的正方体拼成一个长方体,
长方体的表面积是18平方厘米。( )
体积
表面积
8
A
×
练习
一根长方体木料,长2米,宽和高都是0.1米。
两个小长方体的表面积之和比原来长方体的表面积( )(选择:增加了、减少了),
增加了( )平方米。
①如果把它锯成两个相等的小长方体,
增加了
0.02
一根长方体木料,长2米,宽和高都是0.1米。
②如果把它锯成三个不相等的长方体,
三个小长方体的表面积之和比原来长方体的表面积增加了( )平方米.
0.04
解法二:
用8个棱长是1厘米的小正方体拼成一个大的长方体(或正方体)。拼成的这个长方体(或正方体)的表面积最大是多少平方厘米 最小是多少平方厘米?
最大:
解法一:
1×1×6×8- 1×1×2×7
=48- 14
=34(平方厘米)
8×1×4+1×1×2
=32+2
=34(平方厘米)
解法二:
解法一:
用8个棱长是1厘米的小正方体拼成一个大的长方体(或正方体)。拼成的这个长方体(或正方体)的表面积最大是多少平方厘米 最小是多少平方厘米?
1×1×3×8
=24(平方厘米)
2×2×6
=24(平方厘米)
最小:
1cm
1cm
1cm
1cm
1cm
1cm
用两个棱长为1cm的正方体拼成一个长方体后表面积有什么变化?
1cm
1cm
1cm
1cm
1cm
1cm
体积
V=a3
=1×1×1
=1(cm3)
表面积
S=6a2
=6×(1×1)
=6(cm2)
棱长是1cm的正方体,体积是多少?表面积是多少?
如何把这个长方体木块分成两个棱长为1cm的正方体?
两个棱长为1cm的正方体的体积与这个长方体的体积有没有变化?两个棱长为1cm的正方体的总表面积与这个长方体的表面积相等吗?
2cm
1cm
1cm
思考:
体积有没有变化?
拼成的长方体的表面积与原来两个正方体的表
面积之和,是否相等?
每重叠一次减少二个面。
1、它们的体积之和是( )立方厘米,表面积之和是 ( )平方厘米.
1cm
1cm
1cm
1cm
1cm
1cm
2、用这两个正方体拼成一个大长方体
(1)拼成的长方体的体积是( )立方厘米 ,
与拼接前的体积和相比( )(选择:有变化、不变 )
(2)拼成的长方体的表面积是( )平方厘米 ,
比原来两个正方体的表面积之和( )了(选择:增加、 减少 )
减少了( )个面的面积,减少了( ) 平方厘米。
2
12
2
10
减少
2
2
不变
如果用3个、4个、5个或更多个1立方厘米的正方体排成一行,拼成长方体,它们的表面积又有什么变化呢?
正方体的个数 2 3 4 5 ……
原来正方体的表面积之和(cm2) ……
拼接次数 ……
拼成长方体后减少了原来几个面的面积 ……
拼成的长方体的表面积( cm2) ……
……
12
1
2
10
18
2
4
14
24
3
6
18
30
4
8
22
原来正方体的表面积之和 - 拼成长方
体后减少的正方形面的面积 = 拼成的
长方体的表面积。
把棱长为2厘米的3个正方体拼成一个长方体(如下图)。拼成的长方体表面积比原来3个正方体的表面积之和减少了多少平方厘米?
2×2×4=16 (c㎡)
重叠面越多,表面积减少越多。
2cm
1cm
1cm
切成的长方体个数 2 3 4 5 …
切割次数 …
增加了几个面 …
1
2
2
4
3
6
4
8
每切割一次增加二个面。
把一个长为6分米的长方体切成两个大小相等的正方体,这2个正方体的表面积的总和比原来长方体的表面积增加了多少平方分米?
6dm
3dm
3dm
把一个长为6分米的长方体切成两个大小相等的正方体,这2个正方体的表面积的总和比原来长方体的表面积增加了多少平方分米?
3dm
3dm
3dm
把一个长为6分米的长方体切成两个大小相等的正方体,这2个正方体的表面积的总和比原来长方体的表面积增加了多少平方分米?
3dm
3dm
3dm
3×3×2=18(c㎡)
①用两个棱长是1厘米的小正方体拼成一个长方体,
( )没有变化,( )有变化;
②用5个棱长是1厘米的小正方体拼成一个长方体,
表面积减少( )个面的面积;
③把三个棱长都是5厘米的正方体拼成一个长方体,
这个长方体的表面积是( )平方厘米;
A、350 B、450 C、550
④判断:把3个棱长1厘米的正方体拼成一个长方体,
长方体的表面积是18平方厘米。( )
体积
表面积
8
A
×
练习
一根长方体木料,长2米,宽和高都是0.1米。
两个小长方体的表面积之和比原来长方体的表面积( )(选择:增加了、减少了),
增加了( )平方米。
①如果把它锯成两个相等的小长方体,
增加了
0.02
一根长方体木料,长2米,宽和高都是0.1米。
②如果把它锯成三个不相等的长方体,
三个小长方体的表面积之和比原来长方体的表面积增加了( )平方米.
0.04
解法二:
用8个棱长是1厘米的小正方体拼成一个大的长方体(或正方体)。拼成的这个长方体(或正方体)的表面积最大是多少平方厘米 最小是多少平方厘米?
最大:
解法一:
1×1×6×8- 1×1×2×7
=48- 14
=34(平方厘米)
8×1×4+1×1×2
=32+2
=34(平方厘米)
解法二:
解法一:
用8个棱长是1厘米的小正方体拼成一个大的长方体(或正方体)。拼成的这个长方体(或正方体)的表面积最大是多少平方厘米 最小是多少平方厘米?
1×1×3×8
=24(平方厘米)
2×2×6
=24(平方厘米)
最小:
1cm
1cm
1cm
1cm
1cm
1cm
用两个棱长为1cm的正方体拼成一个长方体后表面积有什么变化?
