五年级下册数学课件-4.9表面积的变化 沪教版(共27张PPT)
文档属性
| 名称 | 五年级下册数学课件-4.9表面积的变化 沪教版(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 08:11:48 | ||
图片预览





文档简介
(共27张PPT)
表面积的变化
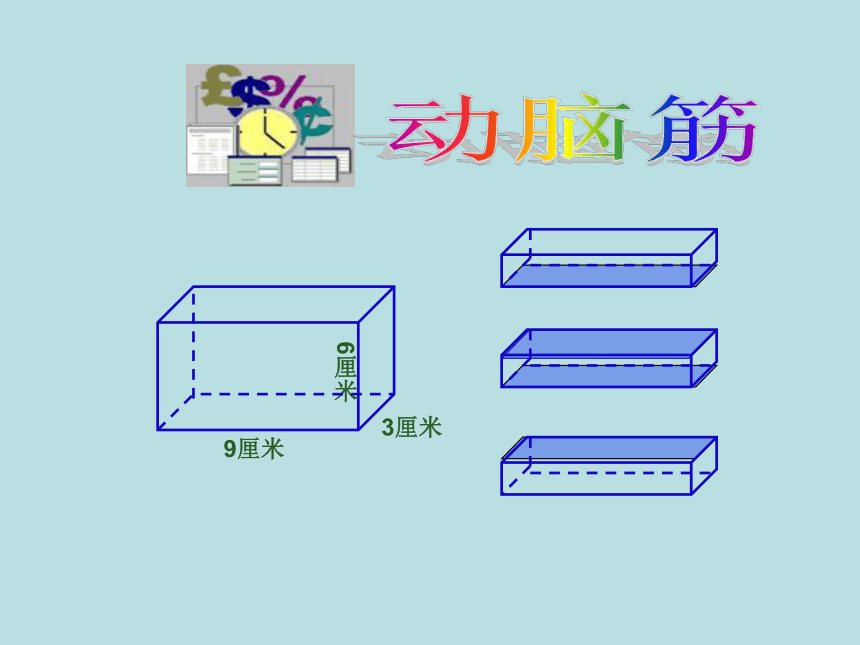
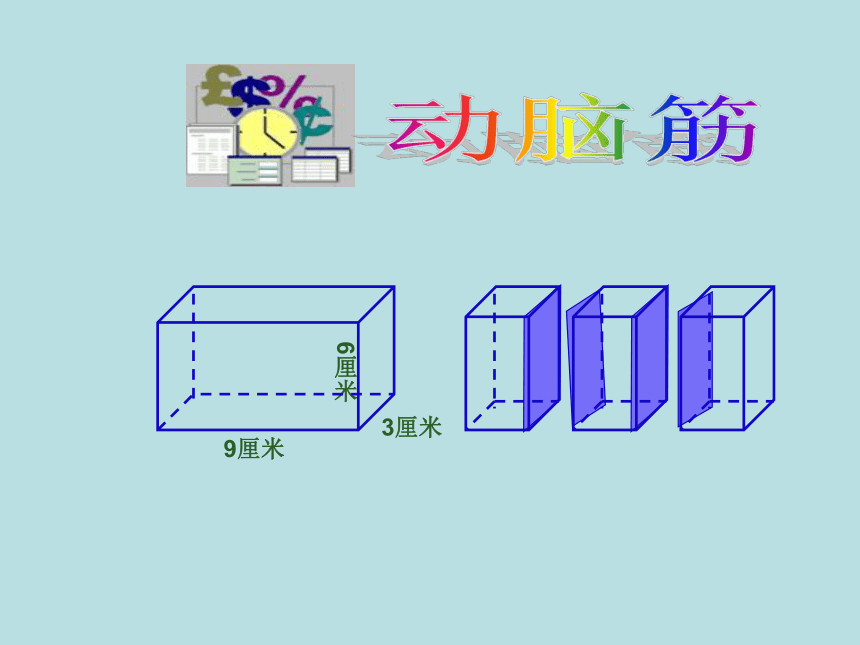
(如图)把这个长方体平均分成三个相等的小长方体,表面积增加了多少平方厘米?
3厘米
9厘米
6厘米
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
4
4
8
表面积比原来( )了 ( )平方厘米。
增加
32
4×4×2=32平方厘米
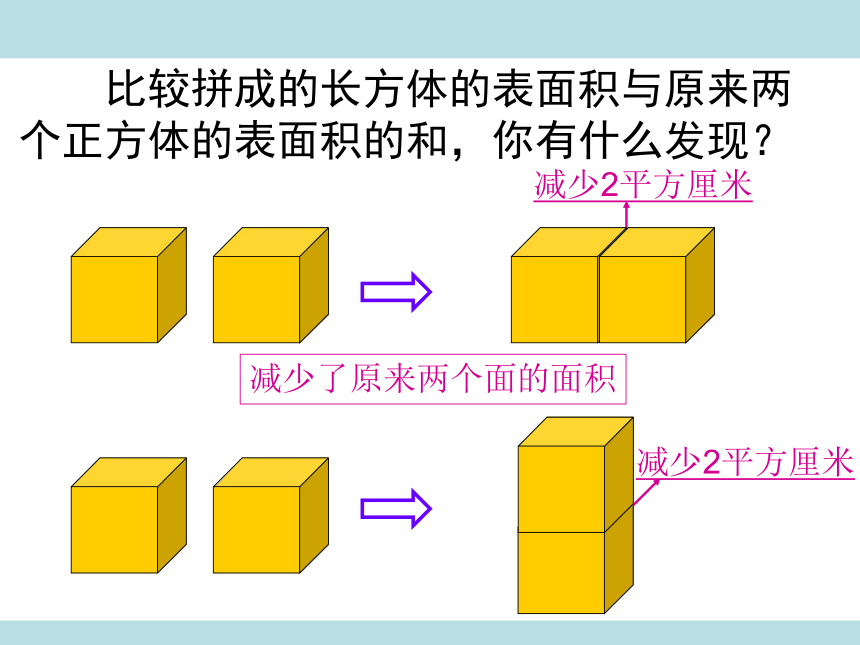
比较拼成的长方体的表面积与原来两个正方体的表面积的和,你有什么发现?
减少2平方厘米
减少2平方厘米
减少了原来两个面的面积
用3个这样的正方体拼成一个长方体,表面积比原来减少几个正方形面的面积?
减少2个面
减少2个面
用4个这样的正方体拼成一个长方体,表面积比原来减少几个正方形面的面积?
减少2个面
减少2个面
减少2个面
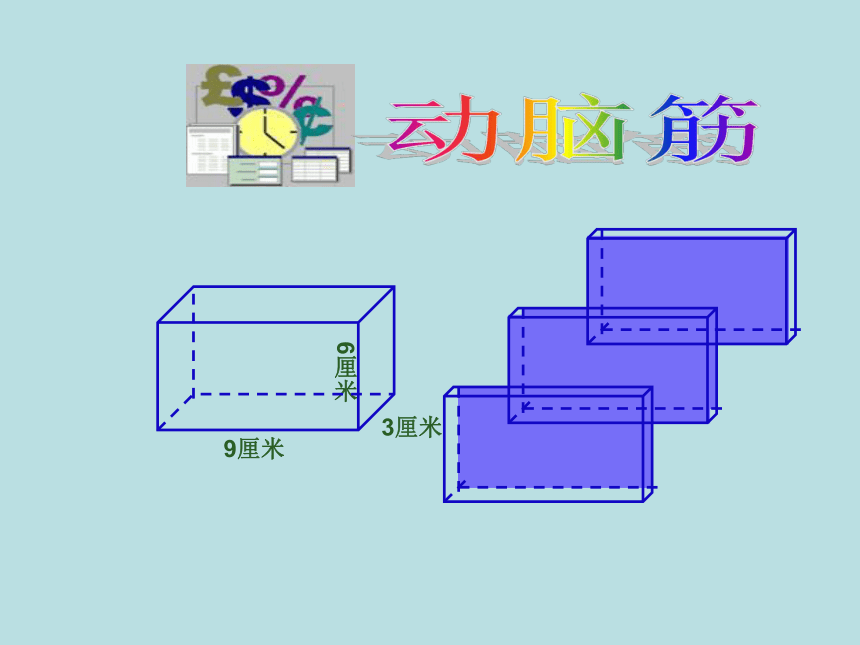
用下面的两个长方体拼成三个不同的大长方体,你有什么发现?
5cm
4cm
3cm
5cm
4cm
3cm
用下面的两个长方体拼成三个不同的大长方体,你有什么发现?
5cm
4cm
3cm
5cm
4cm
3cm
用下面的两个长方体拼成三个不同的大长方体,你有什么发现?
5cm
4cm
3cm
5cm
4cm
3cm
用下面的两个长方体拼成三个不同的大长方体,你有什么发现?
5cm
4cm
3cm
5cm
4cm
3cm
都减少了原来两个面的面积
5×4×2
5×3×2
3×4×2
表面积最小
1、把两个棱长为1厘米的正方体拼成一个长方体,表面积减少多少平方厘米?
下面各题先画图,再解答:
1×1×2=2(平方厘米)
答:表面积减少2平方厘米。
2、把三个棱长为1厘米的正方体拼成一个长方体,表面积减少多少平方厘米?
1×1×4=4(平方厘米)
答:表面积减少4平方厘米。
3、把四个棱长为1厘米的正方体拼成一个长方体,表面积减少多少平方厘米?你能想出几种拼法?
1×1×6=6(平方厘米)
答:表面积减少6平方厘米。
1×1×8=8(平方厘米)
答:表面积减少8平方厘米。
4、把八个棱长为1厘米的正方体拼成一个大正方体,表面积减少多少平方厘米?
有其他的解法吗?
1×1×8×3=24(平方厘米)
1×1×6×8=48(平方厘米)
2×2×6=24(平方厘米)
48-24=24(平方厘米)
答:表面积减少24平方厘米。
5、如图,把一个长为6分米,宽和高均为3分米的长方体切成两个正方体,表面积将会发生怎样的变化?
6、把一个横截面边长为1分米,长为5分米的长方体切3刀,表面积将会增加多少平方分米?
5、把两个长为3分米,宽为2分米,高为1分米的长方体拼成一个长方体,表面积最少减少多少平方分米?最多减少多少平方分米?
表面积最大是多少平方分米?最少是多少平方分米?
(2)棱长之和是24厘米的正方体,它的表面积是多少平方厘米.( )
A.36 B.24 C.18
(3)一个棱长的总和是60厘米的正方体,求它的表面积算式是 ( )
A.(60÷8)×(60÷8)×60
B.(60÷4)×(60÷4)×6
C.(60÷12)×(60÷12)×6
D.60×60×60
(1)做一个不带盖的长方体铁盒,长5分米,宽3分米,高1分米,至少需要多少平方分米的铁皮? ( )
A.5×1+(5×3+1×3)×2=41(平方分米)
B.1×3+(5×1+5×3)×2=43(平方分米)
C.5×3+(5×1+3×1)×2=31(平方分米)
C
B
C
(4)把一个棱长5厘米的正方体,分割成两个长方体,再在表面涂上漆,这两个长方体涂漆的总面积是多少平方厘米。 ( )
A.125 B.150 C.175 D.200
D
3、选择题。
选择题:
5、如果长方体的长、宽、高都扩大3倍,那么它的表面积扩大( )倍。
A、3 B、6 C、9
6、把两个正方体拼成一个长方体,它的表面积减少了( )面的面积。
A、1 B、2 C、3
B
C
下图表示用棱长1厘米的正方体摆成的物体。
(1)从上面、正面和左侧面看到的分别是什么形状?试着画一画。
上面
正面
左侧
(2)这个物体的表面积是多少平方厘米?
(3)在这个物体上添加同样大的正方体,补成一个大正方体。这个大正方体的表面积至少是多少平方厘米?
8
12
6
1
有一个长方体纸盒,量得它的长、
宽、高分别是16厘米、8厘米、12厘
米。
1、做这个纸盒至少用了多少平方
厘米纸板?
2、如果盒子不带盖,怎样计算它的
纸板用料。
3、如果在它的四周贴上一层商标
纸,怎样计算商标纸的面积?
一个长方体教室长8米,宽7米,高4米。教室的门窗和黑板的面积一共有35平方米。要粉刷教室的顶面和四面墙壁,粉刷的面积有多少平方米?
如果每平方米需工料费1.5元,
粉刷工料共需多少元?
一节通风管长50厘米,宽10厘米,高8厘米,做这样的一对通风管至少需要多少铁皮?
50
10
8
表面积的变化
(如图)把这个长方体平均分成三个相等的小长方体,表面积增加了多少平方厘米?
3厘米
9厘米
6厘米
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
4
4
8
表面积比原来( )了 ( )平方厘米。
增加
32
4×4×2=32平方厘米
比较拼成的长方体的表面积与原来两个正方体的表面积的和,你有什么发现?
减少2平方厘米
减少2平方厘米
减少了原来两个面的面积
用3个这样的正方体拼成一个长方体,表面积比原来减少几个正方形面的面积?
减少2个面
减少2个面
用4个这样的正方体拼成一个长方体,表面积比原来减少几个正方形面的面积?
减少2个面
减少2个面
减少2个面
用下面的两个长方体拼成三个不同的大长方体,你有什么发现?
5cm
4cm
3cm
5cm
4cm
3cm
用下面的两个长方体拼成三个不同的大长方体,你有什么发现?
5cm
4cm
3cm
5cm
4cm
3cm
用下面的两个长方体拼成三个不同的大长方体,你有什么发现?
5cm
4cm
3cm
5cm
4cm
3cm
用下面的两个长方体拼成三个不同的大长方体,你有什么发现?
5cm
4cm
3cm
5cm
4cm
3cm
都减少了原来两个面的面积
5×4×2
5×3×2
3×4×2
表面积最小
1、把两个棱长为1厘米的正方体拼成一个长方体,表面积减少多少平方厘米?
下面各题先画图,再解答:
1×1×2=2(平方厘米)
答:表面积减少2平方厘米。
2、把三个棱长为1厘米的正方体拼成一个长方体,表面积减少多少平方厘米?
1×1×4=4(平方厘米)
答:表面积减少4平方厘米。
3、把四个棱长为1厘米的正方体拼成一个长方体,表面积减少多少平方厘米?你能想出几种拼法?
1×1×6=6(平方厘米)
答:表面积减少6平方厘米。
1×1×8=8(平方厘米)
答:表面积减少8平方厘米。
4、把八个棱长为1厘米的正方体拼成一个大正方体,表面积减少多少平方厘米?
有其他的解法吗?
1×1×8×3=24(平方厘米)
1×1×6×8=48(平方厘米)
2×2×6=24(平方厘米)
48-24=24(平方厘米)
答:表面积减少24平方厘米。
5、如图,把一个长为6分米,宽和高均为3分米的长方体切成两个正方体,表面积将会发生怎样的变化?
6、把一个横截面边长为1分米,长为5分米的长方体切3刀,表面积将会增加多少平方分米?
5、把两个长为3分米,宽为2分米,高为1分米的长方体拼成一个长方体,表面积最少减少多少平方分米?最多减少多少平方分米?
表面积最大是多少平方分米?最少是多少平方分米?
(2)棱长之和是24厘米的正方体,它的表面积是多少平方厘米.( )
A.36 B.24 C.18
(3)一个棱长的总和是60厘米的正方体,求它的表面积算式是 ( )
A.(60÷8)×(60÷8)×60
B.(60÷4)×(60÷4)×6
C.(60÷12)×(60÷12)×6
D.60×60×60
(1)做一个不带盖的长方体铁盒,长5分米,宽3分米,高1分米,至少需要多少平方分米的铁皮? ( )
A.5×1+(5×3+1×3)×2=41(平方分米)
B.1×3+(5×1+5×3)×2=43(平方分米)
C.5×3+(5×1+3×1)×2=31(平方分米)
C
B
C
(4)把一个棱长5厘米的正方体,分割成两个长方体,再在表面涂上漆,这两个长方体涂漆的总面积是多少平方厘米。 ( )
A.125 B.150 C.175 D.200
D
3、选择题。
选择题:
5、如果长方体的长、宽、高都扩大3倍,那么它的表面积扩大( )倍。
A、3 B、6 C、9
6、把两个正方体拼成一个长方体,它的表面积减少了( )面的面积。
A、1 B、2 C、3
B
C
下图表示用棱长1厘米的正方体摆成的物体。
(1)从上面、正面和左侧面看到的分别是什么形状?试着画一画。
上面
正面
左侧
(2)这个物体的表面积是多少平方厘米?
(3)在这个物体上添加同样大的正方体,补成一个大正方体。这个大正方体的表面积至少是多少平方厘米?
8
12
6
1
有一个长方体纸盒,量得它的长、
宽、高分别是16厘米、8厘米、12厘
米。
1、做这个纸盒至少用了多少平方
厘米纸板?
2、如果盒子不带盖,怎样计算它的
纸板用料。
3、如果在它的四周贴上一层商标
纸,怎样计算商标纸的面积?
一个长方体教室长8米,宽7米,高4米。教室的门窗和黑板的面积一共有35平方米。要粉刷教室的顶面和四面墙壁,粉刷的面积有多少平方米?
如果每平方米需工料费1.5元,
粉刷工料共需多少元?
一节通风管长50厘米,宽10厘米,高8厘米,做这样的一对通风管至少需要多少铁皮?
50
10
8
