华师大版九年级数学下册试题 26.1二次函数 一课一练习题1(word版含答案)
文档属性
| 名称 | 华师大版九年级数学下册试题 26.1二次函数 一课一练习题1(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 139.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 09:46:00 | ||
图片预览


文档简介
26.1《二次函数》习题1
第一课时
1.写出下列二次函数的二次项系数,一次项系数和常数项.
(1)在 中 , , ;
(2) 在中 , , ;
(3)在中 , , ;
2. 已知是关于的二次函数,则 。
3.三角形一边长为,这边上的高比的2倍少1,,则三角形的面积与之间的关系为 。
4.某厂2004年创利320万元, 如果以后每年以相同的增长率x递增, 2005年和2006年两年共创利万元,则关于的函数关系式是: .(用y=ax2+bx+c的形式表示)
5.下列函数:,,,,y=,,,其中是二次函数的有( )
A.1个 B. 2个 C. 3个 D. 4个
6.用20米长的篱笆围成一个长方形的院子,如果这个院子的面积是S米2,院子的一边长为,那么,S与的函数关系式为( )
A. B.
C. D.
7.已知:函数是二次函数,求的值并写出此函数的解析式.
8.在新年到来之际,班里每个同学都为其它同学制做了一张贺年卡,若这个班里有个同学,那么请你写出总共制作的贺年卡的张数与的函数解析式.
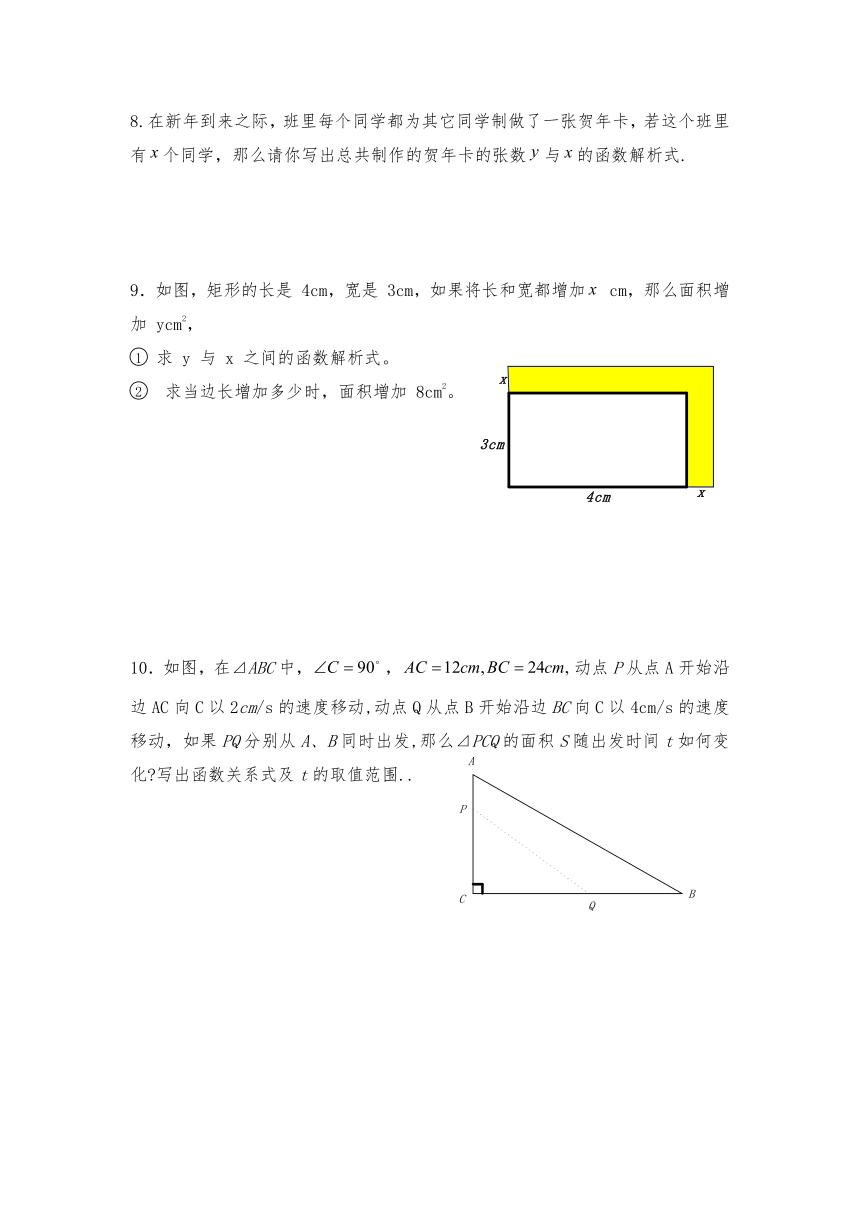
9.如图,矩形的长是 4cm,宽是 3cm,如果将长和宽都增加 cm,那么面积增加 ycm2,
求 y 与 x 之间的函数解析式。
求当边长增加多少时,面积增加 8cm2。
10.如图,在⊿ABC中,,动点P从点A开始沿边AC向C以2cm/s的速度移动,动点Q从点B开始沿边BC向C以4cm/s的速度移动,如果PQ分别从A、B同时出发,那么⊿PCQ的面积S随出发时间t如何变化 写出函数关系式及t的取值范围..
第二课时
一、 选择题
1.下列函数,是的二次函数的是( )
A. B. C. D.
2.函数是常数)是二次函数的条件的是( )
A. B.<0,
C.>0, D.
3. 下列函数不属二次函数的是( )
A.y=(x-1)(x+2) B.y=(x+1)2
C.y=2(x+3)2-2x2 D.y=1-x2
4.某工厂从国外进口了一套机器设备,现价值为50万元,但该套设备每年的折旧率为,那么两年之后这台机器的价值为万元,则与之间的函数关系式可以写为( )
A. B. C. D.
5.从半径是4cm的圆中挖去一个半径是xcm的圆面,剩下一个圆环的面积是ycm2,则y与x的函数关系是( )
A. B. C. D.
6.如图所示,直角三角形AOB中,AB⊥OB,且AB=OB=3,设直线,截此三角形所得的阴影部分面积是S,则S与t之间的函数关系是 ( )
A. B. C. D.
二、填空题
7.矩形的周长为80,设它们的一边长为,那么矩形的面积S与边长X之间的函数关系式为 .
8.若函数y=(k2-4)x2+(k+2)x+3是二次函数,则k______.
9.二次函数y=ax2+bx+c(a≠0)中,当b=0,c≠0时,函数表达式为______;
当b≠0, c=0时,函数表达式为______;当b=c=0时,函数表达式为______.
10.小李存入银行人民币500元,年利率为x%,两年到期,本息和为y元(不考虑利息税),y与x之间的函数关系是_______,若年利率为6%,两年到期的本利共______元.
11.如果函数是二次函数,则k得值一定是_________.
12.在边长为6 cm的正方形中间剪去一个边长为x cm(x<6)的小正方形,剩下的四方框形的面积为y,y与x之间的函数关系是______.
三、解答题
13.边长为4的正方形四角各剪去一个边长为的小正方形,余下的图形的面积是ycm2,求①写出与之间的函数关系式,②当x=1cm时,求的值,③如果余下的图形的面积为10,则剪去的小正方形的边长为多少?
14.正方形的边长为1 cm,假设边长增加x cm时,正方形的面积增加y cm2.
(1)请写出y与x之间的关系表达式;
(2)当正方形边长分别增加1 cm, cm,2 cm时,正方形的面积增加多少?
15.某商人如果将进价为8元的商品按每件10元出售,每天可售出100件,现在他采用提高售出价,减少进货量的办法增加利润,已知通过市场调查发现,该商品每提高1元,其销售量就要减少10件,如果他每天所赚利润为y元,试求出y和售出价x之间的函数关系式.
16.如图所示,某小区规划在一个长为40m,宽为26m的矩形场地ABCD上修建三条宽度为xm的通路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每块草坪的面积都为ym2,求y关于x的解析式.
第一课时答案
1.(1)-2,0,1(2)1,-4,3(3)4,-4,1
2.-2
3.
4.
5.C 6.C
7.
8.
9.① ②x1=1,x2=-8
10.
第二课时参考答案
一、选择题:1.C 2.D 3.C4.A 5.D 6.B
二、填空题: 7. 8. ≠±2 9. ,,
10. ,560 11. 0或3 12.
三、解答题:13. ① ② ③
14.(1) (2)3,,8
15.解:设每件商品售价为x元,则每件利润为(x-8)元,每天可售出商品[100-10(x-10)]件.所以=
16.解:有题意得种草部分总面积为
40×26-(40x+26x×2)+2x2=.
所以=.
第一课时
1.写出下列二次函数的二次项系数,一次项系数和常数项.
(1)在 中 , , ;
(2) 在中 , , ;
(3)在中 , , ;
2. 已知是关于的二次函数,则 。
3.三角形一边长为,这边上的高比的2倍少1,,则三角形的面积与之间的关系为 。
4.某厂2004年创利320万元, 如果以后每年以相同的增长率x递增, 2005年和2006年两年共创利万元,则关于的函数关系式是: .(用y=ax2+bx+c的形式表示)
5.下列函数:,,,,y=,,,其中是二次函数的有( )
A.1个 B. 2个 C. 3个 D. 4个
6.用20米长的篱笆围成一个长方形的院子,如果这个院子的面积是S米2,院子的一边长为,那么,S与的函数关系式为( )
A. B.
C. D.
7.已知:函数是二次函数,求的值并写出此函数的解析式.
8.在新年到来之际,班里每个同学都为其它同学制做了一张贺年卡,若这个班里有个同学,那么请你写出总共制作的贺年卡的张数与的函数解析式.
9.如图,矩形的长是 4cm,宽是 3cm,如果将长和宽都增加 cm,那么面积增加 ycm2,
求 y 与 x 之间的函数解析式。
求当边长增加多少时,面积增加 8cm2。
10.如图,在⊿ABC中,,动点P从点A开始沿边AC向C以2cm/s的速度移动,动点Q从点B开始沿边BC向C以4cm/s的速度移动,如果PQ分别从A、B同时出发,那么⊿PCQ的面积S随出发时间t如何变化 写出函数关系式及t的取值范围..
第二课时
一、 选择题
1.下列函数,是的二次函数的是( )
A. B. C. D.
2.函数是常数)是二次函数的条件的是( )
A. B.<0,
C.>0, D.
3. 下列函数不属二次函数的是( )
A.y=(x-1)(x+2) B.y=(x+1)2
C.y=2(x+3)2-2x2 D.y=1-x2
4.某工厂从国外进口了一套机器设备,现价值为50万元,但该套设备每年的折旧率为,那么两年之后这台机器的价值为万元,则与之间的函数关系式可以写为( )
A. B. C. D.
5.从半径是4cm的圆中挖去一个半径是xcm的圆面,剩下一个圆环的面积是ycm2,则y与x的函数关系是( )
A. B. C. D.
6.如图所示,直角三角形AOB中,AB⊥OB,且AB=OB=3,设直线,截此三角形所得的阴影部分面积是S,则S与t之间的函数关系是 ( )
A. B. C. D.
二、填空题
7.矩形的周长为80,设它们的一边长为,那么矩形的面积S与边长X之间的函数关系式为 .
8.若函数y=(k2-4)x2+(k+2)x+3是二次函数,则k______.
9.二次函数y=ax2+bx+c(a≠0)中,当b=0,c≠0时,函数表达式为______;
当b≠0, c=0时,函数表达式为______;当b=c=0时,函数表达式为______.
10.小李存入银行人民币500元,年利率为x%,两年到期,本息和为y元(不考虑利息税),y与x之间的函数关系是_______,若年利率为6%,两年到期的本利共______元.
11.如果函数是二次函数,则k得值一定是_________.
12.在边长为6 cm的正方形中间剪去一个边长为x cm(x<6)的小正方形,剩下的四方框形的面积为y,y与x之间的函数关系是______.
三、解答题
13.边长为4的正方形四角各剪去一个边长为的小正方形,余下的图形的面积是ycm2,求①写出与之间的函数关系式,②当x=1cm时,求的值,③如果余下的图形的面积为10,则剪去的小正方形的边长为多少?
14.正方形的边长为1 cm,假设边长增加x cm时,正方形的面积增加y cm2.
(1)请写出y与x之间的关系表达式;
(2)当正方形边长分别增加1 cm, cm,2 cm时,正方形的面积增加多少?
15.某商人如果将进价为8元的商品按每件10元出售,每天可售出100件,现在他采用提高售出价,减少进货量的办法增加利润,已知通过市场调查发现,该商品每提高1元,其销售量就要减少10件,如果他每天所赚利润为y元,试求出y和售出价x之间的函数关系式.
16.如图所示,某小区规划在一个长为40m,宽为26m的矩形场地ABCD上修建三条宽度为xm的通路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每块草坪的面积都为ym2,求y关于x的解析式.
第一课时答案
1.(1)-2,0,1(2)1,-4,3(3)4,-4,1
2.-2
3.
4.
5.C 6.C
7.
8.
9.① ②x1=1,x2=-8
10.
第二课时参考答案
一、选择题:1.C 2.D 3.C4.A 5.D 6.B
二、填空题: 7. 8. ≠±2 9. ,,
10. ,560 11. 0或3 12.
三、解答题:13. ① ② ③
14.(1) (2)3,,8
15.解:设每件商品售价为x元,则每件利润为(x-8)元,每天可售出商品[100-10(x-10)]件.所以=
16.解:有题意得种草部分总面积为
40×26-(40x+26x×2)+2x2=.
所以=.
