华师大版九年级数学下册试题 26.1二次函数 一课一练习题3(word版含答案)
文档属性
| 名称 | 华师大版九年级数学下册试题 26.1二次函数 一课一练习题3(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 91.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 00:00:00 | ||
图片预览

文档简介
26.1《二次函数》习题3
第一课时
一、选择
1.下列函数中属于二次函数的是( )
A. B. C. D.
2.函数y=ax2+bx+c(a,b,c是常数)是二次函数的条件是( )
A.a≠0且b≠0 B.a≠0且b≠0,c≠0
C.a≠0 D.a,b,c为任意实数
3.若是二次函数,则m的值是( )
A. B. C.或 D.
4.函数写成的形式是( )
A. B.
C. D.
5.下列哪些式子表示y是x的二次函数( )
A. B.
C. D.
6.下列函数关系中,是二次函数的是( )
A.在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.当距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长c与边长a之间的关系
D.圆心角为120°的扇形面积S与半径R之间的关系
7.某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价.若每件商品售为x元,则可卖出(350-10x)件商品,那么商品所赚钱y元与售价x元的函数关系为( )
A. B.
C. D.
二、填空题
8.圆的半径是1cm,当半径增加xcm时,圆的面积将增加ycm2,则y与x之间的函数关系为 .
9.函数y=2x2中,自变量x的取值范围是 ,函数值y的取值范围是 .
10.已知等边三角形的边长为x(cm),则此三角形的面积S(cm2)关于x的函数关系式是 .
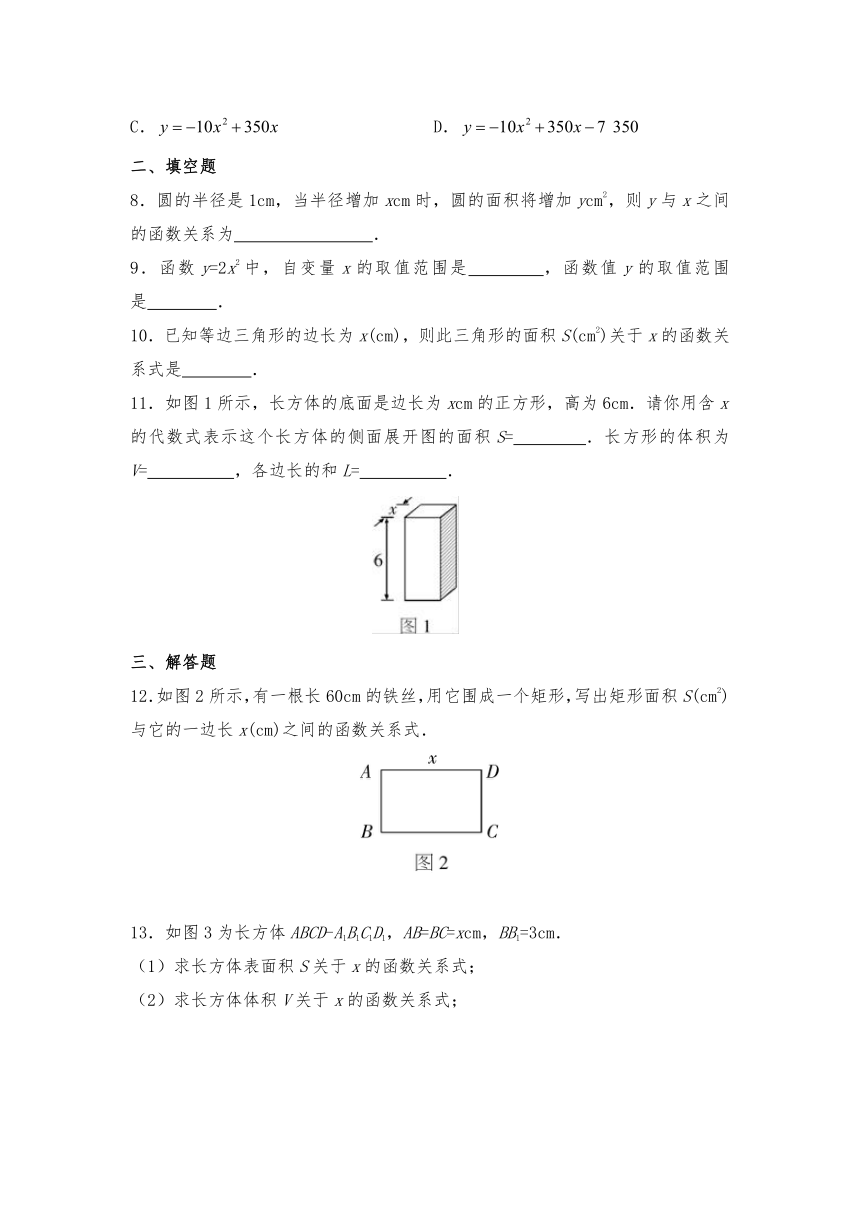
11.如图1所示,长方体的底面是边长为xcm的正方形,高为6cm.请你用含x的代数式表示这个长方体的侧面展开图的面积S= .长方形的体积为V= ,各边长的和L= .
三、解答题
12.如图2所示,有一根长60cm的铁丝,用它围成一个矩形,写出矩形面积S(cm2)与它的一边长x(cm)之间的函数关系式.
13.如图3为长方体ABCD-A1B1C1D1,AB=BC=xcm,BB1=3cm.
(1)求长方体表面积S关于x的函数关系式;
(2)求长方体体积V关于x的函数关系式;
14.某工厂前年的生产总值为10万元,去年比前年的年增长率为x,预计今年比去年的年增长率仍为x,今年的总产值为y万元.
(1)求y关于x的函数关系式.
(2)当x=20%时,今年的总产值为多少?
(3)在(2)的条件下,前年、去年和今年三年的总产值为多少万元?
第二课时
1.下列各式中,y是x的二次函数的是( )
A.x+y2-1=0 B.y=(x+1)(x-1)-x2
C.y=1+ D.2(x-1)2+3y-2=0
2.若函数y=(m2+m)是二次函数,那么m的值是( )
A.2 B.-1或3 C.3 D.-1±
3.满足函数y=x2-4x-4的一个点是( )
A.(4,4) B.(3,-1) C.(-2,-8) D.(-1,)
4.(学科内综合)写出下列各函数关系式,并判断是否是二次函数?
(1)两直角边的和为40cm,其中一条直角边长为xcm,直角三角形的面积是Scm2,写出S和x之间的函数关系式;
(2)写出圆面积S与半径r之间的函数关系式;
(3)写出正方形面积y与边长x之间的函数关系式;
(4)圆的周长c与半径r之间的函数关系式.
5.一个小球由静止开始在一个斜坡上向下滚动, 通过仪器观察到小球滚动的距离s(米)与时间t(秒)的数据如下表:
时间t(秒) 1 2 3 4 …
距离s(米) 2 8 18 32 …
写出用t表示s的函数关系式.
6.矩形窗户的周长为6m,写出窗户面积y(m2)与窗户的宽x(m) 之间的函数关系式,并判断它是否是二次函数,且求出自变量x的取值范围.
7.将一个边长为a(a为常数)的正方形, 四周剪去四个边长为x的小正方形,如图所示,则正方形剩余部分的面积为y.
请你写出y与x之间的函数关系式,并说明y与x之间是怎样的函数关系式.
第一课时参考答案
一、1~5.ACDDB 6~7.DB
二、8. 9.全体实数,大于等于0 10.
11.,,
三、12.,其中.
13.(1);
(2).
14.(1);
(2)万元;
(3)万元.
第二课时参考答案
1.D 2.C 3.D
4.解:(1)S=-x2+20x;(2)S=r2;(3)y=x2;(4)c=2r;
(1)(2)(3)是二次函数,(4)不是二次函数.
5.解:s=2t2.
6.解:y=-x2+3x,是二次函数,x的取值范围是07.解:y=a2-4x2,y是x的二次函数.
第一课时
一、选择
1.下列函数中属于二次函数的是( )
A. B. C. D.
2.函数y=ax2+bx+c(a,b,c是常数)是二次函数的条件是( )
A.a≠0且b≠0 B.a≠0且b≠0,c≠0
C.a≠0 D.a,b,c为任意实数
3.若是二次函数,则m的值是( )
A. B. C.或 D.
4.函数写成的形式是( )
A. B.
C. D.
5.下列哪些式子表示y是x的二次函数( )
A. B.
C. D.
6.下列函数关系中,是二次函数的是( )
A.在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.当距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长c与边长a之间的关系
D.圆心角为120°的扇形面积S与半径R之间的关系
7.某商店从厂家以每件21元的价格购进一批商品,该商店可以自行定价.若每件商品售为x元,则可卖出(350-10x)件商品,那么商品所赚钱y元与售价x元的函数关系为( )
A. B.
C. D.
二、填空题
8.圆的半径是1cm,当半径增加xcm时,圆的面积将增加ycm2,则y与x之间的函数关系为 .
9.函数y=2x2中,自变量x的取值范围是 ,函数值y的取值范围是 .
10.已知等边三角形的边长为x(cm),则此三角形的面积S(cm2)关于x的函数关系式是 .
11.如图1所示,长方体的底面是边长为xcm的正方形,高为6cm.请你用含x的代数式表示这个长方体的侧面展开图的面积S= .长方形的体积为V= ,各边长的和L= .
三、解答题
12.如图2所示,有一根长60cm的铁丝,用它围成一个矩形,写出矩形面积S(cm2)与它的一边长x(cm)之间的函数关系式.
13.如图3为长方体ABCD-A1B1C1D1,AB=BC=xcm,BB1=3cm.
(1)求长方体表面积S关于x的函数关系式;
(2)求长方体体积V关于x的函数关系式;
14.某工厂前年的生产总值为10万元,去年比前年的年增长率为x,预计今年比去年的年增长率仍为x,今年的总产值为y万元.
(1)求y关于x的函数关系式.
(2)当x=20%时,今年的总产值为多少?
(3)在(2)的条件下,前年、去年和今年三年的总产值为多少万元?
第二课时
1.下列各式中,y是x的二次函数的是( )
A.x+y2-1=0 B.y=(x+1)(x-1)-x2
C.y=1+ D.2(x-1)2+3y-2=0
2.若函数y=(m2+m)是二次函数,那么m的值是( )
A.2 B.-1或3 C.3 D.-1±
3.满足函数y=x2-4x-4的一个点是( )
A.(4,4) B.(3,-1) C.(-2,-8) D.(-1,)
4.(学科内综合)写出下列各函数关系式,并判断是否是二次函数?
(1)两直角边的和为40cm,其中一条直角边长为xcm,直角三角形的面积是Scm2,写出S和x之间的函数关系式;
(2)写出圆面积S与半径r之间的函数关系式;
(3)写出正方形面积y与边长x之间的函数关系式;
(4)圆的周长c与半径r之间的函数关系式.
5.一个小球由静止开始在一个斜坡上向下滚动, 通过仪器观察到小球滚动的距离s(米)与时间t(秒)的数据如下表:
时间t(秒) 1 2 3 4 …
距离s(米) 2 8 18 32 …
写出用t表示s的函数关系式.
6.矩形窗户的周长为6m,写出窗户面积y(m2)与窗户的宽x(m) 之间的函数关系式,并判断它是否是二次函数,且求出自变量x的取值范围.
7.将一个边长为a(a为常数)的正方形, 四周剪去四个边长为x的小正方形,如图所示,则正方形剩余部分的面积为y.
请你写出y与x之间的函数关系式,并说明y与x之间是怎样的函数关系式.
第一课时参考答案
一、1~5.ACDDB 6~7.DB
二、8. 9.全体实数,大于等于0 10.
11.,,
三、12.,其中.
13.(1);
(2).
14.(1);
(2)万元;
(3)万元.
第二课时参考答案
1.D 2.C 3.D
4.解:(1)S=-x2+20x;(2)S=r2;(3)y=x2;(4)c=2r;
(1)(2)(3)是二次函数,(4)不是二次函数.
5.解:s=2t2.
6.解:y=-x2+3x,是二次函数,x的取值范围是0
