1.5.2 解直角三角形在坡角(坡度)及其他方面的应用 课件(共18张PPT)
文档属性
| 名称 | 1.5.2 解直角三角形在坡角(坡度)及其他方面的应用 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 378.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 18:15:41 | ||
图片预览






文档简介
(共18张PPT)
第一章 直角三角形的边角关系
5 三角函数的应用
课时2 解直角三角形在坡角(坡度)及其他方面的应用
新课导入
直角三角形中诸元素之间的关系:
(1)三边之间的关系:a2+b2=c2 (勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
新课讲解
知识点1 用解直角三角形解坡角问题
α
A
C
B
D
E
坡面AB与水平面的夹角叫做坡角.
坡面的垂直高度与水平宽度之比叫做坡度,记作 i .
h
l
新课讲解
例
典例分析
1.如图 1-5-4,李明在大楼 30 m 高(即 PH=30 m)的窗口
P 处进行观测,测得山坡上 A 处的俯角为 15°,山脚 B处的
俯角为60° . 已知该山坡的坡度 i 为 1 ∶ ,点 P, H, B,
C, A 在同一个平面上,点 H, B, C 在同一条直线上,且
PH ⊥ HC.
(1)山坡坡角的度数等于________ 度 .
(2)求 A, B 两点间的距离(结果精确到 0.1 m,
参考数据: ≈ 1.732) .
新课讲解
将分散的条件集中到△ ABP 中求解 .
分析:
(1) 30
( 2)由题意,得∠ PBH=60°,∠ APB=60°-15°=45° .
∵∠ ABC=30°,
∴∠ ABP=90°,∴∠ BAP=45°,∴ PB=AB.
在 Rt △ PHB 中,
解:
∴ AB=PB=20 ≈ 34.6( m) .
即 A, B 两点间的距离约为 34.6 m.
新课讲解
练一练
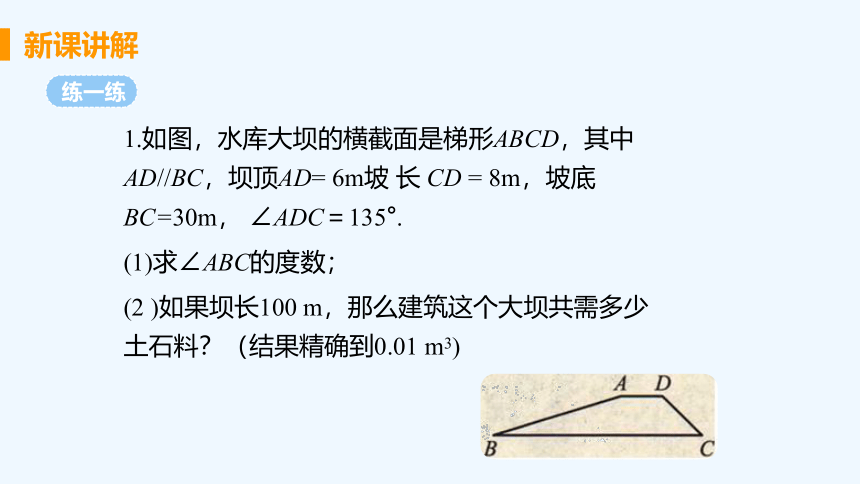
1.如图,水库大坝的横截面是梯形ABCD,其中AD//BC,坝顶AD= 6m坡 长 CD = 8m,坡底 BC=30m, ∠ADC=135°.
(1)求∠ABC的度数;
(2 )如果坝长100 m,那么建筑这个大坝共需多少土石料?(结果精确到0.01 m3)
新课讲解
(1) 过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.
∵AD∥BC,∴四边形AEFD是矩形.
∴AD=EF,AE=DF.
∵∠ADC=135°,∴∠FDC=45°.
在Rt△DCF中,DF=CDcos ∠FDC=8×cos 45°= (m),
FC=CDsin ∠FDC=8×sin 45°= (m),
∴BE=BC-EF-FC=30-6- =(24- ) m.
在Rt△ABE中,tan ∠ABE= = =
≈0.308 4,∴∠ABC≈17°8′23″.
解:
新课讲解
(2) S四边形ABCD= (AD+BC)×DF
= ×(6+30)×
= (m2),
V= ×100≈10 182.34(m3).
所以,建筑这个大坝共需约10 182.34 m3土石料.
解:
新课讲解
2.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了________米.(参考数据:sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67)
280
新课讲解
知识点2 其他应用
如图,一灯柱AB被一钢缆CD固定.CD与地面成40°夹角,且DB=5m.现再在CD上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少 (结果精确到0.01m).
钢缆问题
新课讲解
解:如图,根据题意可知,∠CDB=40°,EC=2m,DB=5m.
∴∠BDE≈51.12°.
E
B
C
D
2m
40°
5m
答:钢缆DE的长度约为7.96m.
新课讲解
如图,水库大坝的截面是梯形ABCD,坝顶AD=6m,坡长
CD=8m,坡底BC=30m,∠ADC=135°.
(1)求坡角∠ABC的大小;
(2)如果坝长100m,那么修建这个大坝共需多少土石料
(结果精确到0.01m3 )
A
B
C
D
大坝问题
新课讲解
(1)解:如图,过点D作DE⊥BC于点E,
过点A作AF⊥BC于点F.
A
B
C
D
6m
8m
30m
135°
E
┐
F
┌
∴∠ABC≈17°8′21″.
答:坡角∠ABC约为17°8′21″.
新课讲解
(2)解:如图,
答:修建这个大坝共需土石方约10182.34m3.
100m
A
B
C
D
6m
30m
F
┌
课堂小结
实际问题
图形分析
生活问题数学化
(构造直角三角形)
设未知量
解答问题
(构建三角函数模型)
(代入数据求解)
求解方程
数学问题
建立方程
当堂小练
1.为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD. 已知迎水坡面AB=12米,背水坡面CD=123米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tan E= ,则CE的长为_______.
8m
当堂小练
2.如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
A.5.1米
B.6.3米
C.7.1米
D.9.2米
A
拓展与延伸
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3 米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
A.5米
B.6米
C.8米
D.(3+ )米
A
第一章 直角三角形的边角关系
5 三角函数的应用
课时2 解直角三角形在坡角(坡度)及其他方面的应用
新课导入
直角三角形中诸元素之间的关系:
(1)三边之间的关系:a2+b2=c2 (勾股定理);
(2)锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
新课讲解
知识点1 用解直角三角形解坡角问题
α
A
C
B
D
E
坡面AB与水平面的夹角叫做坡角.
坡面的垂直高度与水平宽度之比叫做坡度,记作 i .
h
l
新课讲解
例
典例分析
1.如图 1-5-4,李明在大楼 30 m 高(即 PH=30 m)的窗口
P 处进行观测,测得山坡上 A 处的俯角为 15°,山脚 B处的
俯角为60° . 已知该山坡的坡度 i 为 1 ∶ ,点 P, H, B,
C, A 在同一个平面上,点 H, B, C 在同一条直线上,且
PH ⊥ HC.
(1)山坡坡角的度数等于________ 度 .
(2)求 A, B 两点间的距离(结果精确到 0.1 m,
参考数据: ≈ 1.732) .
新课讲解
将分散的条件集中到△ ABP 中求解 .
分析:
(1) 30
( 2)由题意,得∠ PBH=60°,∠ APB=60°-15°=45° .
∵∠ ABC=30°,
∴∠ ABP=90°,∴∠ BAP=45°,∴ PB=AB.
在 Rt △ PHB 中,
解:
∴ AB=PB=20 ≈ 34.6( m) .
即 A, B 两点间的距离约为 34.6 m.
新课讲解
练一练
1.如图,水库大坝的横截面是梯形ABCD,其中AD//BC,坝顶AD= 6m坡 长 CD = 8m,坡底 BC=30m, ∠ADC=135°.
(1)求∠ABC的度数;
(2 )如果坝长100 m,那么建筑这个大坝共需多少土石料?(结果精确到0.01 m3)
新课讲解
(1) 过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.
∵AD∥BC,∴四边形AEFD是矩形.
∴AD=EF,AE=DF.
∵∠ADC=135°,∴∠FDC=45°.
在Rt△DCF中,DF=CDcos ∠FDC=8×cos 45°= (m),
FC=CDsin ∠FDC=8×sin 45°= (m),
∴BE=BC-EF-FC=30-6- =(24- ) m.
在Rt△ABE中,tan ∠ABE= = =
≈0.308 4,∴∠ABC≈17°8′23″.
解:
新课讲解
(2) S四边形ABCD= (AD+BC)×DF
= ×(6+30)×
= (m2),
V= ×100≈10 182.34(m3).
所以,建筑这个大坝共需约10 182.34 m3土石料.
解:
新课讲解
2.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了________米.(参考数据:sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67)
280
新课讲解
知识点2 其他应用
如图,一灯柱AB被一钢缆CD固定.CD与地面成40°夹角,且DB=5m.现再在CD上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少 (结果精确到0.01m).
钢缆问题
新课讲解
解:如图,根据题意可知,∠CDB=40°,EC=2m,DB=5m.
∴∠BDE≈51.12°.
E
B
C
D
2m
40°
5m
答:钢缆DE的长度约为7.96m.
新课讲解
如图,水库大坝的截面是梯形ABCD,坝顶AD=6m,坡长
CD=8m,坡底BC=30m,∠ADC=135°.
(1)求坡角∠ABC的大小;
(2)如果坝长100m,那么修建这个大坝共需多少土石料
(结果精确到0.01m3 )
A
B
C
D
大坝问题
新课讲解
(1)解:如图,过点D作DE⊥BC于点E,
过点A作AF⊥BC于点F.
A
B
C
D
6m
8m
30m
135°
E
┐
F
┌
∴∠ABC≈17°8′21″.
答:坡角∠ABC约为17°8′21″.
新课讲解
(2)解:如图,
答:修建这个大坝共需土石方约10182.34m3.
100m
A
B
C
D
6m
30m
F
┌
课堂小结
实际问题
图形分析
生活问题数学化
(构造直角三角形)
设未知量
解答问题
(构建三角函数模型)
(代入数据求解)
求解方程
数学问题
建立方程
当堂小练
1.为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD. 已知迎水坡面AB=12米,背水坡面CD=123米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tan E= ,则CE的长为_______.
8m
当堂小练
2.如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
A.5.1米
B.6.3米
C.7.1米
D.9.2米
A
拓展与延伸
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3 米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
A.5米
B.6米
C.8米
D.(3+ )米
A
