1.6利用三角函数测高 课件(共20张PPT)
文档属性
| 名称 | 1.6利用三角函数测高 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 463.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 18:30:55 | ||
图片预览



文档简介
(共14张PPT)
第一章 直角三角形的边角关系
6 利用三角函数测高
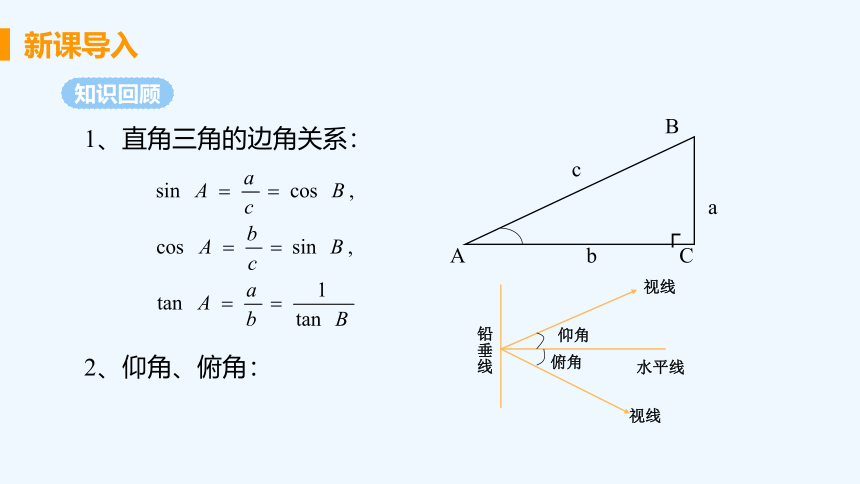
新课导入
知识回顾
1、直角三角的边角关系:
b
A
B
C
a
┌
c
2、仰角、俯角:
铅垂线
仰角
俯角
水平线
视线
视线
新课导入
情境导入
根据我们所学的数学知识,你能测出他们的高度吗?
新课讲解
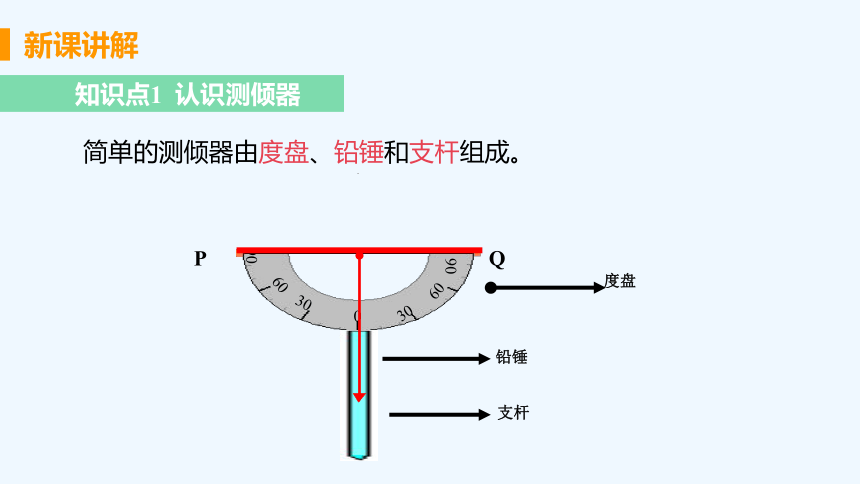
知识点1 认识测倾器
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
简单的测倾器由度盘、铅锤和支杆组成。
新课讲解
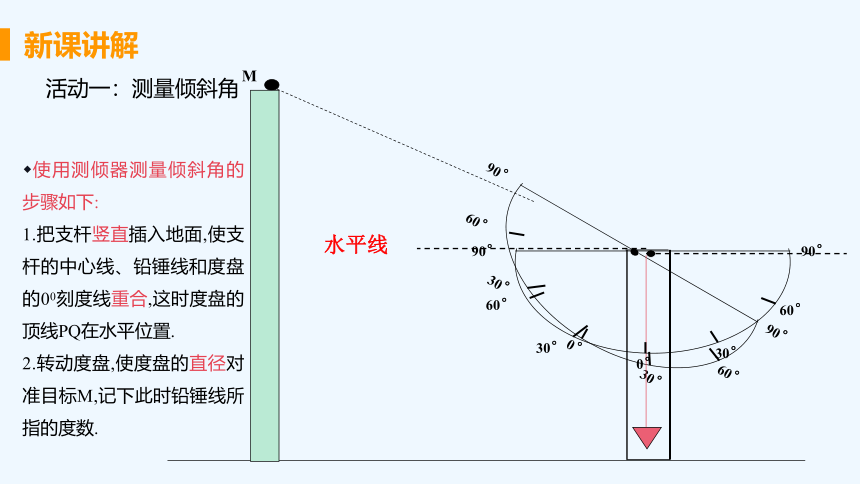
活动一:测量倾斜角
30°
0°
60°
90°
90°
60°
30°
30°
0°
60°
90°
90°
60°
30°
水平线
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线、铅锤线和度盘的00刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅锤线所指的度数.
M
新课讲解
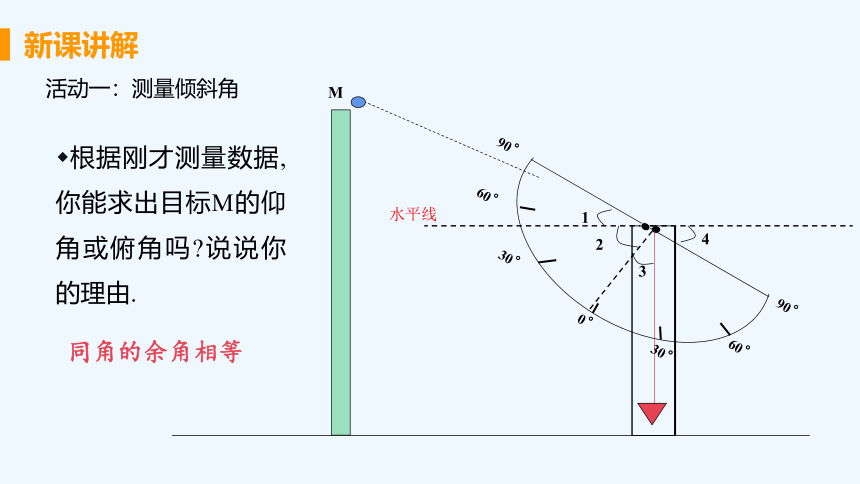
活动一:测量倾斜角
根据刚才测量数据,你能求出目标M的仰角或俯角吗 说说你的理由.
1
2
3
4
30°
0°
60°
90°
90°
60°
30°
水平线
M
同角的余角相等
新课讲解
活动二:测量底部可以到达的物体的高度
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体底部之间的距离.
如图,要测量物体MN的高度,需测量哪些数据?
1.在测点A处安置测倾器,
测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=L.
3.量出测倾器的高度AC=a
C
A
E
N
M
a
L
α
可按下列步骤进行:
新课讲解
a
C
A
E
N
M
L
α
根据刚才测量的数据,你能求出物体MN的高度吗 说说你的理由.
在Rt△MCE中,
ME=EC tanα=AN tanα
=L tanα
MN=ME+EN=ME+AC=L tanα+ a
新课讲解
活动三:测量底部不可以到达的物体的高度
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体底部之间的距离.(如图)
要测量物体MN的高度,使用侧倾器测一次仰角够吗?为什么?
a
α
E
C
A
N
M
新课讲解
a
b
α
E
C
A
D
B
β
N
M
如图,要测量物体MN的高度,可以按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾(A,B与N在一条直线上),测得M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
根据测量数据,你能求出物体MN的高度吗 说说你的理由.
新课讲解
根据测量数据,物体MN的高度计算过程:
a
b
α
E
C
A
D
B
β
N
M
在Rt△MDE中,
ED=
在Rt△MCE中,
EC =
EC-ED= - =b
课堂小结
利用三角函数测高
全等法
三角函数法
相似法
侧倾器
测量两种情形下物体高度
测量物体高度的方法
当堂小练
如图,在高20米的建筑物CD的顶部C测得塔顶A的仰角为60° ,测得塔底B的俯角为30°,则塔高AB = 米;
80
拓展与延伸
如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着倾角为30°的山坡前进1 000米到达D处,在D处测得山顶B的仰角为60°,则山高BC大约是(精确到0.1米)( )
1 366.0米 B. 1 482.1米
C. 1 295.9米 D. 1 508.2米
A
第一章 直角三角形的边角关系
6 利用三角函数测高
新课导入
知识回顾
1、直角三角的边角关系:
b
A
B
C
a
┌
c
2、仰角、俯角:
铅垂线
仰角
俯角
水平线
视线
视线
新课导入
情境导入
根据我们所学的数学知识,你能测出他们的高度吗?
新课讲解
知识点1 认识测倾器
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
简单的测倾器由度盘、铅锤和支杆组成。
新课讲解
活动一:测量倾斜角
30°
0°
60°
90°
90°
60°
30°
30°
0°
60°
90°
90°
60°
30°
水平线
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线、铅锤线和度盘的00刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅锤线所指的度数.
M
新课讲解
活动一:测量倾斜角
根据刚才测量数据,你能求出目标M的仰角或俯角吗 说说你的理由.
1
2
3
4
30°
0°
60°
90°
90°
60°
30°
水平线
M
同角的余角相等
新课讲解
活动二:测量底部可以到达的物体的高度
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体底部之间的距离.
如图,要测量物体MN的高度,需测量哪些数据?
1.在测点A处安置测倾器,
测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=L.
3.量出测倾器的高度AC=a
C
A
E
N
M
a
L
α
可按下列步骤进行:
新课讲解
a
C
A
E
N
M
L
α
根据刚才测量的数据,你能求出物体MN的高度吗 说说你的理由.
在Rt△MCE中,
ME=EC tanα=AN tanα
=L tanα
MN=ME+EN=ME+AC=L tanα+ a
新课讲解
活动三:测量底部不可以到达的物体的高度
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体底部之间的距离.(如图)
要测量物体MN的高度,使用侧倾器测一次仰角够吗?为什么?
a
α
E
C
A
N
M
新课讲解
a
b
α
E
C
A
D
B
β
N
M
如图,要测量物体MN的高度,可以按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾(A,B与N在一条直线上),测得M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
根据测量数据,你能求出物体MN的高度吗 说说你的理由.
新课讲解
根据测量数据,物体MN的高度计算过程:
a
b
α
E
C
A
D
B
β
N
M
在Rt△MDE中,
ED=
在Rt△MCE中,
EC =
EC-ED= - =b
课堂小结
利用三角函数测高
全等法
三角函数法
相似法
侧倾器
测量两种情形下物体高度
测量物体高度的方法
当堂小练
如图,在高20米的建筑物CD的顶部C测得塔顶A的仰角为60° ,测得塔底B的俯角为30°,则塔高AB = 米;
80
拓展与延伸
如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着倾角为30°的山坡前进1 000米到达D处,在D处测得山顶B的仰角为60°,则山高BC大约是(精确到0.1米)( )
1 366.0米 B. 1 482.1米
C. 1 295.9米 D. 1 508.2米
A
