2021-2022学年人教版八年级数学下册第16章二次根式周末自主提升训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册第16章二次根式周末自主提升训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 138.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 00:00:00 | ||
图片预览



文档简介
2021-2022学年人教版八年级数学下册《第16章二次根式》周末自主提升训练(附答案)
一.选择题
1.下列各式中,一定是二次根式的是( )
A. B. C. D.
2.若代数式有意义的m的取值范围为( )
A.m≥2 B.m≤2 C.m<2 D.m>2
3.若a<0,则化简|a﹣3|﹣的结果为( )
A.3﹣2a B.3 C.﹣3 D.2a﹣3
4.在实数范围内要使=a﹣2成立,则a的取值范围是( )
A.a=2 B.a>2 C.a≥2 D.a≤2
5.当a<0时,化简a 的结果是( )
A.﹣4a B.4a C.﹣4a2 D.4a2
6.实数a,b在数轴上的位置如图所示,化简的结果是( )
A.﹣a+b B.﹣a﹣b C.a+b D.a﹣b
7.若最简二次根式与最简二次根式是可以合并的二次根式,则a的值是( )
A.a=1 B.a=﹣1 C.a=2 D.a=﹣2
8.下列计算结果正确的有( )
①a5÷a=a5;②=﹣x4y4;③;④(a﹣3)﹣2=a6;⑤a0=1;⑥.
A.2个 B.3个 C.4个 D.5个
二.填空题
9.若是二次根式,则a的取值范围是 ;若是正整数,则正整数a的最小值是 .
10.已知y=+x﹣2,则= .
11.实数a在数轴上的位置如图所示,化简:|a﹣2|+= .
12.下列各式:
(1);(2);(3);(4);(5);(6);(7)中,
是最简二次根式的是 (填序号).
13.计算:= .
三.解答题
14.计算:
(1)+|1﹣|﹣4+6÷2;
(2)(3+)(3﹣)﹣(1﹣)2.
15.计算:
(1)(2﹣)(3+2);
(2)(+﹣)(﹣+).
16.已知x=+,y=﹣,求:
(1)+的值;
(2)2x2+6xy+2y2的值.
17.已知x=.
(1)求代数式x+;
(2)求(7﹣4)x2+(2﹣)x+的值.
18.如图,在△ABC中,CD、CE分别是AB上的高和中线,S△ABC=12cm2,AE=2cm,求CD的长.
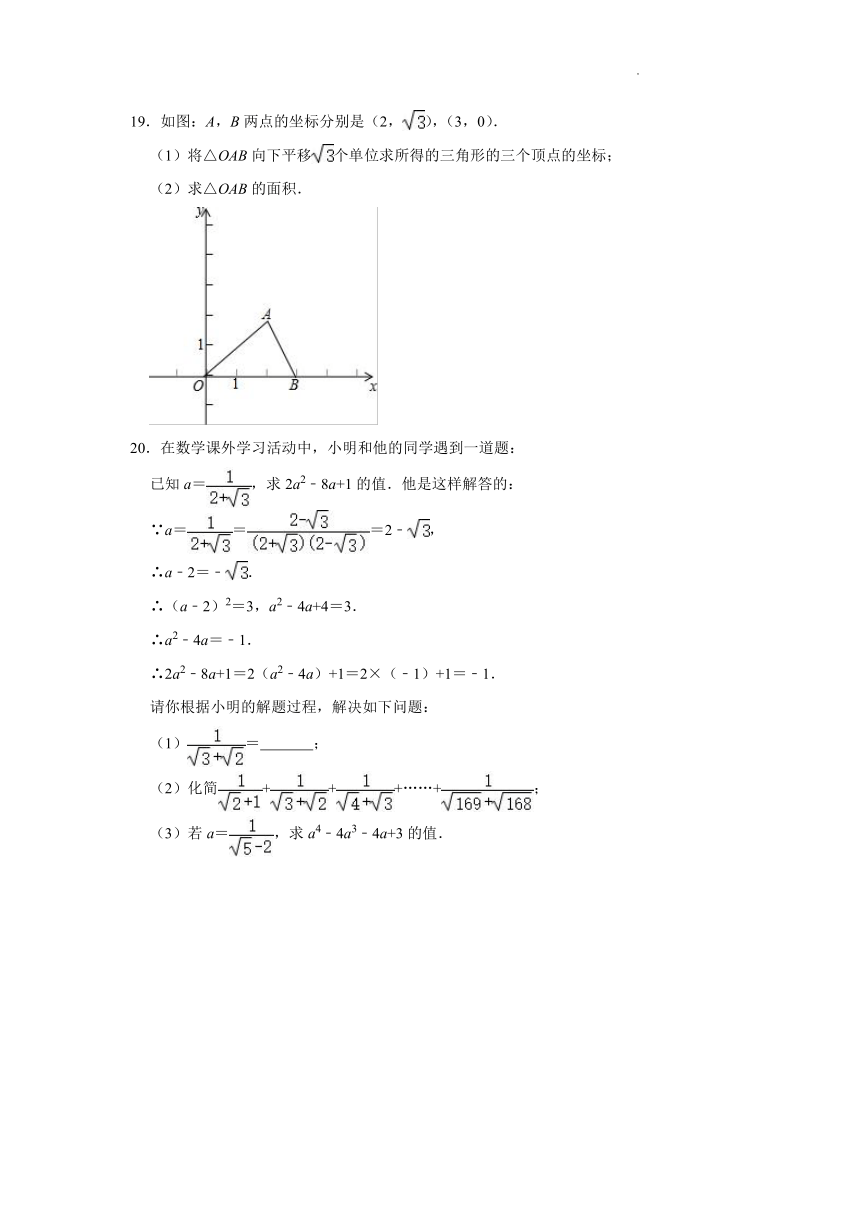
19.如图:A,B两点的坐标分别是(2,),(3,0).
(1)将△OAB向下平移个单位求所得的三角形的三个顶点的坐标;
(2)求△OAB的面积.
20.在数学课外学习活动中,小明和他的同学遇到一道题:
已知a=,求2a2﹣8a+1的值.他是这样解答的:
∵a===2﹣,
∴a﹣2=﹣.
∴(a﹣2)2=3,a2﹣4a+4=3.
∴a2﹣4a=﹣1.
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的解题过程,解决如下问题:
(1)= ;
(2)化简+++……+;
(3)若a=,求a4﹣4a3﹣4a+3的值.
参考答案
一.选择题
1.解:A、当a+1<0时,不是二次根式,故此选项不符合题意;
B、当a﹣1<0时,不是二次根式,故此选项不符合题意;
C、当a=0时,a2﹣1=﹣1<0,不是二次根式,故此选项不符合题意;
D、∵a2≥0,∴a2+2>0,是二次根式,故此选项符合题意;
故选:D.
2.解:由题意可知:>0,
∴m>2,
故选:D.
3.解:∵a<0,
∴a﹣3<0,
∴|a﹣3|﹣
=3﹣a﹣(﹣a)
=3﹣a+a
=3,
故选:B.
4.解:原式=|a﹣2|=a﹣2,
∴a﹣2≥0,
解得:a≥2,
故选:C.
5.解:∵当a<0时,
∴a
=a
=a (﹣4a)
=﹣4a2.
故选:C.
6.解:由题意得:
b<0<a,
∴
=a+(﹣b)
=a﹣b,
故选:D.
7.解:由题意可知:a+1=2a
解得:a=1
故选:A.
8.解:①a5÷a=a4,故此选项不合题意;
②=x4y4,故此选项不合题意;
③+无法合并,故此选项不合题意;
④(a﹣3)﹣2=a6,故此选项符合题意;
⑤a0=1(a≠0),故此选项不合题意;
⑥,故此选项符合题意.
故选:A.
二.填空题
9.解:∵是二次根式,
∴300a≥0,
∴a≥0,
∴若是二次根式,则a的取值范围是:a≥0,
∵=10,
∴若是正整数,则正整数a的最小值是3,
故答案为:a≥0,3.
10.解:∵x﹣1≥0,1﹣x≥0,
∴x=1,
∴y=﹣1,
∴原式===3.
故答案为:3.
11.解:由数轴可知:a﹣2<0,a﹣1>0,
原式=|a﹣2|+
=|a﹣2|+|a﹣1|
=﹣(a﹣2)+(a﹣1)
=﹣a+2+a﹣1
=1,
故答案为:1.
12.解:(2),(3),
故答案为:②,③.
13.解:原式=,
=,
=,
=2,
故答案为:2.
三.解答题
14.解:(1)原式=3+﹣1﹣4×+3
=3+﹣1﹣2+6
=2+5;
(2)原式=()2﹣()2﹣(1﹣2+5)
=18﹣3﹣6+2
=9+2.
15.解:(1)(2﹣)(3+2)
=6+4﹣3﹣4
=2+;
(2)(+﹣)(﹣+)
=[+()][﹣()]
=2﹣()2
=2﹣3+2﹣5
=﹣6+2.
16.解:(1)∵x=+,y=﹣,
∴x+y=2,
xy=1,
∴+
=
=
=
=10;
(2)∵x=+,y=﹣,
∴2x2+6xy+2y2
=2x2+4xy+2y2+2xy
=2(x+y)2+2xy
=2(++﹣)2+2×(+)×(﹣)
=24+2
=26.
17.解:(1)x===2+,
则=2﹣,
∴x+=2++2﹣=4;
(2)(7﹣4)x2+(2﹣)x+
=(7﹣4)(2+)2+(2﹣)(2+)+
=(7﹣4)(7+4)+(2﹣)(2+)+
=49﹣48+4﹣3+
=2+.
18.解:在△ABC中,CE是AB上的中线,S△ABC=12cm2,
∴S△AEC=S△ABC=6cm2,
∵AE=2cm,
∴AE CD=6,即×2 CD=6,
∴CD=6.
19.解:(1)
∴所得的三角形的三个顶点的坐标为A′(2,0),O′(0,﹣),B′(3,﹣)
△OAB的面积=×3×=.
20.解:(1)==﹣;
故答案为﹣;
(2)原式=﹣1+﹣+﹣+…+﹣
=﹣1
=13﹣1
=12;
(3)∵a==+2,
∴a﹣2=,
∴(a﹣2)2=5,即a2﹣4a+4=5.
∴a2﹣4a=1.
∴a4﹣4a3﹣4a+3=a2(a2﹣4a)﹣4a+3
=a2×1﹣4a+3
=a2﹣4a+3
=1+3=4.
一.选择题
1.下列各式中,一定是二次根式的是( )
A. B. C. D.
2.若代数式有意义的m的取值范围为( )
A.m≥2 B.m≤2 C.m<2 D.m>2
3.若a<0,则化简|a﹣3|﹣的结果为( )
A.3﹣2a B.3 C.﹣3 D.2a﹣3
4.在实数范围内要使=a﹣2成立,则a的取值范围是( )
A.a=2 B.a>2 C.a≥2 D.a≤2
5.当a<0时,化简a 的结果是( )
A.﹣4a B.4a C.﹣4a2 D.4a2
6.实数a,b在数轴上的位置如图所示,化简的结果是( )
A.﹣a+b B.﹣a﹣b C.a+b D.a﹣b
7.若最简二次根式与最简二次根式是可以合并的二次根式,则a的值是( )
A.a=1 B.a=﹣1 C.a=2 D.a=﹣2
8.下列计算结果正确的有( )
①a5÷a=a5;②=﹣x4y4;③;④(a﹣3)﹣2=a6;⑤a0=1;⑥.
A.2个 B.3个 C.4个 D.5个
二.填空题
9.若是二次根式,则a的取值范围是 ;若是正整数,则正整数a的最小值是 .
10.已知y=+x﹣2,则= .
11.实数a在数轴上的位置如图所示,化简:|a﹣2|+= .
12.下列各式:
(1);(2);(3);(4);(5);(6);(7)中,
是最简二次根式的是 (填序号).
13.计算:= .
三.解答题
14.计算:
(1)+|1﹣|﹣4+6÷2;
(2)(3+)(3﹣)﹣(1﹣)2.
15.计算:
(1)(2﹣)(3+2);
(2)(+﹣)(﹣+).
16.已知x=+,y=﹣,求:
(1)+的值;
(2)2x2+6xy+2y2的值.
17.已知x=.
(1)求代数式x+;
(2)求(7﹣4)x2+(2﹣)x+的值.
18.如图,在△ABC中,CD、CE分别是AB上的高和中线,S△ABC=12cm2,AE=2cm,求CD的长.
19.如图:A,B两点的坐标分别是(2,),(3,0).
(1)将△OAB向下平移个单位求所得的三角形的三个顶点的坐标;
(2)求△OAB的面积.
20.在数学课外学习活动中,小明和他的同学遇到一道题:
已知a=,求2a2﹣8a+1的值.他是这样解答的:
∵a===2﹣,
∴a﹣2=﹣.
∴(a﹣2)2=3,a2﹣4a+4=3.
∴a2﹣4a=﹣1.
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的解题过程,解决如下问题:
(1)= ;
(2)化简+++……+;
(3)若a=,求a4﹣4a3﹣4a+3的值.
参考答案
一.选择题
1.解:A、当a+1<0时,不是二次根式,故此选项不符合题意;
B、当a﹣1<0时,不是二次根式,故此选项不符合题意;
C、当a=0时,a2﹣1=﹣1<0,不是二次根式,故此选项不符合题意;
D、∵a2≥0,∴a2+2>0,是二次根式,故此选项符合题意;
故选:D.
2.解:由题意可知:>0,
∴m>2,
故选:D.
3.解:∵a<0,
∴a﹣3<0,
∴|a﹣3|﹣
=3﹣a﹣(﹣a)
=3﹣a+a
=3,
故选:B.
4.解:原式=|a﹣2|=a﹣2,
∴a﹣2≥0,
解得:a≥2,
故选:C.
5.解:∵当a<0时,
∴a
=a
=a (﹣4a)
=﹣4a2.
故选:C.
6.解:由题意得:
b<0<a,
∴
=a+(﹣b)
=a﹣b,
故选:D.
7.解:由题意可知:a+1=2a
解得:a=1
故选:A.
8.解:①a5÷a=a4,故此选项不合题意;
②=x4y4,故此选项不合题意;
③+无法合并,故此选项不合题意;
④(a﹣3)﹣2=a6,故此选项符合题意;
⑤a0=1(a≠0),故此选项不合题意;
⑥,故此选项符合题意.
故选:A.
二.填空题
9.解:∵是二次根式,
∴300a≥0,
∴a≥0,
∴若是二次根式,则a的取值范围是:a≥0,
∵=10,
∴若是正整数,则正整数a的最小值是3,
故答案为:a≥0,3.
10.解:∵x﹣1≥0,1﹣x≥0,
∴x=1,
∴y=﹣1,
∴原式===3.
故答案为:3.
11.解:由数轴可知:a﹣2<0,a﹣1>0,
原式=|a﹣2|+
=|a﹣2|+|a﹣1|
=﹣(a﹣2)+(a﹣1)
=﹣a+2+a﹣1
=1,
故答案为:1.
12.解:(2),(3),
故答案为:②,③.
13.解:原式=,
=,
=,
=2,
故答案为:2.
三.解答题
14.解:(1)原式=3+﹣1﹣4×+3
=3+﹣1﹣2+6
=2+5;
(2)原式=()2﹣()2﹣(1﹣2+5)
=18﹣3﹣6+2
=9+2.
15.解:(1)(2﹣)(3+2)
=6+4﹣3﹣4
=2+;
(2)(+﹣)(﹣+)
=[+()][﹣()]
=2﹣()2
=2﹣3+2﹣5
=﹣6+2.
16.解:(1)∵x=+,y=﹣,
∴x+y=2,
xy=1,
∴+
=
=
=
=10;
(2)∵x=+,y=﹣,
∴2x2+6xy+2y2
=2x2+4xy+2y2+2xy
=2(x+y)2+2xy
=2(++﹣)2+2×(+)×(﹣)
=24+2
=26.
17.解:(1)x===2+,
则=2﹣,
∴x+=2++2﹣=4;
(2)(7﹣4)x2+(2﹣)x+
=(7﹣4)(2+)2+(2﹣)(2+)+
=(7﹣4)(7+4)+(2﹣)(2+)+
=49﹣48+4﹣3+
=2+.
18.解:在△ABC中,CE是AB上的中线,S△ABC=12cm2,
∴S△AEC=S△ABC=6cm2,
∵AE=2cm,
∴AE CD=6,即×2 CD=6,
∴CD=6.
19.解:(1)
∴所得的三角形的三个顶点的坐标为A′(2,0),O′(0,﹣),B′(3,﹣)
△OAB的面积=×3×=.
20.解:(1)==﹣;
故答案为﹣;
(2)原式=﹣1+﹣+﹣+…+﹣
=﹣1
=13﹣1
=12;
(3)∵a==+2,
∴a﹣2=,
∴(a﹣2)2=5,即a2﹣4a+4=5.
∴a2﹣4a=1.
∴a4﹣4a3﹣4a+3=a2(a2﹣4a)﹣4a+3
=a2×1﹣4a+3
=a2﹣4a+3
=1+3=4.
