苏科版七年级数学下册 7.2 探索平行线的性质 教案
文档属性
| 名称 | 苏科版七年级数学下册 7.2 探索平行线的性质 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 112.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 00:00:00 | ||
图片预览

文档简介
7.2《平行线的判定和性质》(复习课)
教学目标
知识与技能:
1、理解并掌握平行线常用的三个判定方法,能正确找出条件证明直线的平行。
2、理解掌握平行线的三个性质,能用平行线的性质去解决一些问题。
过程与方法:经过复习概念、小组抢答竞争、合作讨论、师生互动、生生互动等学习过程,让学生感受回忆、观察、讨论、归纳、小结等学习方法。
情感态度与价值观:
培养学生数形结合数学思想
培养学生的合作意识和互助意识
教学重点:平行线的判定和性质综合运用。
教学难点:平行线的判定及其性质的灵活应用,书写格式。
教学方法 自主探究 合作交流
教学过程设计
一、复习提问:①平行线的判定方法有哪些?
②平行线的性质有哪些?
二、 平行线的判定与性质的区别与联系
1、区别:判定是:根据角 或角 ,去证 .
性质是:根据两直线平行,去证角 或角
2、联系:它们都是以两条平行直线被第三条直线所截为前提;
它们的条件和结论是 的。
3、总结:已知平行用 ,要证平行用
三、应用
(环节一)限时答题,小组大比拼
题组一:
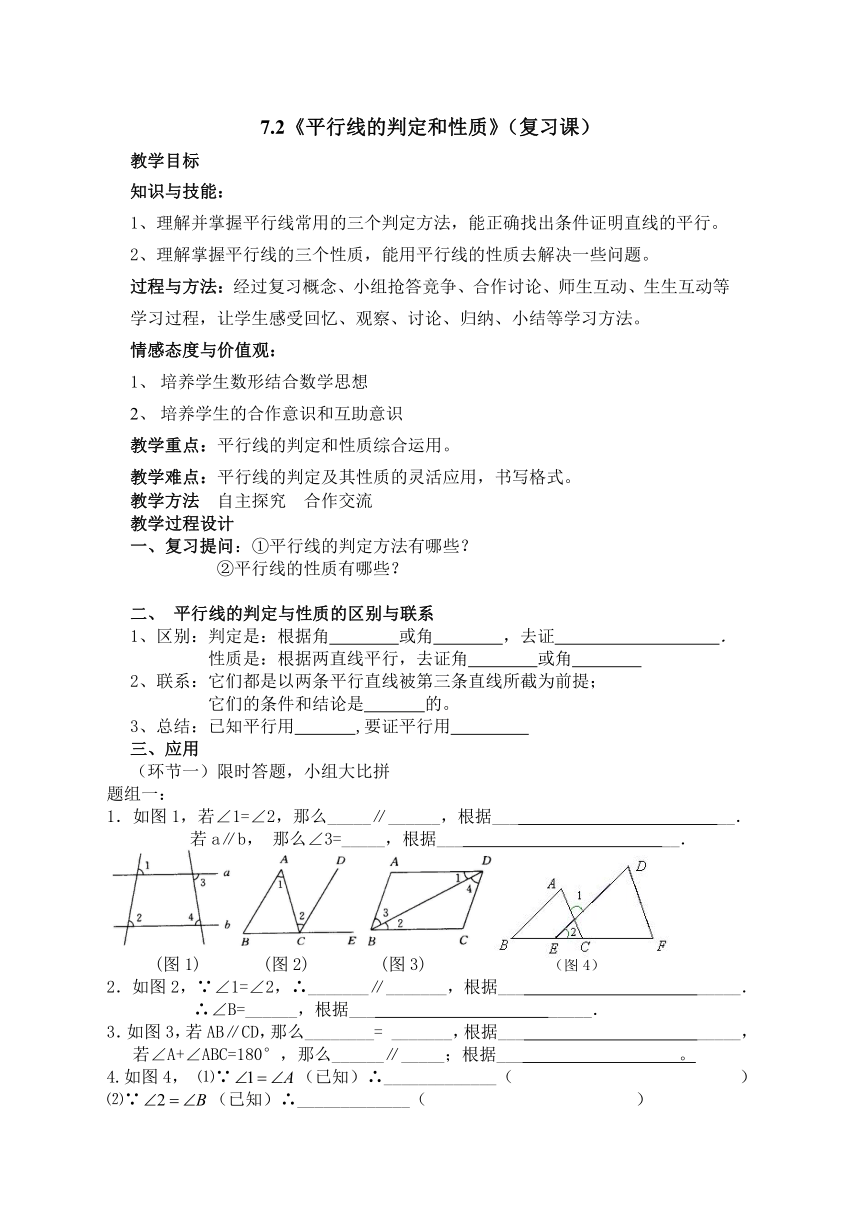
1.如图1,若∠1=∠2,那么_____∥______,根据___ __.
若a∥b,那么∠3=_____,根据___ __.
(图1) (图2) (图3) (图4)
2.如图2,∵∠1=∠2,∴_______∥_______,根据___ _____.
∴∠B=______,根据___ _____.
3.如图3,若AB∥CD,那么________=_______,根据___ _____,
若∠A+∠ABC=180°,那么______∥_____;根据___ 。
4.如图4, ⑴∵(已知)∴_____________( )
⑵∵(已知)∴_____________( )
题组二:
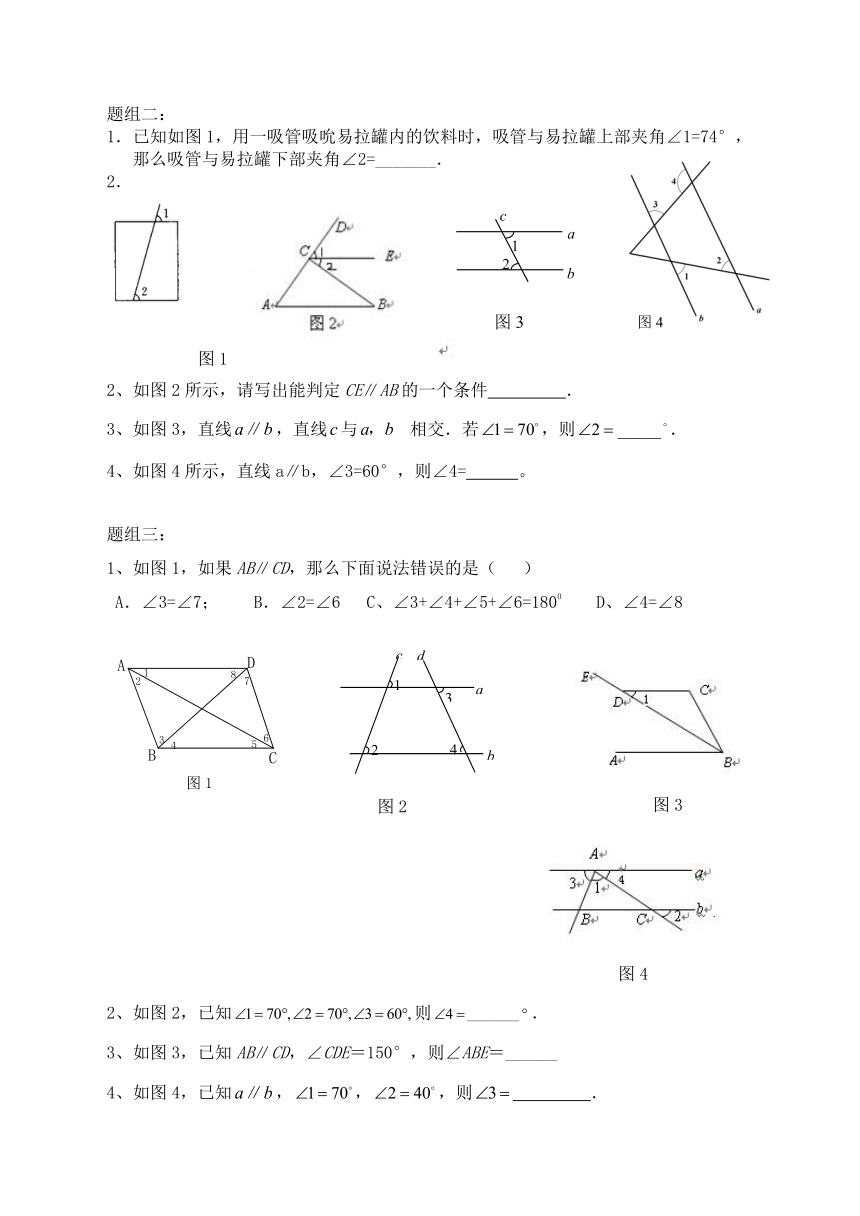
已知如图1,用一吸管吸吮易拉罐内的饮料时,吸管与易拉罐上部夹角∠1=74°,那么吸管与易拉罐下部夹角∠2=_______.
(
图
4
) (
图
3
) (
1
2
b
a
c
)图1
2、如图2所示,请写出能判定CE∥AB的一个条件 .
3、如图3,直线,直线与 相交.若,则.
4、如图4所示,直线a∥b,∠3=60°,则∠4= 。
题组三:
1、如图1,如果AB∥CD,那么下面说法错误的是( )
A.∠3=∠7; B.∠2=∠6 C、∠3+∠4+∠5+∠6=1800 D、∠4=∠8
(
b
a
c
d
1
2
3
4
) (
图
1
)
(
图
2
) 图3
图4
2、如图2,已知则______.
3、如图3,已知AB∥CD,∠CDE=150°,则∠ABE=______
4、如图4,已知,,,则 .
(环节二)例题讲解,形成能力
例 如图:AB∥CD,∠B=28°,∠D=32°,则∠BED的度数是多少度?
变式1:如图所示,已知AB∥CD,∠ABE=130°,∠CDE=152°,求∠BED的度数.
变式2:如图,已知,∠B=120°,∠C等于25°,求的度数。
(
O
)
(环节三)合作解疑,看谁最棒
1、如图,已知:AB ∥CD,MG平分∠AMN ,NH平分∠DNM,求证:MG∥NH。
2、如图,已知AD⊥BC于D,EF⊥BC于F,∠E=∠1,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由。
(
_
C
_
B
_
D
_
E
_
F
_
A
_
)
(环节四)课时小结:
1、平行线的判定和性质
2、平行线的判定和性质的区别和联系
3、已知平行用性质,要证平行用判定
作业布置:《同步》
教学目标
知识与技能:
1、理解并掌握平行线常用的三个判定方法,能正确找出条件证明直线的平行。
2、理解掌握平行线的三个性质,能用平行线的性质去解决一些问题。
过程与方法:经过复习概念、小组抢答竞争、合作讨论、师生互动、生生互动等学习过程,让学生感受回忆、观察、讨论、归纳、小结等学习方法。
情感态度与价值观:
培养学生数形结合数学思想
培养学生的合作意识和互助意识
教学重点:平行线的判定和性质综合运用。
教学难点:平行线的判定及其性质的灵活应用,书写格式。
教学方法 自主探究 合作交流
教学过程设计
一、复习提问:①平行线的判定方法有哪些?
②平行线的性质有哪些?
二、 平行线的判定与性质的区别与联系
1、区别:判定是:根据角 或角 ,去证 .
性质是:根据两直线平行,去证角 或角
2、联系:它们都是以两条平行直线被第三条直线所截为前提;
它们的条件和结论是 的。
3、总结:已知平行用 ,要证平行用
三、应用
(环节一)限时答题,小组大比拼
题组一:
1.如图1,若∠1=∠2,那么_____∥______,根据___ __.
若a∥b,那么∠3=_____,根据___ __.
(图1) (图2) (图3) (图4)
2.如图2,∵∠1=∠2,∴_______∥_______,根据___ _____.
∴∠B=______,根据___ _____.
3.如图3,若AB∥CD,那么________=_______,根据___ _____,
若∠A+∠ABC=180°,那么______∥_____;根据___ 。
4.如图4, ⑴∵(已知)∴_____________( )
⑵∵(已知)∴_____________( )
题组二:
已知如图1,用一吸管吸吮易拉罐内的饮料时,吸管与易拉罐上部夹角∠1=74°,那么吸管与易拉罐下部夹角∠2=_______.
(
图
4
) (
图
3
) (
1
2
b
a
c
)图1
2、如图2所示,请写出能判定CE∥AB的一个条件 .
3、如图3,直线,直线与 相交.若,则.
4、如图4所示,直线a∥b,∠3=60°,则∠4= 。
题组三:
1、如图1,如果AB∥CD,那么下面说法错误的是( )
A.∠3=∠7; B.∠2=∠6 C、∠3+∠4+∠5+∠6=1800 D、∠4=∠8
(
b
a
c
d
1
2
3
4
) (
图
1
)
(
图
2
) 图3
图4
2、如图2,已知则______.
3、如图3,已知AB∥CD,∠CDE=150°,则∠ABE=______
4、如图4,已知,,,则 .
(环节二)例题讲解,形成能力
例 如图:AB∥CD,∠B=28°,∠D=32°,则∠BED的度数是多少度?
变式1:如图所示,已知AB∥CD,∠ABE=130°,∠CDE=152°,求∠BED的度数.
变式2:如图,已知,∠B=120°,∠C等于25°,求的度数。
(
O
)
(环节三)合作解疑,看谁最棒
1、如图,已知:AB ∥CD,MG平分∠AMN ,NH平分∠DNM,求证:MG∥NH。
2、如图,已知AD⊥BC于D,EF⊥BC于F,∠E=∠1,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由。
(
_
C
_
B
_
D
_
E
_
F
_
A
_
)
(环节四)课时小结:
1、平行线的判定和性质
2、平行线的判定和性质的区别和联系
3、已知平行用性质,要证平行用判定
作业布置:《同步》
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
