北师大版七年级数学下册 4.3 等腰三角形的轴对称性 课件(共21张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 4.3 等腰三角形的轴对称性 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-19 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
等腰三角形
—“瘦身” 复习课
等腰三角形
—“瘦身” 复习课
等腰三角形
—“瘦身” 复习课
小组长汇报预习案完成情况:
等腰三角形 — 热身运动
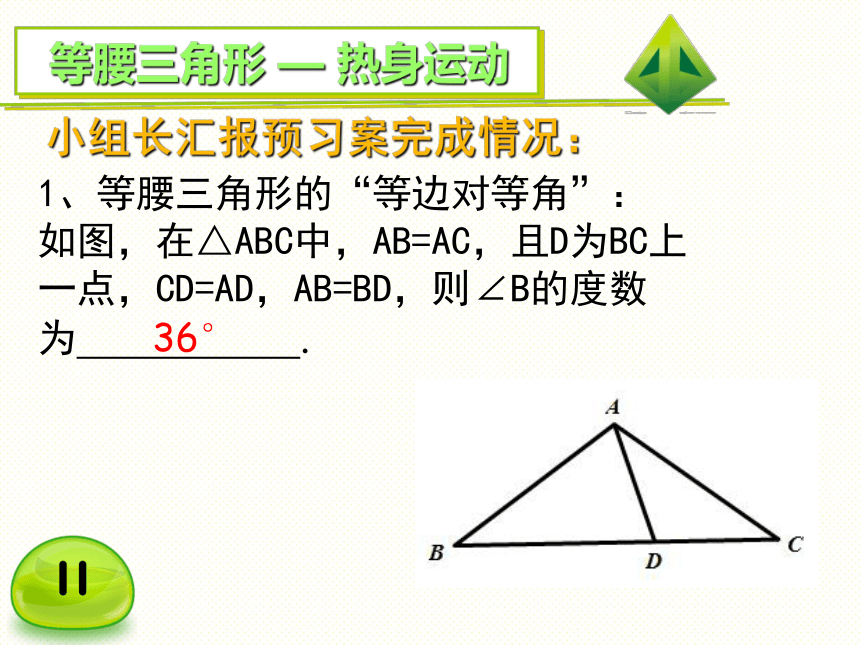
1、等腰三角形的“等边对等角”:
如图,在△ABC中,AB=AC,且D为BC上
一点,CD=AD,AB=BD,则∠B的度数
为 .
36°
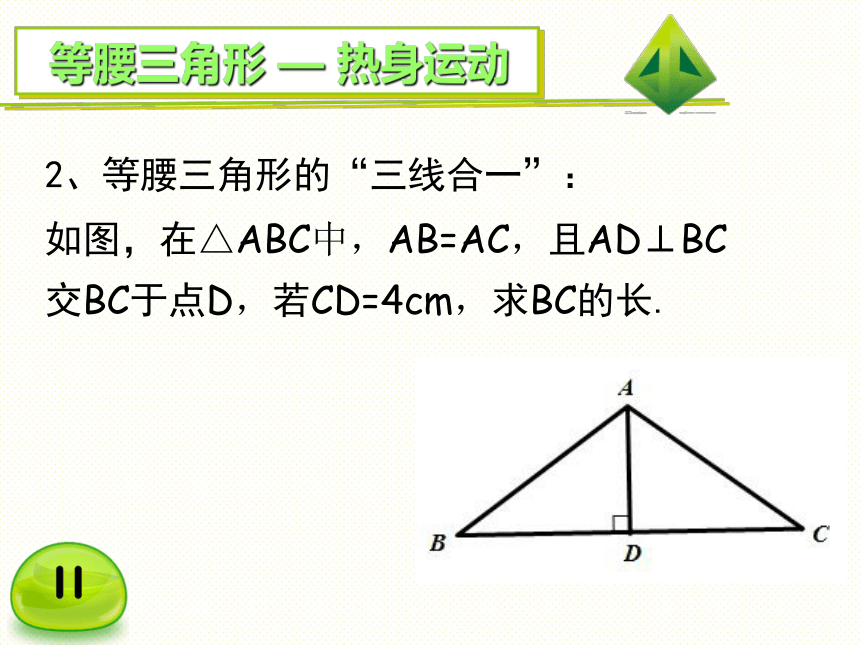
2、等腰三角形的“三线合一”:
如图,在△ABC中,AB=AC,且AD⊥BC交BC于点D,若CD=4cm,求BC的长.
等腰三角形 — 热身运动
等腰三角形 — 热身运动
注 意:
“三线合一”的性质为证明角相等,线段相等及线段垂直提供有力工具.
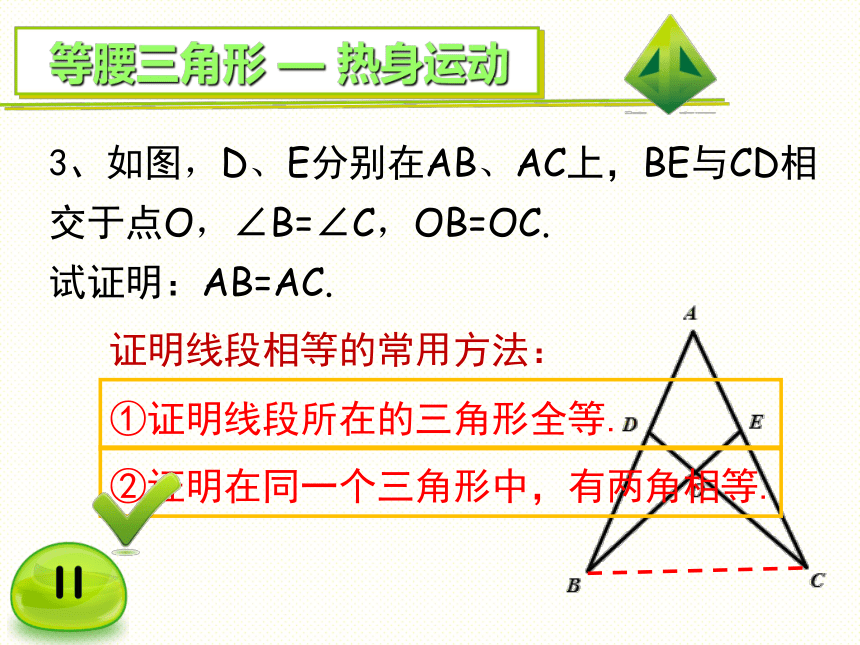
3、如图,D、E分别在AB、AC上,BE与CD相交于点O,∠B=∠C,OB=OC.
试证明:AB=AC.
等腰三角形 — 热身运动
①证明线段所在的三角形全等.
证明线段相等的常用方法:
②证明在同一个三角形中,有两角相等.
1
2
3
熟练掌握等腰三角形的性质和判定,并能灵活运用.
利用等腰三角形的性质,巧作辅助线.
通过解题方法对比、反思,更好的体验和感悟等腰三角形的对称性,方程、转化、最优化和分类讨论等数学思想.
学习目标
探 究 一
01
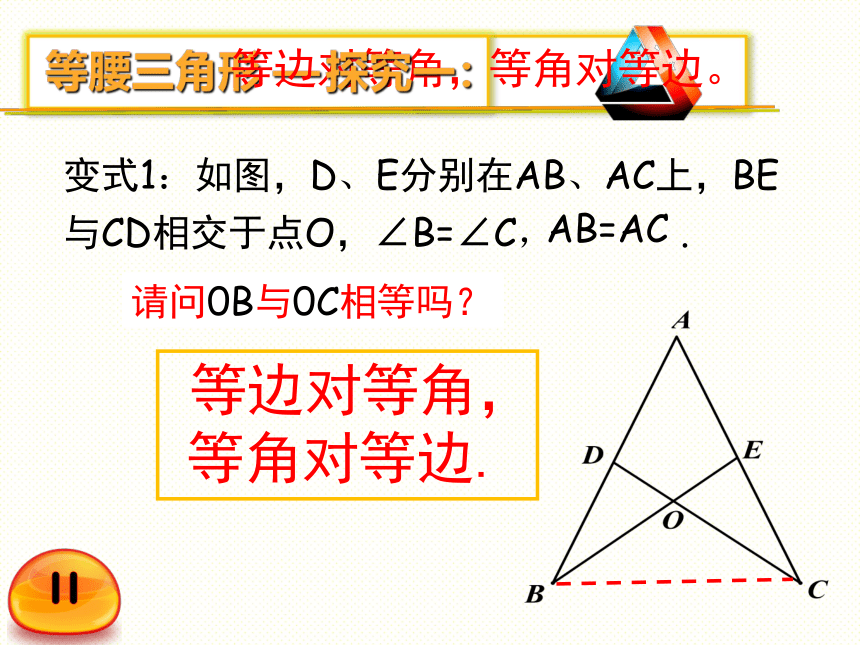
变式1:如图,D、E分别在AB、AC上,BE与CD相交于点O,∠B=∠C, .
等腰三角形 —
AB=AC
请问0B与0C相等吗?
等边对等角, 等角对等边.
等边对等角,等角对等边。
探究一:
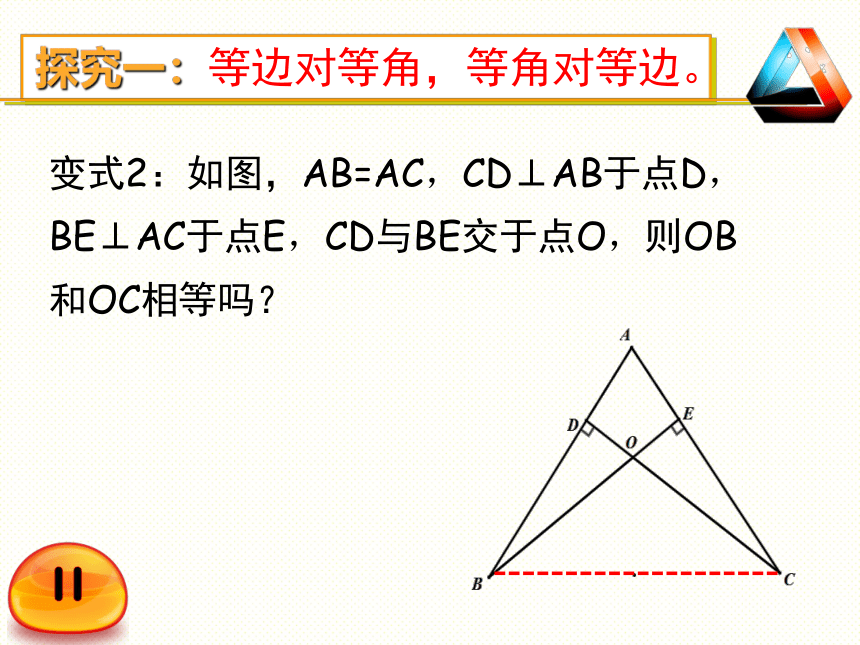
变式2:如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD与BE交于点O,则OB和OC相等吗?
探究一:等边对等角,等角对等边。
变式3:如图,AB=AC,CD⊥AB交AB的
延长线于点D,BE⊥AC交AC的延长线于点E.
延长BE,CD交于点O, 则OB,OC还能相等吗?
. . .
. . .
探究一:等边对等角,等角对等边。
O
如图,AB=DC,∠A=∠D,则∠B=∠C吗?
等腰三角形 —合作探究
O
构造三角形
O
O
探 究 二
02
如图,点B、D、E、C在同一条直线上, AB=AC,AD=AE,那么BD与CE有怎样的数量关系?请说明理由.
探究二:“三线合一”
┐
F
∠D=∠E
变式 .如图,BD=CE,∠B=∠C, ,
F是DE的中点.则AF与DE有怎样的位置关系?
请说明理由.
1
2
AB=AC
探究二:“三线合一”
G
H
利用“三线合一”
构造基本图形
┐
F
G
H
厚积薄发
03
等腰三角形 — 合作交流
如图, AB∥CD,E是AD的中点,分别连接BE、CE.当BE与CE满足什么位置关系时,点E是∠BCD与∠ABC平分线的交点,试说明理由.
分别延长BE,CD交于点F
F
等腰三角形 — 感悟与收获
通过本节课的学习,你最大的感悟和收获是什么?请和大家分享一下!
2.挑课堂精炼至少2道典型习题,将全等过程“瘦身”.
1.自编一道试题,解题过程体现运用等腰三角形性质的优越性.
大庆一中
姜晓莺
等腰三角形 — 创新作业
谢谢您的聆听!
等腰三角形
—“瘦身” 复习课
等腰三角形
—“瘦身” 复习课
等腰三角形
—“瘦身” 复习课
小组长汇报预习案完成情况:
等腰三角形 — 热身运动
1、等腰三角形的“等边对等角”:
如图,在△ABC中,AB=AC,且D为BC上
一点,CD=AD,AB=BD,则∠B的度数
为 .
36°
2、等腰三角形的“三线合一”:
如图,在△ABC中,AB=AC,且AD⊥BC交BC于点D,若CD=4cm,求BC的长.
等腰三角形 — 热身运动
等腰三角形 — 热身运动
注 意:
“三线合一”的性质为证明角相等,线段相等及线段垂直提供有力工具.
3、如图,D、E分别在AB、AC上,BE与CD相交于点O,∠B=∠C,OB=OC.
试证明:AB=AC.
等腰三角形 — 热身运动
①证明线段所在的三角形全等.
证明线段相等的常用方法:
②证明在同一个三角形中,有两角相等.
1
2
3
熟练掌握等腰三角形的性质和判定,并能灵活运用.
利用等腰三角形的性质,巧作辅助线.
通过解题方法对比、反思,更好的体验和感悟等腰三角形的对称性,方程、转化、最优化和分类讨论等数学思想.
学习目标
探 究 一
01
变式1:如图,D、E分别在AB、AC上,BE与CD相交于点O,∠B=∠C, .
等腰三角形 —
AB=AC
请问0B与0C相等吗?
等边对等角, 等角对等边.
等边对等角,等角对等边。
探究一:
变式2:如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD与BE交于点O,则OB和OC相等吗?
探究一:等边对等角,等角对等边。
变式3:如图,AB=AC,CD⊥AB交AB的
延长线于点D,BE⊥AC交AC的延长线于点E.
延长BE,CD交于点O, 则OB,OC还能相等吗?
. . .
. . .
探究一:等边对等角,等角对等边。
O
如图,AB=DC,∠A=∠D,则∠B=∠C吗?
等腰三角形 —合作探究
O
构造三角形
O
O
探 究 二
02
如图,点B、D、E、C在同一条直线上, AB=AC,AD=AE,那么BD与CE有怎样的数量关系?请说明理由.
探究二:“三线合一”
┐
F
∠D=∠E
变式 .如图,BD=CE,∠B=∠C, ,
F是DE的中点.则AF与DE有怎样的位置关系?
请说明理由.
1
2
AB=AC
探究二:“三线合一”
G
H
利用“三线合一”
构造基本图形
┐
F
G
H
厚积薄发
03
等腰三角形 — 合作交流
如图, AB∥CD,E是AD的中点,分别连接BE、CE.当BE与CE满足什么位置关系时,点E是∠BCD与∠ABC平分线的交点,试说明理由.
分别延长BE,CD交于点F
F
等腰三角形 — 感悟与收获
通过本节课的学习,你最大的感悟和收获是什么?请和大家分享一下!
2.挑课堂精炼至少2道典型习题,将全等过程“瘦身”.
1.自编一道试题,解题过程体现运用等腰三角形性质的优越性.
大庆一中
姜晓莺
等腰三角形 — 创新作业
谢谢您的聆听!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
